13.1.1 轴对称 课件(共23张PPT)
文档属性
| 名称 | 13.1.1 轴对称 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-07 08:24:56 | ||
图片预览








文档简介
(共23张PPT)
人教版 八年级数学上
13.1.1轴对称
学习目标
1.通过实例了解轴对称图形和两个图形成轴对称的概念,掌握两者之间的区别和联系,并能准确识别.
2.掌握轴对称图形和两个图形成轴对称的性质,体会类比方法在数学问题中的应用.
课题导入
对称现象无处不在,从自然景观到艺术作品,从建筑物到交通标
志,甚至日常生活用品中,人们都可以找到对称的例子!
合作探究
思考:如图,把一张纸对折,剪出一个图案(折痕处不要完全剪断),再打开这张对折的纸,就得到了美丽的窗花.观察得到的窗花,你能发现它们有什么共同的特点吗?
合作探究
像上图一样,如果一个平面图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形,这条直线就是它的对称轴.这时,我们也说这个图形关于这条直线(成轴)对称.
你能举出一些轴对称的例子吗?
对称轴
合作探究
思考:下面的每对图形有什么共同特点?
A
B
C
对称轴
对称轴
把一个图形沿一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线(成轴)对称,这条直线就是它的对称轴.
A′
B′
C′
对称点
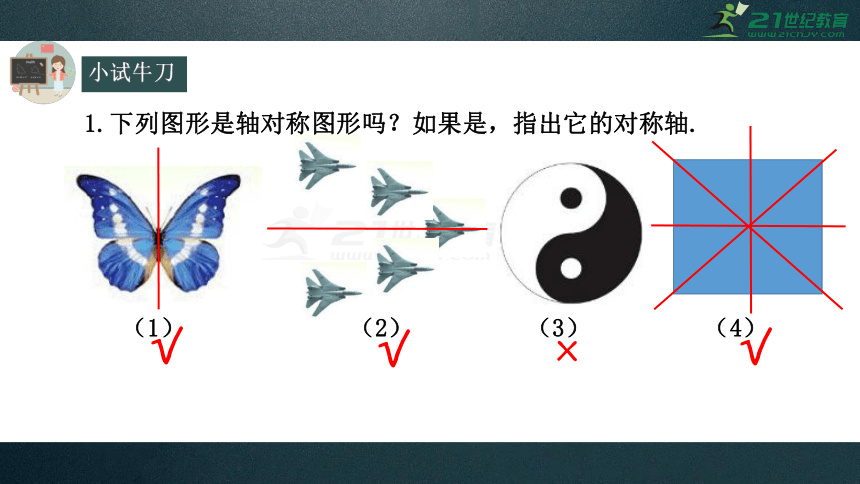
小试牛刀
1.下列图形是轴对称图形吗?如果是,指出它的对称轴.
(1) (2) (3) (4)
√
√
×
√
小试牛刀
2.如图所示的每幅图形中的两个图案是轴对称的吗?如果是,指出它们的对称轴,并找出一对对称点.
(1) (2) (3)
√
√
×
合作探究
思考:成轴对称的两个图形全等吗?如果把一个轴对称图形沿对称轴分成两个图形,那么这两个图形全等吗?这两个图形对称吗?
把成轴对称的两个图形看成一个整体,它就是一个轴对称图形.
把一个轴对称图形分成两个图形,这两个图形关于这条轴对称.
合作探究
轴对称图形 两个图形成轴对称
图形
区别
联系
一个图形具有的特殊形状
两个全等图形的特殊的位置关系
1.都是沿着某条直线折叠后能重合.
2.可以互相转化.
比一比
合作探究
思考:如图,△ABC和△A′B′C′关于直线MN对称,点A′,B′,C′分别是点A,B,C的对称点,线段AA′,BB′,CC′与直线MN有什么关系?
A
B
C
A′
B′
C′
N
M
AA′⊥MN,
BB′⊥MN,
CC′⊥MN.
PA=PA′
QB=QB′
HC=HC′
P
Q
H
对称轴经过对称点所连线段的中点,并且垂直这条线段。
垂直平分线
合作探究
如图,MN⊥AA′,AP=A′P.
直线MN是线段AA′的垂直平分线.
如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.
★线段垂直平分线的定义
经过线段中点并且垂直于这条线段的直线.
★图形轴对称的性质:
M
P
Q
H
A
B
C
A′
B′
C′
合作探究
类似地,轴对称图形的对称轴,是任何一对对称点所连线段的垂直平分线.
轴对称图形的性质:
A
B
A′
B′
M
N
如图,MN垂直平分AA ′, MN垂直平分BB ′.
小试牛刀
1.下列图形中,△A′B′C′与△ABC关于直线MN成轴对称的是( )
B
小试牛刀
2.如图,△ABC与△DEF关于直线MN轴对称,则以下结论中不正确
的是( )
A.AB∥DF
B.∠C=∠F
C.AC=DF
D.点B、E的连线被MN垂直平分
A
实战演练
1.下图中,是否是轴对称图形?若是,则分别指出它们的对称轴.
①
②
③
④
⑤
√
√
√
×
√
实战演练
2.下图中,左边图形和右边图形成轴对称的有( ).
A.1组 B.2组 C.3组 D.4组
C
①
②
③
实战演练
4.如图,Rt△ABC中,∠ABC=90°,∠C=60°,将其折叠,使点A落在边AB上C′处,折痕为
BD,则∠C′DA的度数为_______.
30°
3.下图是由“○”和“□”组成的轴对称图形,
该图形的对称轴是直线( )
A. a B.b C.c D.d
C
○
○
○
○
○
□
□
□
c
b
a
d
A
C′
D
C
B
实战演练
5.如图,正方形ABCD的边长为6cm,则图中阴影部分
的面积为( )
A.6cm2 B.18cm2 C.12cm2 D.16cm2
B
6.如图,OE平分∠AOB,BD⊥OA,AC⊥OB,AC、
BD相交于点E,则关于直线OE对称的三角形有
对.
3
D
E
B
O
A
C
实战演练
7.下列说法:
①.两个全等图形一定是轴对称,
②.关于某条直线对称的两个图形一定是全等形,
③.轴对称图形中对称点所连线段垂直平分对称轴,
④.轴对称图形中的对称点必须在对称轴两侧,
⑤.轴对称图形中的对称点在对称轴上,则这点与它的对称点重合.
其中正确的是 .
②、⑤
课堂总结
今天我们收获了哪些知识?(畅所欲言)
1.说一说轴对称图形和两个图形成轴对称的区别与联系?
2.什么是线段的垂直平分线?
3.成轴对称的两个图形有什么性质?
课后作业
教材64页习题13.1第2、3、4、5题.
https://www.21cnjy.com/help/help_extract.php
人教版 八年级数学上
13.1.1轴对称
学习目标
1.通过实例了解轴对称图形和两个图形成轴对称的概念,掌握两者之间的区别和联系,并能准确识别.
2.掌握轴对称图形和两个图形成轴对称的性质,体会类比方法在数学问题中的应用.
课题导入
对称现象无处不在,从自然景观到艺术作品,从建筑物到交通标
志,甚至日常生活用品中,人们都可以找到对称的例子!
合作探究
思考:如图,把一张纸对折,剪出一个图案(折痕处不要完全剪断),再打开这张对折的纸,就得到了美丽的窗花.观察得到的窗花,你能发现它们有什么共同的特点吗?
合作探究
像上图一样,如果一个平面图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形,这条直线就是它的对称轴.这时,我们也说这个图形关于这条直线(成轴)对称.
你能举出一些轴对称的例子吗?
对称轴
合作探究
思考:下面的每对图形有什么共同特点?
A
B
C
对称轴
对称轴
把一个图形沿一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线(成轴)对称,这条直线就是它的对称轴.
A′
B′
C′
对称点
小试牛刀
1.下列图形是轴对称图形吗?如果是,指出它的对称轴.
(1) (2) (3) (4)
√
√
×
√
小试牛刀
2.如图所示的每幅图形中的两个图案是轴对称的吗?如果是,指出它们的对称轴,并找出一对对称点.
(1) (2) (3)
√
√
×
合作探究
思考:成轴对称的两个图形全等吗?如果把一个轴对称图形沿对称轴分成两个图形,那么这两个图形全等吗?这两个图形对称吗?
把成轴对称的两个图形看成一个整体,它就是一个轴对称图形.
把一个轴对称图形分成两个图形,这两个图形关于这条轴对称.
合作探究
轴对称图形 两个图形成轴对称
图形
区别
联系
一个图形具有的特殊形状
两个全等图形的特殊的位置关系
1.都是沿着某条直线折叠后能重合.
2.可以互相转化.
比一比
合作探究
思考:如图,△ABC和△A′B′C′关于直线MN对称,点A′,B′,C′分别是点A,B,C的对称点,线段AA′,BB′,CC′与直线MN有什么关系?
A
B
C
A′
B′
C′
N
M
AA′⊥MN,
BB′⊥MN,
CC′⊥MN.
PA=PA′
QB=QB′
HC=HC′
P
Q
H
对称轴经过对称点所连线段的中点,并且垂直这条线段。
垂直平分线
合作探究
如图,MN⊥AA′,AP=A′P.
直线MN是线段AA′的垂直平分线.
如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.
★线段垂直平分线的定义
经过线段中点并且垂直于这条线段的直线.
★图形轴对称的性质:
M
P
Q
H
A
B
C
A′
B′
C′
合作探究
类似地,轴对称图形的对称轴,是任何一对对称点所连线段的垂直平分线.
轴对称图形的性质:
A
B
A′
B′
M
N
如图,MN垂直平分AA ′, MN垂直平分BB ′.
小试牛刀
1.下列图形中,△A′B′C′与△ABC关于直线MN成轴对称的是( )
B
小试牛刀
2.如图,△ABC与△DEF关于直线MN轴对称,则以下结论中不正确
的是( )
A.AB∥DF
B.∠C=∠F
C.AC=DF
D.点B、E的连线被MN垂直平分
A
实战演练
1.下图中,是否是轴对称图形?若是,则分别指出它们的对称轴.
①
②
③
④
⑤
√
√
√
×
√
实战演练
2.下图中,左边图形和右边图形成轴对称的有( ).
A.1组 B.2组 C.3组 D.4组
C
①
②
③
实战演练
4.如图,Rt△ABC中,∠ABC=90°,∠C=60°,将其折叠,使点A落在边AB上C′处,折痕为
BD,则∠C′DA的度数为_______.
30°
3.下图是由“○”和“□”组成的轴对称图形,
该图形的对称轴是直线( )
A. a B.b C.c D.d
C
○
○
○
○
○
□
□
□
c
b
a
d
A
C′
D
C
B
实战演练
5.如图,正方形ABCD的边长为6cm,则图中阴影部分
的面积为( )
A.6cm2 B.18cm2 C.12cm2 D.16cm2
B
6.如图,OE平分∠AOB,BD⊥OA,AC⊥OB,AC、
BD相交于点E,则关于直线OE对称的三角形有
对.
3
D
E
B
O
A
C
实战演练
7.下列说法:
①.两个全等图形一定是轴对称,
②.关于某条直线对称的两个图形一定是全等形,
③.轴对称图形中对称点所连线段垂直平分对称轴,
④.轴对称图形中的对称点必须在对称轴两侧,
⑤.轴对称图形中的对称点在对称轴上,则这点与它的对称点重合.
其中正确的是 .
②、⑤
课堂总结
今天我们收获了哪些知识?(畅所欲言)
1.说一说轴对称图形和两个图形成轴对称的区别与联系?
2.什么是线段的垂直平分线?
3.成轴对称的两个图形有什么性质?
课后作业
教材64页习题13.1第2、3、4、5题.
https://www.21cnjy.com/help/help_extract.php
