2015-2016学年湘教版九年级数学下期末检测题及答案解析
文档属性
| 名称 | 2015-2016学年湘教版九年级数学下期末检测题及答案解析 |  | |
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-01-06 16:42:43 | ||
图片预览


文档简介
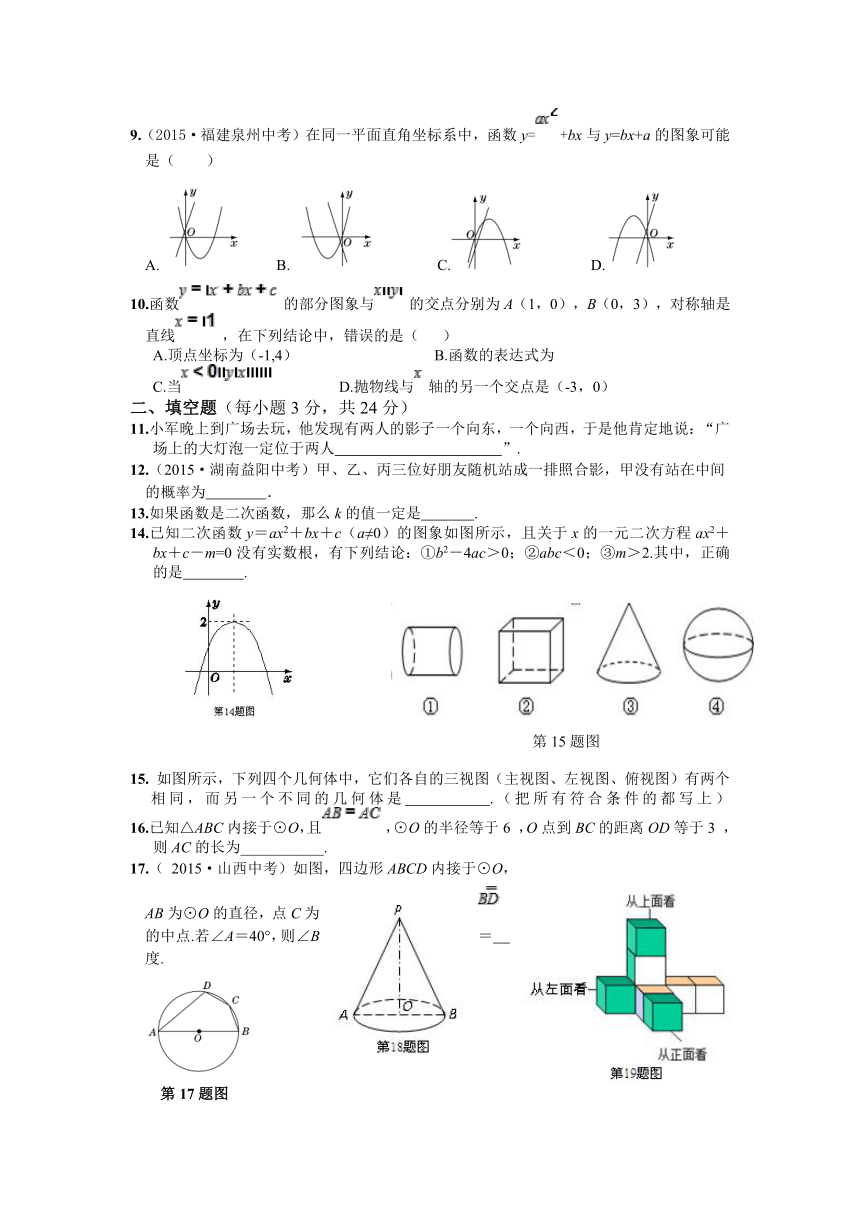
期末检测题
(本检测题满分:120分,时间:120分钟)
一、选择题(每小题3分,共30分)
1.抛物线y=的对称轴是( )
A.y轴 B.直线x=-1 C.直线x=1 D.直线x=-3
2.(2015·湖南益阳中考)一个几何体的三视图如图所示,则这个几何体是( )
A.三棱锥 B.三棱柱 C.圆柱 D.长方体
3.如图,AB是⊙O的直径,BC,CD,DA是⊙O的弦,且,则∠( )
A.100° B.110° C.120° D.135°
4.如图,一把遮阳伞撑开时母线的长是2 m,底面半径为1 m,则做这把遮阳伞需用布料的面积是( )
A. m B. m
C. m D. m
5.如图,圆O的直径AB垂直于弦CD,垂足是E,∠A=22.5°,OC=4,CD 的长为( )
A. B.4
C. D.8
6.两个不同长度的物体在同一时刻同一地点的太阳光下得到的投影长
度的关系是 ( )
A.相等 B.长的较长 C.短的较长 D.不能确定
7.如图,△ABC的三个顶点都在⊙O上,∠BAC的平分线交BC于点D,交⊙O于点E,则与△ABD相似的三角形有( )
A.3个 B.2个 C.1个 D.0个
8.如图,已知的半径,,则所对的弧的长为( )
A. B. C. D.
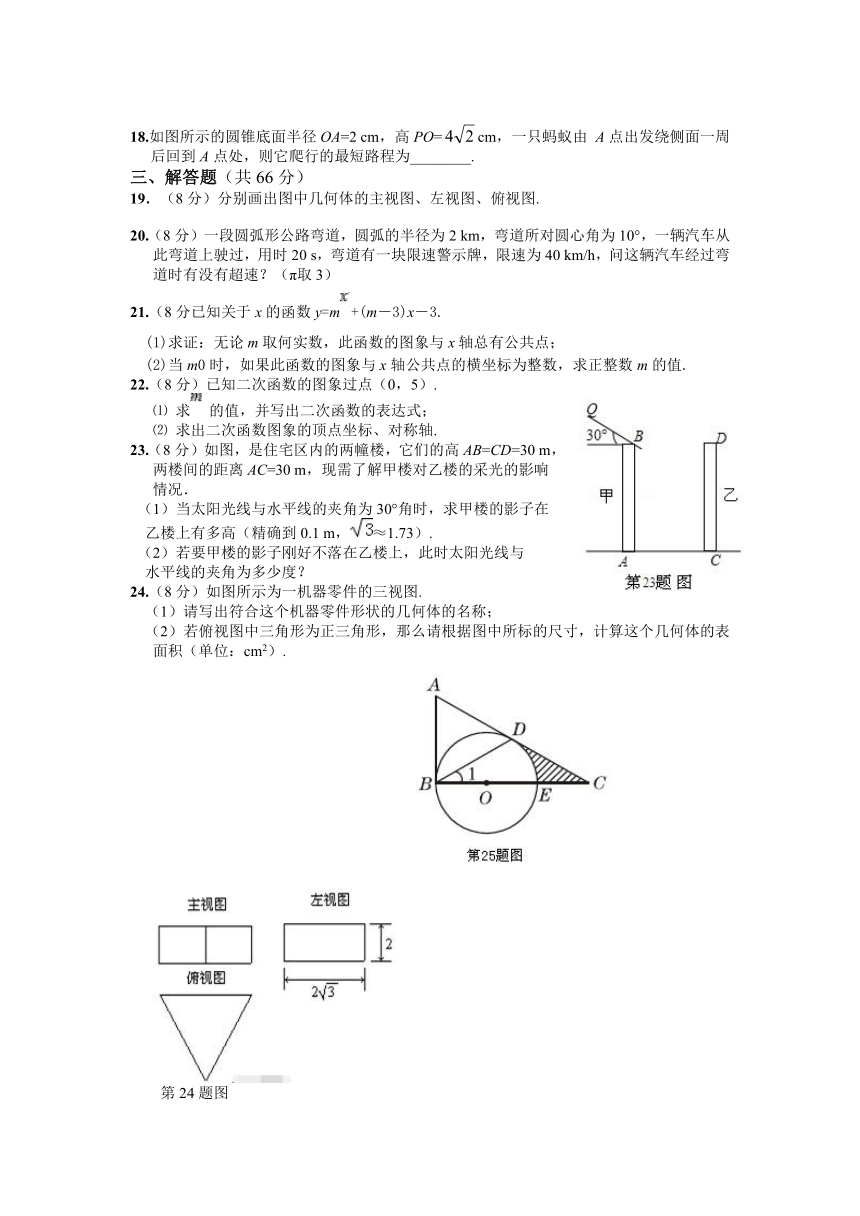
9.(2015·福建泉州中考)在同一平面直角坐标系中,函数y=+bx与y=bx+a的图象可能是( )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
10.函数的部分图象与的交点分别为A(1,0),B(0,3),对称轴是直线,在下列结论中,错误的是( )
A.顶点坐标为(-1,4) B.函数的表达式为
C.当 D.抛物线与轴的另一个交点是(-3,0)
二、填空题(每小题3分,共24分)
11.小军晚上到广场去玩,他发现有两人的 ( http: / / www.21cnjy.com )影子一个向东,一个向西,于是他肯定地说:“广场上的大灯泡一定位于两人 ”.
12.(2015·湖南益阳中考)甲、乙、丙三位好朋友随机站成一排照合影,甲没有站在中间的概率为 .
13.如果函数是二次函数,那么k的值一定是 .
14.已知二次函数y=ax2+bx+c(a ( http: / / www.21cnjy.com )≠0)的图象如图所示,且关于x的一元二次方程ax2+ bx+c-m=0没有实数根,有下列结论:①b2-4ac>0;②abc<0;③m>2.其中,正确的是 .
第15题图
15. 如图所示,下列四个几何体中,它们各 ( http: / / www.21cnjy.com )自的三视图(主视图、左视图、俯视图)有两个相同,而另一个不同的几何体是 .(把所有符合条件的都写上)
16.已知△ABC内接于⊙O,且,⊙O的半径等于6 ,O点到BC的距离OD等于3 ,则AC的长为___________.
17.( 2015·山西中考)如图,四边形ABCD内接于⊙O,AB为⊙O的直径,点C为的中点.若∠A=40°,则∠B= 度.
( http: / / www.21cnjy.com )
第17题图
18.如图所示的圆锥底面半径OA=2 cm,高PO=cm,一只蚂蚁由 A点出发绕侧面一周后回到A点处,则它爬行的最短路程为________.
三、解答题(共66分)
19.(8分)分别画出图中几何体的主视图、左视图、俯视图.
20.(8分)一段圆弧形公 ( http: / / www.21cnjy.com )路弯道,圆弧的半径为2 km,弯道所对圆心角为10°,一辆汽车从此弯道上驶过,用时20 s,弯道有一块限速警示牌,限速为40 km/h,问这辆汽车经过弯道时有没有超速?(π取3)
21.(8分已知关于x的函数y=m+(m-3)x-3.
(1)求证:无论m取何实数,此函数的图象与x轴总有公共点;
(2)当m0时,如果此函数的图象与x轴公共点的横坐标为整数,求正整数m的值.
22.(8分)已知二次函数的图象过点(0,5).
⑴ 求的值,并写出二次函数的表达式;
⑵ 求出二次函数图象的顶点坐标、对称轴.
23.(8分)如图,是住宅区内的两幢楼,它们的高AB=CD=30 m,
两楼间的距离AC=30 m,现需了解甲楼对乙楼的采光的影响
情况.
(1)当太阳光线与水平线的夹角为30°角时,求甲楼的影子在
乙楼上有多高(精确到0.1 m,≈1.73).
(2)若要甲楼的影子刚好不落在乙楼上,此时太阳光线与
水平线的夹角为多少度?
24.(8分)如图所示为一机器零件的三视图.
(1)请写出符合这个机器零件形状的几何体的名称;
(2)若俯视图中三角形为正三角形,那么请根据图中所标的尺寸,计算这个几何体的表面积(单位:cm2).
HYPERLINK "http://www.21cnjy.com"
第24题图
25.(8分)如图,在△ABC中,∠A ( http: / / www.21cnjy.com )BC=90°,D是边AC上的一点,连接BD ,使∠A=2∠1,E 是 BC上的一点,以 BE为直径的圆O经过点D.
(1)求证:AC 是圆O的切线;
(2)若∠A= 60°,圆O的半径为 2 ,求阴影部分的面积. (结果保留根号和π)
26.(10分)某公司经销一种绿茶,每千克成本为50元.市场调查发现,在一段时间内,销售量(kg)随销售单价(元/ kg)的变化而变化,具体关系式为:,且物价部门规定这种绿茶的销售单价不得高于90元/ kg.设这种绿茶在这段时间内的销售利润为(元),解答下列问题:
(1)求与的函数表达式.
(2)当取何值时,的值最大?
(3)如果公司想要在这段时间内获得2 250元的销售利润,销售单价应定为多少元?
期末检测题参考答案
1.C 解析:由二次函数的表达式可知,抛物线的顶点坐标为(1,-3),所以抛物线的对称轴是直线x=1.
2.B 解析:根据三视图的知识,主视图为一个矩形且有一条虚线,左视图为一个矩形,俯视图为一个三角形,符合条件的只有直三棱柱.
3.C 解析:∵ ,∴ ,∴ 弦三等分半圆,∴ 弦、弦所对的圆心角均为60°,∴ ∠=.
4.B 解析:圆锥的侧面积=×1×2=2(m ).
5.C 解析:根据圆周角定理,得∠BOC=2∠A=,所以CE=4sin =,根据垂径定理,得CD=2CE=.
6.D 解析:跟物体的摆放位置有关.
7.B 解析:由∠BAE=∠EA ( http: / / www.21cnjy.com )C,∠ABC=∠AEC,得△ABD∽△AEC; 由∠BAE=∠BCE, ∠ABC=∠AEC,得△ABD∽△CED.共2个.
8.C 解析:本题考查了圆的周长公式 .∵ 的半径,, ∴ 弧的长为.
9.C 解析:选项A:函数y=ax2+bx 中,a>0,b<0.
函数y=bx+a中,a>0,b>0.
选项B:函数y=ax2+bx 中,a>0,b>0.
函数y=bx+a中,a<0,b<0.
选项C:函数y=ax2+bx 中,a<0,b>0.
函数y=bx+a中,a<0,b>0.
选项D:函数y=ax2+bx 中,a<0,b<0.
函数y=bx+a中,a>0,b>0.
综上可得选项A,B,D是错误的,只有选项C正确.
10.C 解析:将点A(1,0),B(0,3)的坐标分别代入函数表达式,得
解得则函数表达式为.
将=-1代入函数表达式可得其顶点坐标为(-1,4).
当=0时可得,,解得
可见,抛物线与轴的另一个交点是(-3,0).
画出函数的图象可知,当<-1时,随的增大而增大.
可见,C选项错误.故选C.
11.中间的上方
12. 解析:甲、乙、丙三位好朋友站成一排照合影有以下可能:甲乙丙,甲丙乙,乙甲丙,乙丙甲,丙甲乙,丙乙甲,共6种情况,甲没有站在中间的情况有4种,所以甲没有站在中间的概率是.
13.0 解析:根据二次函数的定义,得,解得.
又∵ ,∴ .∴ 当时,这个函数是二次函数.
14. ①②③ 解析:∵ 抛物线与轴有两个交点,∴ 方程有两个不相等的实数根,∴ ,①正确.∵ 抛物线的开口向下,∴ .
又∵抛物线的对称轴是直线,,∴.∵ 抛物线与轴交于正半轴,∴,∴,②正确.方程的根是抛物线与直线交点的横坐标,当时,抛物线与直线没有交点,此时方程没有实数根,③正确.
15. ①③ 解析:①只有主视图和俯视图相同,③只有主视图和左视图相同.
16. 或6 解析:分两种情况:
(1)假设∠BAC是锐角,如图(1),则△ABC是锐角三角形,∵ AB=AC,∴ 点A是优弧BC的中点.∵ OD⊥BC,,根据垂径定理推论可知,DO的延长线必过点A,连接BO,∵ ,∴ .
在Rt△ADB中,,∴ .(2)若∠BAC是钝角,则△ABC是钝角三角形,如图(2),连接OB,则.
∵ OD⊥BC,,∴的延长线必过点A.
在Rt△ADB中,,
∴ .
综上所述,AC= 或6 .
17. 70 解析:如图所示,连接OC,OD,则∠A,∠BOD分别是所对的圆周角和圆心角,∵ ∠A=40°,∴ ∠BOD=80°.又点C为的中点,
∴ ,∴ ∠BOC=∠COD∠BOD=40°.
∵ OC=OB,∴ ∠B=∠OCB,
∴ ∠B70°.
18.cm 解析:圆锥的侧面展开图如图所示,设
∠,
由OA=2 cm,高PO= cm,得PA=6 cm,弧AA′=4 cm,
则,解得.过点P作,由,得∠.
又cm,所以,所以 cm.
19.分析:从正面看从左往右4列正方形的个数依
次为1,3,1,1;从左面看从左往右3列正方
形的个数依次为3,1,1;从上面看从左往右
4列正方形的个数依次为1,3,1,1.
解:如图所示.
20.分析:先根据弧长公式计算出弯道的长度,再
根据所用时间得出汽车的速度,再判断这辆汽
车经过弯道时有没有超速.
解:∵ ,∴ 汽车的速度为
(km/h),
60 km/h>40 km/h,∴ 这辆汽车经过弯道时超速.
21.解:(1)当m=0时,y=-3x-3,与x轴交于(-1,0).
当m≠0时,令y=0,则y=m+(m-3)x-3=0.
Δ=+12m=+6m+9=≥0.
∴ 无论m取何实数,此函数的图象都与x轴总有公共点.
(2)+(m-3)x-3=0,
∴ =-1,=.
因为是整数且m0,∴ 为整数,∴ m=1或m=3.
22.解:(1)将代入函数表达式,得,所以,所以;
(2),所以顶点坐标是(-3,-4),对称轴是直线.
23.解:(1)如图,连接CB并延长,延长QB交DC于点E,
作EF⊥AB,交AB于F,CE为甲楼在乙楼上的影子.
在Rt△BEF中,
∵EF=AC=30 m,∠FEB=30°,∴BE=2BF.设BF=x,则BE=2x.
根据勾股定理知BE2=BF2+EF2,∴(2x)2=x2+302,
∴x≈17.3(m)(负值舍去),∴EC=30﹣17.3=12.7(m).
(2)当甲楼的影子刚好落在点C处时,△ABC为等腰直角三
角形,
因此,当太阳光线与水平线夹角为45°时,甲楼的影子刚好
不落在乙楼上.
24. 解:(1)符合这个机器零件形状的几何体是直三棱柱.
(2)如图所示,△是正三角形,⊥,2,
∴ ,
(cm2).
第
24题答图
25.分析:(1)连接 OD,证出∠A=∠D ( http: / / www.21cnjy.com )OC,推出∠ODC=90°,根据切线的判定定理得出结论; (2)先求出Rt△ODC 的面积,再求出扇形ODE 的面积,即可求出阴影部分的面积.
(1)证明:如图,连接 OD,
∵ OB = OD,∴ ∠1 =∠2,∴ ∠DOC=2∠1.
∵ ∠A=2∠1,∴ ∠A=∠DOC.
∵ ∠ABC=90°,∴ ∠A+∠C=90°,
∴ ∠DOC+∠C= 90°,∴∠ODC=90°.
∵ OD 为半径,∴ AC 是圆O的切线.
(2)解:∠DOC=∠A=60°,OD=2,
在 Rt△ODC 中,tan 60°=,
DC=OD·tan 60°=2×=2,
SRt△ODC=×2×2=2,
=,
S阴影= SRt△ODC-=2-.
26.分析:(1)因为,
故与的函数表达式为.
(2)用配方法化简表达式求出取最大值x的取值即可.
(3)令时,求出即可.
解:(1),
∴ 与的关系式为.
(2),
∴ 当时,的值最大.
(3)当时,可得方程.
解这个方程,得.
根据题意,不合题意,应舍去.
∴ 当销售单价为75元/千克时,可获得销售利润2 250元.
A
(本检测题满分:120分,时间:120分钟)
一、选择题(每小题3分,共30分)
1.抛物线y=的对称轴是( )
A.y轴 B.直线x=-1 C.直线x=1 D.直线x=-3
2.(2015·湖南益阳中考)一个几何体的三视图如图所示,则这个几何体是( )
A.三棱锥 B.三棱柱 C.圆柱 D.长方体
3.如图,AB是⊙O的直径,BC,CD,DA是⊙O的弦,且,则∠( )
A.100° B.110° C.120° D.135°
4.如图,一把遮阳伞撑开时母线的长是2 m,底面半径为1 m,则做这把遮阳伞需用布料的面积是( )
A. m B. m
C. m D. m
5.如图,圆O的直径AB垂直于弦CD,垂足是E,∠A=22.5°,OC=4,CD 的长为( )
A. B.4
C. D.8
6.两个不同长度的物体在同一时刻同一地点的太阳光下得到的投影长
度的关系是 ( )
A.相等 B.长的较长 C.短的较长 D.不能确定
7.如图,△ABC的三个顶点都在⊙O上,∠BAC的平分线交BC于点D,交⊙O于点E,则与△ABD相似的三角形有( )
A.3个 B.2个 C.1个 D.0个
8.如图,已知的半径,,则所对的弧的长为( )
A. B. C. D.
9.(2015·福建泉州中考)在同一平面直角坐标系中,函数y=+bx与y=bx+a的图象可能是( )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
10.函数的部分图象与的交点分别为A(1,0),B(0,3),对称轴是直线,在下列结论中,错误的是( )
A.顶点坐标为(-1,4) B.函数的表达式为
C.当 D.抛物线与轴的另一个交点是(-3,0)
二、填空题(每小题3分,共24分)
11.小军晚上到广场去玩,他发现有两人的 ( http: / / www.21cnjy.com )影子一个向东,一个向西,于是他肯定地说:“广场上的大灯泡一定位于两人 ”.
12.(2015·湖南益阳中考)甲、乙、丙三位好朋友随机站成一排照合影,甲没有站在中间的概率为 .
13.如果函数是二次函数,那么k的值一定是 .
14.已知二次函数y=ax2+bx+c(a ( http: / / www.21cnjy.com )≠0)的图象如图所示,且关于x的一元二次方程ax2+ bx+c-m=0没有实数根,有下列结论:①b2-4ac>0;②abc<0;③m>2.其中,正确的是 .
第15题图
15. 如图所示,下列四个几何体中,它们各 ( http: / / www.21cnjy.com )自的三视图(主视图、左视图、俯视图)有两个相同,而另一个不同的几何体是 .(把所有符合条件的都写上)
16.已知△ABC内接于⊙O,且,⊙O的半径等于6 ,O点到BC的距离OD等于3 ,则AC的长为___________.
17.( 2015·山西中考)如图,四边形ABCD内接于⊙O,AB为⊙O的直径,点C为的中点.若∠A=40°,则∠B= 度.
( http: / / www.21cnjy.com )
第17题图
18.如图所示的圆锥底面半径OA=2 cm,高PO=cm,一只蚂蚁由 A点出发绕侧面一周后回到A点处,则它爬行的最短路程为________.
三、解答题(共66分)
19.(8分)分别画出图中几何体的主视图、左视图、俯视图.
20.(8分)一段圆弧形公 ( http: / / www.21cnjy.com )路弯道,圆弧的半径为2 km,弯道所对圆心角为10°,一辆汽车从此弯道上驶过,用时20 s,弯道有一块限速警示牌,限速为40 km/h,问这辆汽车经过弯道时有没有超速?(π取3)
21.(8分已知关于x的函数y=m+(m-3)x-3.
(1)求证:无论m取何实数,此函数的图象与x轴总有公共点;
(2)当m0时,如果此函数的图象与x轴公共点的横坐标为整数,求正整数m的值.
22.(8分)已知二次函数的图象过点(0,5).
⑴ 求的值,并写出二次函数的表达式;
⑵ 求出二次函数图象的顶点坐标、对称轴.
23.(8分)如图,是住宅区内的两幢楼,它们的高AB=CD=30 m,
两楼间的距离AC=30 m,现需了解甲楼对乙楼的采光的影响
情况.
(1)当太阳光线与水平线的夹角为30°角时,求甲楼的影子在
乙楼上有多高(精确到0.1 m,≈1.73).
(2)若要甲楼的影子刚好不落在乙楼上,此时太阳光线与
水平线的夹角为多少度?
24.(8分)如图所示为一机器零件的三视图.
(1)请写出符合这个机器零件形状的几何体的名称;
(2)若俯视图中三角形为正三角形,那么请根据图中所标的尺寸,计算这个几何体的表面积(单位:cm2).
HYPERLINK "http://www.21cnjy.com"
第24题图
25.(8分)如图,在△ABC中,∠A ( http: / / www.21cnjy.com )BC=90°,D是边AC上的一点,连接BD ,使∠A=2∠1,E 是 BC上的一点,以 BE为直径的圆O经过点D.
(1)求证:AC 是圆O的切线;
(2)若∠A= 60°,圆O的半径为 2 ,求阴影部分的面积. (结果保留根号和π)
26.(10分)某公司经销一种绿茶,每千克成本为50元.市场调查发现,在一段时间内,销售量(kg)随销售单价(元/ kg)的变化而变化,具体关系式为:,且物价部门规定这种绿茶的销售单价不得高于90元/ kg.设这种绿茶在这段时间内的销售利润为(元),解答下列问题:
(1)求与的函数表达式.
(2)当取何值时,的值最大?
(3)如果公司想要在这段时间内获得2 250元的销售利润,销售单价应定为多少元?
期末检测题参考答案
1.C 解析:由二次函数的表达式可知,抛物线的顶点坐标为(1,-3),所以抛物线的对称轴是直线x=1.
2.B 解析:根据三视图的知识,主视图为一个矩形且有一条虚线,左视图为一个矩形,俯视图为一个三角形,符合条件的只有直三棱柱.
3.C 解析:∵ ,∴ ,∴ 弦三等分半圆,∴ 弦、弦所对的圆心角均为60°,∴ ∠=.
4.B 解析:圆锥的侧面积=×1×2=2(m ).
5.C 解析:根据圆周角定理,得∠BOC=2∠A=,所以CE=4sin =,根据垂径定理,得CD=2CE=.
6.D 解析:跟物体的摆放位置有关.
7.B 解析:由∠BAE=∠EA ( http: / / www.21cnjy.com )C,∠ABC=∠AEC,得△ABD∽△AEC; 由∠BAE=∠BCE, ∠ABC=∠AEC,得△ABD∽△CED.共2个.
8.C 解析:本题考查了圆的周长公式 .∵ 的半径,, ∴ 弧的长为.
9.C 解析:选项A:函数y=ax2+bx 中,a>0,b<0.
函数y=bx+a中,a>0,b>0.
选项B:函数y=ax2+bx 中,a>0,b>0.
函数y=bx+a中,a<0,b<0.
选项C:函数y=ax2+bx 中,a<0,b>0.
函数y=bx+a中,a<0,b>0.
选项D:函数y=ax2+bx 中,a<0,b<0.
函数y=bx+a中,a>0,b>0.
综上可得选项A,B,D是错误的,只有选项C正确.
10.C 解析:将点A(1,0),B(0,3)的坐标分别代入函数表达式,得
解得则函数表达式为.
将=-1代入函数表达式可得其顶点坐标为(-1,4).
当=0时可得,,解得
可见,抛物线与轴的另一个交点是(-3,0).
画出函数的图象可知,当<-1时,随的增大而增大.
可见,C选项错误.故选C.
11.中间的上方
12. 解析:甲、乙、丙三位好朋友站成一排照合影有以下可能:甲乙丙,甲丙乙,乙甲丙,乙丙甲,丙甲乙,丙乙甲,共6种情况,甲没有站在中间的情况有4种,所以甲没有站在中间的概率是.
13.0 解析:根据二次函数的定义,得,解得.
又∵ ,∴ .∴ 当时,这个函数是二次函数.
14. ①②③ 解析:∵ 抛物线与轴有两个交点,∴ 方程有两个不相等的实数根,∴ ,①正确.∵ 抛物线的开口向下,∴ .
又∵抛物线的对称轴是直线,,∴.∵ 抛物线与轴交于正半轴,∴,∴,②正确.方程的根是抛物线与直线交点的横坐标,当时,抛物线与直线没有交点,此时方程没有实数根,③正确.
15. ①③ 解析:①只有主视图和俯视图相同,③只有主视图和左视图相同.
16. 或6 解析:分两种情况:
(1)假设∠BAC是锐角,如图(1),则△ABC是锐角三角形,∵ AB=AC,∴ 点A是优弧BC的中点.∵ OD⊥BC,,根据垂径定理推论可知,DO的延长线必过点A,连接BO,∵ ,∴ .
在Rt△ADB中,,∴ .(2)若∠BAC是钝角,则△ABC是钝角三角形,如图(2),连接OB,则.
∵ OD⊥BC,,∴的延长线必过点A.
在Rt△ADB中,,
∴ .
综上所述,AC= 或6 .
17. 70 解析:如图所示,连接OC,OD,则∠A,∠BOD分别是所对的圆周角和圆心角,∵ ∠A=40°,∴ ∠BOD=80°.又点C为的中点,
∴ ,∴ ∠BOC=∠COD∠BOD=40°.
∵ OC=OB,∴ ∠B=∠OCB,
∴ ∠B70°.
18.cm 解析:圆锥的侧面展开图如图所示,设
∠,
由OA=2 cm,高PO= cm,得PA=6 cm,弧AA′=4 cm,
则,解得.过点P作,由,得∠.
又cm,所以,所以 cm.
19.分析:从正面看从左往右4列正方形的个数依
次为1,3,1,1;从左面看从左往右3列正方
形的个数依次为3,1,1;从上面看从左往右
4列正方形的个数依次为1,3,1,1.
解:如图所示.
20.分析:先根据弧长公式计算出弯道的长度,再
根据所用时间得出汽车的速度,再判断这辆汽
车经过弯道时有没有超速.
解:∵ ,∴ 汽车的速度为
(km/h),
60 km/h>40 km/h,∴ 这辆汽车经过弯道时超速.
21.解:(1)当m=0时,y=-3x-3,与x轴交于(-1,0).
当m≠0时,令y=0,则y=m+(m-3)x-3=0.
Δ=+12m=+6m+9=≥0.
∴ 无论m取何实数,此函数的图象都与x轴总有公共点.
(2)+(m-3)x-3=0,
∴ =-1,=.
因为是整数且m0,∴ 为整数,∴ m=1或m=3.
22.解:(1)将代入函数表达式,得,所以,所以;
(2),所以顶点坐标是(-3,-4),对称轴是直线.
23.解:(1)如图,连接CB并延长,延长QB交DC于点E,
作EF⊥AB,交AB于F,CE为甲楼在乙楼上的影子.
在Rt△BEF中,
∵EF=AC=30 m,∠FEB=30°,∴BE=2BF.设BF=x,则BE=2x.
根据勾股定理知BE2=BF2+EF2,∴(2x)2=x2+302,
∴x≈17.3(m)(负值舍去),∴EC=30﹣17.3=12.7(m).
(2)当甲楼的影子刚好落在点C处时,△ABC为等腰直角三
角形,
因此,当太阳光线与水平线夹角为45°时,甲楼的影子刚好
不落在乙楼上.
24. 解:(1)符合这个机器零件形状的几何体是直三棱柱.
(2)如图所示,△是正三角形,⊥,2,
∴ ,
(cm2).
第
24题答图
25.分析:(1)连接 OD,证出∠A=∠D ( http: / / www.21cnjy.com )OC,推出∠ODC=90°,根据切线的判定定理得出结论; (2)先求出Rt△ODC 的面积,再求出扇形ODE 的面积,即可求出阴影部分的面积.
(1)证明:如图,连接 OD,
∵ OB = OD,∴ ∠1 =∠2,∴ ∠DOC=2∠1.
∵ ∠A=2∠1,∴ ∠A=∠DOC.
∵ ∠ABC=90°,∴ ∠A+∠C=90°,
∴ ∠DOC+∠C= 90°,∴∠ODC=90°.
∵ OD 为半径,∴ AC 是圆O的切线.
(2)解:∠DOC=∠A=60°,OD=2,
在 Rt△ODC 中,tan 60°=,
DC=OD·tan 60°=2×=2,
SRt△ODC=×2×2=2,
=,
S阴影= SRt△ODC-=2-.
26.分析:(1)因为,
故与的函数表达式为.
(2)用配方法化简表达式求出取最大值x的取值即可.
(3)令时,求出即可.
解:(1),
∴ 与的关系式为.
(2),
∴ 当时,的值最大.
(3)当时,可得方程.
解这个方程,得.
根据题意,不合题意,应舍去.
∴ 当销售单价为75元/千克时,可获得销售利润2 250元.
A
同课章节目录
