沪科版数学八年级上册 第11章 平面直角坐标系 单元测试(含答案)
文档属性
| 名称 | 沪科版数学八年级上册 第11章 平面直角坐标系 单元测试(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-06 00:00:00 | ||
图片预览


文档简介
第11 章 平面直角坐标系
考点一 在平面内确定点的位置
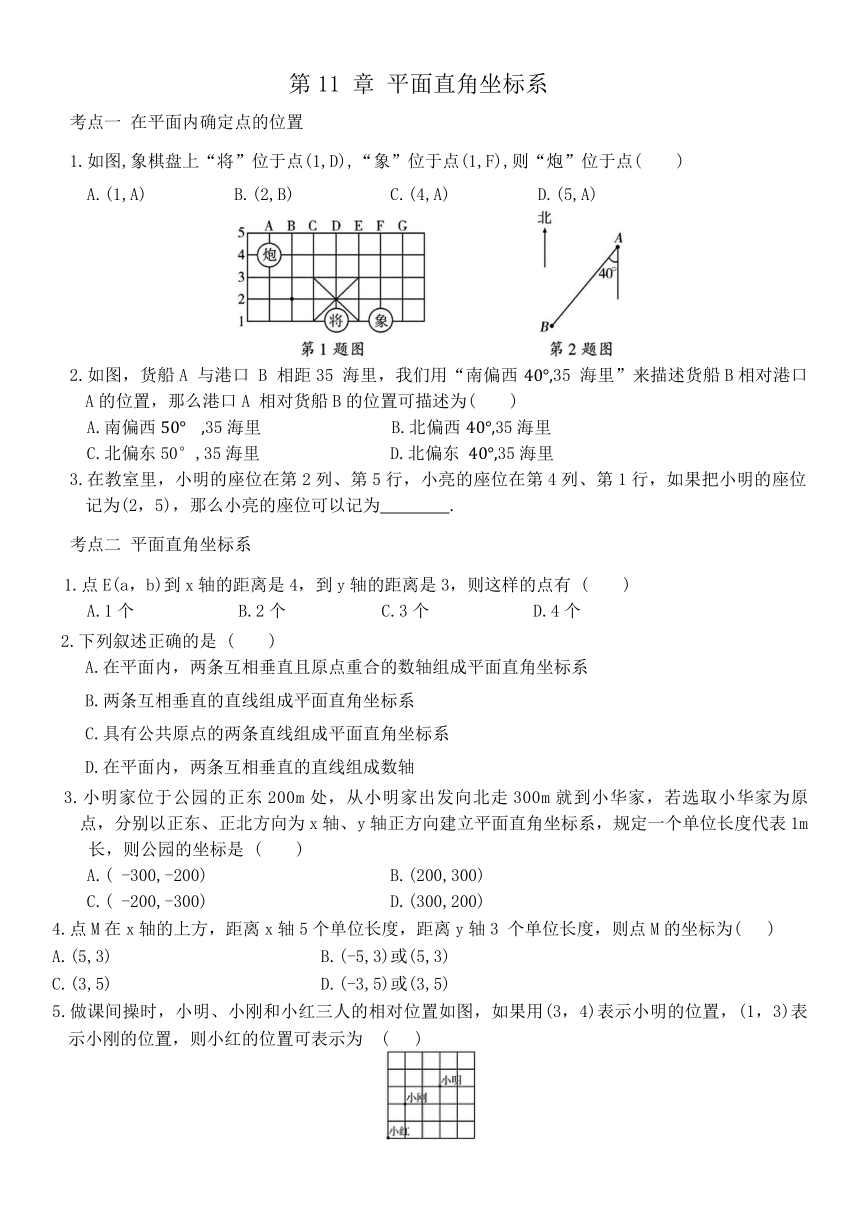
1.如图,象棋盘上“将”位于点(1,D),“象”位于点(1,F),则“炮”位于点( )
A.(1,A) B.(2,B) C.(4,A) D.(5,A)
2.如图,货船A 与港口 B 相距35 海里,我们用“南偏西 35 海里”来描述货船B相对港口A的位置,那么港口A 相对货船B的位置可描述为( )
A.南偏西35海里 B.北偏西 35海里
C.北偏东50°,35海里 D.北偏东 35海里
3.在教室里,小明的座位在第2列、第5行,小亮的座位在第4列、第1行,如果把小明的座位记为(2,5),那么小亮的座位可以记为 .
考点二 平面直角坐标系
1.点E(a,b)到x轴的距离是4,到y轴的距离是3,则这样的点有 ( )
A.1个 B.2个 C.3个 D.4个
2.下列叙述正确的是 ( )
A.在平面内,两条互相垂直且原点重合的数轴组成平面直角坐标系
B.两条互相垂直的直线组成平面直角坐标系
C.具有公共原点的两条直线组成平面直角坐标系
D.在平面内,两条互相垂直的直线组成数轴
3.小明家位于公园的正东200m处,从小明家出发向北走300m就到小华家,若选取小华家为原点,分别以正东、正北方向为x轴、y轴正方向建立平面直角坐标系,规定一个单位长度代表1m 长,则公园的坐标是 ( )
A.( -300,-200) B.(200,300)
C.( -200,-300) D.(300,200)
4.点M在x轴的上方,距离x轴5个单位长度,距离y轴3 个单位长度,则点M的坐标为( )
A.(5,3) B.(-5,3)或(5,3)
C.(3,5) D.(-3,5)或(3,5)
5.做课间操时,小明、小刚和小红三人的相对位置如图,如果用(3,4)表示小明的位置,(1,3)表示小刚的位置,则小红的位置可表示为 ( )
A.(0,0) B.(0,1) C.(1,0) D.(1,2)
6.已知点C在y轴上,它与原点的距离是5个单位长度,则点 C的坐标是
7.如图是某市区几个旅游景点的示意图(图中每个小正方形的边长为1 个单位长度),若光岳楼的坐标为(-3,1),请建立平面直角坐标系,并用坐标表示动物园的位置.
考点三 象限及平面内点的坐标特征
1.在平面直角坐标系中,下列各点在第三象限的是 ( )
B.(-2,1) C.(2,-1) D.( -2,-1)
2.若点P是平面直角坐标系中第二象限内的点,且点P到x轴的距离是2,到y轴的距离是3,则点 P的坐标是 ( )
A.( -2,3) B.(2,-3) C.(-3,2) D.(3,-2)
3.如果P(ab,a+b)在第四象限,那么Q(a,-b)在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
4.在平面直角坐标系中,若点P(m+3,m-1)在第一象限,则m的取值范围是 ( )
A. -31
C. m< -3 D. m>-3
5.在平面直角坐标系中,点 到两坐标轴上的距离相等,则m的值为( )
A.4 D.4或
6.已知在平面直角坐标系中,点 在坐标轴上,则a的值为( )
A. a= -1 或
C. a=1或
7.若点P(a,b)在第四象限,则点 在第 象限.
8.以方程组 的解为坐标的点(x,y)在平面直角坐标系中的位置是第 象限.
9.在平面直角坐标系中,有一点 ,试求满足下列条件的m的值,
(1)点P在x轴上;
(2)点 P 在第三象限;
(3)点P 到y轴距离是1.
考点四 平面直角坐标系内图形的面积
1.在平面直角坐标系中,若A点的坐标为( B点的坐标为(2,0),则三角形ABO的面积为( )
A.15 B.7.5 C.6 D.3
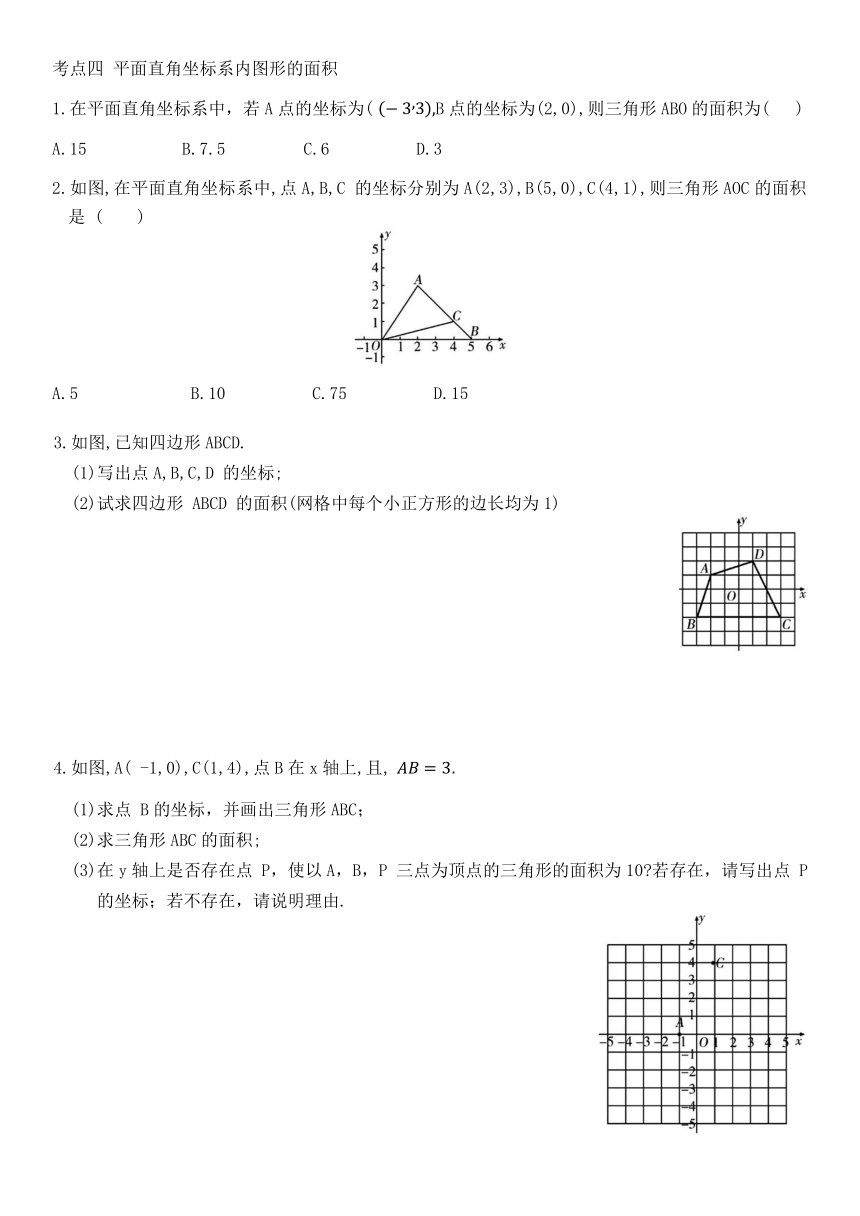
2.如图,在平面直角坐标系中,点A,B,C 的坐标分别为A(2,3),B(5,0),C(4,1),则三角形AOC的面积是 ( )
A.5 B.10 C.75 D.15
3.如图,已知四边形ABCD.
(1)写出点A,B,C,D 的坐标;
(2)试求四边形 ABCD 的面积(网格中每个小正方形的边长均为1)
4.如图,A( -1,0),C(1,4),点B在x轴上,且,
(1)求点 B的坐标,并画出三角形ABC;
(2)求三角形ABC的面积;
(3)在y轴上是否存在点 P,使以A,B,P 三点为顶点的三角形的面积为10 若存在,请写出点 P的坐标;若不存在,请说明理由.
考点五 点在平面直角坐标系中的平移
1.点 )向左平移3 个单位,再向上平移4 个单位到点 B,则点 B的坐标为 ( )
2.在平面直角坐标系中,有C(1,2),D(1,-1)两点,则点 C 可由点D( )
A.向上平移3个单位得到
B.向下平移3个单位得到
C.向左平移1个单位得到
D.向右平移1个单位得到
3.在平面直角坐标系中,将点A(m,n)先向右平移2个单位,再向上平移3个单位,得到点A',若点A'位于第二象限,则m,n的取值范围分别是( )
A. m<2,n>3 B. m<2,n>-3
C. m< -2,n< -3 D. m< -2,n> -3
4.在平面直角坐标系中,已知点A的坐标为(m,3).若将点A先向下平移2个单位,再向左平移1个单位后得到点B(1,n),则m+n= .
5.在平面直角坐标系中,一只蚂蚁先向上爬4个单位,再向左爬3个单位后,到达(0,0),则它最开始所在位置的坐标是 .
6.将点P(m+2,2m+4)向右平移1个单位到点Q,且点Q恰好在y轴上,那么点Q的坐标是 .
7.已知平面直角坐标系内的点A(-2,5),若将平面直角坐标系先向右平移3个单位,再向上平移4个单位,则点A在平移后的平面直角坐标系中的坐标是 .
考点六 图形在平面直角坐标系中的平移
1.三角形A'B'C'是由三角形ABC平移得到的,点A( -1,-4)的对应点为A'(1,-1),则点B(1,1)的对应点B'、点C( -1,4)的对应点C'的坐标分别为 ( )
A.(2,2),(3,4) B.(3,4),(1,7)
C.( -2,2),(1,7) D.(3,4),(2,-2)
2.四边形ABCD经过平移得到四边形A'B'C'D',若点 A(a,b)的对应点为A'(a-3,b+2),则对四边形ABCD进行的变换是 ( )
A.先向上平移3 个单位,再向右平移2 个单位
B.先向下平移3 个单位,再向左平移2 个单位
C.先向右平移3 个单位,再向下平移2 个单位
D.先向左平移3 个单位,再向上平移2 个单位
3.若线段CD是由线段AB平移得到的,点A( -2,3)的对应点为C(3,6),则点 B(-5,-2)的对应点D的坐标是 .
4.三角形ABC与三角形A'B'C'在平面直角坐标系中的位置如图所示,三角形A'B'C'是由三角形ABC经过平移得到的.
(1)分别写出点. 的坐标;
(2)说明三角形. 是由三角形ABC经过怎样的平移得到的;
(3)若点P(a,b)是三角形ABC 内的一点,则平移后点 P 在三角形. 内的对应点为 P',写出点. 的坐标.
5.如图,将三角形ABC向右平移3个单位,再向下平移2个单位,得到对应的三角形
(1)画出三角形. 并写出点. 的坐标;
(2)求三角形 的面积.
第11章 平面直角坐标系
考点一在平面内确定点的位置
1. C 2. D 3.(4,1)
考点二 平面直角坐标系
1. D 2. A 3. C 4. D 5. B 6.(0,5)或(0,-5)
7.解:建立平面直角坐标系如图.
动物园的坐标为(4,4).
考点三 象限及平面内点的坐标特征
1. D 2. C 3. B 4. B 5. D 6. B 7.二 8.四
9.解:(1)要使点P在x轴上,m应满足2m-6=0,解得m=3.
∴当m=3时,点P在x轴上.
(2)要使点 P在第三象限,m应满足 解得1∴当1(3)要使点P到y轴距离是1,m应满足|-m+1|=1,解得m=2或m=0.
∴当m=2或m=0时,点P到y轴距离是1.
考点四 平面直角坐标系内图形的面积
1. D 2. A
3.解:(1)A(-2,1),B( -3,-2),C(3,-2),D(1,2).
(2)作AE⊥BC 于点E,DG⊥BC 于点 G.
则S四边形ABCD =S△ABE +S△DGC +S梯形AEGD =
4.解:(1)点B在点A的右边时,-1+3=2,点B在点A的左边时,-1-3= -4,∴ 点 B的坐标为(2,0)或( -4,0).画出三角形ABC 如图.
(2)三角形ABC的面积
(3)设点P到x轴的距离为h,则 10,解得 点 P 在y轴正半轴时, 点 P 在 y轴负半轴时,
综上所述,点P的坐标为(0, )或(
考点五 点在平面直角坐标系中的平移
1. C 2. A 3. D
4.3 5.(3,-4) 6.(0,-2) 7.(-5,1)
考点六 图形在平面直角坐标系中的平移
1. B 2. D 3.(0,1)
4.解:(1)A'(-3,1),B'(-2,-2),C'(-1,-1).
(2)三角形A'B'C'是由三角形ABC 先向左平移4个单位长度,再向下平移2个单位长度得到的.
(3)点 P'的坐标为((a-4,b-2).
5.解:(1)如图,三角形A B C 即为所求.A (1,3),B ( -2,-4),C (6,1)
(2)三角形 的面积
考点一 在平面内确定点的位置
1.如图,象棋盘上“将”位于点(1,D),“象”位于点(1,F),则“炮”位于点( )
A.(1,A) B.(2,B) C.(4,A) D.(5,A)
2.如图,货船A 与港口 B 相距35 海里,我们用“南偏西 35 海里”来描述货船B相对港口A的位置,那么港口A 相对货船B的位置可描述为( )
A.南偏西35海里 B.北偏西 35海里
C.北偏东50°,35海里 D.北偏东 35海里
3.在教室里,小明的座位在第2列、第5行,小亮的座位在第4列、第1行,如果把小明的座位记为(2,5),那么小亮的座位可以记为 .
考点二 平面直角坐标系
1.点E(a,b)到x轴的距离是4,到y轴的距离是3,则这样的点有 ( )
A.1个 B.2个 C.3个 D.4个
2.下列叙述正确的是 ( )
A.在平面内,两条互相垂直且原点重合的数轴组成平面直角坐标系
B.两条互相垂直的直线组成平面直角坐标系
C.具有公共原点的两条直线组成平面直角坐标系
D.在平面内,两条互相垂直的直线组成数轴
3.小明家位于公园的正东200m处,从小明家出发向北走300m就到小华家,若选取小华家为原点,分别以正东、正北方向为x轴、y轴正方向建立平面直角坐标系,规定一个单位长度代表1m 长,则公园的坐标是 ( )
A.( -300,-200) B.(200,300)
C.( -200,-300) D.(300,200)
4.点M在x轴的上方,距离x轴5个单位长度,距离y轴3 个单位长度,则点M的坐标为( )
A.(5,3) B.(-5,3)或(5,3)
C.(3,5) D.(-3,5)或(3,5)
5.做课间操时,小明、小刚和小红三人的相对位置如图,如果用(3,4)表示小明的位置,(1,3)表示小刚的位置,则小红的位置可表示为 ( )
A.(0,0) B.(0,1) C.(1,0) D.(1,2)
6.已知点C在y轴上,它与原点的距离是5个单位长度,则点 C的坐标是
7.如图是某市区几个旅游景点的示意图(图中每个小正方形的边长为1 个单位长度),若光岳楼的坐标为(-3,1),请建立平面直角坐标系,并用坐标表示动物园的位置.
考点三 象限及平面内点的坐标特征
1.在平面直角坐标系中,下列各点在第三象限的是 ( )
B.(-2,1) C.(2,-1) D.( -2,-1)
2.若点P是平面直角坐标系中第二象限内的点,且点P到x轴的距离是2,到y轴的距离是3,则点 P的坐标是 ( )
A.( -2,3) B.(2,-3) C.(-3,2) D.(3,-2)
3.如果P(ab,a+b)在第四象限,那么Q(a,-b)在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
4.在平面直角坐标系中,若点P(m+3,m-1)在第一象限,则m的取值范围是 ( )
A. -3
C. m< -3 D. m>-3
5.在平面直角坐标系中,点 到两坐标轴上的距离相等,则m的值为( )
A.4 D.4或
6.已知在平面直角坐标系中,点 在坐标轴上,则a的值为( )
A. a= -1 或
C. a=1或
7.若点P(a,b)在第四象限,则点 在第 象限.
8.以方程组 的解为坐标的点(x,y)在平面直角坐标系中的位置是第 象限.
9.在平面直角坐标系中,有一点 ,试求满足下列条件的m的值,
(1)点P在x轴上;
(2)点 P 在第三象限;
(3)点P 到y轴距离是1.
考点四 平面直角坐标系内图形的面积
1.在平面直角坐标系中,若A点的坐标为( B点的坐标为(2,0),则三角形ABO的面积为( )
A.15 B.7.5 C.6 D.3
2.如图,在平面直角坐标系中,点A,B,C 的坐标分别为A(2,3),B(5,0),C(4,1),则三角形AOC的面积是 ( )
A.5 B.10 C.75 D.15
3.如图,已知四边形ABCD.
(1)写出点A,B,C,D 的坐标;
(2)试求四边形 ABCD 的面积(网格中每个小正方形的边长均为1)
4.如图,A( -1,0),C(1,4),点B在x轴上,且,
(1)求点 B的坐标,并画出三角形ABC;
(2)求三角形ABC的面积;
(3)在y轴上是否存在点 P,使以A,B,P 三点为顶点的三角形的面积为10 若存在,请写出点 P的坐标;若不存在,请说明理由.
考点五 点在平面直角坐标系中的平移
1.点 )向左平移3 个单位,再向上平移4 个单位到点 B,则点 B的坐标为 ( )
2.在平面直角坐标系中,有C(1,2),D(1,-1)两点,则点 C 可由点D( )
A.向上平移3个单位得到
B.向下平移3个单位得到
C.向左平移1个单位得到
D.向右平移1个单位得到
3.在平面直角坐标系中,将点A(m,n)先向右平移2个单位,再向上平移3个单位,得到点A',若点A'位于第二象限,则m,n的取值范围分别是( )
A. m<2,n>3 B. m<2,n>-3
C. m< -2,n< -3 D. m< -2,n> -3
4.在平面直角坐标系中,已知点A的坐标为(m,3).若将点A先向下平移2个单位,再向左平移1个单位后得到点B(1,n),则m+n= .
5.在平面直角坐标系中,一只蚂蚁先向上爬4个单位,再向左爬3个单位后,到达(0,0),则它最开始所在位置的坐标是 .
6.将点P(m+2,2m+4)向右平移1个单位到点Q,且点Q恰好在y轴上,那么点Q的坐标是 .
7.已知平面直角坐标系内的点A(-2,5),若将平面直角坐标系先向右平移3个单位,再向上平移4个单位,则点A在平移后的平面直角坐标系中的坐标是 .
考点六 图形在平面直角坐标系中的平移
1.三角形A'B'C'是由三角形ABC平移得到的,点A( -1,-4)的对应点为A'(1,-1),则点B(1,1)的对应点B'、点C( -1,4)的对应点C'的坐标分别为 ( )
A.(2,2),(3,4) B.(3,4),(1,7)
C.( -2,2),(1,7) D.(3,4),(2,-2)
2.四边形ABCD经过平移得到四边形A'B'C'D',若点 A(a,b)的对应点为A'(a-3,b+2),则对四边形ABCD进行的变换是 ( )
A.先向上平移3 个单位,再向右平移2 个单位
B.先向下平移3 个单位,再向左平移2 个单位
C.先向右平移3 个单位,再向下平移2 个单位
D.先向左平移3 个单位,再向上平移2 个单位
3.若线段CD是由线段AB平移得到的,点A( -2,3)的对应点为C(3,6),则点 B(-5,-2)的对应点D的坐标是 .
4.三角形ABC与三角形A'B'C'在平面直角坐标系中的位置如图所示,三角形A'B'C'是由三角形ABC经过平移得到的.
(1)分别写出点. 的坐标;
(2)说明三角形. 是由三角形ABC经过怎样的平移得到的;
(3)若点P(a,b)是三角形ABC 内的一点,则平移后点 P 在三角形. 内的对应点为 P',写出点. 的坐标.
5.如图,将三角形ABC向右平移3个单位,再向下平移2个单位,得到对应的三角形
(1)画出三角形. 并写出点. 的坐标;
(2)求三角形 的面积.
第11章 平面直角坐标系
考点一在平面内确定点的位置
1. C 2. D 3.(4,1)
考点二 平面直角坐标系
1. D 2. A 3. C 4. D 5. B 6.(0,5)或(0,-5)
7.解:建立平面直角坐标系如图.
动物园的坐标为(4,4).
考点三 象限及平面内点的坐标特征
1. D 2. C 3. B 4. B 5. D 6. B 7.二 8.四
9.解:(1)要使点P在x轴上,m应满足2m-6=0,解得m=3.
∴当m=3时,点P在x轴上.
(2)要使点 P在第三象限,m应满足 解得1
∴当m=2或m=0时,点P到y轴距离是1.
考点四 平面直角坐标系内图形的面积
1. D 2. A
3.解:(1)A(-2,1),B( -3,-2),C(3,-2),D(1,2).
(2)作AE⊥BC 于点E,DG⊥BC 于点 G.
则S四边形ABCD =S△ABE +S△DGC +S梯形AEGD =
4.解:(1)点B在点A的右边时,-1+3=2,点B在点A的左边时,-1-3= -4,∴ 点 B的坐标为(2,0)或( -4,0).画出三角形ABC 如图.
(2)三角形ABC的面积
(3)设点P到x轴的距离为h,则 10,解得 点 P 在y轴正半轴时, 点 P 在 y轴负半轴时,
综上所述,点P的坐标为(0, )或(
考点五 点在平面直角坐标系中的平移
1. C 2. A 3. D
4.3 5.(3,-4) 6.(0,-2) 7.(-5,1)
考点六 图形在平面直角坐标系中的平移
1. B 2. D 3.(0,1)
4.解:(1)A'(-3,1),B'(-2,-2),C'(-1,-1).
(2)三角形A'B'C'是由三角形ABC 先向左平移4个单位长度,再向下平移2个单位长度得到的.
(3)点 P'的坐标为((a-4,b-2).
5.解:(1)如图,三角形A B C 即为所求.A (1,3),B ( -2,-4),C (6,1)
(2)三角形 的面积
