沪科版数学八年级上册 第 十一 章 平 面直角坐标系 单元测试(含答案)
文档属性
| 名称 | 沪科版数学八年级上册 第 十一 章 平 面直角坐标系 单元测试(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 839.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-06 00:00:00 | ||
图片预览


文档简介
第 十一 章 平 面直角坐标系
(时间:120分钟满分:150分)
题号 一 二 三 四 五 六 七 八 总 分
得 分
一、选择题(本大题共10 小题,每小题4分,满分40 分)
1.平面直角坐标系内的下列各点中,在y轴上的点是 ( )
A.( -1,2) B.(-2,-3)
C.(0,3) D.(-3,0)
2.在平面直角坐标系中,点P 的坐标为(-3,5),则点 P 在 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
3.如图是天安门广场周围的景点分布示意图的一部分,若表示“王府井”的点的坐标为(4,1),表示“人民大会堂”的点的坐标为(0,-1),则表示“天安门”的点的坐标为 ( )
A.(0,0) B.(-1,0) C.(1,0) D.(1,1)
4.点M(-3,5)经过平移变换后得到点 N(3,5),则平移的方向和距离为( )
A.向上平移6 个单位 B.向左平移6 个单位
C.向右平移6个单位 D.向下平移6个单位
5.点P在第三象限,点P到x轴的距离是5,到y轴的距离是2,那么点P的坐标为 ( )
A.(-5,2) B.( -2,-5)
C.(-2,5) D.(2,-5)
6.已知点P( -3,-3),Q( -3,4),则直线PQ ( )
A.平行于x轴 B.平行于y轴
C.垂直于y轴 D.以上都不正确
7.无论 m取什么实数,点( 一定在 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
8.已知三角形ABC的顶点坐标分别是A(0,6),B( -3,-3),C(1,0),将三角形ABC平移后顶点A的对应点 A 的坐标是(4,10),则点 B的对应点B 的坐标为( )
A.(7,1) B.(1,7) C.(1,1) D.(2,1)
9.在平面直角坐标系中,有一条线段AB,已知点A( -3,0)和B(0,4),平移线段 AB得到线段A B .若点 A 的对应点 A 的坐标为( 则线段AB 平移经过的区域(四边形ABB A )的面积为 ( )
A.12 B.15 C.24 D.30
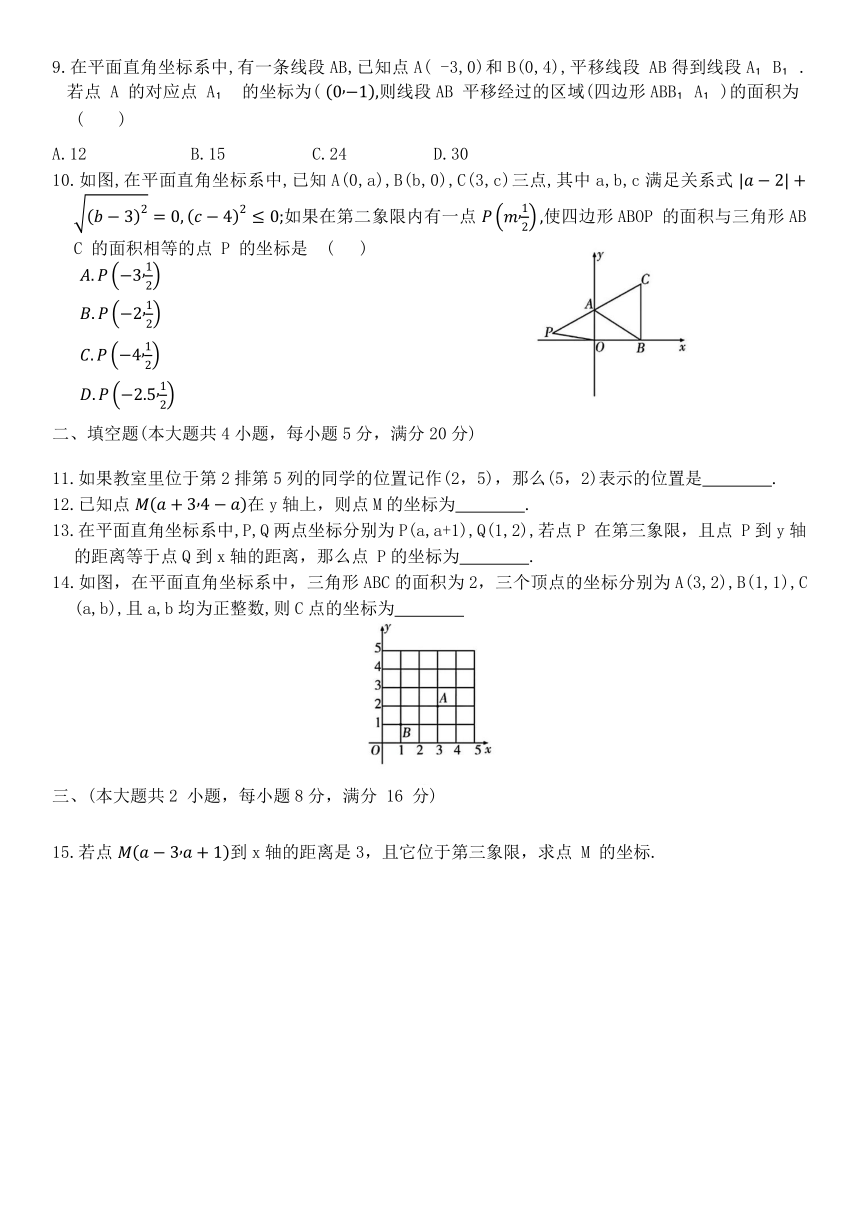
10.如图,在平面直角坐标系中,已知A(0,a),B(b,0),C(3,c)三点,其中a,b,c满足关系式 如果在第二象限内有一点 使四边形ABOP 的面积与三角形ABC 的面积相等的点 P 的坐标是 ( )
二、填空题(本大题共4小题,每小题5分,满分20分)
11.如果教室里位于第2排第5列的同学的位置记作(2,5),那么(5,2)表示的位置是 .
12.已知点 在y轴上,则点M的坐标为 .
13.在平面直角坐标系中,P,Q两点坐标分别为P(a,a+1),Q(1,2),若点P 在第三象限,且点 P到y轴的距离等于点Q到x轴的距离,那么点 P的坐标为 .
14.如图,在平面直角坐标系中,三角形ABC的面积为2,三个顶点的坐标分别为A(3,2),B(1,1),C(a,b),且a,b均为正整数,则C点的坐标为
三、(本大题共2 小题,每小题8分,满分 16 分)
15.若点 到x轴的距离是3,且它位于第三象限,求点 M 的坐标.
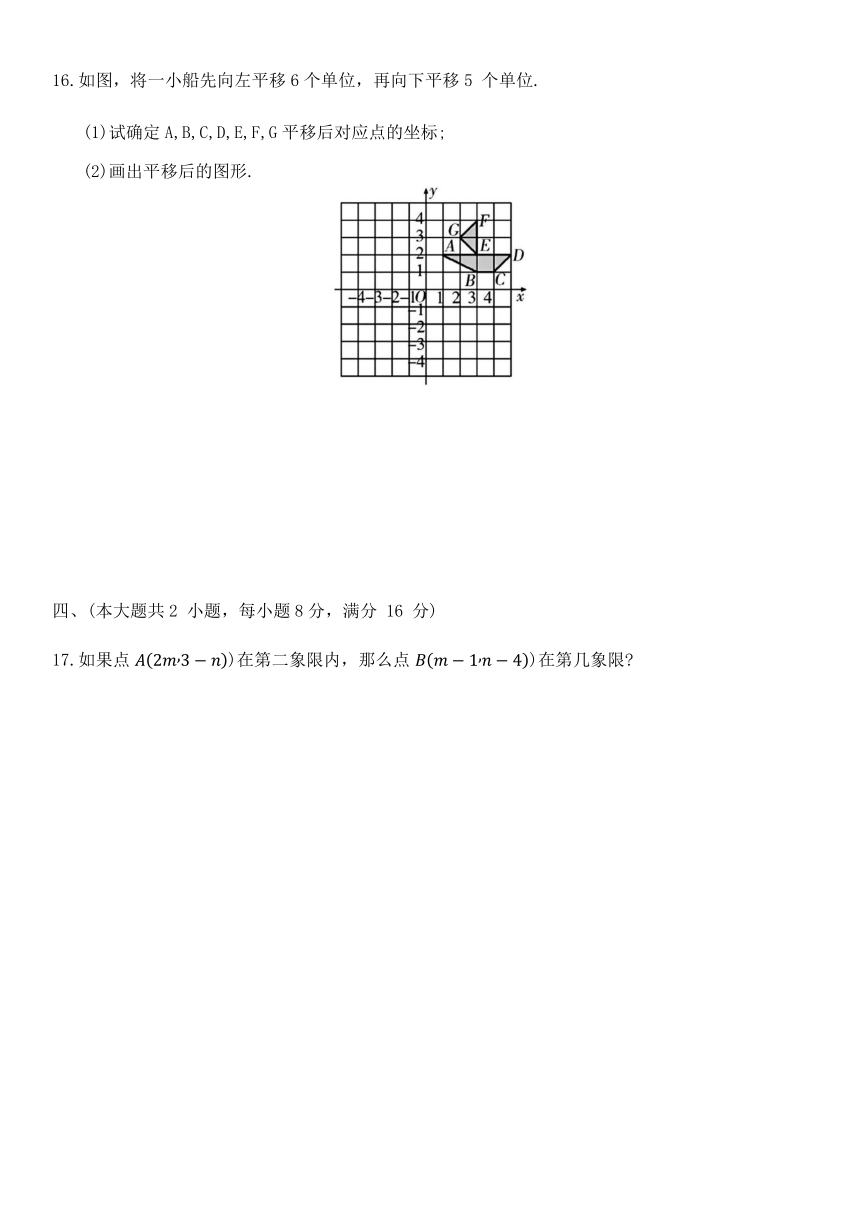
16.如图,将一小船先向左平移6个单位,再向下平移5 个单位.
(1)试确定A,B,C,D,E,F,G平移后对应点的坐标;
(2)画出平移后的图形.
四、(本大题共2 小题,每小题8分,满分 16 分)
17.如果点 )在第二象限内,那么点 )在第几象限
18.在平面直角坐标系中,一蚂蚁从原点O出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1 个单位长度,其行走路线如下图所示.
(1)写出点 和 的坐标;
(2)写出点 的坐标(n是正整数),并指出蚂蚁从点. 到点 的移动方向.
五、(本大题共2 小题,每小题10 分,满分20 分)
19.已知点 P(x,y)的坐标满足方程组 且点 P 在第四象限.
(1)请用含a的代数式表示x;
(2)请求出a的取值范围.
20.如图中的平面直角坐标系,使点B,C的坐标分别为(2,0)和(6,0),根据平面直角坐标系提供的数据,求:
(1)点A,D,E,F,G的坐标及它们所在的象限;
(2)三角形BCF及四边形ABFG的面积.
六、(本题满分12 分)
21.已知点 ,试分别根据下列条件求出点 P 的坐标.
(1)点P在y轴上;
(2)点P的纵坐标比横坐标大3;
(3)点P到x轴的距离为2,且在第四象限.
七、(本题满分12分)
22.如图是某台阶的部分示意图,各级台阶的高度与宽度相等.如果点 A的坐标为(0,0),点B的坐标为(1,1).
(1)请建立适当的平面直角坐标系,并写出点C,D,E,F的坐标;
(2)说明点 B,C,D,E,F的坐标与点A的坐标相比较有什么变化;
(3)如果台阶有10级,请你求出该台阶的高度和长度.
八、(本题满分14分)
23.如图,在平面直角坐标系中,点. 为x 轴负半轴上一点,点B(0,4b)为y轴正半轴上一点,其中b满足方程
(1)求点A,B的坐标;
(2)点C为y轴负半轴上一点,且三角形 ABC的面积为12,求点 C 的坐标;
(3)在(2)的条件下,x轴上是否存在点P,使得三角形 PBC 的面积等于三角形ABC 的面积的一半 若存在,求出相应的点 P的坐标;若不存在,请说明理由.
第 十一章 平面直角坐标系
1. C 2. B 3. C 4. C 5. B 6. B 7. D 8. C 9. B 10. A
11.第5排第2列 12.(0,7) 13.(-2,-1)
14.(5,1),(1,3),(3,4),(5,5)
15.解:根据题意,得|a+1|=3.∵点M位于第三象限,∴a+1=-3.∴a=-4.
当a=-4时,a-3=-7,∴点M的坐标为( -7,-3).
16.解:(1)由图可知,A(1,2),B(3,1),C(4,1),D(5,2),E(3,2),F(3,4),G(2,3),可确定平移后对应点的坐标分别为A'(-5,-3),B'(-3,-4),C'( -2,-4),D'(-1,-3),E'(-3,-3),F'(-3,-1),G'(-4,-2).
17.解:∵点A(2m,3-n)在第二象限内,∴ 解得m<0,n<3.
∴m-1<0,n-4<0.∴点B在第三象限内.
18.解:(1)A (0,1),A (1,0),A (6,0).
(2)当n=1时,A (2,0),当n=2时,A (4,0),当n=3时,A (6,0),所以A (2n,0).
点A100中的n正好是4的倍数,所以点A100和A101的坐标分别是A (50,0),A (50,1),所以蚂蚁从点 A100到A101的移动方向是从下向上.
19.解:(1)方程组 可整理为 (①+②)÷2,得x=2a+1.
(2)由(1)得x=2a+1,
把x=2a+1代入①,得2a+1+y-a=0,解得y=-a-1.
∵ 点 P(x,y)在第四象限,. 解得
∴a的取值范围是
20.解:(1)根据题意,建立平面直角坐标系如图.
点A的坐标为(0,3),在y轴上;
点D,E,F,G的坐标分别为(8,1),(7,3),(5,2),(3,5),在第一象限.
21.解:(1)∵点P(m+3,2m-1)在y轴上,∴m+3=0.解得m= -3.
∴2m-1=-6-1=-7.∴点P的坐标为(0,-7).
(2)∵点P的纵坐标比横坐标大3,∴(2m-1)-(m+3) =3.解得m=7.
∴m+3=7+3=10,2m-1=2×7-1=13.∴点P的坐标为(10,13).
(3)∵点P到x轴的距离为2,∴|2m﹣1|=2.解得 或
当 时, 此时,点
当 时, 此时,点
∵ 点 P在第四象限,∴点 P 的坐标为
22.解:(1)以点A为原点,水平方向为x轴,竖直方向为y轴建立平面直角坐标系,如图.
所以点C,D,E,F的坐标分别为C(2,2),D(3,3),E(4,4),F(5,5).
(2)点B,C,D,E,F的坐标与点A的坐标相比较,横坐标与纵坐标分别加1,2,3,4,5.
(3)每级台阶高为1,宽也为1,所以10级台阶的高度是10,长度为11.
23.解:(1)解方程3(b+1)=6,得b=1.∴A(-3,0),B(0,4).
(2)∵A(-3.0)∴OA=3.∵三角形ABC的面积为12.
∴OB=4.又∵点C为y轴负半轴上一点,∴OC=BC-OB=4.∴C(0,-4).
(3)存在.理由如下:
即 BC 边上的高OP 为
又∵ 点 P 在x轴上,∴ 点 P 的坐标为 或
(时间:120分钟满分:150分)
题号 一 二 三 四 五 六 七 八 总 分
得 分
一、选择题(本大题共10 小题,每小题4分,满分40 分)
1.平面直角坐标系内的下列各点中,在y轴上的点是 ( )
A.( -1,2) B.(-2,-3)
C.(0,3) D.(-3,0)
2.在平面直角坐标系中,点P 的坐标为(-3,5),则点 P 在 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
3.如图是天安门广场周围的景点分布示意图的一部分,若表示“王府井”的点的坐标为(4,1),表示“人民大会堂”的点的坐标为(0,-1),则表示“天安门”的点的坐标为 ( )
A.(0,0) B.(-1,0) C.(1,0) D.(1,1)
4.点M(-3,5)经过平移变换后得到点 N(3,5),则平移的方向和距离为( )
A.向上平移6 个单位 B.向左平移6 个单位
C.向右平移6个单位 D.向下平移6个单位
5.点P在第三象限,点P到x轴的距离是5,到y轴的距离是2,那么点P的坐标为 ( )
A.(-5,2) B.( -2,-5)
C.(-2,5) D.(2,-5)
6.已知点P( -3,-3),Q( -3,4),则直线PQ ( )
A.平行于x轴 B.平行于y轴
C.垂直于y轴 D.以上都不正确
7.无论 m取什么实数,点( 一定在 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
8.已知三角形ABC的顶点坐标分别是A(0,6),B( -3,-3),C(1,0),将三角形ABC平移后顶点A的对应点 A 的坐标是(4,10),则点 B的对应点B 的坐标为( )
A.(7,1) B.(1,7) C.(1,1) D.(2,1)
9.在平面直角坐标系中,有一条线段AB,已知点A( -3,0)和B(0,4),平移线段 AB得到线段A B .若点 A 的对应点 A 的坐标为( 则线段AB 平移经过的区域(四边形ABB A )的面积为 ( )
A.12 B.15 C.24 D.30
10.如图,在平面直角坐标系中,已知A(0,a),B(b,0),C(3,c)三点,其中a,b,c满足关系式 如果在第二象限内有一点 使四边形ABOP 的面积与三角形ABC 的面积相等的点 P 的坐标是 ( )
二、填空题(本大题共4小题,每小题5分,满分20分)
11.如果教室里位于第2排第5列的同学的位置记作(2,5),那么(5,2)表示的位置是 .
12.已知点 在y轴上,则点M的坐标为 .
13.在平面直角坐标系中,P,Q两点坐标分别为P(a,a+1),Q(1,2),若点P 在第三象限,且点 P到y轴的距离等于点Q到x轴的距离,那么点 P的坐标为 .
14.如图,在平面直角坐标系中,三角形ABC的面积为2,三个顶点的坐标分别为A(3,2),B(1,1),C(a,b),且a,b均为正整数,则C点的坐标为
三、(本大题共2 小题,每小题8分,满分 16 分)
15.若点 到x轴的距离是3,且它位于第三象限,求点 M 的坐标.
16.如图,将一小船先向左平移6个单位,再向下平移5 个单位.
(1)试确定A,B,C,D,E,F,G平移后对应点的坐标;
(2)画出平移后的图形.
四、(本大题共2 小题,每小题8分,满分 16 分)
17.如果点 )在第二象限内,那么点 )在第几象限
18.在平面直角坐标系中,一蚂蚁从原点O出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1 个单位长度,其行走路线如下图所示.
(1)写出点 和 的坐标;
(2)写出点 的坐标(n是正整数),并指出蚂蚁从点. 到点 的移动方向.
五、(本大题共2 小题,每小题10 分,满分20 分)
19.已知点 P(x,y)的坐标满足方程组 且点 P 在第四象限.
(1)请用含a的代数式表示x;
(2)请求出a的取值范围.
20.如图中的平面直角坐标系,使点B,C的坐标分别为(2,0)和(6,0),根据平面直角坐标系提供的数据,求:
(1)点A,D,E,F,G的坐标及它们所在的象限;
(2)三角形BCF及四边形ABFG的面积.
六、(本题满分12 分)
21.已知点 ,试分别根据下列条件求出点 P 的坐标.
(1)点P在y轴上;
(2)点P的纵坐标比横坐标大3;
(3)点P到x轴的距离为2,且在第四象限.
七、(本题满分12分)
22.如图是某台阶的部分示意图,各级台阶的高度与宽度相等.如果点 A的坐标为(0,0),点B的坐标为(1,1).
(1)请建立适当的平面直角坐标系,并写出点C,D,E,F的坐标;
(2)说明点 B,C,D,E,F的坐标与点A的坐标相比较有什么变化;
(3)如果台阶有10级,请你求出该台阶的高度和长度.
八、(本题满分14分)
23.如图,在平面直角坐标系中,点. 为x 轴负半轴上一点,点B(0,4b)为y轴正半轴上一点,其中b满足方程
(1)求点A,B的坐标;
(2)点C为y轴负半轴上一点,且三角形 ABC的面积为12,求点 C 的坐标;
(3)在(2)的条件下,x轴上是否存在点P,使得三角形 PBC 的面积等于三角形ABC 的面积的一半 若存在,求出相应的点 P的坐标;若不存在,请说明理由.
第 十一章 平面直角坐标系
1. C 2. B 3. C 4. C 5. B 6. B 7. D 8. C 9. B 10. A
11.第5排第2列 12.(0,7) 13.(-2,-1)
14.(5,1),(1,3),(3,4),(5,5)
15.解:根据题意,得|a+1|=3.∵点M位于第三象限,∴a+1=-3.∴a=-4.
当a=-4时,a-3=-7,∴点M的坐标为( -7,-3).
16.解:(1)由图可知,A(1,2),B(3,1),C(4,1),D(5,2),E(3,2),F(3,4),G(2,3),可确定平移后对应点的坐标分别为A'(-5,-3),B'(-3,-4),C'( -2,-4),D'(-1,-3),E'(-3,-3),F'(-3,-1),G'(-4,-2).
17.解:∵点A(2m,3-n)在第二象限内,∴ 解得m<0,n<3.
∴m-1<0,n-4<0.∴点B在第三象限内.
18.解:(1)A (0,1),A (1,0),A (6,0).
(2)当n=1时,A (2,0),当n=2时,A (4,0),当n=3时,A (6,0),所以A (2n,0).
点A100中的n正好是4的倍数,所以点A100和A101的坐标分别是A (50,0),A (50,1),所以蚂蚁从点 A100到A101的移动方向是从下向上.
19.解:(1)方程组 可整理为 (①+②)÷2,得x=2a+1.
(2)由(1)得x=2a+1,
把x=2a+1代入①,得2a+1+y-a=0,解得y=-a-1.
∵ 点 P(x,y)在第四象限,. 解得
∴a的取值范围是
20.解:(1)根据题意,建立平面直角坐标系如图.
点A的坐标为(0,3),在y轴上;
点D,E,F,G的坐标分别为(8,1),(7,3),(5,2),(3,5),在第一象限.
21.解:(1)∵点P(m+3,2m-1)在y轴上,∴m+3=0.解得m= -3.
∴2m-1=-6-1=-7.∴点P的坐标为(0,-7).
(2)∵点P的纵坐标比横坐标大3,∴(2m-1)-(m+3) =3.解得m=7.
∴m+3=7+3=10,2m-1=2×7-1=13.∴点P的坐标为(10,13).
(3)∵点P到x轴的距离为2,∴|2m﹣1|=2.解得 或
当 时, 此时,点
当 时, 此时,点
∵ 点 P在第四象限,∴点 P 的坐标为
22.解:(1)以点A为原点,水平方向为x轴,竖直方向为y轴建立平面直角坐标系,如图.
所以点C,D,E,F的坐标分别为C(2,2),D(3,3),E(4,4),F(5,5).
(2)点B,C,D,E,F的坐标与点A的坐标相比较,横坐标与纵坐标分别加1,2,3,4,5.
(3)每级台阶高为1,宽也为1,所以10级台阶的高度是10,长度为11.
23.解:(1)解方程3(b+1)=6,得b=1.∴A(-3,0),B(0,4).
(2)∵A(-3.0)∴OA=3.∵三角形ABC的面积为12.
∴OB=4.又∵点C为y轴负半轴上一点,∴OC=BC-OB=4.∴C(0,-4).
(3)存在.理由如下:
即 BC 边上的高OP 为
又∵ 点 P 在x轴上,∴ 点 P 的坐标为 或
