沪科版数学八年级上册 第十二章 一次函数 单元测试(含答案)
文档属性
| 名称 | 沪科版数学八年级上册 第十二章 一次函数 单元测试(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 747.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-06 00:00:00 | ||
图片预览




文档简介
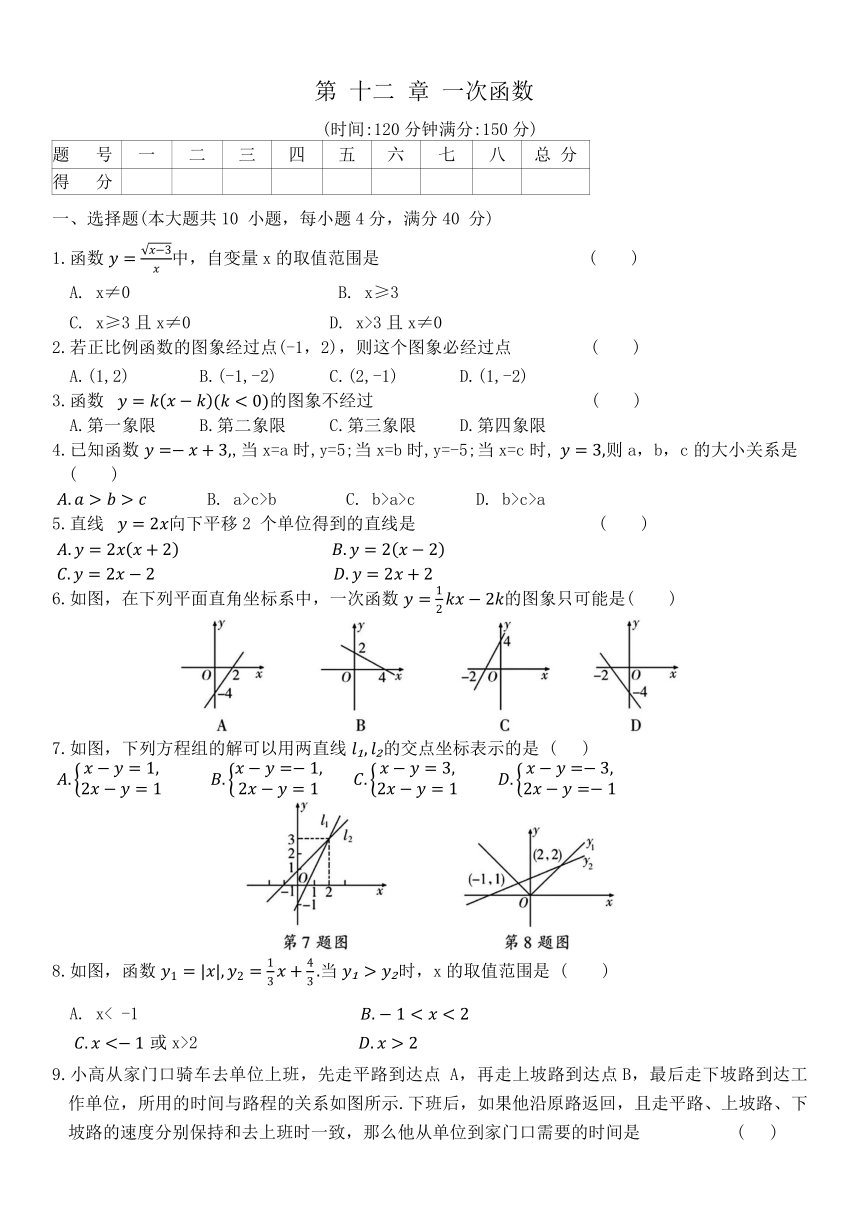
第 十二 章 一次函数
(时间:120分钟满分:150分)
题 号 一 二 三 四 五 六 七 八 总 分
得 分
一、选择题(本大题共10 小题,每小题4分,满分40 分)
1.函数 中,自变量x的取值范围是 ( )
A. x≠0 B. x≥3
C. x≥3且x≠0 D. x>3且x≠0
2.若正比例函数的图象经过点(-1,2),则这个图象必经过点 ( )
A.(1,2) B.(-1,-2) C.(2,-1) D.(1,-2)
3.函数 的图象不经过 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.已知函数 ,当x=a时,y=5;当x=b时,y=-5;当x=c时, 则a,b,c的大小关系是 ( )
B. a>c>b C. b>a>c D. b>c>a
5.直线 向下平移2 个单位得到的直线是 ( )
6.如图,在下列平面直角坐标系中,一次函数 的图象只可能是( )
7.如图,下列方程组的解可以用两直线 的交点坐标表示的是 ( )
8.如图,函数 当 时,x的取值范围是 ( )
A. x< -1
或x>2
9.小高从家门口骑车去单位上班,先走平路到达点 A,再走上坡路到达点B,最后走下坡路到达工作单位,所用的时间与路程的关系如图所示.下班后,如果他沿原路返回,且走平路、上坡路、下坡路的速度分别保持和去上班时一致,那么他从单位到家门口需要的时间是 ( )
A.12 分钟 B.15分钟 C.25分钟 D.27 分钟
10.如图,在平面直角坐标系中,在边长为1 的正方形ABCD 的边上有一动点 P 沿A→B→C→D→A运动一周,则点 P的纵坐标y与点 P 走过的路程s之间的函数关系用图象表示大致是 ( )
二、填空题(本大题共4 小题,每小题5分,满分20分)
11.已知一次函数 ,当m满足 时,直线在y轴上的截距小于0.
12.一次函数 的函数值为0,则
13.甲、乙两人以相同路线前往距离单位10 千米的培训中心参加学习.图中 分别表示甲、乙两人前往目的地所走的路程s(千米)随时间t(分)变化的函数图象.以下说法:
①乙比甲提前12分钟到达;
②甲的平均速度为15千米/时;
③乙的平均速度为 千米/时;
④乙出发6分钟后追上甲.
其中正确的有 .(填所有正确的序号)
14.已知一次函数 (a,b是常数),x与y的部分对应值如下表:
x -2 -1 0 1 2 3
y 6 4 2 0 -2 -4
那么方程ax+b=0的解是 ;不等式。ax+b>0的解集是 .
三、(本大题共2 小题,每小题8分,满分 16 分)
15.已知函数 当m,n为何值时,此函数是一次函数 当m,n为何值时,此函数是正比例函数
16.在平面直角坐标系中解答下列问题:
(1)画出函数 的图象并写出图象与x轴的交点A 的坐标;
(2)在(1)的条件下,平面内有一点 当 的面积是6时,求b的值.
四、(本大题共2 小题,每小题8分,满分16 分)
17.已知 与 成正比例,且当 时,
(1)求y与x之间的函数表达式;
(2)当 时,求x的值.
18.如图,设函数 的图象与y轴交于点A,函数 的图象与y轴交于点B,两个函数的图象交于点C,求通过线段AB 的中点 D 及点 C 的直线的一次函数表达式.
五、(本大题共2 小题,每小题10分,满分20 分)
19.某校运动会需购买A,B两种奖品共100件,A,B 两种奖品每件的价格分别为10元、15 元.设购买A种奖品m件,购买两种奖品的总费用为W元.
(1)写出 W与m之间的函数表达式;
(2)若购买两种奖品的总费用不超过1150元,且A 种奖品的数量不大于 B种奖品数量的3倍,求出自变量m的取值范围,并确定最少费用W的值.
20.如图,在平面直角坐标系中,过点. 的直线 与直线 相交于点 B(m,4).
(1)求直线 的表达式;
(2)过动点P(n,0)且垂直x轴的直线与 的交点分别为C,D,当点C 位于点 D上方时,写出n的取值范围.
六、(本题满分12分)
21.甲、乙两辆汽车同时从相距280km的A,B两地相向而行,s(km)表示汽车与A 地的距离,t(min)表示汽车行驶的时间.如图, 分别表示两辆汽车的s与t的关系.
(1)汽车乙的速度是多少
(2)1小时后,甲、乙两辆汽车相距多少千米
(3)行驶多长时间,甲、乙两辆汽车相遇
七、(本题满分12分)
22.某文具商店销售功能相同的A,B两种品牌的计算器,购买2个 A 品牌和3个B品牌的计算器共需156元;购买3个A品牌和1个B品牌的计算器共需 122 元.
(1)求这两种品牌计算器的单价;
(2)学校开学前夕,该商店对这两种计算器开展了促销活动,具体办法如下:A品牌计算器按原价的八折销售,B 品牌计算器5 个以上超出部分按原价的七折销售.设购买x个A品牌的计算器需要y 元,购 买x个B品牌的计算器需要y 元,分别求出y ,y 关于x的函数表 达式;
(3)小明准备联系一部分同学集体购买同一品牌的计算器,若购买计算器的数量超过5个,购买哪种品牌的计算器更合算 请说明理由.
八、(本题满分14分)
23.如图,直线 与x轴正半轴、y轴负半轴分别交于B,C 两点,且
(1)求点 B 的坐标和k的值;
(2)若点A是直线 上的一个动点(不与点B 重合),且点 A 的横坐标为t,试写出在点A 运动过程中,三角形AOB的面积S与t之间的函数表达式;
(3)若三角形AOB的面积为1,试确定点A的坐标.
第十二 章 一次函数
1. B 2. D 3. A 4. D 5. C 6. B 7. B 8. C 9. B 10. D
11. m>-1且 12.3 13.①②④ 14. x=1 x<1
15.解:根据一次函数的定义,得2-|m|=1,且m+1≠0,解得m=1.
∴当m=1,n为任意数时,此函数是一次函数.
根据正比例函数的定义,得2-|m|=1,n+4=0,且m+1≠0,解得m=1,n= -4.∴当m=1,n=-4时,此函数是正比例函数.
16.解:(1)当x=0时,y=4,当y=0时,x=-2,画出函数的图象如图.
根据图象可知,函数与x轴的交点A的坐标为(-2,0).
(2)由(1)可知点A的坐标为( -2,0),∴OA=2.
∵ 点 B的坐标为
17.解:(1)∵y+2与x-1成正比例,设y+2=k(x-1).
将x=3,y=4代入上式,得4+2=k(3-1).解得k=3.
∴y与x之间的函数表达式为y+2=3(x-1),即y=3x-5.
(2)将y=1代入y=3x-5,得1=3x-5.解得x=2.即当y=1时,x=2.
18.解:由题意可知,y=x+4与y轴的交点坐标为A(0,4),y= -3x-6与y轴的交点坐标为B(0,-6),所以A,B的中点坐标为D(0,-1).
联立 解得 所以点 C 的坐标为
设直线 CD的函数表达式为y=kx+b,则有 解得
所以过点C,D的直线的表达式为y=-x-1.
19.解:(1)根据题意,知A,B两种奖品共购买100件,
则购买B种奖品(100-m)件,则W=10m+15(100-m)=-5m+1500.
所以 W与m之间的函数表达式为W=-5m+1 500(0≤m≤100).
(2)根据题意,得 解得70≤m≤75.
∵ -5<0,∴W随m的增大而减小.
∴当m=75时,W取最小值,W最小=-5×75+1500=1125.
∴ 自变量的取值范围是70≤m≤75,最小费用是1 125元.
20.解:(1)∵点B在直线l 上,∴4=2m.∴m=2.
设l 的表达式为y=kx+b.
由A,B两点均在直线l 上,得 解得 则直线l 的表达式为
(2)根据题意,得点 C的坐标为 点 D 的坐标为(n,2n).
∵ 点 C 在点 D 的上方,. 解得n<2.∴n的取值范围为n<2.
21.解:(1)60分=1时,汽车乙的速度为(280-200)÷1=80(千米/时).
(2)由图可得l 经过(0,280),(60,200),l 经过(0,0),(60,60),
设l 的表达式为. 的表达式为
则 解得
∴l 的表达式为 的表达式为s甲 =t.
∴当t=60时,s乙=-80+280=200,s =60.
(千米).∴1小时后,甲、乙两辆汽车相距140千米.
(3)根据题意,得 解得
∴120分=2时,即行驶2 小时两车相遇.
22.解:(1)设A品牌计算器的单价为x元/个,B品牌计算器的单价为y元/个.
根据题意,得 解得
即A,B两种品牌计算器的单价分别为30 元/个和32 元/个.
(2)根据题意,得y =0.8×30x,即.
当0≤x≤5时,y =32x;
当x>5时,y =32×5+32(x-5)×0.7,即.
∴y 关于x的函数表达式为y =24x,y 关于x的函数表达式为
(3)当购买数量超过5个时,
当 时,24x<22.4x+48,解得x<30.
当 时,24x=22.4x+48,解得x=30.
当 时,24x>22.4x+48,解得x>30.
故当购买数量超过5个而不足30个时,购买A品牌的计算器更合算;当购买数量为30个时,购买A品牌与B品牌的计算器花费相同;当购买数量超过30个时,购买 B品牌的计算器更合算.
23.解:(1)∵y=kx-1与y轴相交于点C,∴OC=1.
∵OC=20B,∴OB=0.5.∴点B的坐标为(0.5,0).
把x=0.5,y=0代入y=kx-1,解得k=2.∴k的值为2.
(2)如图,过点A作AD⊥x轴于点D,
∵k=2,∴直线BC的表达式为y=2x-1.
当t>0.5时,AD=2t-1,
∴S与t之间的函数表达式为
0.25.
当t<0.5时,AD=1 -2t,
∴S与t之间的函数表达式为
∴S与t之间的函数表达式为
(3)当0.5t-0.25=1时,解得t=2.5,则2t-1=4.当--0.5t+0.25=1时,解得t= -1.5,则2t-1= -4.故点A的坐标为(2.5,4)或( -1.5,-4).
(时间:120分钟满分:150分)
题 号 一 二 三 四 五 六 七 八 总 分
得 分
一、选择题(本大题共10 小题,每小题4分,满分40 分)
1.函数 中,自变量x的取值范围是 ( )
A. x≠0 B. x≥3
C. x≥3且x≠0 D. x>3且x≠0
2.若正比例函数的图象经过点(-1,2),则这个图象必经过点 ( )
A.(1,2) B.(-1,-2) C.(2,-1) D.(1,-2)
3.函数 的图象不经过 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.已知函数 ,当x=a时,y=5;当x=b时,y=-5;当x=c时, 则a,b,c的大小关系是 ( )
B. a>c>b C. b>a>c D. b>c>a
5.直线 向下平移2 个单位得到的直线是 ( )
6.如图,在下列平面直角坐标系中,一次函数 的图象只可能是( )
7.如图,下列方程组的解可以用两直线 的交点坐标表示的是 ( )
8.如图,函数 当 时,x的取值范围是 ( )
A. x< -1
或x>2
9.小高从家门口骑车去单位上班,先走平路到达点 A,再走上坡路到达点B,最后走下坡路到达工作单位,所用的时间与路程的关系如图所示.下班后,如果他沿原路返回,且走平路、上坡路、下坡路的速度分别保持和去上班时一致,那么他从单位到家门口需要的时间是 ( )
A.12 分钟 B.15分钟 C.25分钟 D.27 分钟
10.如图,在平面直角坐标系中,在边长为1 的正方形ABCD 的边上有一动点 P 沿A→B→C→D→A运动一周,则点 P的纵坐标y与点 P 走过的路程s之间的函数关系用图象表示大致是 ( )
二、填空题(本大题共4 小题,每小题5分,满分20分)
11.已知一次函数 ,当m满足 时,直线在y轴上的截距小于0.
12.一次函数 的函数值为0,则
13.甲、乙两人以相同路线前往距离单位10 千米的培训中心参加学习.图中 分别表示甲、乙两人前往目的地所走的路程s(千米)随时间t(分)变化的函数图象.以下说法:
①乙比甲提前12分钟到达;
②甲的平均速度为15千米/时;
③乙的平均速度为 千米/时;
④乙出发6分钟后追上甲.
其中正确的有 .(填所有正确的序号)
14.已知一次函数 (a,b是常数),x与y的部分对应值如下表:
x -2 -1 0 1 2 3
y 6 4 2 0 -2 -4
那么方程ax+b=0的解是 ;不等式。ax+b>0的解集是 .
三、(本大题共2 小题,每小题8分,满分 16 分)
15.已知函数 当m,n为何值时,此函数是一次函数 当m,n为何值时,此函数是正比例函数
16.在平面直角坐标系中解答下列问题:
(1)画出函数 的图象并写出图象与x轴的交点A 的坐标;
(2)在(1)的条件下,平面内有一点 当 的面积是6时,求b的值.
四、(本大题共2 小题,每小题8分,满分16 分)
17.已知 与 成正比例,且当 时,
(1)求y与x之间的函数表达式;
(2)当 时,求x的值.
18.如图,设函数 的图象与y轴交于点A,函数 的图象与y轴交于点B,两个函数的图象交于点C,求通过线段AB 的中点 D 及点 C 的直线的一次函数表达式.
五、(本大题共2 小题,每小题10分,满分20 分)
19.某校运动会需购买A,B两种奖品共100件,A,B 两种奖品每件的价格分别为10元、15 元.设购买A种奖品m件,购买两种奖品的总费用为W元.
(1)写出 W与m之间的函数表达式;
(2)若购买两种奖品的总费用不超过1150元,且A 种奖品的数量不大于 B种奖品数量的3倍,求出自变量m的取值范围,并确定最少费用W的值.
20.如图,在平面直角坐标系中,过点. 的直线 与直线 相交于点 B(m,4).
(1)求直线 的表达式;
(2)过动点P(n,0)且垂直x轴的直线与 的交点分别为C,D,当点C 位于点 D上方时,写出n的取值范围.
六、(本题满分12分)
21.甲、乙两辆汽车同时从相距280km的A,B两地相向而行,s(km)表示汽车与A 地的距离,t(min)表示汽车行驶的时间.如图, 分别表示两辆汽车的s与t的关系.
(1)汽车乙的速度是多少
(2)1小时后,甲、乙两辆汽车相距多少千米
(3)行驶多长时间,甲、乙两辆汽车相遇
七、(本题满分12分)
22.某文具商店销售功能相同的A,B两种品牌的计算器,购买2个 A 品牌和3个B品牌的计算器共需156元;购买3个A品牌和1个B品牌的计算器共需 122 元.
(1)求这两种品牌计算器的单价;
(2)学校开学前夕,该商店对这两种计算器开展了促销活动,具体办法如下:A品牌计算器按原价的八折销售,B 品牌计算器5 个以上超出部分按原价的七折销售.设购买x个A品牌的计算器需要y 元,购 买x个B品牌的计算器需要y 元,分别求出y ,y 关于x的函数表 达式;
(3)小明准备联系一部分同学集体购买同一品牌的计算器,若购买计算器的数量超过5个,购买哪种品牌的计算器更合算 请说明理由.
八、(本题满分14分)
23.如图,直线 与x轴正半轴、y轴负半轴分别交于B,C 两点,且
(1)求点 B 的坐标和k的值;
(2)若点A是直线 上的一个动点(不与点B 重合),且点 A 的横坐标为t,试写出在点A 运动过程中,三角形AOB的面积S与t之间的函数表达式;
(3)若三角形AOB的面积为1,试确定点A的坐标.
第十二 章 一次函数
1. B 2. D 3. A 4. D 5. C 6. B 7. B 8. C 9. B 10. D
11. m>-1且 12.3 13.①②④ 14. x=1 x<1
15.解:根据一次函数的定义,得2-|m|=1,且m+1≠0,解得m=1.
∴当m=1,n为任意数时,此函数是一次函数.
根据正比例函数的定义,得2-|m|=1,n+4=0,且m+1≠0,解得m=1,n= -4.∴当m=1,n=-4时,此函数是正比例函数.
16.解:(1)当x=0时,y=4,当y=0时,x=-2,画出函数的图象如图.
根据图象可知,函数与x轴的交点A的坐标为(-2,0).
(2)由(1)可知点A的坐标为( -2,0),∴OA=2.
∵ 点 B的坐标为
17.解:(1)∵y+2与x-1成正比例,设y+2=k(x-1).
将x=3,y=4代入上式,得4+2=k(3-1).解得k=3.
∴y与x之间的函数表达式为y+2=3(x-1),即y=3x-5.
(2)将y=1代入y=3x-5,得1=3x-5.解得x=2.即当y=1时,x=2.
18.解:由题意可知,y=x+4与y轴的交点坐标为A(0,4),y= -3x-6与y轴的交点坐标为B(0,-6),所以A,B的中点坐标为D(0,-1).
联立 解得 所以点 C 的坐标为
设直线 CD的函数表达式为y=kx+b,则有 解得
所以过点C,D的直线的表达式为y=-x-1.
19.解:(1)根据题意,知A,B两种奖品共购买100件,
则购买B种奖品(100-m)件,则W=10m+15(100-m)=-5m+1500.
所以 W与m之间的函数表达式为W=-5m+1 500(0≤m≤100).
(2)根据题意,得 解得70≤m≤75.
∵ -5<0,∴W随m的增大而减小.
∴当m=75时,W取最小值,W最小=-5×75+1500=1125.
∴ 自变量的取值范围是70≤m≤75,最小费用是1 125元.
20.解:(1)∵点B在直线l 上,∴4=2m.∴m=2.
设l 的表达式为y=kx+b.
由A,B两点均在直线l 上,得 解得 则直线l 的表达式为
(2)根据题意,得点 C的坐标为 点 D 的坐标为(n,2n).
∵ 点 C 在点 D 的上方,. 解得n<2.∴n的取值范围为n<2.
21.解:(1)60分=1时,汽车乙的速度为(280-200)÷1=80(千米/时).
(2)由图可得l 经过(0,280),(60,200),l 经过(0,0),(60,60),
设l 的表达式为. 的表达式为
则 解得
∴l 的表达式为 的表达式为s甲 =t.
∴当t=60时,s乙=-80+280=200,s =60.
(千米).∴1小时后,甲、乙两辆汽车相距140千米.
(3)根据题意,得 解得
∴120分=2时,即行驶2 小时两车相遇.
22.解:(1)设A品牌计算器的单价为x元/个,B品牌计算器的单价为y元/个.
根据题意,得 解得
即A,B两种品牌计算器的单价分别为30 元/个和32 元/个.
(2)根据题意,得y =0.8×30x,即.
当0≤x≤5时,y =32x;
当x>5时,y =32×5+32(x-5)×0.7,即.
∴y 关于x的函数表达式为y =24x,y 关于x的函数表达式为
(3)当购买数量超过5个时,
当 时,24x<22.4x+48,解得x<30.
当 时,24x=22.4x+48,解得x=30.
当 时,24x>22.4x+48,解得x>30.
故当购买数量超过5个而不足30个时,购买A品牌的计算器更合算;当购买数量为30个时,购买A品牌与B品牌的计算器花费相同;当购买数量超过30个时,购买 B品牌的计算器更合算.
23.解:(1)∵y=kx-1与y轴相交于点C,∴OC=1.
∵OC=20B,∴OB=0.5.∴点B的坐标为(0.5,0).
把x=0.5,y=0代入y=kx-1,解得k=2.∴k的值为2.
(2)如图,过点A作AD⊥x轴于点D,
∵k=2,∴直线BC的表达式为y=2x-1.
当t>0.5时,AD=2t-1,
∴S与t之间的函数表达式为
0.25.
当t<0.5时,AD=1 -2t,
∴S与t之间的函数表达式为
∴S与t之间的函数表达式为
(3)当0.5t-0.25=1时,解得t=2.5,则2t-1=4.当--0.5t+0.25=1时,解得t= -1.5,则2t-1= -4.故点A的坐标为(2.5,4)或( -1.5,-4).
