6.2.1 向量基本定理(含答案)高一数学人教B版(2019)必修第二册课时优化训练
文档属性
| 名称 | 6.2.1 向量基本定理(含答案)高一数学人教B版(2019)必修第二册课时优化训练 |

|
|
| 格式 | docx | ||
| 文件大小 | 368.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-06 22:26:37 | ||
图片预览


文档简介
6.2.1 向量基本定理
——高一数学人教B版(2019)必修第二册课时优化训练
1.在中,,,点D满足,若为一组基底,则( )
A. B. C. D.
2.设,可以构成平面的一组基底,则下面四组向量中,不能构成基底的是( )
A.和 B.和
C.和 D.和
3.在中,M为边BC上任意一点,N为AM的中点,,则的值为( )
A. B. C. D.1
4.在直角梯形ABCD中,角B为直角,,,若,则( )
A. B. C.1 D.2
5.已知非零向量,不共线,如果,,,那么A,B,C,D四点( )
A.一定共线 B.恰是空间四边形的四个顶点
C.一定共面 D.一定不共面
6.在中,P是BC边的中点,,,的对边分别是a,b,c,若,则为( )
A.直角三角形 B.钝角三角形 C.等边三角形 D.等腰三角形
7.若点G是所在平面上一点,且,H是直线BG上一点,,则的最小值是( )
A.2 B.1 C. D.
8.已知中,,,,点D在BC边上,且,则线段AD的长度为( )
A. B. C. D.
9.(多选)下列结论正确的是( )
A.一个平面内只有一对不共线的向量可组成表示该平面内所有向量的一组基底
B.若(,,是单位向量),则,
C.向量a与b共线存在不全为零的实数,,使
D.已知A,B,P三点共线,O为该直线外任意一点,若,则
10.(多选)如图,在中,,,与BE交于点F,则下列说法正确的是( )
A. B.
C. D.
11.设向量,,,试用m,n表示p,则_________.
12.设D为所在平面内一点,.若,则__________.
13.设,是不共线向量,与共线,则实数k的值为__________.
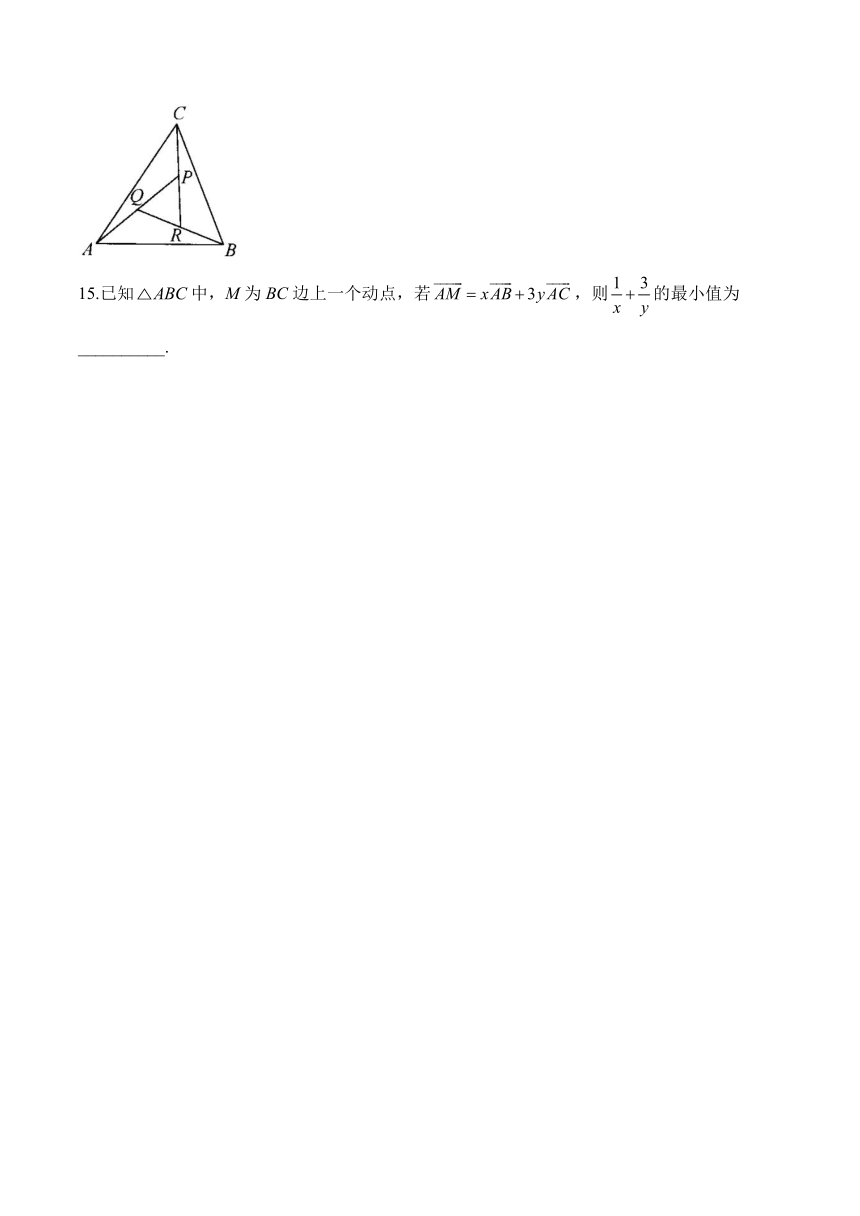
14.如图,在中,设,,的中点为Q,BQ的中点为R,CR的中点为P.若,则的值为___________.
15.已知中,M为BC边上一个动点,若,则的最小值为__________.
答案以及解析
1.答案:A
解析:,,,,故选A.
2.答案:C
解析:因为,可以构成平面的一组基底,所以,不共线,
若两个向量不能构成基底,则两向量共线,结合选项知选C.
3.答案:A
解析:因为M为边BC上任意一点,所以可设.因为N为AM的中点,所以,从而有.
4.答案:B
解析:因为,,所以,可得,即,又,所以.故选B.
5.答案:C
解析:,由平面向量基本定理可知,A,B,C,D四点共面.故选C.
6.答案:C
解析:是BC边的中点,.
,,即.
与不共线,且,,
是等边三角形.故选C.
7.答案:C
解析:因为,所以点G是的重心,设点D是AC的中点,则,连接BD,B,G,D三点共线,如图,.
因为B,H,D三点共线,
所以,
从而有,当且仅当,即,时取等号,即的最小值是.故选C.
8.答案:D
解析:由题意得,
因为,,,
所以
,即线段AD的长度为.故选D.
9.答案:CD
解析:对于A,由平面向量基底的概念可知,只要不共线的任何两个向量都可以组成平面的一组基底,故A错误;
对于B,不妨设,,,此时有,但,不成立,故B错误;
对于C,由平面向量基本定理可知C正确;
对于D,由平面向量基本定理可知,其中,,若,则,故D正确.故选CD.
10.答案:BCD
解析:,故A错误;
因为B,F,E三点共线,所以存在实数使得,
因为A,F,D三点共线,所以存在实数使得,从而有解得即,所以F为BE的中点,从而有,故B正确;
,,
所以,故C正确;取AB的中点G,BC的中点H,连接GH,如图,则G,F,H三点共线,
所以
,故D正确.故选BCD.
11.答案:
解析:设,则,得解得所以.
12.答案:-3
解析:因为,所以,即,又,所以,解得.
13.答案:
解析:与共线,则存在实数,使得,
又,是不共线向量,所以得.
14.答案:
解析:由题意可得,.因为,①
,②
所以联立①②解得.又,可得,,所以.
15.答案:16
解析:由题意得M,B,C三点共线,所以,使得,所以,整理得.
又,,不共线,所以则有.
显然,,所以,
当且仅当,即时等号成立.
故的最小值为16.
——高一数学人教B版(2019)必修第二册课时优化训练
1.在中,,,点D满足,若为一组基底,则( )
A. B. C. D.
2.设,可以构成平面的一组基底,则下面四组向量中,不能构成基底的是( )
A.和 B.和
C.和 D.和
3.在中,M为边BC上任意一点,N为AM的中点,,则的值为( )
A. B. C. D.1
4.在直角梯形ABCD中,角B为直角,,,若,则( )
A. B. C.1 D.2
5.已知非零向量,不共线,如果,,,那么A,B,C,D四点( )
A.一定共线 B.恰是空间四边形的四个顶点
C.一定共面 D.一定不共面
6.在中,P是BC边的中点,,,的对边分别是a,b,c,若,则为( )
A.直角三角形 B.钝角三角形 C.等边三角形 D.等腰三角形
7.若点G是所在平面上一点,且,H是直线BG上一点,,则的最小值是( )
A.2 B.1 C. D.
8.已知中,,,,点D在BC边上,且,则线段AD的长度为( )
A. B. C. D.
9.(多选)下列结论正确的是( )
A.一个平面内只有一对不共线的向量可组成表示该平面内所有向量的一组基底
B.若(,,是单位向量),则,
C.向量a与b共线存在不全为零的实数,,使
D.已知A,B,P三点共线,O为该直线外任意一点,若,则
10.(多选)如图,在中,,,与BE交于点F,则下列说法正确的是( )
A. B.
C. D.
11.设向量,,,试用m,n表示p,则_________.
12.设D为所在平面内一点,.若,则__________.
13.设,是不共线向量,与共线,则实数k的值为__________.
14.如图,在中,设,,的中点为Q,BQ的中点为R,CR的中点为P.若,则的值为___________.
15.已知中,M为BC边上一个动点,若,则的最小值为__________.
答案以及解析
1.答案:A
解析:,,,,故选A.
2.答案:C
解析:因为,可以构成平面的一组基底,所以,不共线,
若两个向量不能构成基底,则两向量共线,结合选项知选C.
3.答案:A
解析:因为M为边BC上任意一点,所以可设.因为N为AM的中点,所以,从而有.
4.答案:B
解析:因为,,所以,可得,即,又,所以.故选B.
5.答案:C
解析:,由平面向量基本定理可知,A,B,C,D四点共面.故选C.
6.答案:C
解析:是BC边的中点,.
,,即.
与不共线,且,,
是等边三角形.故选C.
7.答案:C
解析:因为,所以点G是的重心,设点D是AC的中点,则,连接BD,B,G,D三点共线,如图,.
因为B,H,D三点共线,
所以,
从而有,当且仅当,即,时取等号,即的最小值是.故选C.
8.答案:D
解析:由题意得,
因为,,,
所以
,即线段AD的长度为.故选D.
9.答案:CD
解析:对于A,由平面向量基底的概念可知,只要不共线的任何两个向量都可以组成平面的一组基底,故A错误;
对于B,不妨设,,,此时有,但,不成立,故B错误;
对于C,由平面向量基本定理可知C正确;
对于D,由平面向量基本定理可知,其中,,若,则,故D正确.故选CD.
10.答案:BCD
解析:,故A错误;
因为B,F,E三点共线,所以存在实数使得,
因为A,F,D三点共线,所以存在实数使得,从而有解得即,所以F为BE的中点,从而有,故B正确;
,,
所以,故C正确;取AB的中点G,BC的中点H,连接GH,如图,则G,F,H三点共线,
所以
,故D正确.故选BCD.
11.答案:
解析:设,则,得解得所以.
12.答案:-3
解析:因为,所以,即,又,所以,解得.
13.答案:
解析:与共线,则存在实数,使得,
又,是不共线向量,所以得.
14.答案:
解析:由题意可得,.因为,①
,②
所以联立①②解得.又,可得,,所以.
15.答案:16
解析:由题意得M,B,C三点共线,所以,使得,所以,整理得.
又,,不共线,所以则有.
显然,,所以,
当且仅当,即时等号成立.
故的最小值为16.
