八年级数学上册苏科版 第3章《勾股定理》综合测试卷 (含答案)
文档属性
| 名称 | 八年级数学上册苏科版 第3章《勾股定理》综合测试卷 (含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 958.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-06 22:57:10 | ||
图片预览


文档简介
第3章《勾股定理》综合测试卷
一、选择题(本大题共10小题,每小题2分,共20分)
1.下列三条线段能组成直角三角形的是( )
A. B.
C. D.
2.如图,在边长为1个单位长度的小正方形组成的网格中,点A,B都是格点,则线段AB的长度为( )
A.5 B.6 C.7 D.9
3.下列说法正确的是( )
A.若,,是的三边,则
B.若,,是的三边,则
C.若,,是的三边,,则
D.若,,是的三边,,则
4.如图是一个圆柱形饮料罐,底面半径是3,高是4,上底面中心有一个小圆孔,则一条长10cm的直吸管露在罐外部分的长度(罐壁的厚度和小圆孔的大小忽略不计)范围是( )
A. B. C. D.
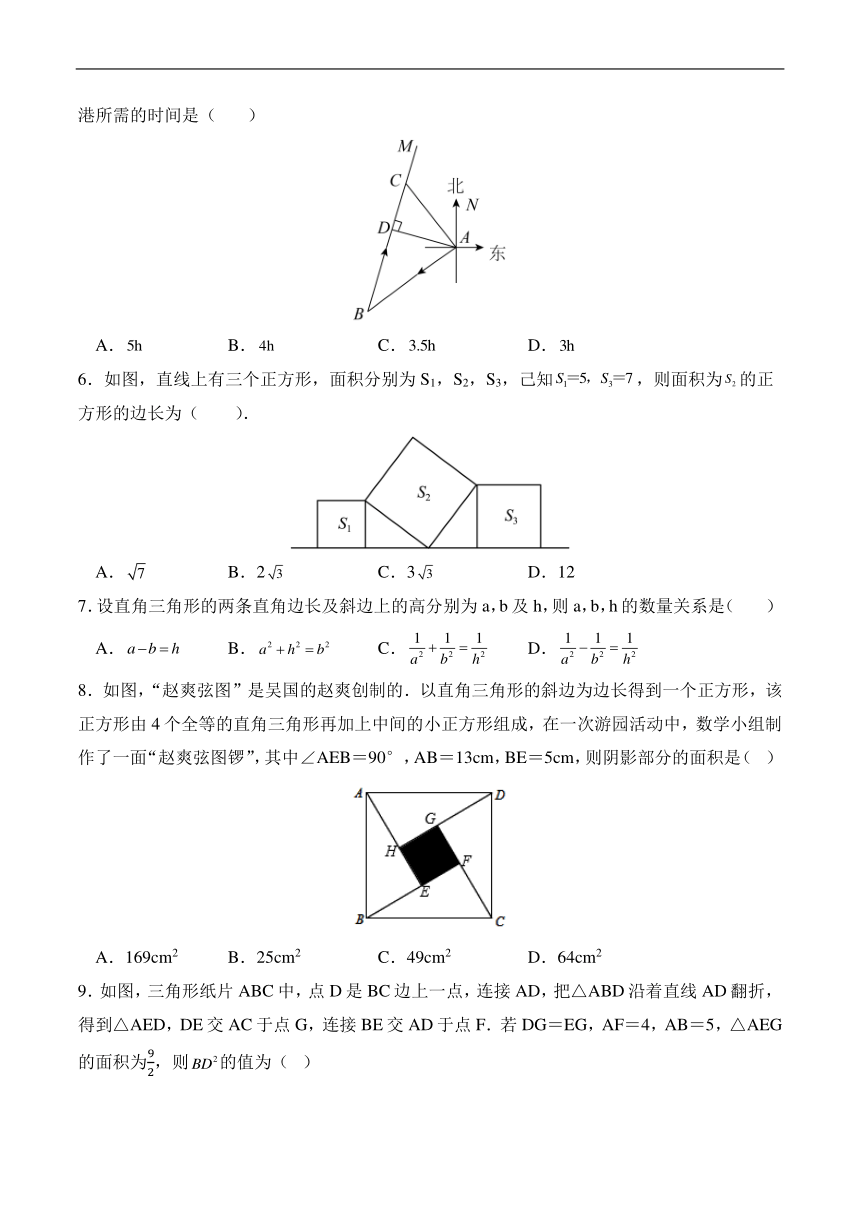
5.一艘轮船从A港向南偏西方向航行到达B岛,再从B岛沿方向航行到达C岛,A港到航线的最短距离是.若轮船速度为,轮船从C岛沿返回A港所需的时间是( )
A. B. C. D.
6.如图,直线上有三个正方形,面积分别为S1,S2,S3,己知,则面积为的正方形的边长为( ).
A. B.2 C.3 D.12
7.设直角三角形的两条直角边长及斜边上的高分别为a,b及h,则a,b,h的数量关系是( )
A. B. C. D.
8.如图,“赵爽弦图”是吴国的赵爽创制的.以直角三角形的斜边为边长得到一个正方形,该正方形由4个全等的直角三角形再加上中间的小正方形组成,在一次游园活动中,数学小组制作了一面“赵爽弦图锣”,其中∠AEB=90°,AB=13cm,BE=5cm,则阴影部分的面积是( )
A.169cm2 B.25cm2 C.49cm2 D.64cm2
9.如图,三角形纸片ABC中,点D是BC边上一点,连接AD,把△ABD沿着直线AD翻折,得到△AED,DE交AC于点G,连接BE交AD于点F.若DG=EG,AF=4,AB=5,△AEG的面积为,则的值为( )
A.13 B.12 C.11 D.10
10.中国古代称直角三角形为勾股形,如果勾股形的三边长为三个正整数,则称三边长叫“勾股数”;如果勾股形的两直角边长为正整数,那么称斜边长的平方叫“整弦数”对于以下结论:①20是“整弦数”;②两个“整弦数”之和一定是“整弦数”;③若c2为“整弦数”,则c不可能为正整数;④若m=a12+b12,n=a22+b22,≠,且m,n,a1,a2,b1,b2均为正整数,则m与n之积为“整弦数”;⑤若一个正奇数(除1外)的平方等于两个连续正整数的和,则这个正奇数与这两个连续正整数是一组“勾股数”.其中结论正确的个数为( )
A.1个 B.2个 C.3个 D.4个
二、填空题(本大题共6小题,每小题2分,共12分)
11.直角三角形的两直角边均扩大到原来的3倍,则斜边扩大到原来的______倍.
12.已知一个直角三角形的两条直角边分别为、,那么这个直角三角形斜边上的高为______.
13.如图,∠C=90°,将直角△ABC沿着射线BC方向平移5cm,得△A'B'C',若BC=3cm,AC=4cm,则阴影部分的周长为______.
14.把一张矩形纸片(矩形ABCD)按如图方式折叠,使顶点B和点D重合,折痕为EF,若AB=3cm,BF=5cm,则重叠部分△DEF的面积是_____cm2.
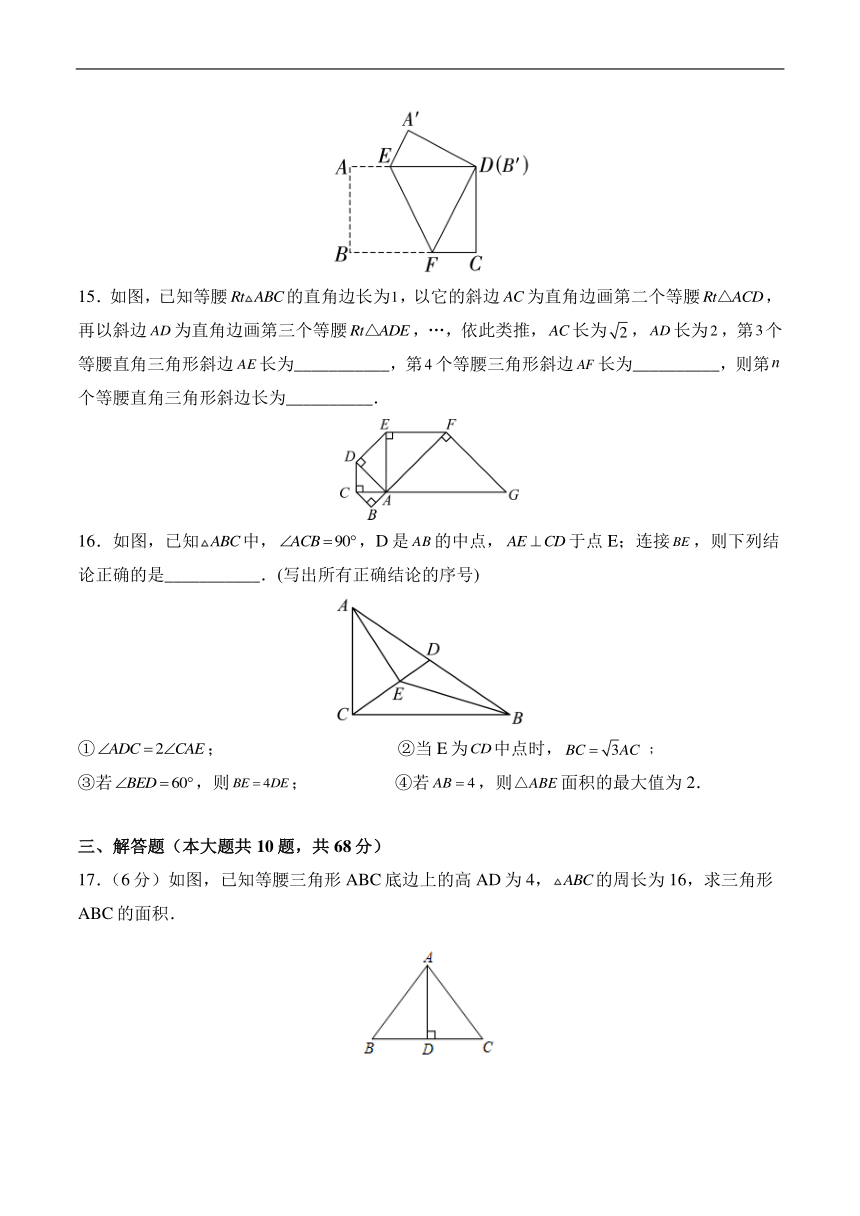
15.如图,已知等腰的直角边长为,以它的斜边为直角边画第二个等腰,再以斜边为直角边画第三个等腰,…,依此类推,长为,长为,第个等腰直角三角形斜边长为___________,第个等腰三角形斜边长为__________,则第个等腰直角三角形斜边长为__________.
16.如图,已知中,,D是的中点,于点E;连接,则下列结论正确的是___________.(写出所有正确结论的序号)
①; ②当E为中点时,﹔
③若,则; ④若,则面积的最大值为2.
三、解答题(本大题共10题,共68分)
17.(6分)如图,已知等腰三角形ABC底边上的高AD为4,的周长为16,求三角形ABC的面积.
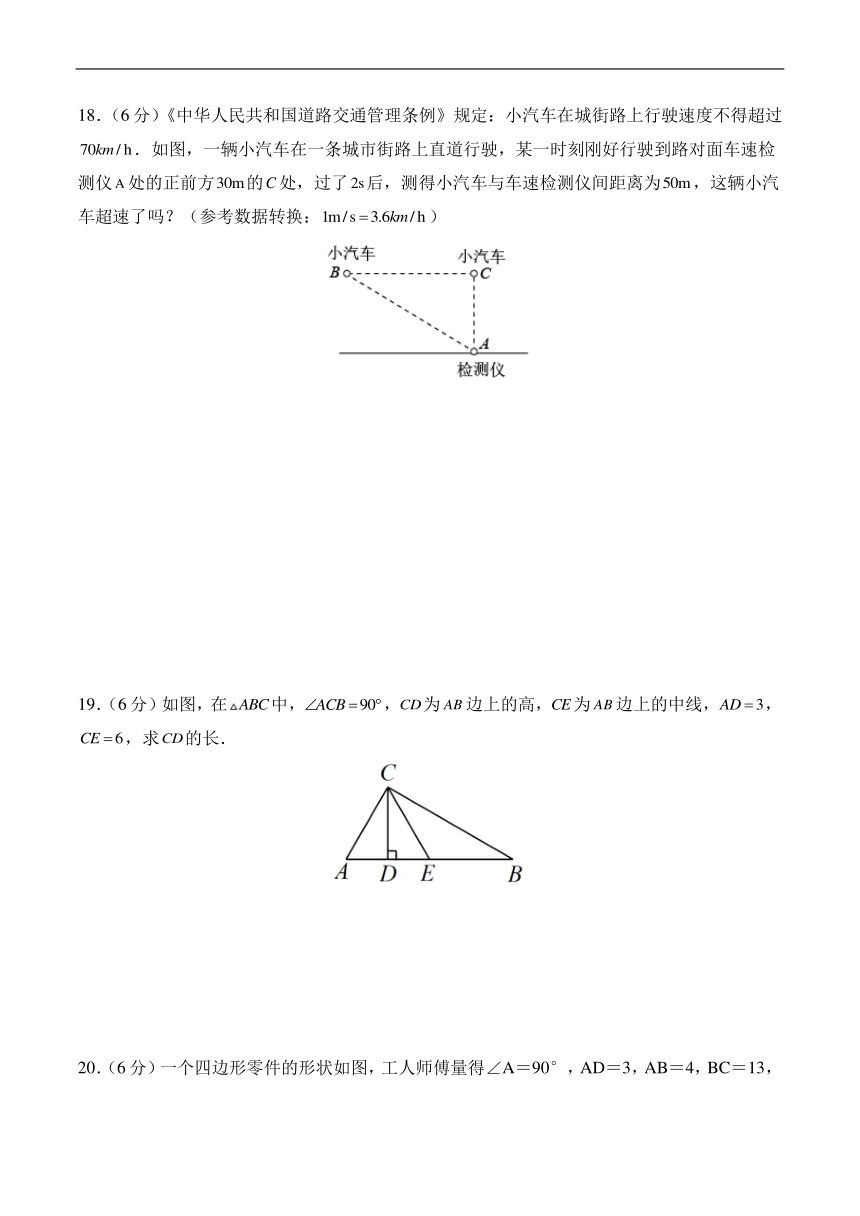
18.(6分)《中华人民共和国道路交通管理条例》规定:小汽车在城街路上行驶速度不得超过.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪处的正前方的处,过了后,测得小汽车与车速检测仪间距离为,这辆小汽车超速了吗?(参考数据转换:)
19.(6分)如图,在中,,为边上的高,为边上的中线,,,求的长.
20.(6分)一个四边形零件的形状如图,工人师傅量得∠A=90°,AD=3,AB=4,BC=13,DC=12,请你求出零件中的∠BDC的度数.
21.(6分)如图,在中,分别为边的中线,分别交于点D、E.
(1)若,求证:;
(2)若,,,求的长.
22.(6分)如图:和都等腰直角三角形,,,,的顶点A在的斜边DE上,
(1)求证:;
(2)试探究线段AC、AD、AE三条线段之间的数量关系,证明你的结论.
23.(6分)在等腰直角△ABC中,∠ACB=90°,P是线段BC上一动点(与点B,C不重合),连接AP,延长BC至点Q,使得CQ=CP,过点Q作.QH上AP于点H,交AB于点M.
(1)若∠PAC=α,则∠AMQ=______(用含有α的式子表示);
(2)用等式表示线段MB与PQ之间的数量关系,并证明.
24.(6分)如图,是等腰直角三角形,,,在线段上,是线段上的一点,连接,将线段以为旋转中心顺时针旋转得到线段,连接.
(1)如图1,猜想和的数量关系和位置关系,并说明理由;
(2)如图2,若,连接、,当运动到使得时,求的面积.
25.(10分)【情景呈现】画,并画的平分线.
(1)把三角尺的直角顶点落在的任意一点上,使三角尺的两条直角边分别与的两边,垂直,垂足为,,(如图1).则.(选填:“<”、“>”或“=”)(2)把三角尺绕点旋转(如图2),猜想,的大小关系,并说明理由.
【理解应用】
(3)在(2)的条件下,过点作直线,分别交,于点,,如图3猜想,,之间的关系为______.
【拓展延伸】
(4)如图4,画,并画的平分线,在上任取一点,作,的两边分别与,相交于,两点,与相等吗?请说明理由.
26.(10分)如图1,△ABC和△ADE均为等边三角形,点D在BC边上,连接CE.
(1)发现
①∠DCE的度数是 ;
②线段CA、CE、CD之间的数量关系是 .
(2)探究
如图2,△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,点D在BC边上,连接CE.请判断∠DCE的度数及线段CA、CE、CD之间的数量关系,并说明理由.
(3)拓展应用:
如图3,△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,点D在BC的延长线上,连接CE,若AB=AC=,CD=1,求线段DE的长.
答案
一、选择题
1.B
【解析】解:A.∵82+152≠162,
∴以a、b、c为边不能组成直角三角形,故本选项不符合题意;
B.∵92+122=152,
∴以a、b、c为边能组成直角三角形,故本选项符合题意;
C.∵92+402≠422,
∴以a、b、c为边不能组成直角三角形,故本选项不符合题意;
D.设a=2k,b=3k,c=4k,
∵(2k)2+(3k)2≠(4k)2,
∴以a、b、c为边不能组成直角三角形,故本选项不符合题意;
故选:B.
2.A
【解析】解:如图所示:
.
故选:A.
3.D
【解析】解:A、当是直角三角形且时,,故此选项不符合题意;
B、若,,是的三边,,则,故此选项不符合题意;
C、若,,是的三边,,则,故此选项不符合题意;
D、若,,是的三边,,则,故此选项符合题意.
故选:D.
4.A
【解析】当直吸管下端恰好位于罐底的圆周上时,如图所示,
则OA=3,AB=4,由勾股定理得:,
∴a=10-5=5;
当直吸管下端恰好位于罐底的中心时,则罐体内直吸管长为罐体的高即4,则a=10-4=6;
综上,直吸管露在罐外部分a的长度范围为.
故选:A.
5.D
【解析】解:由题意,得:AD=60km,
在Rt△ABD中,AB=100km,AD=60km,
∴BD=(km).
∴CD=BC-BD=125-80=45(km).
∴在Rt△ACD中,AC==75(km).
75÷25=3(h).
答:从C岛沿CA返回A港所需的时间为3h.
故选:D.
6.B
【解析】解:如图所示,
由题意可知,AC=EC,,
,
∴.
在和中,,
∴,
∴BC=DE.
∵,
即,.
在中,,
∴,,
即面积为的正方形的边长为.
故选:B.
7.C
【解析】解:设高为a对应的直角边的长为x,高为b对应的直角边的长为y,斜边为z,
∴,
∴,
∴,
∵,
∴,
∴,
故选C.
8.C
【解析】解:在中,
,
个直角三角形是全等的,
,
小正方形的边长,
阴影部分的面积,
故选:C.
9.A
【解析】解:由折叠得,,∠BAF=∠EAF,
在△BAF和△EAF中,
,
∴△BAF≌△EAF(SAS),
∴BF=EF,
∴AF⊥BE,
又∵AF=4,AB=5,
∴,
在△ADE中,EF⊥AD,DG=EG,设DE边上的高线长为h,
∴,
即,
∵,,
∴,
∴,
∴,
∴,
在Rt△BDF中,,,
∴,
故选:A.
10.C
【解析】解:①∵
∴20是“整弦数”,符合题意;
②如5,2是“整弦数”,
∵不是“整弦数”,
∴两个“整弦数”之和不一定是“整弦数”,不符合题意;
③若,则,,c2为“整弦数”,则c为正整数”,不符合题意;
④∵m=a12+b12,n=a22+b22,≠,且m,n,a1,a2,b1,b2均为正整数,
∴m与n之积为“整弦数”,符合题意;
⑤设一个正奇数(除1外)为2n+1(n为正整数),
∵(2n+1)2=4n2+4n+1且等于两个连续正整数的和,
∴较小的正整数为2n2+2n,较小的正整数为2n2+2n+1,
∵(2n+1)2+(2n2+2n)2=(2n2+2n)2+4n2+4n+1=(2n2+2n)2+2(2n2+2n)+1=(2n2+2n+1)2,
∴这个正奇数与这两个连续正整数是一组“勾股数”,符合题意.
故选:C.
二、填空题
11.3
【解析】解:设直角三角形直角边为a、b,斜边为c,则a2+b2=c2;
扩大3倍后,直角三角形直角边为3a、3b,则根据勾股定理知斜边为
=3c.即直角三角形两直角边都扩大到原来的3倍,
则斜边扩大到原来的3倍.
故答案为3.
12.
【解析】解:设这个直角三角形斜边上的高为,
由勾股定理得,直角三角形斜边长,
由三角形的面积公式得,,
解得,,
故答案为: .
13.
【解析】解:在Rt△ACB中,AB=
∵AA′=BB′=5cm,
∴CB′=BB′-BC=5-3=2(cm),
∴阴影部分的周长=AC+CB′+A′B′+AA′=4+2+5+5=16(cm).
故答案为:16cm.
14.
【解析】解:∵AB=3cm,BF=5cm,
由折叠的性质可得,, ,
在中,由勾股定理得:
∴,,
设DE=x,则=(9 x) cm,
在中,由勾股定理得:
,
∴(9 x)2+9=x 2,
解得:x=5,
∴DE=5(cm),
∴△DEF的面积是:×5×3=(cm2).
15.
【解析】解:在直角三角形中由勾股定理可以得出:
第一个等腰三角形斜边长为:,
第二个等腰三角形斜边长为:,
第三个等腰三角形斜边长为:,
第四个等腰三角形斜边长为:,
……依此类推,
第个等腰三角形斜边长为:.
故答案为:;;.
16.①②③④
【解析】解:△ABC中,∠ACB=90°,D是AB的中点,
∴CD=BD=AD,
∴∠DCB=∠DBC,
∴∠ADC=2∠DCB,
∵AE⊥CD于点E,
∴∠ACE+∠CAE=90°,
∵∠ACE+∠DCB=90°,
∴∠CAE=∠DCB,
∴∠ADC=2∠CAE,故①正确;
当E为CD中点时,∵AE⊥CD,
∴AC=AD,
∴△ACD是等边三角形,
∴∠BAC=60°,
∴BC=AC,故②正确;
作BM⊥CD,交CD的延长线于点M,则AE∥BM,
∴∠DAE=∠DBM,
∵∠ADE=∠BDM,AD=BD,
∴△ADE≌△BDM(AAS),
∴DE=DM,
若∠BED=60°,则BE=2EM=4DE,故③正确;
∵△ADE≌△BDM,
∴AE=BM,DE=DM,
∴S△ABE=S△BEM= BM EM= AE 2DE=AE DE,
若AB=4,则AD=2,
在Rt△ADE中,AD2=AE2+DE2,
即的最大值值为1,
∴△ABE面积的最大值为2,故④正确;
故答案为:①②③④.
三、解答题
17.解:∵AD是底边BC上的高,
∴,
设BD=x,
∵△ABC的周长为16,
∴AB+BD=8,AB=8-x,
在Rt△ABD中,∠ADB=90°,
∴,
解得:,
∴BC=2BD=6,
∴.
18.解:根据题意,,,
∴在中,
,
∴小汽车的速度为,
∵,
∴这辆小汽车超速行驶.
19.解:∵,为边上的中线
∴,
∴
∵
∴
∴在中
.
20.解:∵∠A=90°,AD=3,AB=4,
∴BD==5.
∵BC=13,DC=12,,
∴,
∴△BDC是直角三角形,∠BDC=90°.
21.(1)证明:∵AD、BE分别为边BC、AC的中线,CD=4,CE=3.
∴AC=6,BC=8.
∵.
∴.
∴△ABC是直角三角形.
∴.
(2)解:∵∠C=90°,AD=6,BE=8,
∴,.
∵AD、BE分别为边BC、AC的中线.
∴,.
∴,.
∴.
∴.
∴.
22.(1)∵,
∴
∴
∴△ACE≌△BCD(SAS)
∴
(2)线段AC,AD,AE三条线段的数量关系是
∵△ECD是等腰直角三角形,
∴∠E=∠EDC=45°
由(1)知:
∴
即,
又为等腰直角三角形,且,
∴,
即.
23.(1)∵∠PAC=α,△ACB是等腰直角三角形,
∴∠BAC=∠B=45°,∠PAB=45°-α,
∵QH⊥AP,
∴∠AHM=90°,
∴∠AMQ=180°-∠AHM-∠PAB=45°+α;
故答案为:∠AMQ=45°+α
(2)PQ=MB;理由如下:
连接AQ,作ME⊥QB,如图所示:
∵AC⊥QP,CQ=CP,
∴∠QAC=∠PAC=α,
∴∠QAM=45°+α=∠AMQ,
∴AP=AQ=QM,
在△APC和△QME中,
,
∴△APC≌△QME(AAS),
∴PC=ME,
∵△MEB是等腰直角三角形,
∴PQ=MB .即.
24.(1),,
证明:如图1,延长交于点,
∵将线段以为旋转中心顺时针旋转得到线段,
∴,,
∵,
∴,
∴,
∵,
∴,
∴,,
∵,
∴,
∴,即.
(2)如图2,作于点,于点,
∵在等腰直角中,,,
∴.
∵,
∴,
∵,
∴,
∵,
∴,,
∴,,
∵,,
∴,
在中,,
∴,即,
∴,,
∵,,
∴是等边三角形,
∴,
∵,即,
∴,
∴,,
∴
25.(1)解:∵OC平分∠AOB,
∴∠AOC=∠BOC,
∵PE⊥OA,
∴∠OEP=90°,
∵∠AOB=90°,∠EPF=90°
∴∠OFP=360°-∠AOB-∠PEO-∠EPF=90°,
∴∠OEP=∠OFP
又∵∠AOC=∠BOC,OP=OP
∴△OEP≌△OFP(AAS),
∴PE=PF,
故答案为:=;
(2)解:PE=PF,理由如下:如图2,过点P作PM⊥OA,PN⊥OB,垂足是M,N,
∵PM⊥OA,PN⊥OB,,
∴∠AOB=∠PME=∠PNF=90°,
∴∠MPN=90°,
与(1)同理可证PM=PN,
∵∠EPF=90°,
∴∠MPE=∠FPN,
在△PEM和△PFN中,
,
∴△PEM≌△PFN(ASA),
∴PE=PF;
(3)解:GE2+FH2=EF2,理由如下:
∵OC平分∠AOB,
∴∠AOC=∠BOC=45°,
∵GH⊥OC,
∴∠OGH=∠OHG=45°,
∴OP=PG=PH,
∵∠GPO=90°,∠EPF=90°,
∴∠GPE=∠OPF,
在△GPE和△OPF中,
,
∴△GPE≌△OPF(ASA),
∴GE=OF,
同理可证明△EPO≌△FPH,
∴∴FH=OE,
在Rt△EOF中,OF2+OE2=EF2,
∴GE2+FH2=EF2,
故答案为:GE2+FH2=EF2;
(4)解:PE=PF;理由:作PG⊥OA于G,PH⊥OB于H.
在△OPG和△OPH中,
,
∴△OPG≌△OPH,
∴PG=PH,
∵∠AOB=60°,∠PGO=∠PHO=90°,
∴∠GPH=120°,
∵∠EPF=120°,
∴∠GPH=∠EPF,
∴∠GPE=∠FPH,
在△PGE和△PHF中,
∴△PGE≌△PHF,
∴PE=PF.
26.(1)发现解:①∵△ABC和△ADE均为等边三角形,
∴∠BAC=∠DAE=60°,AB=AC,AD=AE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,即∠BAD=∠CAE,
在△BAD和△CAE中,,
∴△BAD≌△CAE(SAS),
∴∠ACE=∠B,
∵∠ABC=∠ACB=60°,
∴∠ACE=60°,
∴∠DCE=∠ACE+∠ACB=60°+60°=120°;
故答案为:120°,
②∵△BAD≌△CAE,
∴BD=CE,
∴BC=BD+CD=EC+CD,
∴CA=BC=CE+CD;
故答案为:CA=CE+CD.
(2)探究∠DCE=90°;CA=CD+CE.理由:
∵△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,
∴AB=AC,AD=AE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,即∠BAD=∠CAE.
∴△BAD≌△CAE(SAS).
∴BD=CE,∠B=∠ACE.
∵∠B=∠ACB=(180°-∠BAC)=45°,
∴∠ACE=45°,
∴∠DCE=∠ACB+∠ACE=90°.
∵在等腰直角三角形ABC中,CB=CA,且CB=CD+DB=CD+CE,
∴CA=CD+CE.
(3)应用∵△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,点D在BC的延长线上,AB=AC=,CD=1,
∴,AD=AE,
∴BD=BC+CD=3,
∵∠BAC+∠CAD=∠DAE+∠CAD,
∴∠BAD=∠CAE,
∴△ABD≌△ACE(SAS),
∴CE=BD=3,∠ABD=∠ACE,
∵∠B=∠ACB=(180°-∠BAC)=45°,
∴∠ACE=45°,
∴∠DCE=∠ACB+∠ACE=90°,
∴.
一、选择题(本大题共10小题,每小题2分,共20分)
1.下列三条线段能组成直角三角形的是( )
A. B.
C. D.
2.如图,在边长为1个单位长度的小正方形组成的网格中,点A,B都是格点,则线段AB的长度为( )
A.5 B.6 C.7 D.9
3.下列说法正确的是( )
A.若,,是的三边,则
B.若,,是的三边,则
C.若,,是的三边,,则
D.若,,是的三边,,则
4.如图是一个圆柱形饮料罐,底面半径是3,高是4,上底面中心有一个小圆孔,则一条长10cm的直吸管露在罐外部分的长度(罐壁的厚度和小圆孔的大小忽略不计)范围是( )
A. B. C. D.
5.一艘轮船从A港向南偏西方向航行到达B岛,再从B岛沿方向航行到达C岛,A港到航线的最短距离是.若轮船速度为,轮船从C岛沿返回A港所需的时间是( )
A. B. C. D.
6.如图,直线上有三个正方形,面积分别为S1,S2,S3,己知,则面积为的正方形的边长为( ).
A. B.2 C.3 D.12
7.设直角三角形的两条直角边长及斜边上的高分别为a,b及h,则a,b,h的数量关系是( )
A. B. C. D.
8.如图,“赵爽弦图”是吴国的赵爽创制的.以直角三角形的斜边为边长得到一个正方形,该正方形由4个全等的直角三角形再加上中间的小正方形组成,在一次游园活动中,数学小组制作了一面“赵爽弦图锣”,其中∠AEB=90°,AB=13cm,BE=5cm,则阴影部分的面积是( )
A.169cm2 B.25cm2 C.49cm2 D.64cm2
9.如图,三角形纸片ABC中,点D是BC边上一点,连接AD,把△ABD沿着直线AD翻折,得到△AED,DE交AC于点G,连接BE交AD于点F.若DG=EG,AF=4,AB=5,△AEG的面积为,则的值为( )
A.13 B.12 C.11 D.10
10.中国古代称直角三角形为勾股形,如果勾股形的三边长为三个正整数,则称三边长叫“勾股数”;如果勾股形的两直角边长为正整数,那么称斜边长的平方叫“整弦数”对于以下结论:①20是“整弦数”;②两个“整弦数”之和一定是“整弦数”;③若c2为“整弦数”,则c不可能为正整数;④若m=a12+b12,n=a22+b22,≠,且m,n,a1,a2,b1,b2均为正整数,则m与n之积为“整弦数”;⑤若一个正奇数(除1外)的平方等于两个连续正整数的和,则这个正奇数与这两个连续正整数是一组“勾股数”.其中结论正确的个数为( )
A.1个 B.2个 C.3个 D.4个
二、填空题(本大题共6小题,每小题2分,共12分)
11.直角三角形的两直角边均扩大到原来的3倍,则斜边扩大到原来的______倍.
12.已知一个直角三角形的两条直角边分别为、,那么这个直角三角形斜边上的高为______.
13.如图,∠C=90°,将直角△ABC沿着射线BC方向平移5cm,得△A'B'C',若BC=3cm,AC=4cm,则阴影部分的周长为______.
14.把一张矩形纸片(矩形ABCD)按如图方式折叠,使顶点B和点D重合,折痕为EF,若AB=3cm,BF=5cm,则重叠部分△DEF的面积是_____cm2.
15.如图,已知等腰的直角边长为,以它的斜边为直角边画第二个等腰,再以斜边为直角边画第三个等腰,…,依此类推,长为,长为,第个等腰直角三角形斜边长为___________,第个等腰三角形斜边长为__________,则第个等腰直角三角形斜边长为__________.
16.如图,已知中,,D是的中点,于点E;连接,则下列结论正确的是___________.(写出所有正确结论的序号)
①; ②当E为中点时,﹔
③若,则; ④若,则面积的最大值为2.
三、解答题(本大题共10题,共68分)
17.(6分)如图,已知等腰三角形ABC底边上的高AD为4,的周长为16,求三角形ABC的面积.
18.(6分)《中华人民共和国道路交通管理条例》规定:小汽车在城街路上行驶速度不得超过.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪处的正前方的处,过了后,测得小汽车与车速检测仪间距离为,这辆小汽车超速了吗?(参考数据转换:)
19.(6分)如图,在中,,为边上的高,为边上的中线,,,求的长.
20.(6分)一个四边形零件的形状如图,工人师傅量得∠A=90°,AD=3,AB=4,BC=13,DC=12,请你求出零件中的∠BDC的度数.
21.(6分)如图,在中,分别为边的中线,分别交于点D、E.
(1)若,求证:;
(2)若,,,求的长.
22.(6分)如图:和都等腰直角三角形,,,,的顶点A在的斜边DE上,
(1)求证:;
(2)试探究线段AC、AD、AE三条线段之间的数量关系,证明你的结论.
23.(6分)在等腰直角△ABC中,∠ACB=90°,P是线段BC上一动点(与点B,C不重合),连接AP,延长BC至点Q,使得CQ=CP,过点Q作.QH上AP于点H,交AB于点M.
(1)若∠PAC=α,则∠AMQ=______(用含有α的式子表示);
(2)用等式表示线段MB与PQ之间的数量关系,并证明.
24.(6分)如图,是等腰直角三角形,,,在线段上,是线段上的一点,连接,将线段以为旋转中心顺时针旋转得到线段,连接.
(1)如图1,猜想和的数量关系和位置关系,并说明理由;
(2)如图2,若,连接、,当运动到使得时,求的面积.
25.(10分)【情景呈现】画,并画的平分线.
(1)把三角尺的直角顶点落在的任意一点上,使三角尺的两条直角边分别与的两边,垂直,垂足为,,(如图1).则.(选填:“<”、“>”或“=”)(2)把三角尺绕点旋转(如图2),猜想,的大小关系,并说明理由.
【理解应用】
(3)在(2)的条件下,过点作直线,分别交,于点,,如图3猜想,,之间的关系为______.
【拓展延伸】
(4)如图4,画,并画的平分线,在上任取一点,作,的两边分别与,相交于,两点,与相等吗?请说明理由.
26.(10分)如图1,△ABC和△ADE均为等边三角形,点D在BC边上,连接CE.
(1)发现
①∠DCE的度数是 ;
②线段CA、CE、CD之间的数量关系是 .
(2)探究
如图2,△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,点D在BC边上,连接CE.请判断∠DCE的度数及线段CA、CE、CD之间的数量关系,并说明理由.
(3)拓展应用:
如图3,△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,点D在BC的延长线上,连接CE,若AB=AC=,CD=1,求线段DE的长.
答案
一、选择题
1.B
【解析】解:A.∵82+152≠162,
∴以a、b、c为边不能组成直角三角形,故本选项不符合题意;
B.∵92+122=152,
∴以a、b、c为边能组成直角三角形,故本选项符合题意;
C.∵92+402≠422,
∴以a、b、c为边不能组成直角三角形,故本选项不符合题意;
D.设a=2k,b=3k,c=4k,
∵(2k)2+(3k)2≠(4k)2,
∴以a、b、c为边不能组成直角三角形,故本选项不符合题意;
故选:B.
2.A
【解析】解:如图所示:
.
故选:A.
3.D
【解析】解:A、当是直角三角形且时,,故此选项不符合题意;
B、若,,是的三边,,则,故此选项不符合题意;
C、若,,是的三边,,则,故此选项不符合题意;
D、若,,是的三边,,则,故此选项符合题意.
故选:D.
4.A
【解析】当直吸管下端恰好位于罐底的圆周上时,如图所示,
则OA=3,AB=4,由勾股定理得:,
∴a=10-5=5;
当直吸管下端恰好位于罐底的中心时,则罐体内直吸管长为罐体的高即4,则a=10-4=6;
综上,直吸管露在罐外部分a的长度范围为.
故选:A.
5.D
【解析】解:由题意,得:AD=60km,
在Rt△ABD中,AB=100km,AD=60km,
∴BD=(km).
∴CD=BC-BD=125-80=45(km).
∴在Rt△ACD中,AC==75(km).
75÷25=3(h).
答:从C岛沿CA返回A港所需的时间为3h.
故选:D.
6.B
【解析】解:如图所示,
由题意可知,AC=EC,,
,
∴.
在和中,,
∴,
∴BC=DE.
∵,
即,.
在中,,
∴,,
即面积为的正方形的边长为.
故选:B.
7.C
【解析】解:设高为a对应的直角边的长为x,高为b对应的直角边的长为y,斜边为z,
∴,
∴,
∴,
∵,
∴,
∴,
故选C.
8.C
【解析】解:在中,
,
个直角三角形是全等的,
,
小正方形的边长,
阴影部分的面积,
故选:C.
9.A
【解析】解:由折叠得,,∠BAF=∠EAF,
在△BAF和△EAF中,
,
∴△BAF≌△EAF(SAS),
∴BF=EF,
∴AF⊥BE,
又∵AF=4,AB=5,
∴,
在△ADE中,EF⊥AD,DG=EG,设DE边上的高线长为h,
∴,
即,
∵,,
∴,
∴,
∴,
∴,
在Rt△BDF中,,,
∴,
故选:A.
10.C
【解析】解:①∵
∴20是“整弦数”,符合题意;
②如5,2是“整弦数”,
∵不是“整弦数”,
∴两个“整弦数”之和不一定是“整弦数”,不符合题意;
③若,则,,c2为“整弦数”,则c为正整数”,不符合题意;
④∵m=a12+b12,n=a22+b22,≠,且m,n,a1,a2,b1,b2均为正整数,
∴m与n之积为“整弦数”,符合题意;
⑤设一个正奇数(除1外)为2n+1(n为正整数),
∵(2n+1)2=4n2+4n+1且等于两个连续正整数的和,
∴较小的正整数为2n2+2n,较小的正整数为2n2+2n+1,
∵(2n+1)2+(2n2+2n)2=(2n2+2n)2+4n2+4n+1=(2n2+2n)2+2(2n2+2n)+1=(2n2+2n+1)2,
∴这个正奇数与这两个连续正整数是一组“勾股数”,符合题意.
故选:C.
二、填空题
11.3
【解析】解:设直角三角形直角边为a、b,斜边为c,则a2+b2=c2;
扩大3倍后,直角三角形直角边为3a、3b,则根据勾股定理知斜边为
=3c.即直角三角形两直角边都扩大到原来的3倍,
则斜边扩大到原来的3倍.
故答案为3.
12.
【解析】解:设这个直角三角形斜边上的高为,
由勾股定理得,直角三角形斜边长,
由三角形的面积公式得,,
解得,,
故答案为: .
13.
【解析】解:在Rt△ACB中,AB=
∵AA′=BB′=5cm,
∴CB′=BB′-BC=5-3=2(cm),
∴阴影部分的周长=AC+CB′+A′B′+AA′=4+2+5+5=16(cm).
故答案为:16cm.
14.
【解析】解:∵AB=3cm,BF=5cm,
由折叠的性质可得,, ,
在中,由勾股定理得:
∴,,
设DE=x,则=(9 x) cm,
在中,由勾股定理得:
,
∴(9 x)2+9=x 2,
解得:x=5,
∴DE=5(cm),
∴△DEF的面积是:×5×3=(cm2).
15.
【解析】解:在直角三角形中由勾股定理可以得出:
第一个等腰三角形斜边长为:,
第二个等腰三角形斜边长为:,
第三个等腰三角形斜边长为:,
第四个等腰三角形斜边长为:,
……依此类推,
第个等腰三角形斜边长为:.
故答案为:;;.
16.①②③④
【解析】解:△ABC中,∠ACB=90°,D是AB的中点,
∴CD=BD=AD,
∴∠DCB=∠DBC,
∴∠ADC=2∠DCB,
∵AE⊥CD于点E,
∴∠ACE+∠CAE=90°,
∵∠ACE+∠DCB=90°,
∴∠CAE=∠DCB,
∴∠ADC=2∠CAE,故①正确;
当E为CD中点时,∵AE⊥CD,
∴AC=AD,
∴△ACD是等边三角形,
∴∠BAC=60°,
∴BC=AC,故②正确;
作BM⊥CD,交CD的延长线于点M,则AE∥BM,
∴∠DAE=∠DBM,
∵∠ADE=∠BDM,AD=BD,
∴△ADE≌△BDM(AAS),
∴DE=DM,
若∠BED=60°,则BE=2EM=4DE,故③正确;
∵△ADE≌△BDM,
∴AE=BM,DE=DM,
∴S△ABE=S△BEM= BM EM= AE 2DE=AE DE,
若AB=4,则AD=2,
在Rt△ADE中,AD2=AE2+DE2,
即的最大值值为1,
∴△ABE面积的最大值为2,故④正确;
故答案为:①②③④.
三、解答题
17.解:∵AD是底边BC上的高,
∴,
设BD=x,
∵△ABC的周长为16,
∴AB+BD=8,AB=8-x,
在Rt△ABD中,∠ADB=90°,
∴,
解得:,
∴BC=2BD=6,
∴.
18.解:根据题意,,,
∴在中,
,
∴小汽车的速度为,
∵,
∴这辆小汽车超速行驶.
19.解:∵,为边上的中线
∴,
∴
∵
∴
∴在中
.
20.解:∵∠A=90°,AD=3,AB=4,
∴BD==5.
∵BC=13,DC=12,,
∴,
∴△BDC是直角三角形,∠BDC=90°.
21.(1)证明:∵AD、BE分别为边BC、AC的中线,CD=4,CE=3.
∴AC=6,BC=8.
∵.
∴.
∴△ABC是直角三角形.
∴.
(2)解:∵∠C=90°,AD=6,BE=8,
∴,.
∵AD、BE分别为边BC、AC的中线.
∴,.
∴,.
∴.
∴.
∴.
22.(1)∵,
∴
∴
∴△ACE≌△BCD(SAS)
∴
(2)线段AC,AD,AE三条线段的数量关系是
∵△ECD是等腰直角三角形,
∴∠E=∠EDC=45°
由(1)知:
∴
即,
又为等腰直角三角形,且,
∴,
即.
23.(1)∵∠PAC=α,△ACB是等腰直角三角形,
∴∠BAC=∠B=45°,∠PAB=45°-α,
∵QH⊥AP,
∴∠AHM=90°,
∴∠AMQ=180°-∠AHM-∠PAB=45°+α;
故答案为:∠AMQ=45°+α
(2)PQ=MB;理由如下:
连接AQ,作ME⊥QB,如图所示:
∵AC⊥QP,CQ=CP,
∴∠QAC=∠PAC=α,
∴∠QAM=45°+α=∠AMQ,
∴AP=AQ=QM,
在△APC和△QME中,
,
∴△APC≌△QME(AAS),
∴PC=ME,
∵△MEB是等腰直角三角形,
∴PQ=MB .即.
24.(1),,
证明:如图1,延长交于点,
∵将线段以为旋转中心顺时针旋转得到线段,
∴,,
∵,
∴,
∴,
∵,
∴,
∴,,
∵,
∴,
∴,即.
(2)如图2,作于点,于点,
∵在等腰直角中,,,
∴.
∵,
∴,
∵,
∴,
∵,
∴,,
∴,,
∵,,
∴,
在中,,
∴,即,
∴,,
∵,,
∴是等边三角形,
∴,
∵,即,
∴,
∴,,
∴
25.(1)解:∵OC平分∠AOB,
∴∠AOC=∠BOC,
∵PE⊥OA,
∴∠OEP=90°,
∵∠AOB=90°,∠EPF=90°
∴∠OFP=360°-∠AOB-∠PEO-∠EPF=90°,
∴∠OEP=∠OFP
又∵∠AOC=∠BOC,OP=OP
∴△OEP≌△OFP(AAS),
∴PE=PF,
故答案为:=;
(2)解:PE=PF,理由如下:如图2,过点P作PM⊥OA,PN⊥OB,垂足是M,N,
∵PM⊥OA,PN⊥OB,,
∴∠AOB=∠PME=∠PNF=90°,
∴∠MPN=90°,
与(1)同理可证PM=PN,
∵∠EPF=90°,
∴∠MPE=∠FPN,
在△PEM和△PFN中,
,
∴△PEM≌△PFN(ASA),
∴PE=PF;
(3)解:GE2+FH2=EF2,理由如下:
∵OC平分∠AOB,
∴∠AOC=∠BOC=45°,
∵GH⊥OC,
∴∠OGH=∠OHG=45°,
∴OP=PG=PH,
∵∠GPO=90°,∠EPF=90°,
∴∠GPE=∠OPF,
在△GPE和△OPF中,
,
∴△GPE≌△OPF(ASA),
∴GE=OF,
同理可证明△EPO≌△FPH,
∴∴FH=OE,
在Rt△EOF中,OF2+OE2=EF2,
∴GE2+FH2=EF2,
故答案为:GE2+FH2=EF2;
(4)解:PE=PF;理由:作PG⊥OA于G,PH⊥OB于H.
在△OPG和△OPH中,
,
∴△OPG≌△OPH,
∴PG=PH,
∵∠AOB=60°,∠PGO=∠PHO=90°,
∴∠GPH=120°,
∵∠EPF=120°,
∴∠GPH=∠EPF,
∴∠GPE=∠FPH,
在△PGE和△PHF中,
∴△PGE≌△PHF,
∴PE=PF.
26.(1)发现解:①∵△ABC和△ADE均为等边三角形,
∴∠BAC=∠DAE=60°,AB=AC,AD=AE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,即∠BAD=∠CAE,
在△BAD和△CAE中,,
∴△BAD≌△CAE(SAS),
∴∠ACE=∠B,
∵∠ABC=∠ACB=60°,
∴∠ACE=60°,
∴∠DCE=∠ACE+∠ACB=60°+60°=120°;
故答案为:120°,
②∵△BAD≌△CAE,
∴BD=CE,
∴BC=BD+CD=EC+CD,
∴CA=BC=CE+CD;
故答案为:CA=CE+CD.
(2)探究∠DCE=90°;CA=CD+CE.理由:
∵△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,
∴AB=AC,AD=AE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,即∠BAD=∠CAE.
∴△BAD≌△CAE(SAS).
∴BD=CE,∠B=∠ACE.
∵∠B=∠ACB=(180°-∠BAC)=45°,
∴∠ACE=45°,
∴∠DCE=∠ACB+∠ACE=90°.
∵在等腰直角三角形ABC中,CB=CA,且CB=CD+DB=CD+CE,
∴CA=CD+CE.
(3)应用∵△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,点D在BC的延长线上,AB=AC=,CD=1,
∴,AD=AE,
∴BD=BC+CD=3,
∵∠BAC+∠CAD=∠DAE+∠CAD,
∴∠BAD=∠CAE,
∴△ABD≌△ACE(SAS),
∴CE=BD=3,∠ABD=∠ACE,
∵∠B=∠ACB=(180°-∠BAC)=45°,
∴∠ACE=45°,
∴∠DCE=∠ACB+∠ACE=90°,
∴.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
