21.3 实际问题与一元二次方程 同步练习(含答案)人教版数学九年级上册
文档属性
| 名称 | 21.3 实际问题与一元二次方程 同步练习(含答案)人教版数学九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 474.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-08 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
21.3实际问题与一元二次方程
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.为执行国家药品降价政策,给人民群众带来实惠,某药品经过两次降价,每盒零售价由56元降为31.5元,设平均每次降价的百分率是x,则根据题意,下列方程正确的是( )
A.56(1﹣2x)=31.5 B.56(1﹣x)2=31.5
C.31.5(1+x)2=56 D.31.5(1+2x)=56
2.从正方形铁片,截去宽的一条长方形,余下的矩形的面积是,则原来的正方形铁片的面积是( )
A. B. C. D.
3.某经济开发区今年一月份工业产值达到80亿元,第一季度总产值为275亿元,问二、三月平均每月的增长率是多少?设平均每月的增长率为x,根据题意所列方程是( )
A.80(1+x)2=275 B.80+80(1+x)+80(1+x)2=275
C.80(1+x)3=275 D.80(1+x)+80(1+x)2=275
4.某公司员工2018年的人均年收入为18万元,2020年的人均年收入为23万元,设年平均增长率为x,根据题意,可列出方程为( )
A. B.
C. D.
5.《周髀算经》中有一种几何方法可以用来解形如x(x+5)=24的方程的正数解,方法为:如图,将四个长为x+5,宽为x的长方形纸片(面积均为24)拼成一个大正方形,于是大正方形的面积为:24×4+25=121,边长为11,故得x(x+5)=24的正数解为x= ,小明按此方法解关于x的方程x2+mx﹣n=0时,构造出同样的图形.已知大正方形的面积为10,小正方形的面积为4,则( )
A.m=2,n=3 B.m= ,n=2 C.m= ,n=2 D.m=2,n=
6.从一块正方形铁皮上截去2cm宽的一个长方形,余下的面积是48cm2,则原来正方形的面积为( )
A.56cm2 B.64cm2 C.81cm2 D.100cm2
7.按照党中央、国务院决策部署,为了活跃市场主体、助推各地区经济发展,各省市地区抓紧推动稳经济一揽子政策落实落地.江夏区制定了“黄金十条”,坚定企业疫后发展信心,促进企业稳步高效增长.2022年我区某企业4月份的利润是100万元,第二季度的总利润达到500万元,设利润平均月增长率为x,则依题意列方程为( )
A. B.
C. D.
8.电影《流浪地球2》于2023年1月22日在中国上映,第一天票房约4亿,以后每天票房按相同的增长率增长,前三天票房累计约10亿,若把增长率记作x,则方程可以列为( )
A. B.
C. D.
9.《九章算术》是我国古代内容极为丰富的数学名著,其中“勾股”章有一题,大意是:已知矩形门的高比宽多6尺,门的对角线长10尺,那么门的高和宽各是多少?如果设门的宽为x尺.根据题意,所列方程为( )
A. B. C. D.
10.有一块长30m、宽20m的矩形田地,准备修筑同样宽的三条直路(如图),把田地分成六块,种植不同品种的蔬菜,并且种植蔬菜面积为基地面积的.设道路的宽度为m,下列方程:①;②;③.其中正确的是( )
A.①② B.①③ C.②③ D.③
11.“读书可以让人保持思想活力,让人得到智慧启发,让人滋养浩然之气”某校为响应我市全民阅读活动,利用节假日面向社会开放学校图书馆.据统计,第一个月进馆324人次,进馆人次逐月增加,第三个月进馆1600人次.若进馆人次的月平均增长率为x,由题意可列方程( )
A. B.
C. D.
12.某口罩经销商批发了一批口罩,进货单价为每盒50元,若按每盒60元出售,则每周可销售80盒.现准备提价销售,经市场调研发现:每盒每提价1元,每周销量就会减少2盒,为保护消费者利益,物价部门规定,销售时利润率不能超过50%,设该口罩售价为每盒元,现在预算销售这种口罩每周要获得1200元利润,则每盒口罩的售价应定为( )
A.70元 B.80元 C.70元或80元 D.75元
二、填空题
13.如图,将面积为25的正方形的边的长度增加,变为面积为22的矩形.若正方形和矩形的周长相等,则的值是 .
14.随着居民经济收入的不断提高以及汽车业的快速发展,家用汽车已越来越多地进入普通家庭.抽样调查显示,截止至2020年底某市汽车拥有量为21.6万辆,已知2018年底该市汽车拥有量为15万辆,设2018年底至2020年底该市汽车拥有量的年平均增长率为,根据题意列方程得 .
15.有一个人患了流感,经过两轮传染后得知共传染400人,如果每轮传染率都相同,那么每轮传染中平均一个人传染了 个人
16.某市某楼盘准备以每平方米7200元的均价对外销售,由于国务院有关房地产的新政策出台后,购房者持币观望,为了加快资金周转,房地产开发商对价格经过两次下调后,决定以每平方米5832元的均价开盘销售.则平均每次下调的百分率为 .
17.同学聚会,每两人都握手一次,共握手45次,设x人参加聚会,可列方程为 .
三、解答题
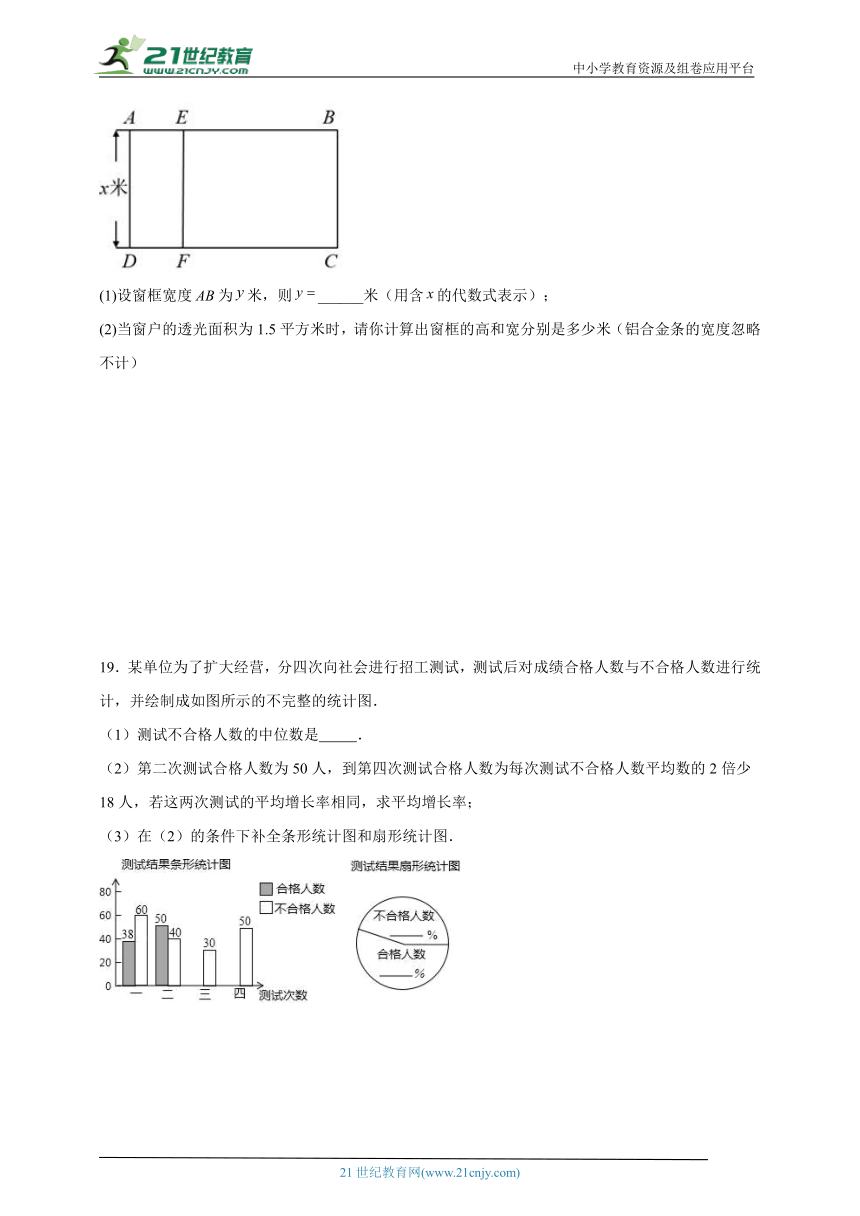
18.用长为6米的铅合金条制成如图所示的矩形窗框,其中////,设窗框的高度为米.
(1)设窗框宽度为米,则______米(用含的代数式表示);
(2)当窗户的透光面积为1.5平方米时,请你计算出窗框的高和宽分别是多少米(铝合金条的宽度忽略不计)
19.某单位为了扩大经营,分四次向社会进行招工测试,测试后对成绩合格人数与不合格人数进行统计,并绘制成如图所示的不完整的统计图.
(1)测试不合格人数的中位数是 .
(2)第二次测试合格人数为50人,到第四次测试合格人数为每次测试不合格人数平均数的2倍少18人,若这两次测试的平均增长率相同,求平均增长率;
(3)在(2)的条件下补全条形统计图和扇形统计图.
20.商场销售某种商品,每件进价100元,若每件售价150元,平均每天售出60件.经调查发现:当商品售价每降低1元时,平均每天可多售出3件.
(1)当商品售价降低5元时,每天销售量可达到______件,每天盈利______元.
(2)为了减少库存,每件商品降价多少元时,商场通过销售这种商品每天盈利3600元?
21.近年我市积极推进“智慧校园”建设,加大对学校教育信息化的建设的投入,去年投入2000万元,之后逐步增加投入,按计划明年投入达到2880万元,求投入经费的年平均增长率.
22.某人将1000元人民币按一年期存入银行,到期后将本金和利息再按一年期存入银行,两年后本金和利息共获1077.44元,则这种存款的年利率是多少?(注:所获利息应扣除5%的利息税,).
23.小红根据学习轴对称的经验,发现其中线段之间、角之间存在着紧密的联系.他以等腰三角形为背景展开了拓展探究.如图①,在等腰直角三角形中,,,点D直线右侧的一动点.作点关于直线的对称点为点,连接,直线与直线交于点,连接,.
(1)【动手操作】
当时,根据题意,在图①上画出图形,
在不添加辅助线和字母的前提下直接写出两对你认为相等的角,
第一对相等的角:____________,第二对相等的角____________;
(2)【问题探究】
根据(1)所画图形,猜想的大小以及,,的数量关系,并说明理由;
(3)【拓展延伸】
如图②,在等腰三角形中,,,其余条件不变,如图②,当时,若,,请继续研究并求的值.
24.如图,在正方形ABCD中,点E是对角线AC上一点,过点E作EF⊥AC,交边AD,AB于点F,H,连接CF,CH.
(1)求证:CF=CH;
(2)若正方形ABCD的边长为1,当△AFH与△CDF的面积相等时,求AE的长.
参考答案:
1.B
2.D
3.B
4.B
5.D
6.B
7.D
8.D
9.A
10.C
11.A
12.A
13.
14.15(1+x)2=21.6
15.19
16.10%
17.
18.(1)
(2)窗框的高是1米,宽是1.5米.
19.(1)45;(2)这两次测试的平均增长率为20%;(3)55%.
20.(1)75,3375
(2)20元
21.投入经费的年平均增长率.
22.4%.
23.(1),,(答案不唯一)
(2),,
(3)
24.(1)略;(2)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
21.3实际问题与一元二次方程
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.为执行国家药品降价政策,给人民群众带来实惠,某药品经过两次降价,每盒零售价由56元降为31.5元,设平均每次降价的百分率是x,则根据题意,下列方程正确的是( )
A.56(1﹣2x)=31.5 B.56(1﹣x)2=31.5
C.31.5(1+x)2=56 D.31.5(1+2x)=56
2.从正方形铁片,截去宽的一条长方形,余下的矩形的面积是,则原来的正方形铁片的面积是( )
A. B. C. D.
3.某经济开发区今年一月份工业产值达到80亿元,第一季度总产值为275亿元,问二、三月平均每月的增长率是多少?设平均每月的增长率为x,根据题意所列方程是( )
A.80(1+x)2=275 B.80+80(1+x)+80(1+x)2=275
C.80(1+x)3=275 D.80(1+x)+80(1+x)2=275
4.某公司员工2018年的人均年收入为18万元,2020年的人均年收入为23万元,设年平均增长率为x,根据题意,可列出方程为( )
A. B.
C. D.
5.《周髀算经》中有一种几何方法可以用来解形如x(x+5)=24的方程的正数解,方法为:如图,将四个长为x+5,宽为x的长方形纸片(面积均为24)拼成一个大正方形,于是大正方形的面积为:24×4+25=121,边长为11,故得x(x+5)=24的正数解为x= ,小明按此方法解关于x的方程x2+mx﹣n=0时,构造出同样的图形.已知大正方形的面积为10,小正方形的面积为4,则( )
A.m=2,n=3 B.m= ,n=2 C.m= ,n=2 D.m=2,n=
6.从一块正方形铁皮上截去2cm宽的一个长方形,余下的面积是48cm2,则原来正方形的面积为( )
A.56cm2 B.64cm2 C.81cm2 D.100cm2
7.按照党中央、国务院决策部署,为了活跃市场主体、助推各地区经济发展,各省市地区抓紧推动稳经济一揽子政策落实落地.江夏区制定了“黄金十条”,坚定企业疫后发展信心,促进企业稳步高效增长.2022年我区某企业4月份的利润是100万元,第二季度的总利润达到500万元,设利润平均月增长率为x,则依题意列方程为( )
A. B.
C. D.
8.电影《流浪地球2》于2023年1月22日在中国上映,第一天票房约4亿,以后每天票房按相同的增长率增长,前三天票房累计约10亿,若把增长率记作x,则方程可以列为( )
A. B.
C. D.
9.《九章算术》是我国古代内容极为丰富的数学名著,其中“勾股”章有一题,大意是:已知矩形门的高比宽多6尺,门的对角线长10尺,那么门的高和宽各是多少?如果设门的宽为x尺.根据题意,所列方程为( )
A. B. C. D.
10.有一块长30m、宽20m的矩形田地,准备修筑同样宽的三条直路(如图),把田地分成六块,种植不同品种的蔬菜,并且种植蔬菜面积为基地面积的.设道路的宽度为m,下列方程:①;②;③.其中正确的是( )
A.①② B.①③ C.②③ D.③
11.“读书可以让人保持思想活力,让人得到智慧启发,让人滋养浩然之气”某校为响应我市全民阅读活动,利用节假日面向社会开放学校图书馆.据统计,第一个月进馆324人次,进馆人次逐月增加,第三个月进馆1600人次.若进馆人次的月平均增长率为x,由题意可列方程( )
A. B.
C. D.
12.某口罩经销商批发了一批口罩,进货单价为每盒50元,若按每盒60元出售,则每周可销售80盒.现准备提价销售,经市场调研发现:每盒每提价1元,每周销量就会减少2盒,为保护消费者利益,物价部门规定,销售时利润率不能超过50%,设该口罩售价为每盒元,现在预算销售这种口罩每周要获得1200元利润,则每盒口罩的售价应定为( )
A.70元 B.80元 C.70元或80元 D.75元
二、填空题
13.如图,将面积为25的正方形的边的长度增加,变为面积为22的矩形.若正方形和矩形的周长相等,则的值是 .
14.随着居民经济收入的不断提高以及汽车业的快速发展,家用汽车已越来越多地进入普通家庭.抽样调查显示,截止至2020年底某市汽车拥有量为21.6万辆,已知2018年底该市汽车拥有量为15万辆,设2018年底至2020年底该市汽车拥有量的年平均增长率为,根据题意列方程得 .
15.有一个人患了流感,经过两轮传染后得知共传染400人,如果每轮传染率都相同,那么每轮传染中平均一个人传染了 个人
16.某市某楼盘准备以每平方米7200元的均价对外销售,由于国务院有关房地产的新政策出台后,购房者持币观望,为了加快资金周转,房地产开发商对价格经过两次下调后,决定以每平方米5832元的均价开盘销售.则平均每次下调的百分率为 .
17.同学聚会,每两人都握手一次,共握手45次,设x人参加聚会,可列方程为 .
三、解答题
18.用长为6米的铅合金条制成如图所示的矩形窗框,其中////,设窗框的高度为米.
(1)设窗框宽度为米,则______米(用含的代数式表示);
(2)当窗户的透光面积为1.5平方米时,请你计算出窗框的高和宽分别是多少米(铝合金条的宽度忽略不计)
19.某单位为了扩大经营,分四次向社会进行招工测试,测试后对成绩合格人数与不合格人数进行统计,并绘制成如图所示的不完整的统计图.
(1)测试不合格人数的中位数是 .
(2)第二次测试合格人数为50人,到第四次测试合格人数为每次测试不合格人数平均数的2倍少18人,若这两次测试的平均增长率相同,求平均增长率;
(3)在(2)的条件下补全条形统计图和扇形统计图.
20.商场销售某种商品,每件进价100元,若每件售价150元,平均每天售出60件.经调查发现:当商品售价每降低1元时,平均每天可多售出3件.
(1)当商品售价降低5元时,每天销售量可达到______件,每天盈利______元.
(2)为了减少库存,每件商品降价多少元时,商场通过销售这种商品每天盈利3600元?
21.近年我市积极推进“智慧校园”建设,加大对学校教育信息化的建设的投入,去年投入2000万元,之后逐步增加投入,按计划明年投入达到2880万元,求投入经费的年平均增长率.
22.某人将1000元人民币按一年期存入银行,到期后将本金和利息再按一年期存入银行,两年后本金和利息共获1077.44元,则这种存款的年利率是多少?(注:所获利息应扣除5%的利息税,).
23.小红根据学习轴对称的经验,发现其中线段之间、角之间存在着紧密的联系.他以等腰三角形为背景展开了拓展探究.如图①,在等腰直角三角形中,,,点D直线右侧的一动点.作点关于直线的对称点为点,连接,直线与直线交于点,连接,.
(1)【动手操作】
当时,根据题意,在图①上画出图形,
在不添加辅助线和字母的前提下直接写出两对你认为相等的角,
第一对相等的角:____________,第二对相等的角____________;
(2)【问题探究】
根据(1)所画图形,猜想的大小以及,,的数量关系,并说明理由;
(3)【拓展延伸】
如图②,在等腰三角形中,,,其余条件不变,如图②,当时,若,,请继续研究并求的值.
24.如图,在正方形ABCD中,点E是对角线AC上一点,过点E作EF⊥AC,交边AD,AB于点F,H,连接CF,CH.
(1)求证:CF=CH;
(2)若正方形ABCD的边长为1,当△AFH与△CDF的面积相等时,求AE的长.
参考答案:
1.B
2.D
3.B
4.B
5.D
6.B
7.D
8.D
9.A
10.C
11.A
12.A
13.
14.15(1+x)2=21.6
15.19
16.10%
17.
18.(1)
(2)窗框的高是1米,宽是1.5米.
19.(1)45;(2)这两次测试的平均增长率为20%;(3)55%.
20.(1)75,3375
(2)20元
21.投入经费的年平均增长率.
22.4%.
23.(1),,(答案不唯一)
(2),,
(3)
24.(1)略;(2)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
