24.2 点和圆、直线和圆的位置关系 同步练习 (含答案)人教版数学九年级上册
文档属性
| 名称 | 24.2 点和圆、直线和圆的位置关系 同步练习 (含答案)人教版数学九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 645.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-08 09:09:48 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
24.2点和圆、直线和圆的位置关系
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.在证明“三角形中必有一个内角小于或等于”时先假设每一个内角都大于,然后,…,这种证明方法是( )
A.综合法 B.举反例法 C.数学归纳法 D.反证法
2.下列说法正确的个数是( )
①0.01的立方根是0.000001;
②如果一个角的两边分别平行于另一个角的两边,则两个角一定相等;
③正三角形既是中心对称又是轴对称图形;
④顺次连接对角线相等的四边形四边中点所得的四边形必是矩形;
⑤三角形的内心到三角形的三个顶点的距离相等
A.0个 B.1个 C.2个 D.3个
3.圆外一点P,PA、PB分别切⊙O于A、B,C为优弧AB上一点,若∠ACB=a,则∠APB=( )
A.180°- B.90°- C.90°+ D.180°-2
4.如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D.连接BD,BE,CE,若∠CBD=33°,则∠BEC=( )
A.66° B.114° C.123° D.132°
5.如图,,分别切于,两点,如果,,那么的长为( )
A. B. C. D.
6.下列命题中:①相等的圆心角所对的弧相等;②平分弦的直径垂直于弦;③垂直于半径的直线是圆的切线;④E,F是∠AOB的两边OA,OB上的两点,则不同的E,O,F三点确定一个圆:其中正确的有( )
A.个 B.个 C.个 D.0个
7.如图,为的切线,A,B分别为切点,,点P到圆心O的距离,则的半径为( )
A. B.1 C. D.2
8.如图,是一张三角形的纸片,是它的内切圆,点是其中的一个切点,已知,小明准备用剪刀沿着与相切的任意一条直线剪下一块三角形,则剪下的的周长为( )
A. B. C. D.随直线的变化而变化
9.若的半径为,点A到圆心O的距离为,那么点A与⊙O的位置关系是( )
A.点A在圆外 B.点A在圆上 C.点A在圆内 D.不能确定
10.下列命题中是真命题的是( )
A.平分弦的直径,必垂直于这条弦;
B.圆的切线垂直于圆的半径;
C.从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角
D.同圆中,等弦所对的圆周角相等
11.在平面直角坐标系中,已知点,以原点为圆心,5为半径作,则( )
A.点在上 B.点在内
C.点在外 D.点与的位置关系无法确定
12.用反证法证明“在四边形中,至少有一个内角不大于90°”时,应假设( )
A.四边形中有一个内角小于90° B.四边形中每一个内角都小于90°
C.四边形中有一个内角大于90° D.四边形中每一个内角都大于90°
二、填空题
13.如图,中,,,点在射线上运动,连接交外接圆于,则的最小值为 .
14.在 Rt△ABC 中,AB=6,BC=8,则这个三角形的内切圆的半径是 .
15.三角形的内切圆的圆心是三角形的三条 的交点,它到三角形三边的距离相等.
16.如图,AB是⊙O的直径,BC切⊙O于点B,AC交⊙O于点D.若∠A=30°,AD=2,则BC的为 .
17.如图,中,,圆O是的内切圆,D,E,F是切点.若,则 .
三、解答题
18.【问题提出】用n个圆最多能把平面分成几个区域?
【问题探究】为了解决上面的数学问题,我们采取一般问题特殊化的策略,先从最简单情形入手,再逐次递进,最后猜想得出结论.
探究一:如图1,一个圆能把平面分成2个区域.
探究二:用2个圆最多能把平面分成几个区域?
如图2,在探究一的基础上,为了使分成的区域最多,应使新增加的圆与前1个圆有2个交点,将新增加的圆分成2部分,从而增加2个区域,所以,用2个圆最多能把平面分成4个区域.
探究三:用3个圆最多能把平面分成几个区域?
如图3,在探究二的基础上,为了使分成的区域最多,应使新增加的圆与前2个圆分别有2个交点,将新增加的圆分成部分,从而增加4个区域,所以,用3个圆最多能把平面分成8个区域.
(1)用4个圆最多能把平面分成几个区域?
仿照前面的探究方法,写出解答过程,不需画图.
(2)【一般结论】用n个圆最多能把平面分成几个区域?
为了使分成的区域最多,应使新增加的圆与前个圆分别有2个交点,将新增加的圆分成______________部分,从而增加___________________个区域,所以,用n个圆最多能把平面分成__________________个区域.(将结果进行化简)
(3)【结论应用】
①用10个圆最多能把平面分成_________个区域;
②用___________个圆最多能把平面分成422个区域.
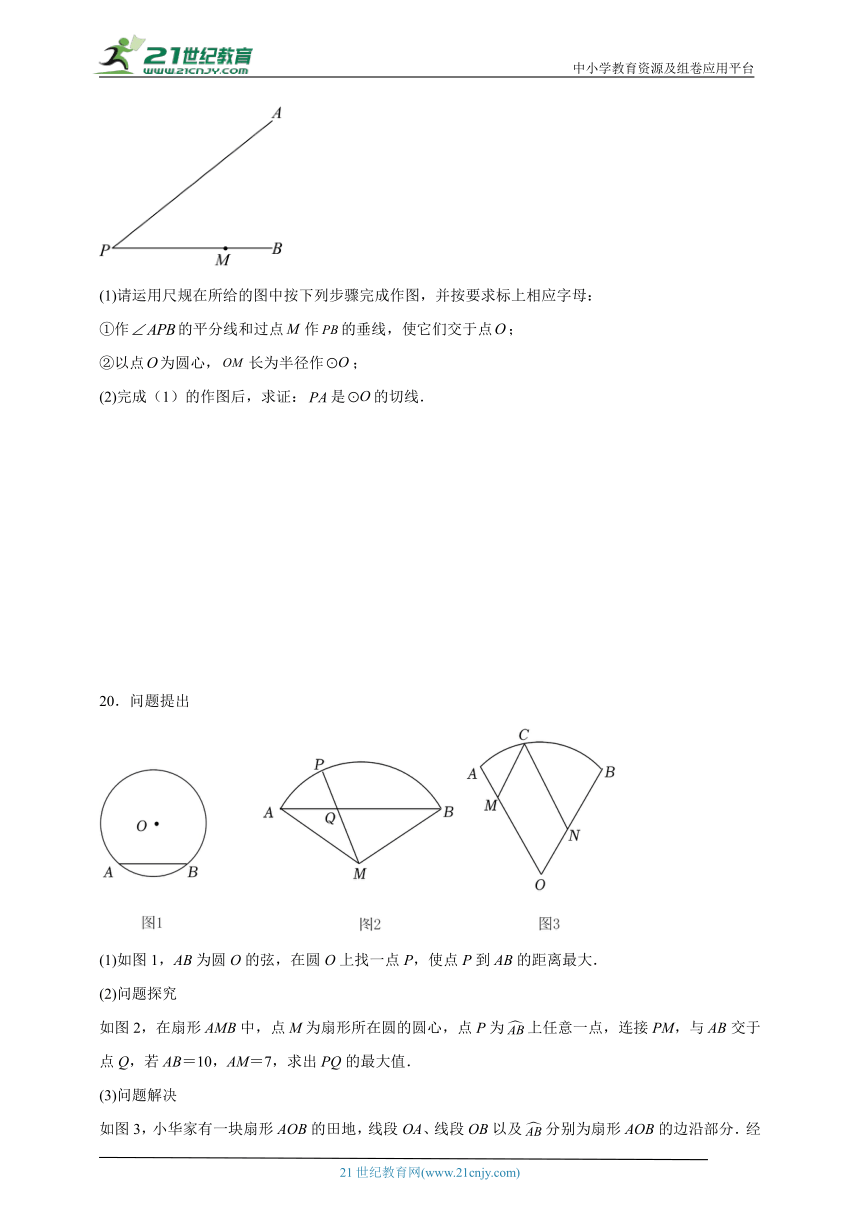
19.如图,已知,点是上的一个定点.
(1)请运用尺规在所给的图中按下列步骤完成作图,并按要求标上相应字母:
①作的平分线和过点作的垂线,使它们交于点;
②以点为圆心,长为半径作;
(2)完成(1)的作图后,求证:是的切线.
20.问题提出
(1)如图1,AB为圆O的弦,在圆O上找一点P,使点P到AB的距离最大.
(2)问题探究
如图2,在扇形AMB中,点M为扇形所在圆的圆心,点P为上任意一点,连接PM,与AB交于点Q,若AB=10,AM=7,求出PQ的最大值.
(3)问题解决
如图3,小华家有一块扇形AOB的田地,线段OA、线段OB以及分别为扇形AOB的边沿部分.经过市场调查发现,小华爸爸打算在扇形AOB的田地中圈出一片空地用作种植当季蔬菜,具体操作方式如下:在上选取点C,过点C作CMOB,CNOA,则四边形MONC为小华爸爸所圈空地.已知:扇形AOB的圆心角∠AOB=60°,OA=OB=90m,且用于修建围挡的线段MC部分与线段CN部分的成本均为30元/米.请你根据以上数据计算:小华爸爸最终所花费的修建费预算最多是多少元?(即求出CM+CN的最大值)(结果保留整数,取1.73)
21.如图,在矩形中,,,P是边上一点,过点A、B、P、作
(1)圆心O在上吗?为什么?
(2)当时,判断与的位置关系;
(3)当与相切时,求被截得的弦长.
22.要对一块长60米、宽40米的矩形荒地进行绿化和硬化.
(1)设计方案如图①所示,矩形P、Q为两块绿地,其余为硬化路面,P、Q两块绿地周围的硬化路面宽都相等,并使两块绿地面积的和为矩形面积的,求P、Q两块绿地周围的硬化路面的宽.
(2)某同学有如下设想:设计绿化区域为相外切的两等圆,圆心分别为和,且到的距离与到的距离都相等,其余为硬化地面,如图②所示,这个设想是否成立?若成立,求出圆的半径;若不成立,说明理由.
23.已知:如图,直线,被所截,,是同位角,且.求证:不平行于.
24.已知的三边长分别为,Ⅰ为的内心,且Ⅰ在的边上的射影分别为.
(1)若,求内切圆半径r;
(2)求证:.
参考答案:
1.D
2.A
3.D
4.C
5.B
6.D
7.B
8.C
9.A
10.C
11.A
12.D
13.1
14.2 或-1.
15.角平分线
16.
17.1
18.(1)在探究三的基础上,为了使分成的区域最多,应使新增加的圆与前3个圆分别有2个交点,将新增的圆分成部分,从而增加6个区域,所以,用4个圆最多能把平面分成14个区域;(2);;;(3)①92;②21
19.略
20.(1)略
(2)
(3)210元
21.(1)圆心O在上
(2)与相离
(3)
22.(1)10米
(2)设想成立,10米
23.略
24.(1)1;(2)略
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
24.2点和圆、直线和圆的位置关系
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.在证明“三角形中必有一个内角小于或等于”时先假设每一个内角都大于,然后,…,这种证明方法是( )
A.综合法 B.举反例法 C.数学归纳法 D.反证法
2.下列说法正确的个数是( )
①0.01的立方根是0.000001;
②如果一个角的两边分别平行于另一个角的两边,则两个角一定相等;
③正三角形既是中心对称又是轴对称图形;
④顺次连接对角线相等的四边形四边中点所得的四边形必是矩形;
⑤三角形的内心到三角形的三个顶点的距离相等
A.0个 B.1个 C.2个 D.3个
3.圆外一点P,PA、PB分别切⊙O于A、B,C为优弧AB上一点,若∠ACB=a,则∠APB=( )
A.180°- B.90°- C.90°+ D.180°-2
4.如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D.连接BD,BE,CE,若∠CBD=33°,则∠BEC=( )
A.66° B.114° C.123° D.132°
5.如图,,分别切于,两点,如果,,那么的长为( )
A. B. C. D.
6.下列命题中:①相等的圆心角所对的弧相等;②平分弦的直径垂直于弦;③垂直于半径的直线是圆的切线;④E,F是∠AOB的两边OA,OB上的两点,则不同的E,O,F三点确定一个圆:其中正确的有( )
A.个 B.个 C.个 D.0个
7.如图,为的切线,A,B分别为切点,,点P到圆心O的距离,则的半径为( )
A. B.1 C. D.2
8.如图,是一张三角形的纸片,是它的内切圆,点是其中的一个切点,已知,小明准备用剪刀沿着与相切的任意一条直线剪下一块三角形,则剪下的的周长为( )
A. B. C. D.随直线的变化而变化
9.若的半径为,点A到圆心O的距离为,那么点A与⊙O的位置关系是( )
A.点A在圆外 B.点A在圆上 C.点A在圆内 D.不能确定
10.下列命题中是真命题的是( )
A.平分弦的直径,必垂直于这条弦;
B.圆的切线垂直于圆的半径;
C.从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角
D.同圆中,等弦所对的圆周角相等
11.在平面直角坐标系中,已知点,以原点为圆心,5为半径作,则( )
A.点在上 B.点在内
C.点在外 D.点与的位置关系无法确定
12.用反证法证明“在四边形中,至少有一个内角不大于90°”时,应假设( )
A.四边形中有一个内角小于90° B.四边形中每一个内角都小于90°
C.四边形中有一个内角大于90° D.四边形中每一个内角都大于90°
二、填空题
13.如图,中,,,点在射线上运动,连接交外接圆于,则的最小值为 .
14.在 Rt△ABC 中,AB=6,BC=8,则这个三角形的内切圆的半径是 .
15.三角形的内切圆的圆心是三角形的三条 的交点,它到三角形三边的距离相等.
16.如图,AB是⊙O的直径,BC切⊙O于点B,AC交⊙O于点D.若∠A=30°,AD=2,则BC的为 .
17.如图,中,,圆O是的内切圆,D,E,F是切点.若,则 .
三、解答题
18.【问题提出】用n个圆最多能把平面分成几个区域?
【问题探究】为了解决上面的数学问题,我们采取一般问题特殊化的策略,先从最简单情形入手,再逐次递进,最后猜想得出结论.
探究一:如图1,一个圆能把平面分成2个区域.
探究二:用2个圆最多能把平面分成几个区域?
如图2,在探究一的基础上,为了使分成的区域最多,应使新增加的圆与前1个圆有2个交点,将新增加的圆分成2部分,从而增加2个区域,所以,用2个圆最多能把平面分成4个区域.
探究三:用3个圆最多能把平面分成几个区域?
如图3,在探究二的基础上,为了使分成的区域最多,应使新增加的圆与前2个圆分别有2个交点,将新增加的圆分成部分,从而增加4个区域,所以,用3个圆最多能把平面分成8个区域.
(1)用4个圆最多能把平面分成几个区域?
仿照前面的探究方法,写出解答过程,不需画图.
(2)【一般结论】用n个圆最多能把平面分成几个区域?
为了使分成的区域最多,应使新增加的圆与前个圆分别有2个交点,将新增加的圆分成______________部分,从而增加___________________个区域,所以,用n个圆最多能把平面分成__________________个区域.(将结果进行化简)
(3)【结论应用】
①用10个圆最多能把平面分成_________个区域;
②用___________个圆最多能把平面分成422个区域.
19.如图,已知,点是上的一个定点.
(1)请运用尺规在所给的图中按下列步骤完成作图,并按要求标上相应字母:
①作的平分线和过点作的垂线,使它们交于点;
②以点为圆心,长为半径作;
(2)完成(1)的作图后,求证:是的切线.
20.问题提出
(1)如图1,AB为圆O的弦,在圆O上找一点P,使点P到AB的距离最大.
(2)问题探究
如图2,在扇形AMB中,点M为扇形所在圆的圆心,点P为上任意一点,连接PM,与AB交于点Q,若AB=10,AM=7,求出PQ的最大值.
(3)问题解决
如图3,小华家有一块扇形AOB的田地,线段OA、线段OB以及分别为扇形AOB的边沿部分.经过市场调查发现,小华爸爸打算在扇形AOB的田地中圈出一片空地用作种植当季蔬菜,具体操作方式如下:在上选取点C,过点C作CMOB,CNOA,则四边形MONC为小华爸爸所圈空地.已知:扇形AOB的圆心角∠AOB=60°,OA=OB=90m,且用于修建围挡的线段MC部分与线段CN部分的成本均为30元/米.请你根据以上数据计算:小华爸爸最终所花费的修建费预算最多是多少元?(即求出CM+CN的最大值)(结果保留整数,取1.73)
21.如图,在矩形中,,,P是边上一点,过点A、B、P、作
(1)圆心O在上吗?为什么?
(2)当时,判断与的位置关系;
(3)当与相切时,求被截得的弦长.
22.要对一块长60米、宽40米的矩形荒地进行绿化和硬化.
(1)设计方案如图①所示,矩形P、Q为两块绿地,其余为硬化路面,P、Q两块绿地周围的硬化路面宽都相等,并使两块绿地面积的和为矩形面积的,求P、Q两块绿地周围的硬化路面的宽.
(2)某同学有如下设想:设计绿化区域为相外切的两等圆,圆心分别为和,且到的距离与到的距离都相等,其余为硬化地面,如图②所示,这个设想是否成立?若成立,求出圆的半径;若不成立,说明理由.
23.已知:如图,直线,被所截,,是同位角,且.求证:不平行于.
24.已知的三边长分别为,Ⅰ为的内心,且Ⅰ在的边上的射影分别为.
(1)若,求内切圆半径r;
(2)求证:.
参考答案:
1.D
2.A
3.D
4.C
5.B
6.D
7.B
8.C
9.A
10.C
11.A
12.D
13.1
14.2 或-1.
15.角平分线
16.
17.1
18.(1)在探究三的基础上,为了使分成的区域最多,应使新增加的圆与前3个圆分别有2个交点,将新增的圆分成部分,从而增加6个区域,所以,用4个圆最多能把平面分成14个区域;(2);;;(3)①92;②21
19.略
20.(1)略
(2)
(3)210元
21.(1)圆心O在上
(2)与相离
(3)
22.(1)10米
(2)设想成立,10米
23.略
24.(1)1;(2)略
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
