1.3探索三角形全等的条件 苏科版初中数学八年级上册同步练习(含详细答案解析)
文档属性
| 名称 | 1.3探索三角形全等的条件 苏科版初中数学八年级上册同步练习(含详细答案解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 493.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-07 10:46:42 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
1.3探索三角形全等的条件苏科版初中数学八年级上册同步练习
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.如图,点在上,点在上,且,那么补充下列一个条件后,仍无法判定≌的是( )
A. B. C. D.
2.如图,和均为等腰直角三角形,,,,三点在同一条直线上,连接,现有以下结论:;;;;;其中正确的个数是 ( )
A. B. C. D.
3.如图,为的平分线,作垂直于,的面积为,则的面积为( )
A. B. C. D.
4.如图,已知,,,是上的两点,,若,,,则的长为 ( )
A. B. C. D.
5.如图,在中,,是高和的交点.若,则的长是 ( )
A. B. C. D.
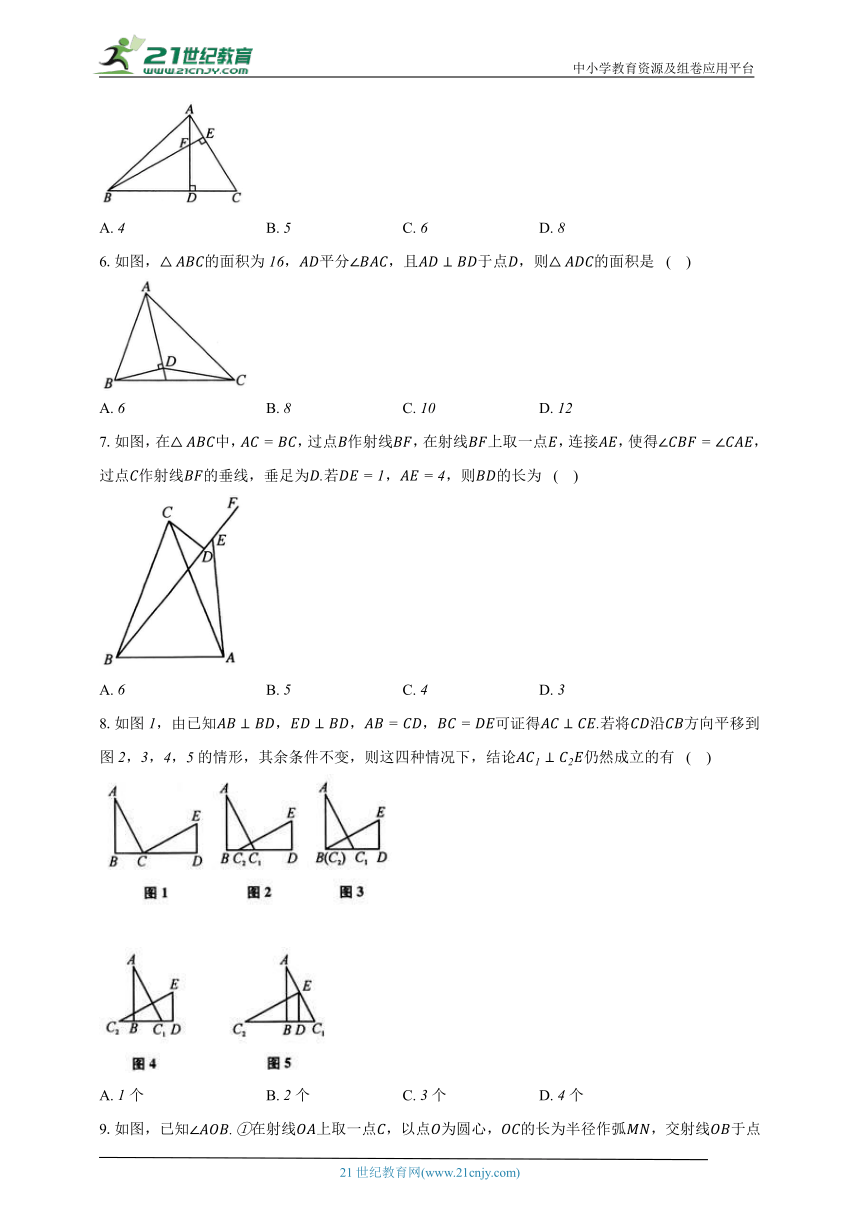
6.如图,的面积为,平分,且于点,则的面积是 ( )
A. B. C. D.
7.如图,在中,,过点作射线,在射线上取一点,连接,使得,过点作射线的垂线,垂足为若,,则的长为 ( )
A. B. C. D.
8.如图,由已知,,,可证得若将沿方向平移到图,,,的情形,其余条件不变,则这四种情况下,结论仍然成立的有 ( )
A. 个 B. 个 C. 个 D. 个
9.如图,已知在射线上取一点,以点为圆心,的长为半径作弧,交射线于点,连接;分别以点,为圆心,的长为半径作弧,两弧交于点,连接,;作射线,交于点根据以上作图过程及所作图形,下列结论错误的是 ( )
A. B.
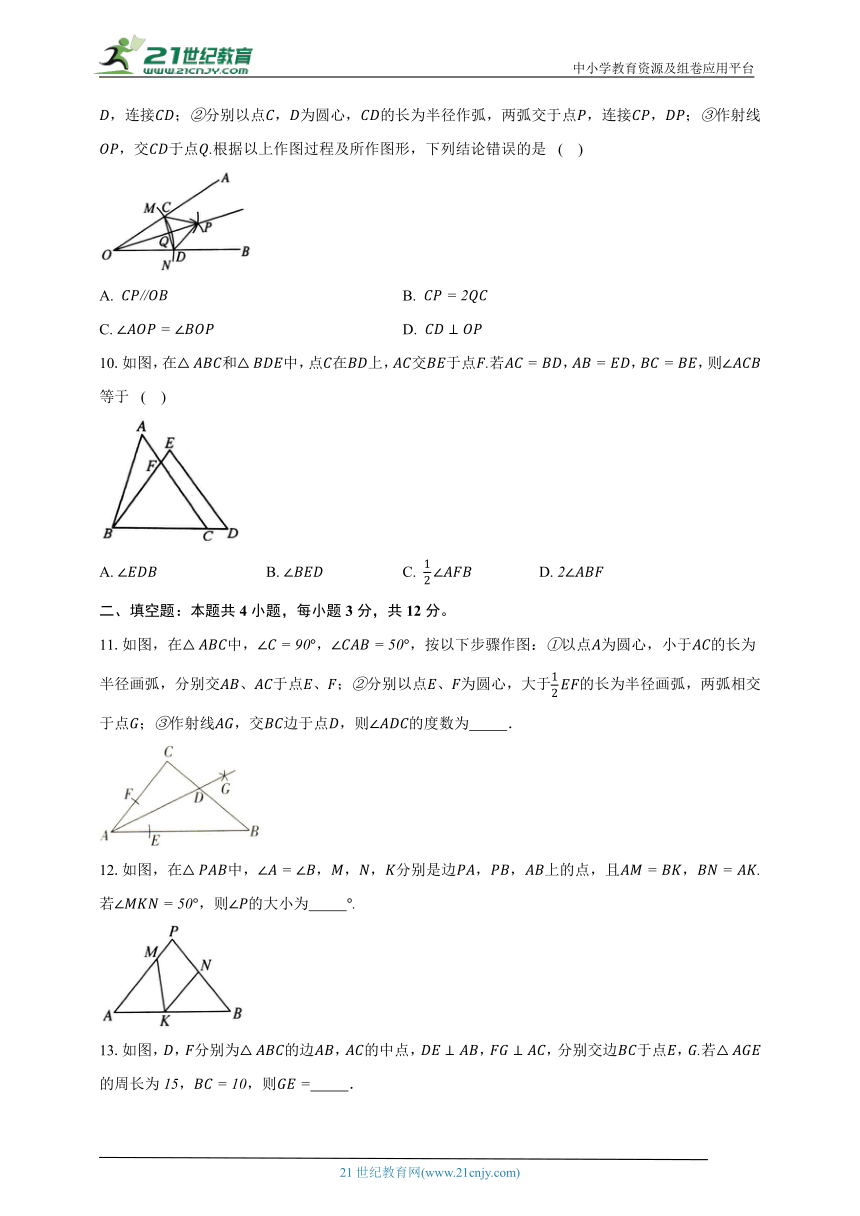
C. D.
10.如图,在和中,点在上,交于点若,,,则等于 ( )
A. B. C. D.
二、填空题:本题共4小题,每小题3分,共12分。
11.如图,在中,,,按以下步骤作图:以点为圆心,小于的长为半径画弧,分别交、于点、;分别以点、为圆心,大于的长为半径画弧,两弧相交于点;作射线,交边于点,则的度数为 .
12.如图,在中,,,,分别是边,,上的点,且,若,则的大小为
13.如图,,分别为的边,的中点,,,分别交边于点,若的周长为,,则 .
14.如图,在和中,,,,且点,,在同一直线上,点,在同侧,连接,交于点若,则 .
三、解答题:本题共6小题,共48分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
如图,点在线段上,在和中,,,.
求证:.
16.本小题分
如图,在和中,延长交于点,,,求证:.
17.本小题分
如图,,,,垂足分别为、,求证:.
18.本小题分
如图,已知在中,于点,于点,是线段上一点,,是线段的延长线上一点,,连接,.
证明:;
猜想线段与之间的数量和位置关系,并说明理由.
19.本小题分
如图,在和中,,,,点,,在一条直线上,连接.
求证:≌;
试猜想与之间的位置关系,并给出证明.
20.本小题分
如图,,,求证:
;
.
答案和解析
1.【答案】
【解析】【分析】
根据全等三角形的判定方法一一判断即可.
本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:、、、、.
注意:、不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
【解答】
解:由图形可知,
A、根据能推出≌,故本选项不符合题意;
B、没有边的条件,不能推出≌,故本选项符合题意;
C、根据能推出≌,正确,故本选项不符合题意;
D、根据能推出≌,正确,故本选项不符合题意;
故选:.
2.【答案】
【解析】提示:易证≌,所以,因为和均为等腰直角三角形,所以,,所以,所以,所以,即,所以,故正确.因为,所以,故选项正确.过点作于点,由题可知,不一定等于,所以不一定等于,即不一定等于,故错误.
3.【答案】
【解析】延长交于点,
为的平分线,
.
,
.
,
≌,
,
,,
,
.
的面积为,
故选B.
4.【答案】
【解析】提示:因为,所以因为,所以所以因为,,所以又因为,所以≌,所以,所以.
5.【答案】
【解析】提示:因为是高和的交点,所以,所以,因为,所以易证≌,所以.
6.【答案】
【解析】提示:延长交于点因为平分,,所以,又因为为公共边,所以≌,所以,所以,,所以.
7.【答案】
【解析】提示:连接,过点作,交的延长线于点因为,,所以易证≌,所以,易证≌,所以所以.
8.【答案】
【解析】略
9.【答案】
【解析】略
10.【答案】
【解析】提示:易证≌,所以因为是的外角,所以所以.
11.【答案】
【解析】略
12.【答案】
【解析】提示:易证≌,所以,因为,所以,又因为,所以,所以.
13.【答案】
【解析】提示:易证≌,≌,所以,因为的周长为,所以所以,即因为,所以,所以.
14.【答案】
【解析】提示:易证≌,所以,所以因为,所以,所以.
15.【答案】解:在和中,
,
≌,
.
【解析】由两个三角形的全等判定直接可判断两个三角形全等,得出结论.
本题考查了三角形全等的判定与性质,掌握判定两个三角形全等的方法是解题的关键.
16.【答案】证明:,
,
在和中,
,
≌,
.
【解析】由“”可证≌,可得结论.
本题考查了全等三角形的判定和性质,证明三角形全等是解题的关键.
17.【答案】证明:,,
.
和均是直角三角形.
,
,即.
在和中,
.
D.
【解析】见答案.
18.【答案】【小题】
解:因为,,所以,所以,所以.
【小题】
,理由如下: 在和中,因为,,,所以≌,所以,因为,所以,所以,即.
【解析】 略
略
19.【答案】【小题】
证明:因为,所以在和中,所以≌.
【小题】
解:证明如下: 因为≌,所以因为,所以所以,即,所以.
【解析】 略
略
20.【答案】【小题】
证明:在和中,所以≌,所以.
【小题】
因为,所以由,得≌,所以在和中,所以≌,所以.
【解析】 略
略
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
1.3探索三角形全等的条件苏科版初中数学八年级上册同步练习
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.如图,点在上,点在上,且,那么补充下列一个条件后,仍无法判定≌的是( )
A. B. C. D.
2.如图,和均为等腰直角三角形,,,,三点在同一条直线上,连接,现有以下结论:;;;;;其中正确的个数是 ( )
A. B. C. D.
3.如图,为的平分线,作垂直于,的面积为,则的面积为( )
A. B. C. D.
4.如图,已知,,,是上的两点,,若,,,则的长为 ( )
A. B. C. D.
5.如图,在中,,是高和的交点.若,则的长是 ( )
A. B. C. D.
6.如图,的面积为,平分,且于点,则的面积是 ( )
A. B. C. D.
7.如图,在中,,过点作射线,在射线上取一点,连接,使得,过点作射线的垂线,垂足为若,,则的长为 ( )
A. B. C. D.
8.如图,由已知,,,可证得若将沿方向平移到图,,,的情形,其余条件不变,则这四种情况下,结论仍然成立的有 ( )
A. 个 B. 个 C. 个 D. 个
9.如图,已知在射线上取一点,以点为圆心,的长为半径作弧,交射线于点,连接;分别以点,为圆心,的长为半径作弧,两弧交于点,连接,;作射线,交于点根据以上作图过程及所作图形,下列结论错误的是 ( )
A. B.
C. D.
10.如图,在和中,点在上,交于点若,,,则等于 ( )
A. B. C. D.
二、填空题:本题共4小题,每小题3分,共12分。
11.如图,在中,,,按以下步骤作图:以点为圆心,小于的长为半径画弧,分别交、于点、;分别以点、为圆心,大于的长为半径画弧,两弧相交于点;作射线,交边于点,则的度数为 .
12.如图,在中,,,,分别是边,,上的点,且,若,则的大小为
13.如图,,分别为的边,的中点,,,分别交边于点,若的周长为,,则 .
14.如图,在和中,,,,且点,,在同一直线上,点,在同侧,连接,交于点若,则 .
三、解答题:本题共6小题,共48分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
如图,点在线段上,在和中,,,.
求证:.
16.本小题分
如图,在和中,延长交于点,,,求证:.
17.本小题分
如图,,,,垂足分别为、,求证:.
18.本小题分
如图,已知在中,于点,于点,是线段上一点,,是线段的延长线上一点,,连接,.
证明:;
猜想线段与之间的数量和位置关系,并说明理由.
19.本小题分
如图,在和中,,,,点,,在一条直线上,连接.
求证:≌;
试猜想与之间的位置关系,并给出证明.
20.本小题分
如图,,,求证:
;
.
答案和解析
1.【答案】
【解析】【分析】
根据全等三角形的判定方法一一判断即可.
本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:、、、、.
注意:、不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
【解答】
解:由图形可知,
A、根据能推出≌,故本选项不符合题意;
B、没有边的条件,不能推出≌,故本选项符合题意;
C、根据能推出≌,正确,故本选项不符合题意;
D、根据能推出≌,正确,故本选项不符合题意;
故选:.
2.【答案】
【解析】提示:易证≌,所以,因为和均为等腰直角三角形,所以,,所以,所以,所以,即,所以,故正确.因为,所以,故选项正确.过点作于点,由题可知,不一定等于,所以不一定等于,即不一定等于,故错误.
3.【答案】
【解析】延长交于点,
为的平分线,
.
,
.
,
≌,
,
,,
,
.
的面积为,
故选B.
4.【答案】
【解析】提示:因为,所以因为,所以所以因为,,所以又因为,所以≌,所以,所以.
5.【答案】
【解析】提示:因为是高和的交点,所以,所以,因为,所以易证≌,所以.
6.【答案】
【解析】提示:延长交于点因为平分,,所以,又因为为公共边,所以≌,所以,所以,,所以.
7.【答案】
【解析】提示:连接,过点作,交的延长线于点因为,,所以易证≌,所以,易证≌,所以所以.
8.【答案】
【解析】略
9.【答案】
【解析】略
10.【答案】
【解析】提示:易证≌,所以因为是的外角,所以所以.
11.【答案】
【解析】略
12.【答案】
【解析】提示:易证≌,所以,因为,所以,又因为,所以,所以.
13.【答案】
【解析】提示:易证≌,≌,所以,因为的周长为,所以所以,即因为,所以,所以.
14.【答案】
【解析】提示:易证≌,所以,所以因为,所以,所以.
15.【答案】解:在和中,
,
≌,
.
【解析】由两个三角形的全等判定直接可判断两个三角形全等,得出结论.
本题考查了三角形全等的判定与性质,掌握判定两个三角形全等的方法是解题的关键.
16.【答案】证明:,
,
在和中,
,
≌,
.
【解析】由“”可证≌,可得结论.
本题考查了全等三角形的判定和性质,证明三角形全等是解题的关键.
17.【答案】证明:,,
.
和均是直角三角形.
,
,即.
在和中,
.
D.
【解析】见答案.
18.【答案】【小题】
解:因为,,所以,所以,所以.
【小题】
,理由如下: 在和中,因为,,,所以≌,所以,因为,所以,所以,即.
【解析】 略
略
19.【答案】【小题】
证明:因为,所以在和中,所以≌.
【小题】
解:证明如下: 因为≌,所以因为,所以所以,即,所以.
【解析】 略
略
20.【答案】【小题】
证明:在和中,所以≌,所以.
【小题】
因为,所以由,得≌,所以在和中,所以≌,所以.
【解析】 略
略
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
