沪科版数学八年级上册 期中检测卷(含答案)
文档属性
| 名称 | 沪科版数学八年级上册 期中检测卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 527.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-07 14:39:54 | ||
图片预览



文档简介
期中检测卷
(时间:120分钟 满分:150分)
题 号 一 二 三 四 五 六 七 八 总分
得 分
一、选择题(本大题共10 小题,每小题4分,满分40 分)
1.在平面直角坐标系中,点所在象限是 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
2.下列各曲线中,不表示y是x的函数的是 ( )
3.下列函数中,y是x的正比例函数的是 ( )
A. y=6x-1
4.函数y=3x-5的图象不经过 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
5.长度分别为1,5,x的三条线段首尾连接能组成一个三角形,则x的值可以是 ( )
A.4 B.5 C.6 D.7
6.函数 中自变量x的取值范围是 ( )
A. x≠2 B. x>2 C. x≥2 D. x>0
7.点 点 是一次函数y=-4x+3 图象上的两个点,且 则y 与y 的大小关系是 ( )
8.已知a,b,c是△ABC的三边,a:b:c=4:5:6,则它们的对应高 的比是( )
A.15:12:10 B.4:5:6
C.6:5:4 D.10:12:15
9.下列命题:①垂直于同一条直线的两直线平行;②三角形的三个内角中,至少有2个锐角;③三角形的中线、角平分线都是线段;④每一个定理都有逆定理.其中正确的有( )
A.4个 B.3 个 C.2个 D.1个
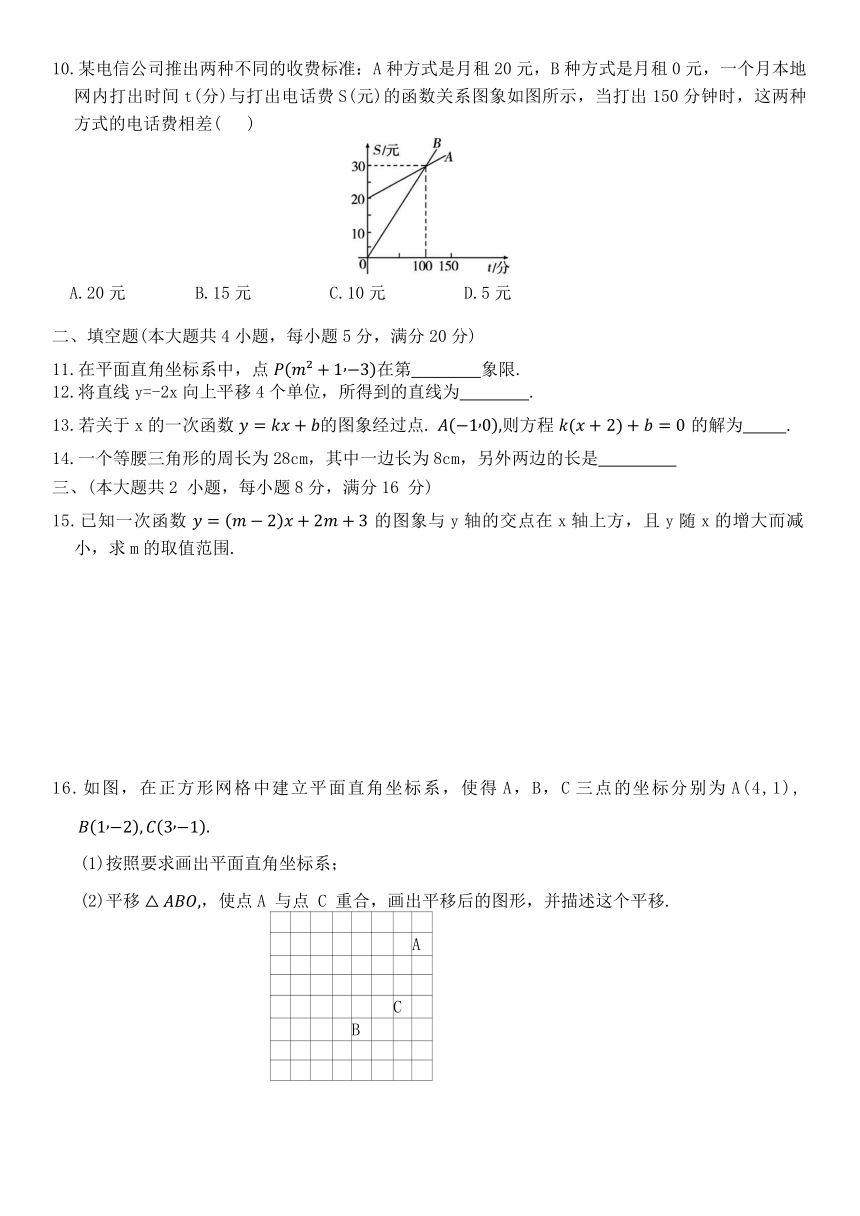
10.某电信公司推出两种不同的收费标准:A种方式是月租20元,B种方式是月租0元,一个月本地网内打出时间t(分)与打出电话费S(元)的函数关系图象如图所示,当打出150分钟时,这两种方式的电话费相差( )
A.20元 B.15元 C.10元 D.5元
二、填空题(本大题共4小题,每小题5分,满分20分)
11.在平面直角坐标系中,点 在第 象限.
12.将直线y=-2x向上平移4个单位,所得到的直线为 .
13.若关于x的一次函数 的图象经过点. 则方程 的解为 .
14.一个等腰三角形的周长为28cm,其中一边长为8cm,另外两边的长是
三、(本大题共2 小题,每小题8分,满分16 分)
15.已知一次函数 的图象与y轴的交点在x轴上方,且y随x的增大而减小,求m的取值范围.
16.如图,在正方形网格中建立平面直角坐标系,使得A,B,C三点的坐标分别为A(4,1),
(1)按照要求画出平面直角坐标系;
(2)平移 ,使点A 与点 C 重合,画出平移后的图形,并描述这个平移.
A
C
B
四、(本大题共2 小题,每小题8分,满分16 分)
17.如图,在平面直角坐标系内,动点 P 按图中箭头所示方向依次运动,第1次从点(0,1)运动到点(1,0),第二次运动到点 ,第3次运动到点(3,0),……按这样的运动规律解决下列问题:
(1)写出动点 P 第10次运动到的点的坐标;
(2)写出动点P第n次运动到的点的坐标.
18.如图,在 中,AD 是 BC 边上的中线, 和 的周长之差为2,且AB 与AC的和为14.若 ,E 是 AD 的中点,求 的面积.
五、(本大题共2 小题,每小题10分,满分20 分)
19.某校举办“诗词大赛”,计划购买甲、乙两种奖品共30件.其中甲种奖品每件30元,乙种奖品每件20 元.
(1)如果购买甲、乙两种奖品共花费800元,那么这两种奖品分别购买了多少件
(2)如果购买乙种奖品的件数不超过甲种奖品件数的2 倍,如何购买甲、乙两种奖品能使得总花费最少
20.如图,在 中,AD平分 点P 为线段AD上的一个点, 交 BC的延长线于点 E.
(1)若 求 的度数;
(2)若 且 求 的度数.
六、(本题满分12分)
21.一个有进水管与出水管的容器,从某时刻开始4分钟内只进水不出水,在随后的8分钟内既进水又出水,12分钟后关闭进水管,放空容器中的水,每分钟的进水量和出水量是两个常数.容器内水量y(单位:升)与时间x(单位:分钟)之间的关系如图所示.
(1)每分钟进水多少升
(2)当 时,求y关于x的函数表达式;
(3)容器中储水量不低于15 升的时长是多少分钟
七、(本题满分12 分)
22.如图,直线 分别与x轴、y轴相交于点 B 和点 C(0,3),与y= 2x交于点A(a,2),点M 在直线OA上.
(1)求直线AB的表达式;
(2)求 的面积;
(3)是否存在点 M,使 的面积与 的面积相等 若存在,求出点 M的坐标;若不存在,说明理由.
八、(本题满分 14 分)
23.在 中,AD 是 的角平分线,AE是 的高.
(1)如图1,若 请计算 的度数;
(2)如图 ,试说明 的数量关系;
(3)如图3,延长AC 到点 F, 和 的角平分线交于点 G,请求出 的度数.
期中检测卷
1. A 2. C 3. D 4. B 5. B 6. A 7. A 8. A 9. C 10. C
11.四 12. y=-2x+4 13. x=-3 14.10cm、10cm或12cm、8cm
15.解:∵一次函数 的图象与y轴的交点在x轴上方, 解得
∵一次函数 的函数值y随x的增大而减小,∴m-2<0.解得m<2.
综合上述,m的取值范围为
16.解:(1)平面直角坐标系如图.
(2)平移后的图形如图.平移方式为向下平移2个单位,向左平移1 个单位.
17.解:(1)由题图可知,动点 P 每运动4次向右平移4个单位.
∴动点 P第10次运动到的点的横坐标为10,纵坐标与第2次运动到的点的纵坐标相同.
∴动点 P第10次运动到的点的坐标为
(2)根据动点 P 的运动规律可知,动点 P 第 n 次运动到的点的坐标为(n,0),(n,-2)或(n,1).
18.解:∵AD 是BC边上的中线,∴BD=CD.
∴△ABD的周长 的周长: 2,即AB-AC=2 ①.
又∵AB+AC=14 ②,①+②,得2AB=16,解得AB=8,∴AC=14-AB=6.
∵AD 是BC边上的中线,E为AD 的中点,
19.解:(1)设甲种奖品购买了x件,乙种奖品购买了y件.
根据题意,得 解得
答:甲种奖品购买了20件,乙种奖品购买了10件.
(2)设购买甲种奖品a件,则购买乙种奖品(30-a)件.
根据题意,得30-a≤3a.解得
∵a为正整数,∴a的最小值为8.
设总花费为 W元,根据题意,得
∵W随a的增大而增大,∴当a=8时,W最小.
∴购买甲种奖品8件,乙种奖品22 件,才能使得总花费最少.
20.解:(1)∵∠B=35°,∠ACB=85°,∠B+∠ACB+∠BAC=180°,∴∠BAC=60°.
∵AD平分∠BAC,∴∠DAC=∠BAD=30°.∴∠PDE=∠B+∠BAD=65°.
又∵PE⊥AD,∴∠DPE=90°.
∵∠PDE+∠DPE+∠E=180°,∴∠E=25°.
(2)∵AD 平分∠BAC,∴∠BAD=∠CAD.
设∠B=α,∵∠B=∠BAD,∴∠BAC=2α.
∵∠B+∠BAC+∠ACB=180°,∠ACB=63°,∴3α+63°=180°.
∴α=39°.∴∠B=∠BAD=39°.∴∠PDC=∠B+∠BAD=78°.
∵EP⊥AD,∴∠EPD=90°.∴∠E=90°-78°=12°.
21.解:(1)根据题意,得4分钟进水20升,则每分钟进水20÷4=5(升).
(2)当4∵图象过(4,20),(12,30),∴ 解得
∴当4(3)根据图象,得每分钟的出水量为 (升).
当0当4≤x≤12时,容器中的储水量不低于15 升;
当x>12时,容器中的储水量不低于15 升的时长是 (分钟).
所以容器中储水量不低于15升的时长是(12+4)-3 =13(分钟).
22.解:(1)∵点A(a,2)在直线y=2x上,∴2=2a.∴a=1.∴点A的坐标为(1,2).
∵直线y=kx+b经过C(0,3)与A(1,2),∴ 解得
∴直线AB的表达式为y=-x+3.
(2)令y=0,得-x+3=0.解得x=3.∴B(3,0).∴OB=3.
∴△OAB的面积
(3)存在点 M,使△OMC的面积与△OAB的面积相等,理由如下:
∵C(0,3),∴OC=3.∴OB=OC=3.
∵△OMC的面积与△OAB的面积相等,
∴M到y轴的距离等于点A的纵坐标.
∴ 点M 的横坐标为2或-2.
当点 M的横坐标为2时,
将x=2代入y=2x,得y=4,则点M的坐标为(2,4).
当点 M 的横坐标为-2时,
将x=-2代入y=2x,得y=-4,则点M的坐标为( -2,-4).
综上所述,点M的坐标为(2,4)或( -2,-4).
23.解:(1)∵∠B=40°,∠C=60°,∠BAC+∠B+∠C=180°,∴∠BAC=80°.
∵AE是△ABC的高,∴∠AEC=90°.∵∠C=60°,∴∠CAE=90°-60°=30°.
∵AD 是∠BAC的角平分线,
∴∠DAE=∠CAD-∠CAE=10°.
(2)∵∠BAC+∠B+∠C=180°.∴∠BAC=180°-∠B-∠C.
∵AE是△ABC的高,∴∠AEC=90°,∴∠CAE=90°-∠C.
∵AD 是∠BAC的角平分线,
即
(3)∵∠CAE和∠BCF的角平分线交于点G,
∴∠CAE=2∠CAG,∠FCB=2∠FCG.
∵∠CAE=∠FCB-∠AEC,∠CAG=∠FCG-∠G,
∴2∠FCG--∠AEC=2(∠FCG--∠G)=2∠FCG-2∠G,即∠AEC=2∠G.
∵AE是△ABC的高,∴∠AEC=90°.∴∠G=45°.
(时间:120分钟 满分:150分)
题 号 一 二 三 四 五 六 七 八 总分
得 分
一、选择题(本大题共10 小题,每小题4分,满分40 分)
1.在平面直角坐标系中,点所在象限是 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
2.下列各曲线中,不表示y是x的函数的是 ( )
3.下列函数中,y是x的正比例函数的是 ( )
A. y=6x-1
4.函数y=3x-5的图象不经过 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
5.长度分别为1,5,x的三条线段首尾连接能组成一个三角形,则x的值可以是 ( )
A.4 B.5 C.6 D.7
6.函数 中自变量x的取值范围是 ( )
A. x≠2 B. x>2 C. x≥2 D. x>0
7.点 点 是一次函数y=-4x+3 图象上的两个点,且 则y 与y 的大小关系是 ( )
8.已知a,b,c是△ABC的三边,a:b:c=4:5:6,则它们的对应高 的比是( )
A.15:12:10 B.4:5:6
C.6:5:4 D.10:12:15
9.下列命题:①垂直于同一条直线的两直线平行;②三角形的三个内角中,至少有2个锐角;③三角形的中线、角平分线都是线段;④每一个定理都有逆定理.其中正确的有( )
A.4个 B.3 个 C.2个 D.1个
10.某电信公司推出两种不同的收费标准:A种方式是月租20元,B种方式是月租0元,一个月本地网内打出时间t(分)与打出电话费S(元)的函数关系图象如图所示,当打出150分钟时,这两种方式的电话费相差( )
A.20元 B.15元 C.10元 D.5元
二、填空题(本大题共4小题,每小题5分,满分20分)
11.在平面直角坐标系中,点 在第 象限.
12.将直线y=-2x向上平移4个单位,所得到的直线为 .
13.若关于x的一次函数 的图象经过点. 则方程 的解为 .
14.一个等腰三角形的周长为28cm,其中一边长为8cm,另外两边的长是
三、(本大题共2 小题,每小题8分,满分16 分)
15.已知一次函数 的图象与y轴的交点在x轴上方,且y随x的增大而减小,求m的取值范围.
16.如图,在正方形网格中建立平面直角坐标系,使得A,B,C三点的坐标分别为A(4,1),
(1)按照要求画出平面直角坐标系;
(2)平移 ,使点A 与点 C 重合,画出平移后的图形,并描述这个平移.
A
C
B
四、(本大题共2 小题,每小题8分,满分16 分)
17.如图,在平面直角坐标系内,动点 P 按图中箭头所示方向依次运动,第1次从点(0,1)运动到点(1,0),第二次运动到点 ,第3次运动到点(3,0),……按这样的运动规律解决下列问题:
(1)写出动点 P 第10次运动到的点的坐标;
(2)写出动点P第n次运动到的点的坐标.
18.如图,在 中,AD 是 BC 边上的中线, 和 的周长之差为2,且AB 与AC的和为14.若 ,E 是 AD 的中点,求 的面积.
五、(本大题共2 小题,每小题10分,满分20 分)
19.某校举办“诗词大赛”,计划购买甲、乙两种奖品共30件.其中甲种奖品每件30元,乙种奖品每件20 元.
(1)如果购买甲、乙两种奖品共花费800元,那么这两种奖品分别购买了多少件
(2)如果购买乙种奖品的件数不超过甲种奖品件数的2 倍,如何购买甲、乙两种奖品能使得总花费最少
20.如图,在 中,AD平分 点P 为线段AD上的一个点, 交 BC的延长线于点 E.
(1)若 求 的度数;
(2)若 且 求 的度数.
六、(本题满分12分)
21.一个有进水管与出水管的容器,从某时刻开始4分钟内只进水不出水,在随后的8分钟内既进水又出水,12分钟后关闭进水管,放空容器中的水,每分钟的进水量和出水量是两个常数.容器内水量y(单位:升)与时间x(单位:分钟)之间的关系如图所示.
(1)每分钟进水多少升
(2)当 时,求y关于x的函数表达式;
(3)容器中储水量不低于15 升的时长是多少分钟
七、(本题满分12 分)
22.如图,直线 分别与x轴、y轴相交于点 B 和点 C(0,3),与y= 2x交于点A(a,2),点M 在直线OA上.
(1)求直线AB的表达式;
(2)求 的面积;
(3)是否存在点 M,使 的面积与 的面积相等 若存在,求出点 M的坐标;若不存在,说明理由.
八、(本题满分 14 分)
23.在 中,AD 是 的角平分线,AE是 的高.
(1)如图1,若 请计算 的度数;
(2)如图 ,试说明 的数量关系;
(3)如图3,延长AC 到点 F, 和 的角平分线交于点 G,请求出 的度数.
期中检测卷
1. A 2. C 3. D 4. B 5. B 6. A 7. A 8. A 9. C 10. C
11.四 12. y=-2x+4 13. x=-3 14.10cm、10cm或12cm、8cm
15.解:∵一次函数 的图象与y轴的交点在x轴上方, 解得
∵一次函数 的函数值y随x的增大而减小,∴m-2<0.解得m<2.
综合上述,m的取值范围为
16.解:(1)平面直角坐标系如图.
(2)平移后的图形如图.平移方式为向下平移2个单位,向左平移1 个单位.
17.解:(1)由题图可知,动点 P 每运动4次向右平移4个单位.
∴动点 P第10次运动到的点的横坐标为10,纵坐标与第2次运动到的点的纵坐标相同.
∴动点 P第10次运动到的点的坐标为
(2)根据动点 P 的运动规律可知,动点 P 第 n 次运动到的点的坐标为(n,0),(n,-2)或(n,1).
18.解:∵AD 是BC边上的中线,∴BD=CD.
∴△ABD的周长 的周长: 2,即AB-AC=2 ①.
又∵AB+AC=14 ②,①+②,得2AB=16,解得AB=8,∴AC=14-AB=6.
∵AD 是BC边上的中线,E为AD 的中点,
19.解:(1)设甲种奖品购买了x件,乙种奖品购买了y件.
根据题意,得 解得
答:甲种奖品购买了20件,乙种奖品购买了10件.
(2)设购买甲种奖品a件,则购买乙种奖品(30-a)件.
根据题意,得30-a≤3a.解得
∵a为正整数,∴a的最小值为8.
设总花费为 W元,根据题意,得
∵W随a的增大而增大,∴当a=8时,W最小.
∴购买甲种奖品8件,乙种奖品22 件,才能使得总花费最少.
20.解:(1)∵∠B=35°,∠ACB=85°,∠B+∠ACB+∠BAC=180°,∴∠BAC=60°.
∵AD平分∠BAC,∴∠DAC=∠BAD=30°.∴∠PDE=∠B+∠BAD=65°.
又∵PE⊥AD,∴∠DPE=90°.
∵∠PDE+∠DPE+∠E=180°,∴∠E=25°.
(2)∵AD 平分∠BAC,∴∠BAD=∠CAD.
设∠B=α,∵∠B=∠BAD,∴∠BAC=2α.
∵∠B+∠BAC+∠ACB=180°,∠ACB=63°,∴3α+63°=180°.
∴α=39°.∴∠B=∠BAD=39°.∴∠PDC=∠B+∠BAD=78°.
∵EP⊥AD,∴∠EPD=90°.∴∠E=90°-78°=12°.
21.解:(1)根据题意,得4分钟进水20升,则每分钟进水20÷4=5(升).
(2)当4
∴当4
当0
当x>12时,容器中的储水量不低于15 升的时长是 (分钟).
所以容器中储水量不低于15升的时长是(12+4)-3 =13(分钟).
22.解:(1)∵点A(a,2)在直线y=2x上,∴2=2a.∴a=1.∴点A的坐标为(1,2).
∵直线y=kx+b经过C(0,3)与A(1,2),∴ 解得
∴直线AB的表达式为y=-x+3.
(2)令y=0,得-x+3=0.解得x=3.∴B(3,0).∴OB=3.
∴△OAB的面积
(3)存在点 M,使△OMC的面积与△OAB的面积相等,理由如下:
∵C(0,3),∴OC=3.∴OB=OC=3.
∵△OMC的面积与△OAB的面积相等,
∴M到y轴的距离等于点A的纵坐标.
∴ 点M 的横坐标为2或-2.
当点 M的横坐标为2时,
将x=2代入y=2x,得y=4,则点M的坐标为(2,4).
当点 M 的横坐标为-2时,
将x=-2代入y=2x,得y=-4,则点M的坐标为( -2,-4).
综上所述,点M的坐标为(2,4)或( -2,-4).
23.解:(1)∵∠B=40°,∠C=60°,∠BAC+∠B+∠C=180°,∴∠BAC=80°.
∵AE是△ABC的高,∴∠AEC=90°.∵∠C=60°,∴∠CAE=90°-60°=30°.
∵AD 是∠BAC的角平分线,
∴∠DAE=∠CAD-∠CAE=10°.
(2)∵∠BAC+∠B+∠C=180°.∴∠BAC=180°-∠B-∠C.
∵AE是△ABC的高,∴∠AEC=90°,∴∠CAE=90°-∠C.
∵AD 是∠BAC的角平分线,
即
(3)∵∠CAE和∠BCF的角平分线交于点G,
∴∠CAE=2∠CAG,∠FCB=2∠FCG.
∵∠CAE=∠FCB-∠AEC,∠CAG=∠FCG-∠G,
∴2∠FCG--∠AEC=2(∠FCG--∠G)=2∠FCG-2∠G,即∠AEC=2∠G.
∵AE是△ABC的高,∴∠AEC=90°.∴∠G=45°.
同课章节目录
