沪科版数学八年级上册 第十四章 全等三角形 知识分类练(含答案)
文档属性
| 名称 | 沪科版数学八年级上册 第十四章 全等三角形 知识分类练(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-07 00:00:00 | ||
图片预览


文档简介
第 十四 章 全等三角形
考点一 全等三角形
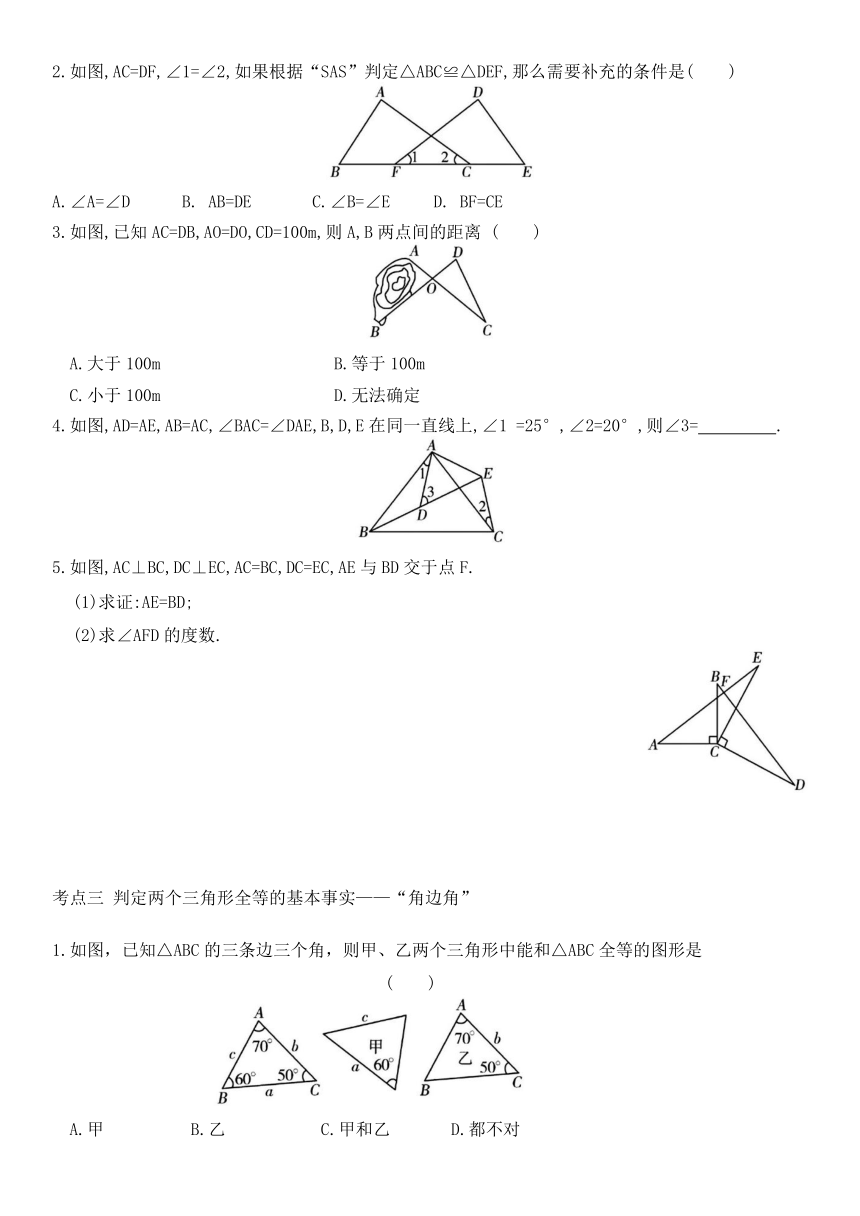
1.在如图所示的图形中,全等图形有 ( )
A.1 对 B.2对 C.3对 D.4对
2.如图,已知△ABE≌△ACD,且∠B =∠C,则下列结论:①∠1 =∠2;②∠BAD=∠CAE;③AD=AE;④DB=EC.其中错误的个数为 ( )
A.0 B.1 C.2 D.3
3.如图,已知△ABC≌△ADC,∠B+∠D=160°,则∠B的度数是 ( )
A.80° B.90° C.100° D.120°
4.如图,已知△ABC≌△ADE,若AB=7,AC=3,则BE的值为 .
5.如图,△ABC≌△ADE,且∠EAB=120°,∠B=30°,∠CAD=10°,∠CFD= °.
6.如图,A,D,E 三点在同一直线上,且△BAD≌△ACE,求证:BD =CE+DE.
考点二 判定两个三角形全等的基本事实——“边角边”
1.在△ABC和△DEF中,下列给出的条件,能用“SAS”判定这两个三角形全等的是( )
A. AB=DE,BC=DF,∠A=∠D
B. AB=BC,DE=EF,∠B=∠E
C. AB=EF,AC=DF,∠A =∠D
D. BC=EF,AC=DF,∠C=∠F
2.如图,AC=DF,∠1=∠2,如果根据“SAS”判定△ABC≌△DEF,那么需要补充的条件是( )
A.∠A=∠D B. AB=DE C.∠B=∠E D. BF=CE
3.如图,已知AC=DB,AO=DO,CD=100m,则A,B两点间的距离 ( )
A.大于100m B.等于100m
C.小于100m D.无法确定
4.如图,AD=AE,AB=AC,∠BAC=∠DAE,B,D,E在同一直线上,∠1 =25°,∠2=20°,则∠3= .
5.如图,AC⊥BC,DC⊥EC,AC=BC,DC=EC,AE与BD交于点F.
(1)求证:AE=BD;
(2)求∠AFD的度数.
考点三 判定两个三角形全等的基本事实——“角边角”
1.如图,已知△ABC的三条边三个角,则甲、乙两个三角形中能和△ABC全等的图形是 ( )
A.甲 B.乙 C.甲和乙 D.都不对
2.如图,已知 ∠ABC=∠DEF,AB=DE,若以“ASA”为依据判定△ABC≌△DEF,还需添加的一个条件为 ( )
A.∠A=∠D
B.∠ACB =∠DFE
C. BC=EF
D. BE=CF
3.在下列条件中,可以判定两个三角形全等的条件是 ( )
A.三个角对应相等
B.一边对应相等且这边上的高也对应相等
C.两角对应相等且这两个角的夹边也对应相等
D.两边对应相等且其中一边的对角也对应相等
4.如图,有一块三角形玻璃裂成两块,现需要配制一块同样大小的玻璃,只需第 块玻璃碎片就可配制.
5.如图,D,C是线段AF上的点,且AB∥DE,BC∥EF,AC=DF.若∠A=60°,∠B=40°, CF=3cm,则
6.如图,AE和BD相交于点C,AB∥ED,AC=EC,求证:BC=DC.
考点四 判定两个三角形全等的基本事实——“边边边”
1.如图,在△ABC中,AB=AC,EB=EC,则由SSS可以判定 ( )
A.△ABD≌△ACD B.△ABE≌△ACE
C.△BDE≌△CDE D.以上都不对
2.如图,AB=AC,根据“SSS”判定△ABO≌△ACO,还应添加条件是 ( )
A. AD=AE B. OD=OE
C. OB=OC D. BD=CE
3.在△ABF和△DCE中,已知AB=9cm,BF=8cm,AF=5cm,DC=9cm,CE=8cm,则当DE=_时,△ABF≌△DCE,判定的依据是
4.如图所示是一个窗户的示意图,将窗扇打开时,通常用风钩AB将窗扇固定,这样做的数学道理是 .
5.如图,在△ABD与△ACE中,已知AB=AC,BD=CE,AD=AE,∠1 =20°,求∠2的度数.
考点五 判定两个三角形全等的基本事实——“角角边”
1.下列条件中,不能判定. 的是 ( )
A. AB=A'B',∠A=∠A',AC=A'C'
B. AB=A'B',∠A=∠A',∠B=∠B'
C. AB=A'B',∠B=∠B',∠C=∠C'
D.∠A=∠A',∠B=∠B',∠C=∠C'
2.如图,∠E=∠F=90°,∠B=∠C,AB=AC,结论:①AE=AF;②CD=DN;③EM=FN;④△ACN≌△ABM.其中正确的有 ( )
A.1个 B.2个 C.3个 D.4个
3.如图,已知∠1=∠2,则不一定能使△ABD≌△ACD的条件是 ( )
A. AB=AC B. BD=CD
C.∠B=∠C D.∠BDA=∠CDA
4.如图, BD与AC相交于点 O,且BO=DO,要利用“AAS”判定△AOB≌△COD,应添加条件 .
5.如图,B,C,E三点在同一条直线上,AC∥DE,AC=CE,∠ACD=∠B.求证:△ABC≌△CDE.
E
考点六 判定两个三角形全等的基本事实——“斜边、直角边”
1.下列说法中,正确的个数是 ( )
①斜边和一条直角边对应相等的两个直角三角形全等;
②有两边和它们的夹角对应相等的两个直角三角形全等;
③一锐角和斜边对应相等的两个直角三角形全等;
④两个锐角对应相等的两个直角三角形全等.
A.1个 B.2个 C.3个 D.4个
2.如图,点P是∠BAC内一点,且到AB,AC的距离PE,PF 相等,则△PEA≌△PFA的依据是( )
A. HL B. AAS C. SSS D. SAS
3.如图,在△ABC和△ABD中,∠C=∠D=90°,若利用“HL”证明△ABC≌△ABD,则需要加条件 ( )
A.∠CAB =∠DAB B.∠ABC=∠ABD
C. AB=AB D. AC=AD 或BC=BD
4.如图,在△ABC中,∠C=90°,点 D 是BC边上的一点,DE⊥AB,垂足为E,若CD=ED,则Rt△CDA≌ .
5.如图,小明和小芳以相同的速度分别同时从A,B出发,小明沿AC行走,小芳沿 BD行走,并同时到达C,D,若CB⊥AB,DA⊥AB,则CB DA.(填“>”“<”或“=”)
6.在Rt△ABC中,∠C=90°,AC=15cm,BC=8cm,AX⊥AC于A,P,Q两点分别在边AC和射线AX上移动,当PQ=AB,AP= cm时,△ABC和△APQ 全等.
7.如图,AD,BC相交于点O,AD=BC,∠C=∠D=90°.
(1)求证:△ACB≌△BDA;
(2)若∠ABC=35°,求∠CAD.
第十四 章 全等三角形
考点一 全等三角形
1. B 2. A 3. A 4.4 5.95
6.证明:∵△BAD≌△ACE,∴BD=AE,AD=CE.∵AE=AD+DE,∴BD=CE+DE.
考点二 判定两个三角形全等的基本事实——“边角边”
1. D 2. D 3. B 4.45°
5.证明:(1)∵AC⊥BC,DC⊥EC,∴∠ACB=∠ECD=90°.
∴∠ACB+∠BCE=∠ECD+∠BCE.∴∠ACE=∠BCD.
在△ACE和△BCD 中,
(2)设BD 与CE的交点为 G.∵△ACE≌△BCD,∴∠E =∠D.
∵∠EFG+∠FGE+∠E=180°,∠GCD+∠CGD+∠D=180°,且∠BGE=∠CGD,∴∠EFG=∠GCD=90°.∴∠AFD=90°.
考点三 判定两个三角形全等的基本事实——“角边角”
1. B 2. A 3. C 4.② 5.80° 3cm
6.证明:∵AB∥ED,∴∠A=∠E.在△ABC和△EDC 中,
∴△ABC≌△EDC(ASA)∴BC=DC.
考点四 判定两个三角形全等的基本事实——“边边边”
1. B 2. C 3.5cm SSS 4.三角形的稳定性
5.解:在△ABD和△ACE中,
∴∠BAD-∠BAC=∠CAE--∠BAC,即
考点五 判定两个三角形全等的基本事实——“角角边”
1. D 2. C 3. B 4.∠A=∠C
5.证明:∵AC∥DE,∴∠ACD=∠D,∠ACB=∠E.
又∵∠B=∠ACD,∴∠B=∠D.
在△ABC 和△CDE 中,
考点六 判定两个三角形全等的基本事实——“斜边、直角边”
1. C 2. A 3. D 4. Rt△EDA 5. = 6.8或15
7.(1)证明:在 Rt△ACB和Rt△BDA 中,{BC=AD,∴Rt△ACB≌△Rt△BDA(HL).
(2)解:∵Rt△ACB≌Rt△BDA,∠ABC=35°,∴∠ABC=∠DAB=35°.
在△ABC中,∠CAB=90°-∠ABC=90°-35°=55°.
∴∠CAD=∠CAB-∠DAB=55°-35°=20°.
考点一 全等三角形
1.在如图所示的图形中,全等图形有 ( )
A.1 对 B.2对 C.3对 D.4对
2.如图,已知△ABE≌△ACD,且∠B =∠C,则下列结论:①∠1 =∠2;②∠BAD=∠CAE;③AD=AE;④DB=EC.其中错误的个数为 ( )
A.0 B.1 C.2 D.3
3.如图,已知△ABC≌△ADC,∠B+∠D=160°,则∠B的度数是 ( )
A.80° B.90° C.100° D.120°
4.如图,已知△ABC≌△ADE,若AB=7,AC=3,则BE的值为 .
5.如图,△ABC≌△ADE,且∠EAB=120°,∠B=30°,∠CAD=10°,∠CFD= °.
6.如图,A,D,E 三点在同一直线上,且△BAD≌△ACE,求证:BD =CE+DE.
考点二 判定两个三角形全等的基本事实——“边角边”
1.在△ABC和△DEF中,下列给出的条件,能用“SAS”判定这两个三角形全等的是( )
A. AB=DE,BC=DF,∠A=∠D
B. AB=BC,DE=EF,∠B=∠E
C. AB=EF,AC=DF,∠A =∠D
D. BC=EF,AC=DF,∠C=∠F
2.如图,AC=DF,∠1=∠2,如果根据“SAS”判定△ABC≌△DEF,那么需要补充的条件是( )
A.∠A=∠D B. AB=DE C.∠B=∠E D. BF=CE
3.如图,已知AC=DB,AO=DO,CD=100m,则A,B两点间的距离 ( )
A.大于100m B.等于100m
C.小于100m D.无法确定
4.如图,AD=AE,AB=AC,∠BAC=∠DAE,B,D,E在同一直线上,∠1 =25°,∠2=20°,则∠3= .
5.如图,AC⊥BC,DC⊥EC,AC=BC,DC=EC,AE与BD交于点F.
(1)求证:AE=BD;
(2)求∠AFD的度数.
考点三 判定两个三角形全等的基本事实——“角边角”
1.如图,已知△ABC的三条边三个角,则甲、乙两个三角形中能和△ABC全等的图形是 ( )
A.甲 B.乙 C.甲和乙 D.都不对
2.如图,已知 ∠ABC=∠DEF,AB=DE,若以“ASA”为依据判定△ABC≌△DEF,还需添加的一个条件为 ( )
A.∠A=∠D
B.∠ACB =∠DFE
C. BC=EF
D. BE=CF
3.在下列条件中,可以判定两个三角形全等的条件是 ( )
A.三个角对应相等
B.一边对应相等且这边上的高也对应相等
C.两角对应相等且这两个角的夹边也对应相等
D.两边对应相等且其中一边的对角也对应相等
4.如图,有一块三角形玻璃裂成两块,现需要配制一块同样大小的玻璃,只需第 块玻璃碎片就可配制.
5.如图,D,C是线段AF上的点,且AB∥DE,BC∥EF,AC=DF.若∠A=60°,∠B=40°, CF=3cm,则
6.如图,AE和BD相交于点C,AB∥ED,AC=EC,求证:BC=DC.
考点四 判定两个三角形全等的基本事实——“边边边”
1.如图,在△ABC中,AB=AC,EB=EC,则由SSS可以判定 ( )
A.△ABD≌△ACD B.△ABE≌△ACE
C.△BDE≌△CDE D.以上都不对
2.如图,AB=AC,根据“SSS”判定△ABO≌△ACO,还应添加条件是 ( )
A. AD=AE B. OD=OE
C. OB=OC D. BD=CE
3.在△ABF和△DCE中,已知AB=9cm,BF=8cm,AF=5cm,DC=9cm,CE=8cm,则当DE=_时,△ABF≌△DCE,判定的依据是
4.如图所示是一个窗户的示意图,将窗扇打开时,通常用风钩AB将窗扇固定,这样做的数学道理是 .
5.如图,在△ABD与△ACE中,已知AB=AC,BD=CE,AD=AE,∠1 =20°,求∠2的度数.
考点五 判定两个三角形全等的基本事实——“角角边”
1.下列条件中,不能判定. 的是 ( )
A. AB=A'B',∠A=∠A',AC=A'C'
B. AB=A'B',∠A=∠A',∠B=∠B'
C. AB=A'B',∠B=∠B',∠C=∠C'
D.∠A=∠A',∠B=∠B',∠C=∠C'
2.如图,∠E=∠F=90°,∠B=∠C,AB=AC,结论:①AE=AF;②CD=DN;③EM=FN;④△ACN≌△ABM.其中正确的有 ( )
A.1个 B.2个 C.3个 D.4个
3.如图,已知∠1=∠2,则不一定能使△ABD≌△ACD的条件是 ( )
A. AB=AC B. BD=CD
C.∠B=∠C D.∠BDA=∠CDA
4.如图, BD与AC相交于点 O,且BO=DO,要利用“AAS”判定△AOB≌△COD,应添加条件 .
5.如图,B,C,E三点在同一条直线上,AC∥DE,AC=CE,∠ACD=∠B.求证:△ABC≌△CDE.
E
考点六 判定两个三角形全等的基本事实——“斜边、直角边”
1.下列说法中,正确的个数是 ( )
①斜边和一条直角边对应相等的两个直角三角形全等;
②有两边和它们的夹角对应相等的两个直角三角形全等;
③一锐角和斜边对应相等的两个直角三角形全等;
④两个锐角对应相等的两个直角三角形全等.
A.1个 B.2个 C.3个 D.4个
2.如图,点P是∠BAC内一点,且到AB,AC的距离PE,PF 相等,则△PEA≌△PFA的依据是( )
A. HL B. AAS C. SSS D. SAS
3.如图,在△ABC和△ABD中,∠C=∠D=90°,若利用“HL”证明△ABC≌△ABD,则需要加条件 ( )
A.∠CAB =∠DAB B.∠ABC=∠ABD
C. AB=AB D. AC=AD 或BC=BD
4.如图,在△ABC中,∠C=90°,点 D 是BC边上的一点,DE⊥AB,垂足为E,若CD=ED,则Rt△CDA≌ .
5.如图,小明和小芳以相同的速度分别同时从A,B出发,小明沿AC行走,小芳沿 BD行走,并同时到达C,D,若CB⊥AB,DA⊥AB,则CB DA.(填“>”“<”或“=”)
6.在Rt△ABC中,∠C=90°,AC=15cm,BC=8cm,AX⊥AC于A,P,Q两点分别在边AC和射线AX上移动,当PQ=AB,AP= cm时,△ABC和△APQ 全等.
7.如图,AD,BC相交于点O,AD=BC,∠C=∠D=90°.
(1)求证:△ACB≌△BDA;
(2)若∠ABC=35°,求∠CAD.
第十四 章 全等三角形
考点一 全等三角形
1. B 2. A 3. A 4.4 5.95
6.证明:∵△BAD≌△ACE,∴BD=AE,AD=CE.∵AE=AD+DE,∴BD=CE+DE.
考点二 判定两个三角形全等的基本事实——“边角边”
1. D 2. D 3. B 4.45°
5.证明:(1)∵AC⊥BC,DC⊥EC,∴∠ACB=∠ECD=90°.
∴∠ACB+∠BCE=∠ECD+∠BCE.∴∠ACE=∠BCD.
在△ACE和△BCD 中,
(2)设BD 与CE的交点为 G.∵△ACE≌△BCD,∴∠E =∠D.
∵∠EFG+∠FGE+∠E=180°,∠GCD+∠CGD+∠D=180°,且∠BGE=∠CGD,∴∠EFG=∠GCD=90°.∴∠AFD=90°.
考点三 判定两个三角形全等的基本事实——“角边角”
1. B 2. A 3. C 4.② 5.80° 3cm
6.证明:∵AB∥ED,∴∠A=∠E.在△ABC和△EDC 中,
∴△ABC≌△EDC(ASA)∴BC=DC.
考点四 判定两个三角形全等的基本事实——“边边边”
1. B 2. C 3.5cm SSS 4.三角形的稳定性
5.解:在△ABD和△ACE中,
∴∠BAD-∠BAC=∠CAE--∠BAC,即
考点五 判定两个三角形全等的基本事实——“角角边”
1. D 2. C 3. B 4.∠A=∠C
5.证明:∵AC∥DE,∴∠ACD=∠D,∠ACB=∠E.
又∵∠B=∠ACD,∴∠B=∠D.
在△ABC 和△CDE 中,
考点六 判定两个三角形全等的基本事实——“斜边、直角边”
1. C 2. A 3. D 4. Rt△EDA 5. = 6.8或15
7.(1)证明:在 Rt△ACB和Rt△BDA 中,{BC=AD,∴Rt△ACB≌△Rt△BDA(HL).
(2)解:∵Rt△ACB≌Rt△BDA,∠ABC=35°,∴∠ABC=∠DAB=35°.
在△ABC中,∠CAB=90°-∠ABC=90°-35°=55°.
∴∠CAD=∠CAB-∠DAB=55°-35°=20°.
