沪科版数学八年级上册第14章 全等三角形(含答案)
文档属性
| 名称 | 沪科版数学八年级上册第14章 全等三角形(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 980.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-07 00:00:00 | ||
图片预览


文档简介
第 14 章 全等三角形
(时间:120分钟满分:150分)
题 号 一 二 三 四 五 六 七 八 总分
得 分
一、选择题(本大题共10 小题,每小题4分,满分40 分)
1.下列选项中表示两个全等图形的是 ( )
A.形状相同的两个图形 B.能够完全重合的两个图形
C.面积相等的两个图形 D.周长相等的两个图形
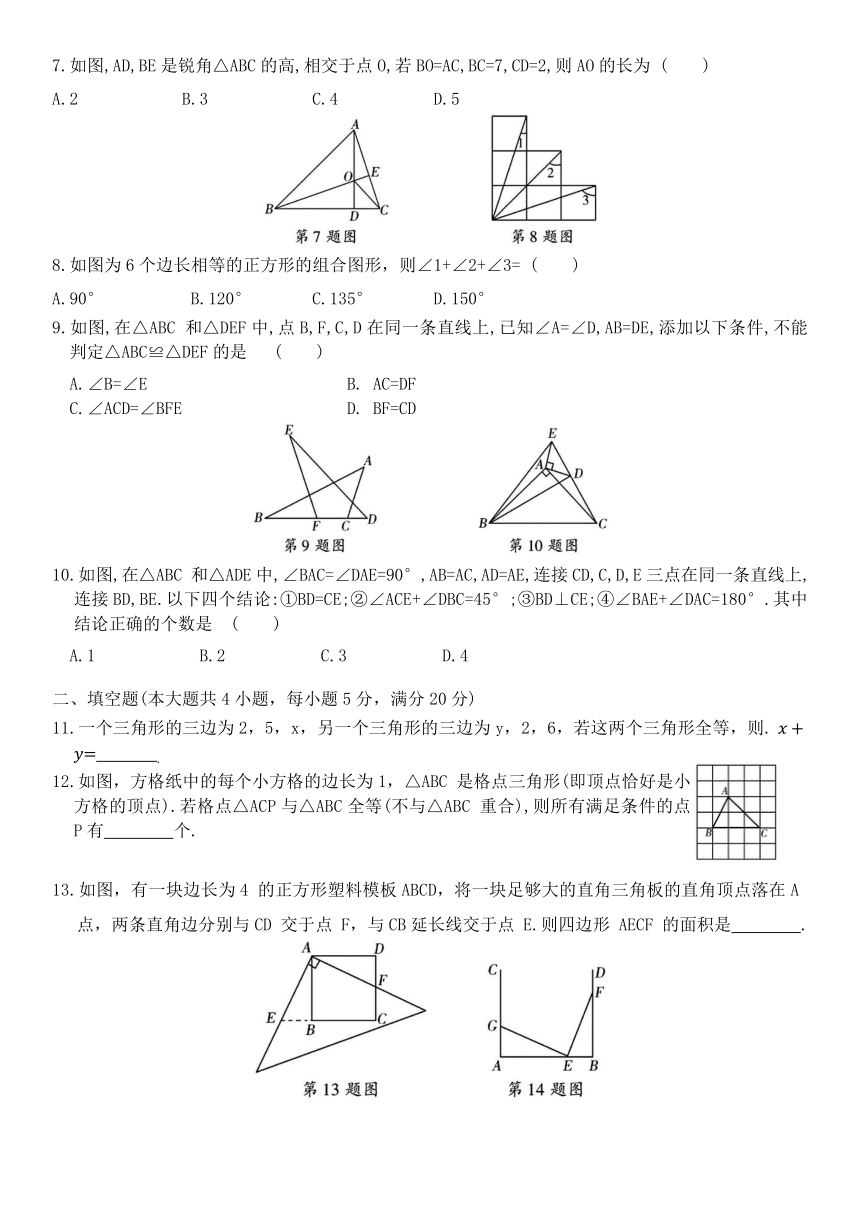
2.王师傅用4根木条钉成一个四边形木架,如图.要使这个木架不变形,他至少还要再钉上几根木条 ( )
A.0根 B.1 根 C.2 根 D.3根
3.如图是用直尺和圆规作一个角等于已知角的示意图,则说明. ∠AOB的依据是 ( )
A. SSS B. SAS C. ASA D. AAS
4.要测量池塘的宽度AB,画出如图所示的两个三角形,下面所测出的条件中不能得出CD=AB 的是 ( )
A. OA=OD,OB=OC
B.∠B=∠C,OB=OC
C.∠C=∠B,∠A=∠D
D.∠B=∠C,OA=OD
5.下列各图中a,b,c为三角形的边长,则甲、乙、丙三个三角形和左侧△ABC全等的是( )
A.甲和乙 B.乙和丙 C.甲和丙 D.只有丙
6.根据下列条件,能画出唯一△ABC的是 ( )
A.∠A=60°,∠B=45°,AB=4
B. AB=4,BC=3,∠A=30°
C. AB=3,BC=4,AC=8
D.∠C=90°,AB=6
7.如图,AD,BE是锐角△ABC的高,相交于点O,若BO=AC,BC=7,CD=2,则AO的长为 ( )
A.2 B.3 C.4 D.5
8.如图为6个边长相等的正方形的组合图形,则∠1+∠2+∠3= ( )
A.90° B.120° C.135° D.150°
9.如图,在△ABC 和△DEF中,点B,F,C,D在同一条直线上,已知∠A=∠D,AB=DE,添加以下条件,不能判定△ABC≌△DEF的是 ( )
A.∠B=∠E B. AC=DF
C.∠ACD=∠BFE D. BF=CD
10.如图,在△ABC 和△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,连接CD,C,D,E三点在同一条直线上,连接BD,BE.以下四个结论:①BD=CE;②∠ACE+∠DBC=45°;③BD⊥CE;④∠BAE+∠DAC=180°.其中结论正确的个数是 ( )
A.1 B.2 C.3 D.4
二、填空题(本大题共4小题,每小题5分,满分20分)
11.一个三角形的三边为2,5,x,另一个三角形的三边为y,2,6,若这两个三角形全等,则.
12.如图,方格纸中的每个小方格的边长为1,△ABC 是格点三角形(即顶点恰好是小方格的顶点).若格点△ACP与△ABC全等(不与△ABC 重合),则所有满足条件的点P有 个.
13.如图,有一块边长为4 的正方形塑料模板ABCD,将一块足够大的直角三角板的直角顶点落在A 点,两条直角边分别与CD 交于点 F,与CB延长线交于点 E.则四边形 AECF 的面积是 .
14.如图, E,F 分别为线段 AB 和射线 BD 上的一点,若点 E 从点 B 出发向点 A 运动,同时点 F 从点 B 出发向点 D 运动,二者速度之比为3:7,运动到某时刻同时停止,在射线AC上取一点 G,使 与 全等,则AG的长为 .
三、(本大题共2 小题,每小题8分,满分16 分)
15.如图,AB,CD相交于点 O, ,点 E 在 AC 上,EO 的延长线交 BD 于点 F.求证:O 是EF 的中点.
16.如图,已知△EFG≌△NMH,∠F与∠M是对应角.
(1)写出所有相等的线段与相等的角;
(2)若 ,求MN和 HG的长度.
四、(本大题共2 小题,每小题8分,满分16 分)
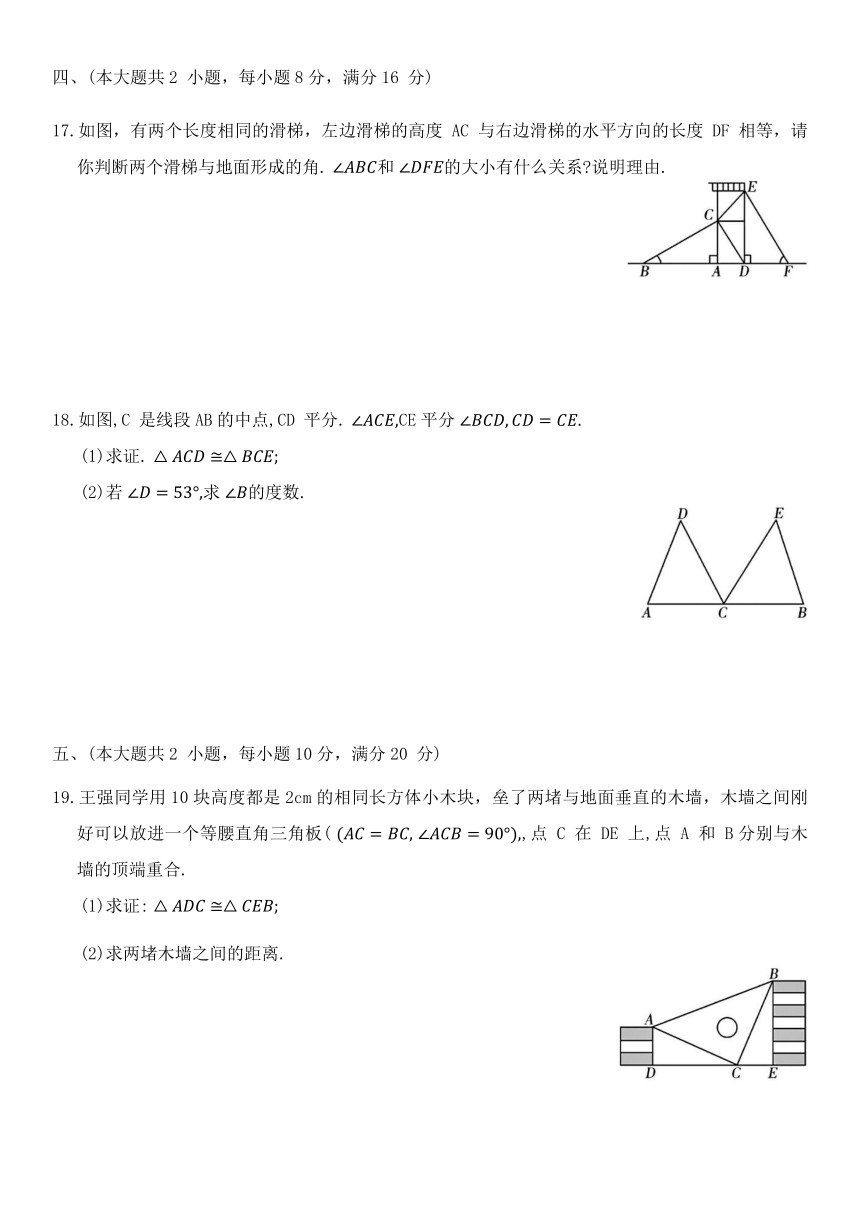
17.如图,有两个长度相同的滑梯,左边滑梯的高度 AC 与右边滑梯的水平方向的长度 DF 相等,请你判断两个滑梯与地面形成的角. 和 的大小有什么关系 说明理由.
18.如图,C 是线段AB的中点,CD 平分. CE平分
(1)求证.
(2)若 求 的度数.
五、(本大题共2 小题,每小题10分,满分20 分)
19.王强同学用10块高度都是2cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板( ,点 C 在 DE 上,点 A 和 B分别与木墙的顶端重合.
(1)求证:
(2)求两堵木墙之间的距离.
20.如图,在线段BC上有两点 E,F,在线段BC 的异侧有两点A,D,且满足 连接AF.
与 相等吗 请说明理由;
(2)若 ,当AF 平分. 时,求 的度数.
六、(本题满分12 分)
21.如图,点A,B,C,D在同一条直线上,点 E,F 是直线AD 上方的点,连接AE,CE,BF,DF,若.
(1)判断直线 CE 与 DF 是否平行,并说明理由;
(2)求 CD的长;
(3)若 求 的度数.
七、(本题满分12 分)
22.如图,∠ ,垂足为点 F.
(1)求证:
(2)求 的度数;
(3)求证:
八、(本题满分14分)
23.在 中, , D 为 AB 边的中点,动点P 在 BC 边上从点 B 向点 C 以: 的速度运动,同时点 Q 在线段 CA上从点 C 向点 A 运动.
(1)若点P,Q 的速度相等,经过1 s后, 与 是否全等 为什么
(2)若点 Q 的速度与点 P 的速度不相等,当点 Q 的速度为多少时,能使
(3)求经过多少秒后, 与 全等
第14章 全等三角形
1. B 2. B 3. A 4. C 5. B 6. A 7. B 8. C 9. D 10. D
11.11 12.3 13.16 14.18或70
15.证明:∵△AOC≌△BOD,∴∠A=∠B,OA=OB.
在△AEO 和△BFO中,
∴△AEO≌△BFO(ASA).∴OE=OF.∴O是EF的中点.
16.解:(1)EF =NM,EG=NH,FG=MH,FH=MG,∠F =∠M,∠E =∠N,∠EGF =∠NHM,∠FHN=∠MGE.
(2)∵△EFG≌△NMH,EF=2.1cm,FH=1.1cm,HM=3.3cm,
∴MN=EF=2.1 cm,GF=HM=3.3cm.
∴HG=GF-FH=3.3-1.1=2.2(cm).
17.解:∠ABC与∠DFE互余,理由如下:
根据题意,得BC=EF,AC=DF.∠BAC=∠EDF=90°.
在Rt△ABC和Rt△DEF 中,{AC=DF;∴Rt△ABC≌Rt△DEF(HL),∴∠B=∠DEF.
又∵∠DEF+∠DFE=90°,∴∠B+∠DFE=90°,即∠B与∠DFE互余.
18.(1)证明:∵CD平分∠ACE,∴∠ACD=∠DCE.
∵CE平分∠BCD,∴∠DCE=∠BCE.∴∠ACD=∠BCE.
∵ C 是线段AB的中点,∴AC =BC.
在△ACD与△BCE中,
(2)解:由(1)可知,.
∵△ACD≌△BCE,∴∠E=∠D=53°.∴∠B=180°-60°-53°=67°.
19.(1)证明:根据题意,得AC=BC,∠ACB=90°,AD⊥DE,BE⊥DE,∴∠ADC=∠CEB=90°.
∴∠ACD+∠BCE=90°,∠ACD+∠CAD=90°.∴∠BCE=∠CAD.
在△ADC和△CEB中,
(2)解:根据题意,得AD=2×3=6(cm),EB=7×2=14(cm).
∵△ADC≌△CEB,∴CE=AD=6cm,DC=EB=14 cm.
∴DE=DC+CE=20(cm).
答:两堵木墙之间的距离为20cm.
20.解:(1)∠B=∠C.理由如下:
∵BF=CE,∴BF+EF=CE+EF,即BE=CF.
在△AEB和△DFC 中,
(2)∵△AEB≌△DFC,∴∠AEB=∠DFC=20°.
∴∠EAB=180°-∠B-∠AEB=120°.
∵ AF平分
21.解:(1)CE∥DF.理由如下:
∵△ACE≌△FDB,∴∠ACE=∠D.∴CE∥DF.
(2)∵△ACE≌△FDB,∴AC=FD=3.
∵AD=8,∴CD=AD-AC=8-3=5.
(3)∵△ACE≌△FDB,∴∠DBF=∠E=26°.
∵CE∥DF,∴∠1 =∠F=53°.
∴∠ACE=180°-26°-53°=101°.
22.(1)证明:∵∠BAD=∠CAE=90°,
∴∠BAC+∠CAD=90°,∠CAD+∠DAE=90°.∴∠BAC=∠DAE.
在△ABC 和△ADE中,
(2)解:∵∠CAE=90°,AC=AE,∴△ACE是等腰直角三角形.∴∠E=45°.
由(1)知△ABC≌△ADE,∴∠BCA=∠E=45°.
∵AF⊥BC,∴∠CFA=90°.∴∠CAF=45°.
∴∠FAE=∠FAC+∠CAE=45°+90°=135°.
(3)证明:延长BF到G,使得 FG=FB.
∵AF⊥BG,∴∠AFG=∠AFB=90°.
在△AFB 和△AFG中,
∴△AFB≌△AFG(SAS).∴AB=AG,∠ABF=∠G.
∵△ABC≌△ADE,∴AB=AD,∠CBA=∠EDA,CB=ED.
∴AG=AD,∠ABF=∠CDA.∴∠G=∠CDA.
∵∠GCA=∠DCA=45°,
在△CGA 和△CDA 中,
∵CG=CB+BF+FG=CB+2BF=DE+2BF,∴CD=2BF+DE.
23.解:(1)△BPD≌△CQP.理由如下:
根据题意,得BP=CQ=3cm,CP=BC-BP=5cm.
∵ D 为AB 中点,
在△BPD和△CQP中,
(2)设点Q的运动速度为a cm/s,则经过ts后,BD=5cm,BP=3tcm,CP=(8-3t) cm,CQ=at cm.
∵点Q的运动速度与点P的运动速度不相等,∴BP≠CQ.
要使△BPD≌△CPQ,则需BP=CP,BD=CQ.∴3t=8-3t, at=5.
∴点 P、点 Q 的运动时间 点Q的速度是
(3)设经过xs后,△BPD与△CPQ全等,分两种情况:
①当△BPD≌△CPQ时,则 则
②当△BPD≌△CQP时,BD=CP=5cm,则BP=BC-PC=3cm,则 综上所述,经过- 或1s后,△BPD与△CPQ 全等.
(时间:120分钟满分:150分)
题 号 一 二 三 四 五 六 七 八 总分
得 分
一、选择题(本大题共10 小题,每小题4分,满分40 分)
1.下列选项中表示两个全等图形的是 ( )
A.形状相同的两个图形 B.能够完全重合的两个图形
C.面积相等的两个图形 D.周长相等的两个图形
2.王师傅用4根木条钉成一个四边形木架,如图.要使这个木架不变形,他至少还要再钉上几根木条 ( )
A.0根 B.1 根 C.2 根 D.3根
3.如图是用直尺和圆规作一个角等于已知角的示意图,则说明. ∠AOB的依据是 ( )
A. SSS B. SAS C. ASA D. AAS
4.要测量池塘的宽度AB,画出如图所示的两个三角形,下面所测出的条件中不能得出CD=AB 的是 ( )
A. OA=OD,OB=OC
B.∠B=∠C,OB=OC
C.∠C=∠B,∠A=∠D
D.∠B=∠C,OA=OD
5.下列各图中a,b,c为三角形的边长,则甲、乙、丙三个三角形和左侧△ABC全等的是( )
A.甲和乙 B.乙和丙 C.甲和丙 D.只有丙
6.根据下列条件,能画出唯一△ABC的是 ( )
A.∠A=60°,∠B=45°,AB=4
B. AB=4,BC=3,∠A=30°
C. AB=3,BC=4,AC=8
D.∠C=90°,AB=6
7.如图,AD,BE是锐角△ABC的高,相交于点O,若BO=AC,BC=7,CD=2,则AO的长为 ( )
A.2 B.3 C.4 D.5
8.如图为6个边长相等的正方形的组合图形,则∠1+∠2+∠3= ( )
A.90° B.120° C.135° D.150°
9.如图,在△ABC 和△DEF中,点B,F,C,D在同一条直线上,已知∠A=∠D,AB=DE,添加以下条件,不能判定△ABC≌△DEF的是 ( )
A.∠B=∠E B. AC=DF
C.∠ACD=∠BFE D. BF=CD
10.如图,在△ABC 和△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,连接CD,C,D,E三点在同一条直线上,连接BD,BE.以下四个结论:①BD=CE;②∠ACE+∠DBC=45°;③BD⊥CE;④∠BAE+∠DAC=180°.其中结论正确的个数是 ( )
A.1 B.2 C.3 D.4
二、填空题(本大题共4小题,每小题5分,满分20分)
11.一个三角形的三边为2,5,x,另一个三角形的三边为y,2,6,若这两个三角形全等,则.
12.如图,方格纸中的每个小方格的边长为1,△ABC 是格点三角形(即顶点恰好是小方格的顶点).若格点△ACP与△ABC全等(不与△ABC 重合),则所有满足条件的点P有 个.
13.如图,有一块边长为4 的正方形塑料模板ABCD,将一块足够大的直角三角板的直角顶点落在A 点,两条直角边分别与CD 交于点 F,与CB延长线交于点 E.则四边形 AECF 的面积是 .
14.如图, E,F 分别为线段 AB 和射线 BD 上的一点,若点 E 从点 B 出发向点 A 运动,同时点 F 从点 B 出发向点 D 运动,二者速度之比为3:7,运动到某时刻同时停止,在射线AC上取一点 G,使 与 全等,则AG的长为 .
三、(本大题共2 小题,每小题8分,满分16 分)
15.如图,AB,CD相交于点 O, ,点 E 在 AC 上,EO 的延长线交 BD 于点 F.求证:O 是EF 的中点.
16.如图,已知△EFG≌△NMH,∠F与∠M是对应角.
(1)写出所有相等的线段与相等的角;
(2)若 ,求MN和 HG的长度.
四、(本大题共2 小题,每小题8分,满分16 分)
17.如图,有两个长度相同的滑梯,左边滑梯的高度 AC 与右边滑梯的水平方向的长度 DF 相等,请你判断两个滑梯与地面形成的角. 和 的大小有什么关系 说明理由.
18.如图,C 是线段AB的中点,CD 平分. CE平分
(1)求证.
(2)若 求 的度数.
五、(本大题共2 小题,每小题10分,满分20 分)
19.王强同学用10块高度都是2cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板( ,点 C 在 DE 上,点 A 和 B分别与木墙的顶端重合.
(1)求证:
(2)求两堵木墙之间的距离.
20.如图,在线段BC上有两点 E,F,在线段BC 的异侧有两点A,D,且满足 连接AF.
与 相等吗 请说明理由;
(2)若 ,当AF 平分. 时,求 的度数.
六、(本题满分12 分)
21.如图,点A,B,C,D在同一条直线上,点 E,F 是直线AD 上方的点,连接AE,CE,BF,DF,若.
(1)判断直线 CE 与 DF 是否平行,并说明理由;
(2)求 CD的长;
(3)若 求 的度数.
七、(本题满分12 分)
22.如图,∠ ,垂足为点 F.
(1)求证:
(2)求 的度数;
(3)求证:
八、(本题满分14分)
23.在 中, , D 为 AB 边的中点,动点P 在 BC 边上从点 B 向点 C 以: 的速度运动,同时点 Q 在线段 CA上从点 C 向点 A 运动.
(1)若点P,Q 的速度相等,经过1 s后, 与 是否全等 为什么
(2)若点 Q 的速度与点 P 的速度不相等,当点 Q 的速度为多少时,能使
(3)求经过多少秒后, 与 全等
第14章 全等三角形
1. B 2. B 3. A 4. C 5. B 6. A 7. B 8. C 9. D 10. D
11.11 12.3 13.16 14.18或70
15.证明:∵△AOC≌△BOD,∴∠A=∠B,OA=OB.
在△AEO 和△BFO中,
∴△AEO≌△BFO(ASA).∴OE=OF.∴O是EF的中点.
16.解:(1)EF =NM,EG=NH,FG=MH,FH=MG,∠F =∠M,∠E =∠N,∠EGF =∠NHM,∠FHN=∠MGE.
(2)∵△EFG≌△NMH,EF=2.1cm,FH=1.1cm,HM=3.3cm,
∴MN=EF=2.1 cm,GF=HM=3.3cm.
∴HG=GF-FH=3.3-1.1=2.2(cm).
17.解:∠ABC与∠DFE互余,理由如下:
根据题意,得BC=EF,AC=DF.∠BAC=∠EDF=90°.
在Rt△ABC和Rt△DEF 中,{AC=DF;∴Rt△ABC≌Rt△DEF(HL),∴∠B=∠DEF.
又∵∠DEF+∠DFE=90°,∴∠B+∠DFE=90°,即∠B与∠DFE互余.
18.(1)证明:∵CD平分∠ACE,∴∠ACD=∠DCE.
∵CE平分∠BCD,∴∠DCE=∠BCE.∴∠ACD=∠BCE.
∵ C 是线段AB的中点,∴AC =BC.
在△ACD与△BCE中,
(2)解:由(1)可知,.
∵△ACD≌△BCE,∴∠E=∠D=53°.∴∠B=180°-60°-53°=67°.
19.(1)证明:根据题意,得AC=BC,∠ACB=90°,AD⊥DE,BE⊥DE,∴∠ADC=∠CEB=90°.
∴∠ACD+∠BCE=90°,∠ACD+∠CAD=90°.∴∠BCE=∠CAD.
在△ADC和△CEB中,
(2)解:根据题意,得AD=2×3=6(cm),EB=7×2=14(cm).
∵△ADC≌△CEB,∴CE=AD=6cm,DC=EB=14 cm.
∴DE=DC+CE=20(cm).
答:两堵木墙之间的距离为20cm.
20.解:(1)∠B=∠C.理由如下:
∵BF=CE,∴BF+EF=CE+EF,即BE=CF.
在△AEB和△DFC 中,
(2)∵△AEB≌△DFC,∴∠AEB=∠DFC=20°.
∴∠EAB=180°-∠B-∠AEB=120°.
∵ AF平分
21.解:(1)CE∥DF.理由如下:
∵△ACE≌△FDB,∴∠ACE=∠D.∴CE∥DF.
(2)∵△ACE≌△FDB,∴AC=FD=3.
∵AD=8,∴CD=AD-AC=8-3=5.
(3)∵△ACE≌△FDB,∴∠DBF=∠E=26°.
∵CE∥DF,∴∠1 =∠F=53°.
∴∠ACE=180°-26°-53°=101°.
22.(1)证明:∵∠BAD=∠CAE=90°,
∴∠BAC+∠CAD=90°,∠CAD+∠DAE=90°.∴∠BAC=∠DAE.
在△ABC 和△ADE中,
(2)解:∵∠CAE=90°,AC=AE,∴△ACE是等腰直角三角形.∴∠E=45°.
由(1)知△ABC≌△ADE,∴∠BCA=∠E=45°.
∵AF⊥BC,∴∠CFA=90°.∴∠CAF=45°.
∴∠FAE=∠FAC+∠CAE=45°+90°=135°.
(3)证明:延长BF到G,使得 FG=FB.
∵AF⊥BG,∴∠AFG=∠AFB=90°.
在△AFB 和△AFG中,
∴△AFB≌△AFG(SAS).∴AB=AG,∠ABF=∠G.
∵△ABC≌△ADE,∴AB=AD,∠CBA=∠EDA,CB=ED.
∴AG=AD,∠ABF=∠CDA.∴∠G=∠CDA.
∵∠GCA=∠DCA=45°,
在△CGA 和△CDA 中,
∵CG=CB+BF+FG=CB+2BF=DE+2BF,∴CD=2BF+DE.
23.解:(1)△BPD≌△CQP.理由如下:
根据题意,得BP=CQ=3cm,CP=BC-BP=5cm.
∵ D 为AB 中点,
在△BPD和△CQP中,
(2)设点Q的运动速度为a cm/s,则经过ts后,BD=5cm,BP=3tcm,CP=(8-3t) cm,CQ=at cm.
∵点Q的运动速度与点P的运动速度不相等,∴BP≠CQ.
要使△BPD≌△CPQ,则需BP=CP,BD=CQ.∴3t=8-3t, at=5.
∴点 P、点 Q 的运动时间 点Q的速度是
(3)设经过xs后,△BPD与△CPQ全等,分两种情况:
①当△BPD≌△CPQ时,则 则
②当△BPD≌△CQP时,BD=CP=5cm,则BP=BC-PC=3cm,则 综上所述,经过- 或1s后,△BPD与△CPQ 全等.
