沪科版数学八年级上册 月考检测卷(二)(含答案)
文档属性
| 名称 | 沪科版数学八年级上册 月考检测卷(二)(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-07 00:00:00 | ||
图片预览



文档简介
月考检测卷(二)
(时间:120分钟满分:150分)
题 号 一 二 三 四 五 六 七 八 总 分
得 分
一、选择题(本大题共10 小题,每小题4分,满分40 分)
1.确定平面直角坐标系内点的位置是 ( )
A.一个实数 B.一个整数 C.一对实数 D.有序实数对
2.下列长度的三条线段,能构成三角形的是 ( )
A.1,2,3 B.3,4,5 C.5,12,17 D.6,8,20
3.下列函数①y=-5x;②y=-2x+1;③y= ;④y= x+6;⑤y=x -1中,是一次函数的有( )
A.1个 B.2个 C.3个 D.4个
4.下列命题为真命题的是 ( )
A.若|x|=|y|,则x=y
B.若a>b,则 ac>bc
C.任何一个角都比它的补角小
D.三角形的三条中线相交于一点
5.如图,将∠A,∠1,∠2的大小排列正确的是 ( )
A.∠1 >∠2 >∠A B.∠1>∠A>∠2
C.∠A>∠1 >∠2 D.∠2>∠1 >∠A
6.一个三角形的两边长为6和8,第三边长为偶数,则第三边长的最大值为( )
A.5 B.9 C.12 D.14
7.如图,D是AB上一点,DF交AC于点E,DE=FE,FC∥AB,若AB=4,CF=3,则BD的长是( )
A.0.5 B.1 C.1.5 D.2
8.若直线y=kx+b经过点(3,0),( 则kx+b >0 的解集是( )
B. x<3
C. x>3
9.如图,∠ACB=∠DFE,BC=EF,如果要使得△ABC≌△DEF,则还须补充的一个条件可以是( )
A.∠ABC =∠DEF B.∠ACE=∠DFB
C. BF=EC D. AB =DE
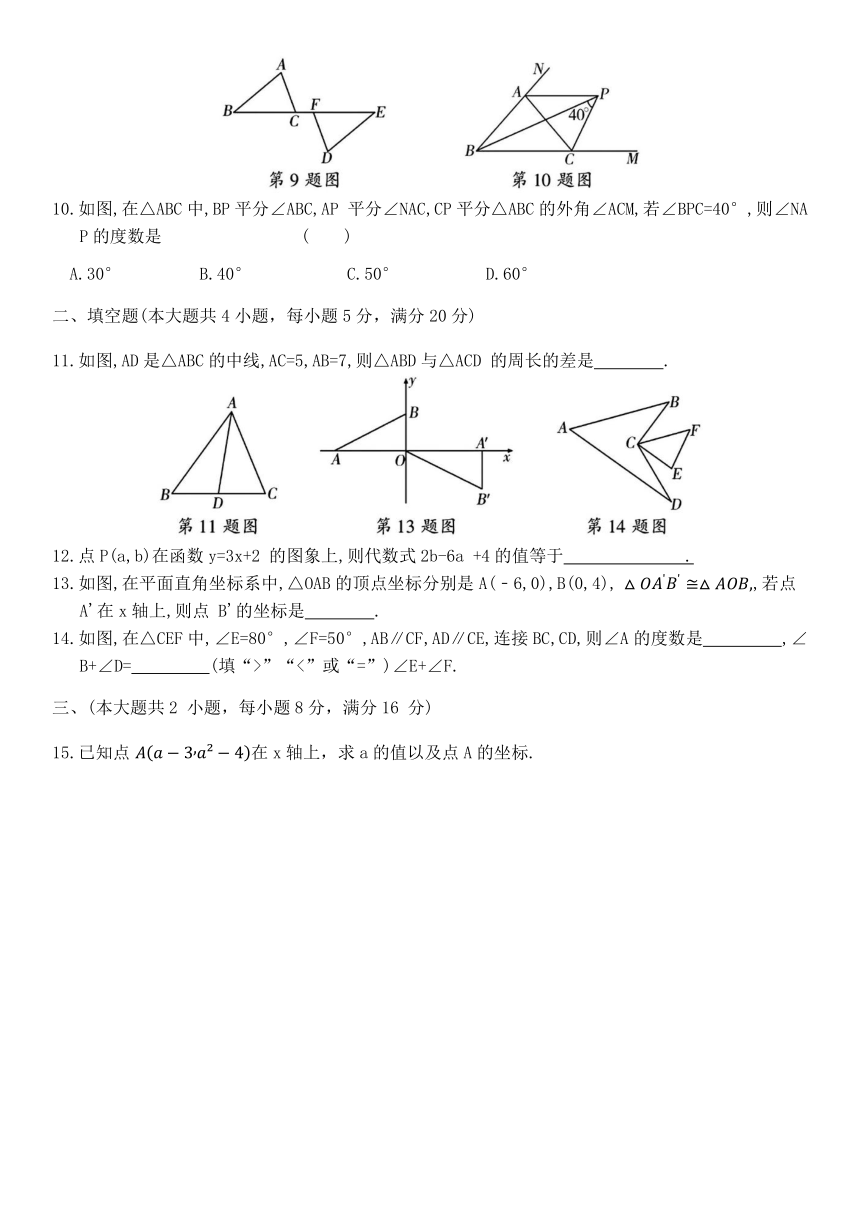
10.如图,在△ABC中,BP平分∠ABC,AP 平分∠NAC,CP平分△ABC的外角∠ACM,若∠BPC=40°,则∠NAP的度数是 ( )
A.30° B.40° C.50° D.60°
二、填空题(本大题共4小题,每小题5分,满分20分)
11.如图,AD是△ABC的中线,AC=5,AB=7,则△ABD与△ACD 的周长的差是 .
12.点P(a,b)在函数y=3x+2 的图象上,则代数式2b-6a +4的值等于 .
13.如图,在平面直角坐标系中,△OAB的顶点坐标分别是A(﹣6,0),B(0,4), ,若点 A'在x轴上,则点 B'的坐标是 .
14.如图,在△CEF中,∠E=80°,∠F=50°,AB∥CF,AD∥CE,连接BC,CD,则∠A的度数是 ,∠B+∠D= (填“>”“<”或“=”)∠E+∠F.
三、(本大题共2 小题,每小题8分,满分16 分)
15.已知点 在x轴上,求a的值以及点A的坐标.
16.在平面直角坐标系中有三点A( -1,1),B(3,1),C(2,3).
(1)在坐标系内描出点A,B,C的位置,顺次连接成
(2)把 向左平移4个单位,再向下平移3 个单位得到 画出 并写出点 的坐标.
四、(本大题共2 小题,每小题8分,满分16 分)
17.1805年,法国拿破仑率军与德军在莱茵河激战,德军在河北岸Q 处,如图.因不知河宽,法军很难瞄准敌军,聪明的拿破仑站在南岸O处调整好自己的帽子,使视线恰好擦过帽舌边沿看到敌军兵营Q处,然后后退到B点,这时他的视点恰好能落在O处,于是他命令部下测量他脚站的B处与O点之间的距离,并下令按这个距离炮轰敌兵营,法军能命中吗 说明理由.
18.在一个单位为1的方格纸上,有一列点. (其中n为正整数),均为网格上的格点,按如图所示规律排列,点的坐标分别为
(1)写出点 的坐标;
(2)总结在x轴上的点. 的坐标规律,并写出点 的坐标.
五、(本大题共2 小题,每小题 10 分,满分20 分)
19.如图,点 D 为. 的边 BC 的延长线上一点.
(1)若 求 的度数;
(2)若 的平分线与 的平分线交于点 M,过点 C 作于点 P.试探究 与 的数量关系.
20.九年级学生到距离学校6千米的百花公园去春游,一部分学生步行前往,20分钟后另一部分学生骑自行车前往,设x(分钟)为步行前往的学生离开学校所走的时间,步行学生走的路程为y 千米,骑自行车学生骑 行的路程为y 千米,y ,y 关于x的函数图象如图所示.
(1)求y 关于x的函数表达式;
(2)步行的学生和骑自行车的学生谁先到达百花公园,先到了几分钟
六、(本题满分12分)
21.已知. 的三条角平分线相交于点I,过点I作 交AC 于点 D.
(1)如图1,求证:
(2)如图2,延长BI,交外角. 的平分线于点 F.
①判断 DI 与 CF 的位置关系,并说明理由;
②若 求 的度数.
七、(本题满分12分)
22.如图,在 中, ,点 D 在直线 BC 上移动(不与点 B,C 重合),以AD 为一边在AB 的右侧作 使 连接CE,设
(1)如图1,点 D 在线段BC 上,求证:
(2)如图1,点D 在线段BC 上,请你探索α与β之间的数量关系,并证明你的结论;
(3)如图2,点D 在线段CB的延长线上,请写出α和β之间的数量关系.(直接写出结果)
八、(本题满分14分)
23.如图,直线AB与x轴、y轴分别交于A( -6,0),B(0,3)两点,在y轴上有一点N(0,6),动点 M从点 A 以每秒1个单位的速度沿x轴向右移动.
(1)求直线 AB 的函数表达式;
(2)求 的面积S与点M的移动时间t之间的函数表达式;
(3)当 时,求t的值与点M的坐标.
月考检测卷(二)
1. D 2. B 3. C 4. D 5. A 6. C 7. B 8. C 9. A 10. C
11.2 12.8 13.(6,-4) 14.50° <
15.解:∵点. 在x轴上,∴
当a=2时,a-3=-1.∴点A的坐标为(-1,0).
当a=-2时,a-3=-5.∴点A的坐标为( -5,0).
故a的值为±2.点A的坐标为( -1,0)或( -5,0).
16.解:(1)描点及△ABC如图.
(2)如图, 即为所求.
根据图象,得
17.解:法军能命中.理由如下:
根据题意,得AB=PO,∠A=∠P.
又∵AB⊥BO,PO⊥BQ,∴∠ABO=∠POQ=90°.
在△ABO和△POQ中,∵∠A=∠P,AB=PO,∠ABO=∠POQ=90°.
∴△ABO≌△POQ(ASA).∴BO=OQ.
因此,按照BO的距离炮轰德军时,炮弹恰好落入德军Q处.故法军能命中目标.
18.解:(1)点A 的坐标为(1,-5).
(2)观察发现:A (2,0),A (4,0),A (6,0),……,
A (0,0),A (-2,0),A (-4,0),…
∴A4n+1(2n+2,0),A4n-1(-2n+2,0)(n为自然数).
∵2021=505×4+1,∴A 的坐标为(1012,0).
19.解:(1)∵∠A:∠ABC=3:4,∴设∠A=3k,∠ABC=4k.
又∵∠ACD=∠A+∠ABC=140°,
∴3k+4k=140°.解得k=20°.∴∠A=3k=60°.
(2)∵∠MCD是△MBC的外角,∴∠M=∠MCD-∠MBC.
同理可得,∠A=∠ACD-∠ABC.
∵ CM,BM 分别平分
20.解:(1)设y 关于x的函数表达式是y =kx+b.
根据题意,得 解得
∴y 关于x的函数表达式是y =0.2x-4.
(2)由图象可知,步行的学生的速度为4÷40=0.1(千米/分钟).
∴步行同学到达百花公园的时间为6÷0.1=60(分钟).
当y =6时,6=0.2x-4.解得x=50.∵50<60,∴60-50=10(分钟).
答:骑自行车的学生先到达百花公园,先到了10 分钟.
21.(1)证明:∵ AI,BI分别平分∠BAC,∠ABC,
∴在△ABI中, 上
∵ CI平分 .
(2)解:①DI∥CF.理由如下:
CF平分∠ACE,
∴∠IDC=∠ACF.∴DI∥CF.
②∵∠ACE=∠ABC+∠BAC,∴∠ACE--∠ABC=∠BAC=70°.
∵∠FCE=∠FBC+∠F,∴∠F=∠FCE--∠FBC.
22.(1)证明:∵∠BAC=∠BAD+∠DAC,∠DAE=∠DAC+∠CAE,∠BAC=∠DAE,∴∠BAD =∠CAE.
在△ABD 和△ACE中,
(2)解:α+β=180°.证明如下:由(1)知,△ABD≌△ACE.∴∠ACE=∠B,又∠B+∠ACB+α=180°,∴∠ACE+∠ACB+α=180°.
又∵∠ACE+∠ACB=∠DCE=β,∴α+β=180°.
(3)解:α与β之间的数量关系是α=β.
23.解:(1)设直线AB的函数表达式为y=kx+b.将点A,B的坐标代入,得 解得 直线AB的函数表达式为
(2)分为两种情况讨论:
当点 M位于线段OA上时,即当0≤t≤6时,OM=OA-AM=6-t.
故
当点 M位于点O的右边时,即当t>6时,OM=AM-OA=t-6.
故
(3)在△MON与△BOA中,OA=ON=6,∠AOB=∠MON=90°.
当OM=OB时,△NOM≌△AOB(SAS).
分为两种情况讨论:
当点M位于线段OA上时,OM=OB=3,则AM=OA-OM=6-3=3.
此时t=3,点M的坐标为(-3,0).
当点M位于点O的右边时,OM=OB=3,则AM=OA+OM=6+3=9.
此时t=9,点M的坐标为(3,0).
(时间:120分钟满分:150分)
题 号 一 二 三 四 五 六 七 八 总 分
得 分
一、选择题(本大题共10 小题,每小题4分,满分40 分)
1.确定平面直角坐标系内点的位置是 ( )
A.一个实数 B.一个整数 C.一对实数 D.有序实数对
2.下列长度的三条线段,能构成三角形的是 ( )
A.1,2,3 B.3,4,5 C.5,12,17 D.6,8,20
3.下列函数①y=-5x;②y=-2x+1;③y= ;④y= x+6;⑤y=x -1中,是一次函数的有( )
A.1个 B.2个 C.3个 D.4个
4.下列命题为真命题的是 ( )
A.若|x|=|y|,则x=y
B.若a>b,则 ac>bc
C.任何一个角都比它的补角小
D.三角形的三条中线相交于一点
5.如图,将∠A,∠1,∠2的大小排列正确的是 ( )
A.∠1 >∠2 >∠A B.∠1>∠A>∠2
C.∠A>∠1 >∠2 D.∠2>∠1 >∠A
6.一个三角形的两边长为6和8,第三边长为偶数,则第三边长的最大值为( )
A.5 B.9 C.12 D.14
7.如图,D是AB上一点,DF交AC于点E,DE=FE,FC∥AB,若AB=4,CF=3,则BD的长是( )
A.0.5 B.1 C.1.5 D.2
8.若直线y=kx+b经过点(3,0),( 则kx+b >0 的解集是( )
B. x<3
C. x>3
9.如图,∠ACB=∠DFE,BC=EF,如果要使得△ABC≌△DEF,则还须补充的一个条件可以是( )
A.∠ABC =∠DEF B.∠ACE=∠DFB
C. BF=EC D. AB =DE
10.如图,在△ABC中,BP平分∠ABC,AP 平分∠NAC,CP平分△ABC的外角∠ACM,若∠BPC=40°,则∠NAP的度数是 ( )
A.30° B.40° C.50° D.60°
二、填空题(本大题共4小题,每小题5分,满分20分)
11.如图,AD是△ABC的中线,AC=5,AB=7,则△ABD与△ACD 的周长的差是 .
12.点P(a,b)在函数y=3x+2 的图象上,则代数式2b-6a +4的值等于 .
13.如图,在平面直角坐标系中,△OAB的顶点坐标分别是A(﹣6,0),B(0,4), ,若点 A'在x轴上,则点 B'的坐标是 .
14.如图,在△CEF中,∠E=80°,∠F=50°,AB∥CF,AD∥CE,连接BC,CD,则∠A的度数是 ,∠B+∠D= (填“>”“<”或“=”)∠E+∠F.
三、(本大题共2 小题,每小题8分,满分16 分)
15.已知点 在x轴上,求a的值以及点A的坐标.
16.在平面直角坐标系中有三点A( -1,1),B(3,1),C(2,3).
(1)在坐标系内描出点A,B,C的位置,顺次连接成
(2)把 向左平移4个单位,再向下平移3 个单位得到 画出 并写出点 的坐标.
四、(本大题共2 小题,每小题8分,满分16 分)
17.1805年,法国拿破仑率军与德军在莱茵河激战,德军在河北岸Q 处,如图.因不知河宽,法军很难瞄准敌军,聪明的拿破仑站在南岸O处调整好自己的帽子,使视线恰好擦过帽舌边沿看到敌军兵营Q处,然后后退到B点,这时他的视点恰好能落在O处,于是他命令部下测量他脚站的B处与O点之间的距离,并下令按这个距离炮轰敌兵营,法军能命中吗 说明理由.
18.在一个单位为1的方格纸上,有一列点. (其中n为正整数),均为网格上的格点,按如图所示规律排列,点的坐标分别为
(1)写出点 的坐标;
(2)总结在x轴上的点. 的坐标规律,并写出点 的坐标.
五、(本大题共2 小题,每小题 10 分,满分20 分)
19.如图,点 D 为. 的边 BC 的延长线上一点.
(1)若 求 的度数;
(2)若 的平分线与 的平分线交于点 M,过点 C 作于点 P.试探究 与 的数量关系.
20.九年级学生到距离学校6千米的百花公园去春游,一部分学生步行前往,20分钟后另一部分学生骑自行车前往,设x(分钟)为步行前往的学生离开学校所走的时间,步行学生走的路程为y 千米,骑自行车学生骑 行的路程为y 千米,y ,y 关于x的函数图象如图所示.
(1)求y 关于x的函数表达式;
(2)步行的学生和骑自行车的学生谁先到达百花公园,先到了几分钟
六、(本题满分12分)
21.已知. 的三条角平分线相交于点I,过点I作 交AC 于点 D.
(1)如图1,求证:
(2)如图2,延长BI,交外角. 的平分线于点 F.
①判断 DI 与 CF 的位置关系,并说明理由;
②若 求 的度数.
七、(本题满分12分)
22.如图,在 中, ,点 D 在直线 BC 上移动(不与点 B,C 重合),以AD 为一边在AB 的右侧作 使 连接CE,设
(1)如图1,点 D 在线段BC 上,求证:
(2)如图1,点D 在线段BC 上,请你探索α与β之间的数量关系,并证明你的结论;
(3)如图2,点D 在线段CB的延长线上,请写出α和β之间的数量关系.(直接写出结果)
八、(本题满分14分)
23.如图,直线AB与x轴、y轴分别交于A( -6,0),B(0,3)两点,在y轴上有一点N(0,6),动点 M从点 A 以每秒1个单位的速度沿x轴向右移动.
(1)求直线 AB 的函数表达式;
(2)求 的面积S与点M的移动时间t之间的函数表达式;
(3)当 时,求t的值与点M的坐标.
月考检测卷(二)
1. D 2. B 3. C 4. D 5. A 6. C 7. B 8. C 9. A 10. C
11.2 12.8 13.(6,-4) 14.50° <
15.解:∵点. 在x轴上,∴
当a=2时,a-3=-1.∴点A的坐标为(-1,0).
当a=-2时,a-3=-5.∴点A的坐标为( -5,0).
故a的值为±2.点A的坐标为( -1,0)或( -5,0).
16.解:(1)描点及△ABC如图.
(2)如图, 即为所求.
根据图象,得
17.解:法军能命中.理由如下:
根据题意,得AB=PO,∠A=∠P.
又∵AB⊥BO,PO⊥BQ,∴∠ABO=∠POQ=90°.
在△ABO和△POQ中,∵∠A=∠P,AB=PO,∠ABO=∠POQ=90°.
∴△ABO≌△POQ(ASA).∴BO=OQ.
因此,按照BO的距离炮轰德军时,炮弹恰好落入德军Q处.故法军能命中目标.
18.解:(1)点A 的坐标为(1,-5).
(2)观察发现:A (2,0),A (4,0),A (6,0),……,
A (0,0),A (-2,0),A (-4,0),…
∴A4n+1(2n+2,0),A4n-1(-2n+2,0)(n为自然数).
∵2021=505×4+1,∴A 的坐标为(1012,0).
19.解:(1)∵∠A:∠ABC=3:4,∴设∠A=3k,∠ABC=4k.
又∵∠ACD=∠A+∠ABC=140°,
∴3k+4k=140°.解得k=20°.∴∠A=3k=60°.
(2)∵∠MCD是△MBC的外角,∴∠M=∠MCD-∠MBC.
同理可得,∠A=∠ACD-∠ABC.
∵ CM,BM 分别平分
20.解:(1)设y 关于x的函数表达式是y =kx+b.
根据题意,得 解得
∴y 关于x的函数表达式是y =0.2x-4.
(2)由图象可知,步行的学生的速度为4÷40=0.1(千米/分钟).
∴步行同学到达百花公园的时间为6÷0.1=60(分钟).
当y =6时,6=0.2x-4.解得x=50.∵50<60,∴60-50=10(分钟).
答:骑自行车的学生先到达百花公园,先到了10 分钟.
21.(1)证明:∵ AI,BI分别平分∠BAC,∠ABC,
∴在△ABI中, 上
∵ CI平分 .
(2)解:①DI∥CF.理由如下:
CF平分∠ACE,
∴∠IDC=∠ACF.∴DI∥CF.
②∵∠ACE=∠ABC+∠BAC,∴∠ACE--∠ABC=∠BAC=70°.
∵∠FCE=∠FBC+∠F,∴∠F=∠FCE--∠FBC.
22.(1)证明:∵∠BAC=∠BAD+∠DAC,∠DAE=∠DAC+∠CAE,∠BAC=∠DAE,∴∠BAD =∠CAE.
在△ABD 和△ACE中,
(2)解:α+β=180°.证明如下:由(1)知,△ABD≌△ACE.∴∠ACE=∠B,又∠B+∠ACB+α=180°,∴∠ACE+∠ACB+α=180°.
又∵∠ACE+∠ACB=∠DCE=β,∴α+β=180°.
(3)解:α与β之间的数量关系是α=β.
23.解:(1)设直线AB的函数表达式为y=kx+b.将点A,B的坐标代入,得 解得 直线AB的函数表达式为
(2)分为两种情况讨论:
当点 M位于线段OA上时,即当0≤t≤6时,OM=OA-AM=6-t.
故
当点 M位于点O的右边时,即当t>6时,OM=AM-OA=t-6.
故
(3)在△MON与△BOA中,OA=ON=6,∠AOB=∠MON=90°.
当OM=OB时,△NOM≌△AOB(SAS).
分为两种情况讨论:
当点M位于线段OA上时,OM=OB=3,则AM=OA-OM=6-3=3.
此时t=3,点M的坐标为(-3,0).
当点M位于点O的右边时,OM=OB=3,则AM=OA+OM=6+3=9.
此时t=9,点M的坐标为(3,0).
同课章节目录
