沪科版数学八年级上册第 15章 轴对称图形与等腰三角形 知识分类练(无答案)
文档属性
| 名称 | 沪科版数学八年级上册第 15章 轴对称图形与等腰三角形 知识分类练(无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-07 14:52:29 | ||
图片预览


文档简介
第 15章 轴对称图形与等腰三角形
考点一 轴对称图形
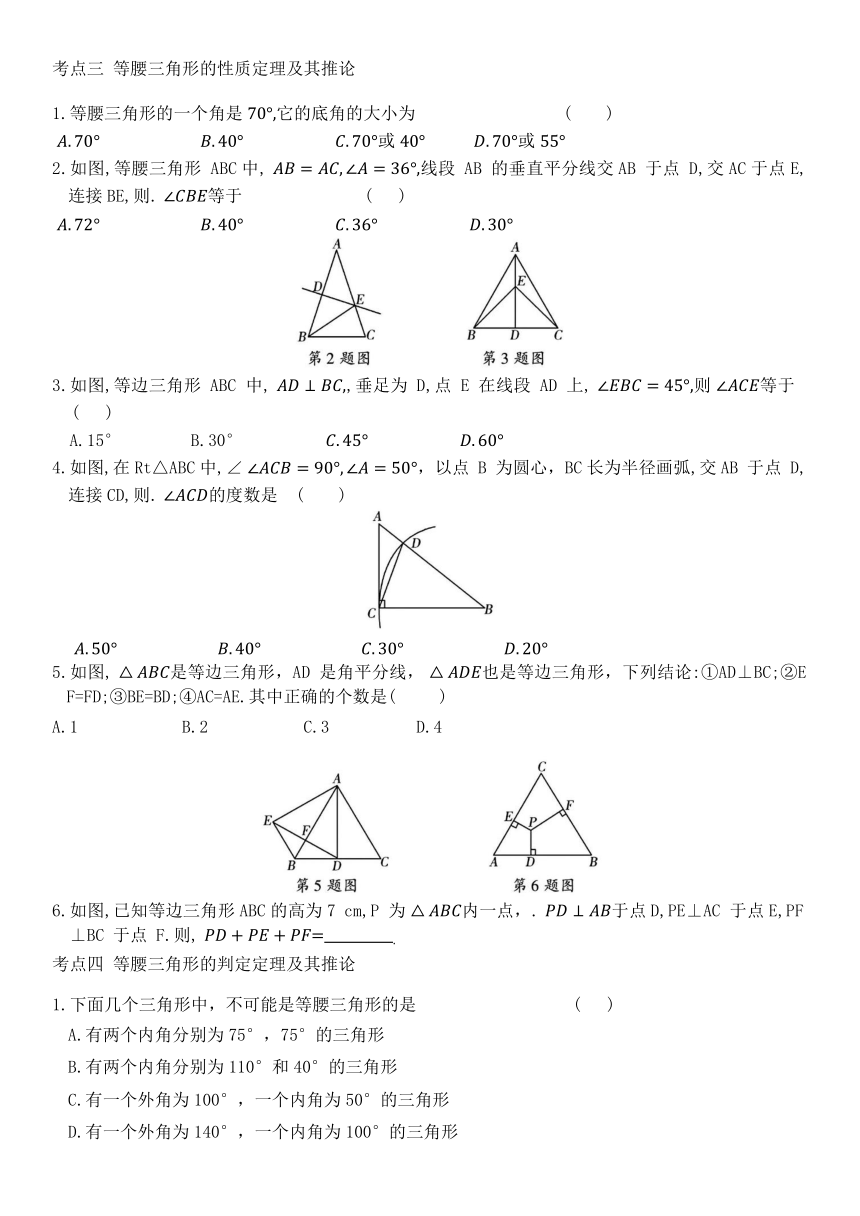
1.下列图形中是轴对称图形且有两条对称轴的是 ( )
A.①② B.②③ C.②④ D.③④
2.如图所示的四组图形中,成轴对称的是 ( )
3.如图,△ABC与△A'B'C'关于直线l对称,且. 则∠B的度数为 ( )
A.48° B.54° C.74° D.78°
4.在平面直角坐标系中,点A(m,2)与点B(3,n)关于y轴对称,则 ( )
A. m=3,n=2 B. m= -3,n=2
C. m=2,n=3 D. m= -2,n= -3
5.如图,已知△ABC的两条边AC=8,BC=6,现将△ABC沿DE 折叠,使点A 与点 B重合,则△BCE的周长是 ( )
A.10 B.12 C.14 D.22
6.已知点A(m+1,3)与点B(2,n-1)关于x轴对称,则 的值为
7.如图,在平面直角坐标系中,已知△ABC 的三个顶点坐标分别是A(2,-1),B(1,-2),C(3,-3).
(1)将 向上平移3 个单位得到 ,请画出
(2)请画出与 关于y轴对称的
(3)请写出点 的坐标.
考点二 线段的垂直平分线
1.如图所示的尺规作图是作 ( )
A.线段的垂直平分线
B.一个半径为定值的圆
C.一条直线的平行线
D.一个角等于已知角
2.如图,直线CD 是线段AB的垂直平分线,点P 为直线 CD上的一点,已知线段 ,则线段 PB的长度为 ( )
A.6 B.5 C.4 D.3
3.如图,CD 是 AB 的垂直平分线,若 ,则四边形ACBD 的周长为 ( )
A.3.9 cm B.7. 8cm C.4 cm D.4.6 cm
4.如图,有A,B,C三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在 ( )
A. AC,BC两边高线的交点处
B. AC,BC两边中线的交点处
C. AC,BC 两边垂直平分线的交点处
两内角平分线的交点处
5.尺规作图:如图,已知 ,请在 AC 边上找一点 D,使 的周长等于 .(保留作图痕迹,不写作法)
6.如图,点D 是 的边BC上一点, 于点E, 于点F,并且 连接AD,EF.求证:AD垂直平分EF.
考点三 等腰三角形的性质定理及其推论
1.等腰三角形的一个角是它的底角的大小为 ( )
或 或
2.如图,等腰三角形 ABC中, 线段 AB 的垂直平分线交AB 于点 D,交AC于点E,连接BE,则. 等于 ( )
3.如图,等边三角形 ABC 中, ,垂足为 D,点 E 在线段 AD 上, 则 等于 ( )
A.15° B.30°
4.如图,在Rt△ABC中,∠ ,以点 B 为圆心,BC长为半径画弧,交AB 于点 D,连接CD,则. 的度数是 ( )
5.如图, 是等边三角形,AD 是角平分线, 也是等边三角形,下列结论:①AD⊥BC;②EF=FD;③BE=BD;④AC=AE.其中正确的个数是( )
A.1 B.2 C.3 D.4
6.如图,已知等边三角形ABC的高为7 cm,P 为 内一点,. 于点D,PE⊥AC 于点E,PF⊥BC 于点 F.则,
考点四 等腰三角形的判定定理及其推论
1.下面几个三角形中,不可能是等腰三角形的是 ( )
A.有两个内角分别为75°,75°的三角形
B.有两个内角分别为110°和40°的三角形
C.有一个外角为100°,一个内角为50°的三角形
D.有一个外角为140°,一个内角为100°的三角形
2.如图,△ABC中,∠A=36°,AB=AC,BD平分∠ABC,则图中等腰三角形有( )
A.1个 B.2个 C.3个 D.4个
3.在△ABC中,①AB=BC=CA;②有一个角为60°的三角形;③顶角为60°的等腰三角形,上述条件中能判定此三角形为等边三角形的有 ( )
A.1 个 B.2个 C.3个 D.0个
4.如图,在△ABC中,AB=AC=5,D是BC上的点,DE∥AB交AC于点E,DF∥AC 交AB于点F,那么四边形AFDE 的周长是 ( )
A.5 B.10 C.15 D.20
5.如图,△ABC 中,点 D 在 BC 的延长线上,∠A =60°,∠ACD =120°,则△ABC 是 三角形.
如图,在 中, 于点 D, 的平分线交AD 于点 E,交AB 于点 F,
试判断 的形状,并说明理由.
考点五 含 角的直角三角形的性质定理
1.如图,在等腰三角形ABC 中, ,D 为 AC 边的中点.若 ,则BD的长为 ( )
A.3 B.4 C.6 D.8
2.如图,一场暴雨过后,垂直于地面的一棵树在距地面3m 处折断,树尖B恰好碰到地面,经测量 ,则树高为 ( )
A.6m B.9m C.10m D.12 m
3.如图,在. 中, ,AB 的垂直平分线 ED 交 AB 于点E,交 BC 于点 D,若 ,则BD 的长为 .
4.如图,在 中, ,AD 平分 求CD的长.
考点六 角的平分线
1.已知∠AOB,求作射线OC,使OC平分∠AOB,作图的合理顺序是 ( )①作射线OC;②在OA 和 OB上分别截取OD,OE,使 ③分别以点D,E为圆心,以大于 的长为半径,在∠AOB 内画弧交于点 C.
A.①②③ B.②①③ C.②③① D.③②①
2.用尺规作图作已知角的平分线的理论依据是 ( )
A. SAS B. AAS C. SSS D. ASA
3.如图,OP为∠AOB的平分线,PC⊥OA,PD⊥OB,垂足分别为C,D,则下列结论错误的是 ( )
A. PC=PD
B.∠CPO=∠DOP
C.∠CPO=∠DPO
D. OC=OD
4.到三角形三边距离相等的点,是这个三角形的 ( )
A.三条高的交点 B.三条中线的交点
C.三条角平分线的交点 D.三边垂直平分线的交点
5.如图,已知AB∥CD,O是∠ACD,∠CAB的平分线的交点,且OE⊥AC于E点,OE=12,则AB 与 CD 之间的距离为 ( )
A.12 B.18 C.24 D.无法确定
6.已知点O在直线AB上,过点O作OC⊥AB,如图,请根据图形填空.
作法:(1)作∠ 的平分线 ;(2)直线 即为所求.
7.如图,已知BD⊥AE 于点 B,DC⊥AF 于点C,且DB =DC,∠BAC=40°,∠ADG=130°,则∠DGF = .
8.如图,在Rt△ABC中,AD平分∠BAC交BC于点D,若BD:CD=3:2,点D到AB的距离是6,则BC= .
考点一 轴对称图形
1.下列图形中是轴对称图形且有两条对称轴的是 ( )
A.①② B.②③ C.②④ D.③④
2.如图所示的四组图形中,成轴对称的是 ( )
3.如图,△ABC与△A'B'C'关于直线l对称,且. 则∠B的度数为 ( )
A.48° B.54° C.74° D.78°
4.在平面直角坐标系中,点A(m,2)与点B(3,n)关于y轴对称,则 ( )
A. m=3,n=2 B. m= -3,n=2
C. m=2,n=3 D. m= -2,n= -3
5.如图,已知△ABC的两条边AC=8,BC=6,现将△ABC沿DE 折叠,使点A 与点 B重合,则△BCE的周长是 ( )
A.10 B.12 C.14 D.22
6.已知点A(m+1,3)与点B(2,n-1)关于x轴对称,则 的值为
7.如图,在平面直角坐标系中,已知△ABC 的三个顶点坐标分别是A(2,-1),B(1,-2),C(3,-3).
(1)将 向上平移3 个单位得到 ,请画出
(2)请画出与 关于y轴对称的
(3)请写出点 的坐标.
考点二 线段的垂直平分线
1.如图所示的尺规作图是作 ( )
A.线段的垂直平分线
B.一个半径为定值的圆
C.一条直线的平行线
D.一个角等于已知角
2.如图,直线CD 是线段AB的垂直平分线,点P 为直线 CD上的一点,已知线段 ,则线段 PB的长度为 ( )
A.6 B.5 C.4 D.3
3.如图,CD 是 AB 的垂直平分线,若 ,则四边形ACBD 的周长为 ( )
A.3.9 cm B.7. 8cm C.4 cm D.4.6 cm
4.如图,有A,B,C三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在 ( )
A. AC,BC两边高线的交点处
B. AC,BC两边中线的交点处
C. AC,BC 两边垂直平分线的交点处
两内角平分线的交点处
5.尺规作图:如图,已知 ,请在 AC 边上找一点 D,使 的周长等于 .(保留作图痕迹,不写作法)
6.如图,点D 是 的边BC上一点, 于点E, 于点F,并且 连接AD,EF.求证:AD垂直平分EF.
考点三 等腰三角形的性质定理及其推论
1.等腰三角形的一个角是它的底角的大小为 ( )
或 或
2.如图,等腰三角形 ABC中, 线段 AB 的垂直平分线交AB 于点 D,交AC于点E,连接BE,则. 等于 ( )
3.如图,等边三角形 ABC 中, ,垂足为 D,点 E 在线段 AD 上, 则 等于 ( )
A.15° B.30°
4.如图,在Rt△ABC中,∠ ,以点 B 为圆心,BC长为半径画弧,交AB 于点 D,连接CD,则. 的度数是 ( )
5.如图, 是等边三角形,AD 是角平分线, 也是等边三角形,下列结论:①AD⊥BC;②EF=FD;③BE=BD;④AC=AE.其中正确的个数是( )
A.1 B.2 C.3 D.4
6.如图,已知等边三角形ABC的高为7 cm,P 为 内一点,. 于点D,PE⊥AC 于点E,PF⊥BC 于点 F.则,
考点四 等腰三角形的判定定理及其推论
1.下面几个三角形中,不可能是等腰三角形的是 ( )
A.有两个内角分别为75°,75°的三角形
B.有两个内角分别为110°和40°的三角形
C.有一个外角为100°,一个内角为50°的三角形
D.有一个外角为140°,一个内角为100°的三角形
2.如图,△ABC中,∠A=36°,AB=AC,BD平分∠ABC,则图中等腰三角形有( )
A.1个 B.2个 C.3个 D.4个
3.在△ABC中,①AB=BC=CA;②有一个角为60°的三角形;③顶角为60°的等腰三角形,上述条件中能判定此三角形为等边三角形的有 ( )
A.1 个 B.2个 C.3个 D.0个
4.如图,在△ABC中,AB=AC=5,D是BC上的点,DE∥AB交AC于点E,DF∥AC 交AB于点F,那么四边形AFDE 的周长是 ( )
A.5 B.10 C.15 D.20
5.如图,△ABC 中,点 D 在 BC 的延长线上,∠A =60°,∠ACD =120°,则△ABC 是 三角形.
如图,在 中, 于点 D, 的平分线交AD 于点 E,交AB 于点 F,
试判断 的形状,并说明理由.
考点五 含 角的直角三角形的性质定理
1.如图,在等腰三角形ABC 中, ,D 为 AC 边的中点.若 ,则BD的长为 ( )
A.3 B.4 C.6 D.8
2.如图,一场暴雨过后,垂直于地面的一棵树在距地面3m 处折断,树尖B恰好碰到地面,经测量 ,则树高为 ( )
A.6m B.9m C.10m D.12 m
3.如图,在. 中, ,AB 的垂直平分线 ED 交 AB 于点E,交 BC 于点 D,若 ,则BD 的长为 .
4.如图,在 中, ,AD 平分 求CD的长.
考点六 角的平分线
1.已知∠AOB,求作射线OC,使OC平分∠AOB,作图的合理顺序是 ( )①作射线OC;②在OA 和 OB上分别截取OD,OE,使 ③分别以点D,E为圆心,以大于 的长为半径,在∠AOB 内画弧交于点 C.
A.①②③ B.②①③ C.②③① D.③②①
2.用尺规作图作已知角的平分线的理论依据是 ( )
A. SAS B. AAS C. SSS D. ASA
3.如图,OP为∠AOB的平分线,PC⊥OA,PD⊥OB,垂足分别为C,D,则下列结论错误的是 ( )
A. PC=PD
B.∠CPO=∠DOP
C.∠CPO=∠DPO
D. OC=OD
4.到三角形三边距离相等的点,是这个三角形的 ( )
A.三条高的交点 B.三条中线的交点
C.三条角平分线的交点 D.三边垂直平分线的交点
5.如图,已知AB∥CD,O是∠ACD,∠CAB的平分线的交点,且OE⊥AC于E点,OE=12,则AB 与 CD 之间的距离为 ( )
A.12 B.18 C.24 D.无法确定
6.已知点O在直线AB上,过点O作OC⊥AB,如图,请根据图形填空.
作法:(1)作∠ 的平分线 ;(2)直线 即为所求.
7.如图,已知BD⊥AE 于点 B,DC⊥AF 于点C,且DB =DC,∠BAC=40°,∠ADG=130°,则∠DGF = .
8.如图,在Rt△ABC中,AD平分∠BAC交BC于点D,若BD:CD=3:2,点D到AB的距离是6,则BC= .
