沪科版数学八年级上册第十五 章 轴对称图形与等腰三角形 单元练习卷(含答案)
文档属性
| 名称 | 沪科版数学八年级上册第十五 章 轴对称图形与等腰三角形 单元练习卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-07 14:54:25 | ||
图片预览

文档简介
第十五 章 轴对称图形与等腰三角形
(时间:120分钟 满分:150分)
题 号 一 二 三 四 五 六 七 八 总分
得 分
一、选择题(本大题共10 小题,每小题4分,满分40 分)
1.下列图形中,对称轴的条数最少的图形是 ( )
2.点 关于y轴对称的点的坐标是 ( )
A.(4,-3) B.( -4,3) C.(4,3) D.(-3,4)
3.若 则以a,b为边长的等腰三角形的周长为( )
A.6 B.7 C.8 D.7或8
4.如图,在△ABC中, ,AD平分∠CAB,DE⊥AB 于点 E, 则△DEB的周长为 ( )
A.6 B.8 C.10 D.12
5.如图,在△ABC 中, ,观察图中尺规作图的痕迹,可知∠BCG的度数为 ( )
A.40° B.45° C.50° D.60°
6.如图, 为了使白球反弹后能将黑球直接撞入袋中,那么击打白球时,必须保证∠1 的度数为 ( )
B.45° C.60° D.75°
7.如图,在 中, ,分别以点A 和点 C 为圆心,大于 的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD,则. 的度数为 ( )
A.65° B.60° C.55° D.45°
8.已知等腰三角形一腰上的高线与另一腰的夹角为: ,那么这个等腰三角形的顶角等于( )
A.15°或75° B.140° C.40° D.140°或40°
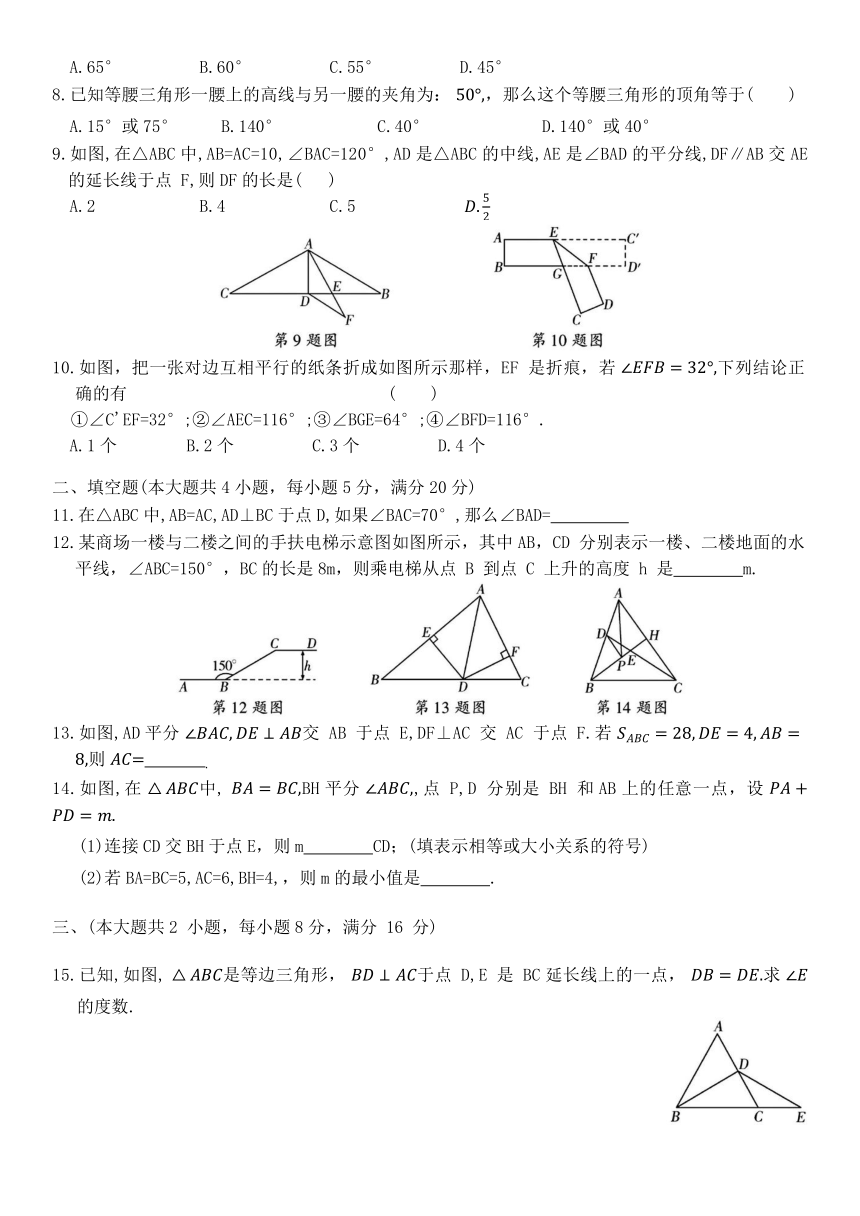
9.如图,在△ABC中,AB=AC=10,∠BAC=120°,AD是△ABC的中线,AE是∠BAD的平分线,DF∥AB交AE的延长线于点 F,则DF的长是( )
A.2 B.4 C.5
10.如图,把一张对边互相平行的纸条折成如图所示那样,EF 是折痕,若 下列结论正确的有 ( )
①∠C'EF=32°;②∠AEC=116°;③∠BGE=64°;④∠BFD=116°.
A.1个 B.2个 C.3个 D.4个
二、填空题(本大题共4小题,每小题5分,满分20分)
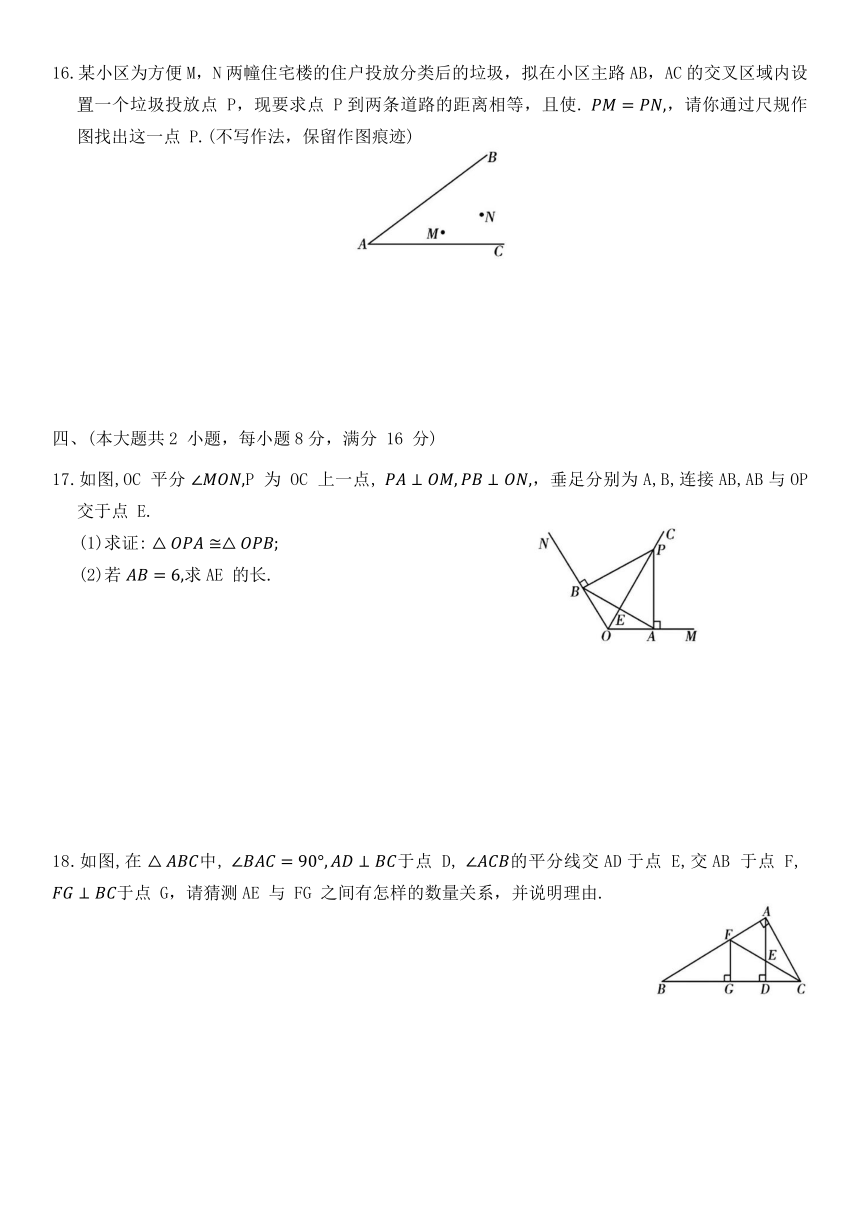
11.在△ABC中,AB=AC,AD⊥BC于点D,如果∠BAC=70°,那么∠BAD=
12.某商场一楼与二楼之间的手扶电梯示意图如图所示,其中AB,CD 分别表示一楼、二楼地面的水平线,∠ABC=150°,BC的长是8m,则乘电梯从点 B 到点 C 上升的高度 h 是 m.
13.如图,AD平分 交 AB 于点 E,DF⊥AC 交 AC 于点 F.若 则
14.如图,在 中, BH平分 ,点 P,D 分别是 BH 和AB上的任意一点,设
(1)连接CD交BH于点E,则m CD;(填表示相等或大小关系的符号)
(2)若BA=BC=5,AC=6,BH=4,,则m的最小值是 .
三、(本大题共2 小题,每小题8分,满分 16 分)
15.已知,如图, 是等边三角形, 于点 D,E 是 BC延长线上的一点, 求 的度数.
16.某小区为方便M,N两幢住宅楼的住户投放分类后的垃圾,拟在小区主路AB,AC的交叉区域内设置一个垃圾投放点 P,现要求点 P到两条道路的距离相等,且使. ,请你通过尺规作图找出这一点 P.(不写作法,保留作图痕迹)
四、(本大题共2 小题,每小题8分,满分 16 分)
17.如图,OC 平分 P 为 OC 上一点, ,垂足分别为A,B,连接AB,AB与OP交于点 E.
(1)求证:
(2)若 求AE 的长.
18.如图,在 中, 于点 D, 的平分线交AD于点 E,交AB 于点 F, 于点 G,请猜测AE 与 FG 之间有怎样的数量关系,并说明理由.
五、(本大题共2 小题,每小题10 分,满分20 分)
19.如图,在 中,AD平分 ,BC的垂直平分线 DG交AD 于点 D, 于点E, 于点 F.求证:
20.如图,在 中, AD 平分 于点 E.
(1)若 求 的度数;
(2)求证:直线 AD 是线段 CE的垂直平分线.
六、(本题满分12 分)
21.在平面直角坐标系中, 的三个顶点的位置如图所示.
(1)请画出. 关于y轴对称的. (其中 分别是A,B,C的对应点,不写画法);
(2)直接写出 三点的坐标;
(3)求 的面积.
七、(本题满分12 分)
22.如图,在△ABC中,AB=AC,点 D,E,F分别在AB,BC,AC边上,且BE=CF,BD=CE.
(1)求证:△DEF是等腰三角形;
(2)当∠A=50°时,求∠DEF的度数;
(3)若∠A=∠DEF,判断△DEF是否为等边三角形.
八、(本题满分14 分)
23.如图,CD是△ABC的高,∠A=2∠B,∠ACB的平分线CE交AB于点E,设∠B=α(α≤36°).
(1)求∠DCE的度数(用含的代数式表示);
(2)求证:BC-BE=2DE;
(3)将△BCE沿直线BC折叠得到△BCF,连接AF,EF,若CF∥AB,求∠DCE的度数.
第十五 章 轴对称图形与等腰三角形
1. B 2. A 3. D 4. A 5. C 6. C 7. A 8. D 9. C 10. D
11.35° 12.4 13.6 14.(1)≥ (2)
15.解:∵ △ABC是等边三角形,∴∠ABC=60°.∵ BD⊥AC,∴∠DBC= ∠ABC=30°.∵DB=DE,∴∠E=∠DBC.∴∠E=30°.
16.解:如图,点 P 即为所求.
17.(1)证明:∵OC 平分∠MON,PA⊥OM,PB⊥ON,∴PA=PB.
在 和 中,(OP=PB,∴Rt△OPA≌Rt△OPB(HL).
(2)解:∵△OPA≌△OPB,∴OA=OB.
又∵ OE 平分
18.解: 理由如下:
∵ CF平分∠ACB,FG⊥CB,∠BAC=90°,∴FA=FG,∠ACE=∠BCE.
∵AD⊥BC,∠BAC=90°,∴∠ADC=∠BAC=90°.
∴∠BCE+∠DEC=90°,∠ACE+∠AFC=90°.∴∠AFC=∠DEC.
又∵∠DEC=∠AEF,∴∠AFE=∠AEF.∴AE=AF.
又∵AF=FG,∴AE=FG.
19.证明:(1)连接DB,DC,如图.
∵ DG 垂直平分 BC,∴ DB = DC.
∵AD 平分∠BAC,DE⊥AB,DF⊥AC,
在 Rt△BDE 和 中,
∴ Rt△BDE≌Rt△CDF(HL).∴ BE=CF.
(2)在 Rt△DAE 和 Rt△DAF中,
∴ Rt△DAE≌Rt△DAF(HL).∴AE=AF.
∵AB﹣AE=BE,∴AB﹣AF=CF.
∴AB-(AC+CF)=CF.∴AB-AC-CF=CF.∴AB-AC=2CF.
20.(1)解:∵ AD 平分∠
∵DE⊥AB,∴∠AED=90°.∴∠AED=90°-∠EAD=90°-25°=65°.
(2)证明:∵ DE⊥AB,∠ACD=90°,∴∠EDA=∠ACD=90°.
∵AD 平分∠BAC,∴∠DAE=∠DAC.
在△AED和△ACD 中,
∴AE=AC,DE=DC.
∴点A在线段CE的垂直平分线上,点D 在线段CE 的垂直平分线上.
∴直线AD 是线段CE的垂直平分线.
21.解:(1)如图,△A'B'C'即为所求.
(2)A'(2,3),B'(3,1),C'( -1,-2).
22.(1)证明:∵AB=AC,∴∠B=∠C.
在△BDE 和△CEF中,
∴DE=EF.∴△DEF 是等腰三角形.
(2)解:∵∠DEC=∠B+∠BDE,∠DEC=∠DEF+∠CEF,∴∠DEF+∠CEF=∠B+∠BDE.
∵△BDE≌△CEF,∴∠CEF=∠BDE.∴∠DEF=∠B.
又∵在△ABC中,AB=AC,∠A=50°,∴∠B=65°.∴∠DEF=65°.
(3)解:由(1)知,△DEF是等腰三角形,即DE=EF.
由(2)知,∠DEF=∠B.
∵∠A=∠DEF,∴∠A=∠B.∵AB=AC,∴∠B=∠C.
∴∠A=∠B=∠C.∴△ABC是等边三角形.
∴∠B=∠DEF=60°.∴△DEF是等边三角形.
23.(1)解:∵∠B=α,∠A=2∠B,∴∠A=2α.
∴∠ACB=180°-(∠A+∠B) =180°-3α.
∵ CE平分.
∵ CD是△ABC的高,∴∠ADC=90°.∴∠ACD=90°-∠A=90°-2α.
x
(2)证明:在 DA 上截取DM=DE,连接CM,如图.
α.
∴∠BMC=∠BCM.∴BC=BM.∴BM=BE+ME=BE+2DE.
∴BC=BE+2DE.∴BC-BE=2DE.
(3)解:∵△BCE沿直线 BC折叠得到△BCF,∴△BCE≌△BCF.
∴BE=BF,CE=CF,∠EBC=∠FBC,∠ECB=∠FCB.
∵CF∥AB,∴∠FCB=∠EBC.
∴∠FCB=∠FBC=∠ECB=∠EBC.∴CF=BF=BE=EC.
∴∠EBC=∠ECB=∠ACE=α.∴∠ACB=∠CAB=2α.
∴在△ABC中,2α+2α+α=180°.∴α=36°.∴∠DCE= α=18°.
(时间:120分钟 满分:150分)
题 号 一 二 三 四 五 六 七 八 总分
得 分
一、选择题(本大题共10 小题,每小题4分,满分40 分)
1.下列图形中,对称轴的条数最少的图形是 ( )
2.点 关于y轴对称的点的坐标是 ( )
A.(4,-3) B.( -4,3) C.(4,3) D.(-3,4)
3.若 则以a,b为边长的等腰三角形的周长为( )
A.6 B.7 C.8 D.7或8
4.如图,在△ABC中, ,AD平分∠CAB,DE⊥AB 于点 E, 则△DEB的周长为 ( )
A.6 B.8 C.10 D.12
5.如图,在△ABC 中, ,观察图中尺规作图的痕迹,可知∠BCG的度数为 ( )
A.40° B.45° C.50° D.60°
6.如图, 为了使白球反弹后能将黑球直接撞入袋中,那么击打白球时,必须保证∠1 的度数为 ( )
B.45° C.60° D.75°
7.如图,在 中, ,分别以点A 和点 C 为圆心,大于 的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD,则. 的度数为 ( )
A.65° B.60° C.55° D.45°
8.已知等腰三角形一腰上的高线与另一腰的夹角为: ,那么这个等腰三角形的顶角等于( )
A.15°或75° B.140° C.40° D.140°或40°
9.如图,在△ABC中,AB=AC=10,∠BAC=120°,AD是△ABC的中线,AE是∠BAD的平分线,DF∥AB交AE的延长线于点 F,则DF的长是( )
A.2 B.4 C.5
10.如图,把一张对边互相平行的纸条折成如图所示那样,EF 是折痕,若 下列结论正确的有 ( )
①∠C'EF=32°;②∠AEC=116°;③∠BGE=64°;④∠BFD=116°.
A.1个 B.2个 C.3个 D.4个
二、填空题(本大题共4小题,每小题5分,满分20分)
11.在△ABC中,AB=AC,AD⊥BC于点D,如果∠BAC=70°,那么∠BAD=
12.某商场一楼与二楼之间的手扶电梯示意图如图所示,其中AB,CD 分别表示一楼、二楼地面的水平线,∠ABC=150°,BC的长是8m,则乘电梯从点 B 到点 C 上升的高度 h 是 m.
13.如图,AD平分 交 AB 于点 E,DF⊥AC 交 AC 于点 F.若 则
14.如图,在 中, BH平分 ,点 P,D 分别是 BH 和AB上的任意一点,设
(1)连接CD交BH于点E,则m CD;(填表示相等或大小关系的符号)
(2)若BA=BC=5,AC=6,BH=4,,则m的最小值是 .
三、(本大题共2 小题,每小题8分,满分 16 分)
15.已知,如图, 是等边三角形, 于点 D,E 是 BC延长线上的一点, 求 的度数.
16.某小区为方便M,N两幢住宅楼的住户投放分类后的垃圾,拟在小区主路AB,AC的交叉区域内设置一个垃圾投放点 P,现要求点 P到两条道路的距离相等,且使. ,请你通过尺规作图找出这一点 P.(不写作法,保留作图痕迹)
四、(本大题共2 小题,每小题8分,满分 16 分)
17.如图,OC 平分 P 为 OC 上一点, ,垂足分别为A,B,连接AB,AB与OP交于点 E.
(1)求证:
(2)若 求AE 的长.
18.如图,在 中, 于点 D, 的平分线交AD于点 E,交AB 于点 F, 于点 G,请猜测AE 与 FG 之间有怎样的数量关系,并说明理由.
五、(本大题共2 小题,每小题10 分,满分20 分)
19.如图,在 中,AD平分 ,BC的垂直平分线 DG交AD 于点 D, 于点E, 于点 F.求证:
20.如图,在 中, AD 平分 于点 E.
(1)若 求 的度数;
(2)求证:直线 AD 是线段 CE的垂直平分线.
六、(本题满分12 分)
21.在平面直角坐标系中, 的三个顶点的位置如图所示.
(1)请画出. 关于y轴对称的. (其中 分别是A,B,C的对应点,不写画法);
(2)直接写出 三点的坐标;
(3)求 的面积.
七、(本题满分12 分)
22.如图,在△ABC中,AB=AC,点 D,E,F分别在AB,BC,AC边上,且BE=CF,BD=CE.
(1)求证:△DEF是等腰三角形;
(2)当∠A=50°时,求∠DEF的度数;
(3)若∠A=∠DEF,判断△DEF是否为等边三角形.
八、(本题满分14 分)
23.如图,CD是△ABC的高,∠A=2∠B,∠ACB的平分线CE交AB于点E,设∠B=α(α≤36°).
(1)求∠DCE的度数(用含的代数式表示);
(2)求证:BC-BE=2DE;
(3)将△BCE沿直线BC折叠得到△BCF,连接AF,EF,若CF∥AB,求∠DCE的度数.
第十五 章 轴对称图形与等腰三角形
1. B 2. A 3. D 4. A 5. C 6. C 7. A 8. D 9. C 10. D
11.35° 12.4 13.6 14.(1)≥ (2)
15.解:∵ △ABC是等边三角形,∴∠ABC=60°.∵ BD⊥AC,∴∠DBC= ∠ABC=30°.∵DB=DE,∴∠E=∠DBC.∴∠E=30°.
16.解:如图,点 P 即为所求.
17.(1)证明:∵OC 平分∠MON,PA⊥OM,PB⊥ON,∴PA=PB.
在 和 中,(OP=PB,∴Rt△OPA≌Rt△OPB(HL).
(2)解:∵△OPA≌△OPB,∴OA=OB.
又∵ OE 平分
18.解: 理由如下:
∵ CF平分∠ACB,FG⊥CB,∠BAC=90°,∴FA=FG,∠ACE=∠BCE.
∵AD⊥BC,∠BAC=90°,∴∠ADC=∠BAC=90°.
∴∠BCE+∠DEC=90°,∠ACE+∠AFC=90°.∴∠AFC=∠DEC.
又∵∠DEC=∠AEF,∴∠AFE=∠AEF.∴AE=AF.
又∵AF=FG,∴AE=FG.
19.证明:(1)连接DB,DC,如图.
∵ DG 垂直平分 BC,∴ DB = DC.
∵AD 平分∠BAC,DE⊥AB,DF⊥AC,
在 Rt△BDE 和 中,
∴ Rt△BDE≌Rt△CDF(HL).∴ BE=CF.
(2)在 Rt△DAE 和 Rt△DAF中,
∴ Rt△DAE≌Rt△DAF(HL).∴AE=AF.
∵AB﹣AE=BE,∴AB﹣AF=CF.
∴AB-(AC+CF)=CF.∴AB-AC-CF=CF.∴AB-AC=2CF.
20.(1)解:∵ AD 平分∠
∵DE⊥AB,∴∠AED=90°.∴∠AED=90°-∠EAD=90°-25°=65°.
(2)证明:∵ DE⊥AB,∠ACD=90°,∴∠EDA=∠ACD=90°.
∵AD 平分∠BAC,∴∠DAE=∠DAC.
在△AED和△ACD 中,
∴AE=AC,DE=DC.
∴点A在线段CE的垂直平分线上,点D 在线段CE 的垂直平分线上.
∴直线AD 是线段CE的垂直平分线.
21.解:(1)如图,△A'B'C'即为所求.
(2)A'(2,3),B'(3,1),C'( -1,-2).
22.(1)证明:∵AB=AC,∴∠B=∠C.
在△BDE 和△CEF中,
∴DE=EF.∴△DEF 是等腰三角形.
(2)解:∵∠DEC=∠B+∠BDE,∠DEC=∠DEF+∠CEF,∴∠DEF+∠CEF=∠B+∠BDE.
∵△BDE≌△CEF,∴∠CEF=∠BDE.∴∠DEF=∠B.
又∵在△ABC中,AB=AC,∠A=50°,∴∠B=65°.∴∠DEF=65°.
(3)解:由(1)知,△DEF是等腰三角形,即DE=EF.
由(2)知,∠DEF=∠B.
∵∠A=∠DEF,∴∠A=∠B.∵AB=AC,∴∠B=∠C.
∴∠A=∠B=∠C.∴△ABC是等边三角形.
∴∠B=∠DEF=60°.∴△DEF是等边三角形.
23.(1)解:∵∠B=α,∠A=2∠B,∴∠A=2α.
∴∠ACB=180°-(∠A+∠B) =180°-3α.
∵ CE平分.
∵ CD是△ABC的高,∴∠ADC=90°.∴∠ACD=90°-∠A=90°-2α.
x
(2)证明:在 DA 上截取DM=DE,连接CM,如图.
α.
∴∠BMC=∠BCM.∴BC=BM.∴BM=BE+ME=BE+2DE.
∴BC=BE+2DE.∴BC-BE=2DE.
(3)解:∵△BCE沿直线 BC折叠得到△BCF,∴△BCE≌△BCF.
∴BE=BF,CE=CF,∠EBC=∠FBC,∠ECB=∠FCB.
∵CF∥AB,∴∠FCB=∠EBC.
∴∠FCB=∠FBC=∠ECB=∠EBC.∴CF=BF=BE=EC.
∴∠EBC=∠ECB=∠ACE=α.∴∠ACB=∠CAB=2α.
∴在△ABC中,2α+2α+α=180°.∴α=36°.∴∠DCE= α=18°.
