沪科版数学八年级上册 期末检测卷(含答案)
文档属性
| 名称 | 沪科版数学八年级上册 期末检测卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 906.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-07 14:58:36 | ||
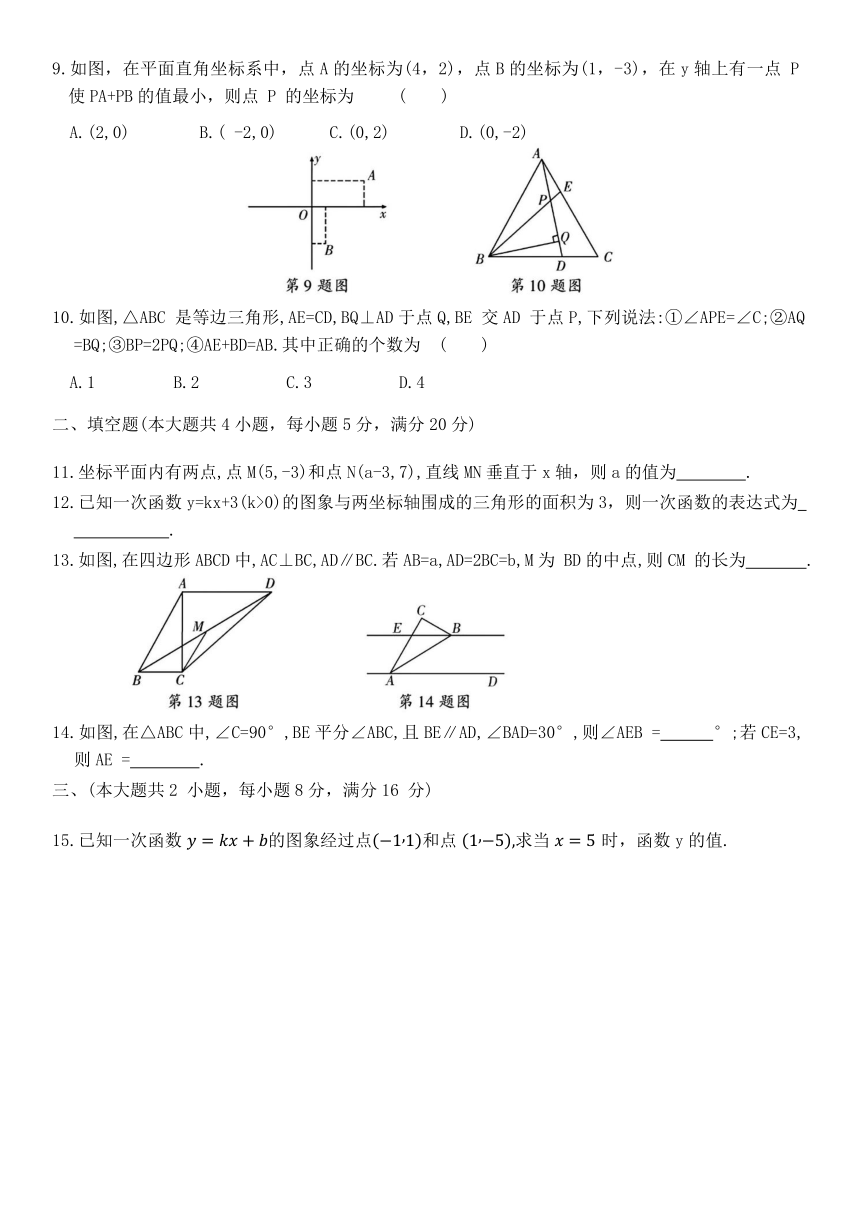
图片预览



文档简介
期末检测卷
(时间:120分钟 满分:150分)
题 号 一 二 三 四 五 六 七 八 总分
得 分
一、选择题(本大题共10 小题,每小题4分,满分40 分)
1.已知平面直角坐标系有一点P(x,x+2),无论x取何值,点P不可能在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.下列图形中,对称轴最多的图形是 ( )
3.已知点M(1,a),N(-2,b)是一次函数y= -2x+1图象上的两点,则a与b的大小关系是 ( )
A. a>b B. a=b C. a4.为了估计池塘岸边A,B 两点之间的距离,小明在池塘的一侧选取一点C,测得AC=3m,BC=6m,则A,B两点之间的距离可能是 ( )
A.11m B.9 m C.7 m D. 3m
5.下列命题中是假命题的是 ( )
A.全等三角形的对应角相等
B.三角形的外角大于任何一个内角
C.等边对等角
D.角平分线上的点到角两边的距离相等
6.如图,∠ABD=∠CBD,现添加以下条件不能判定△ABD≌△CBD的是( )
A.∠A=∠C B.∠BDA=∠BDC
C. AB=CB D. AD=CD
7.如图,在Rt△ABC中,∠C=90°,∠B=30°,AD 是∠BAC 的角平分线,AD=2,则点 D 到线段AB的距离为 ( )
B.1 C.2 D.4
8.若ab<0且a9.如图,在平面直角坐标系中,点A的坐标为(4,2),点B的坐标为(1,-3),在y轴上有一点 P 使PA+PB的值最小,则点 P 的坐标为 ( )
A.(2,0) B.( -2,0) C.(0,2) D.(0,-2)
10.如图,△ABC 是等边三角形,AE=CD,BQ⊥AD于点Q,BE 交AD 于点P,下列说法:①∠APE=∠C;②AQ=BQ;③BP=2PQ;④AE+BD=AB.其中正确的个数为 ( )
A.1 B.2 C.3 D.4
二、填空题(本大题共4小题,每小题5分,满分20分)
11.坐标平面内有两点,点M(5,-3)和点N(a-3,7),直线MN垂直于x轴,则a的值为 .
12.已知一次函数y=kx+3(k>0)的图象与两坐标轴围成的三角形的面积为3,则一次函数的表达式为 .
13.如图,在四边形ABCD中,AC⊥BC,AD∥BC.若AB=a,AD=2BC=b,M为 BD的中点,则CM 的长为 .
14.如图,在△ABC中,∠C=90°,BE平分∠ABC,且BE∥AD,∠BAD=30°,则∠AEB = °;若CE=3,则AE = .
三、(本大题共2 小题,每小题8分,满分16 分)
15.已知一次函数 的图象经过点和点 求当 时,函数y的值.
的三个顶点的坐标分别为
(1)在所给的平面直角坐标系中画出.
(2)以y轴为对称轴,作 的轴对称图形. ,并写出点. 的坐标.
四、(本大题共2 小题,每小题8分,满分16 分)
17.如图,在平面直角坐标系中,点A,B,C的坐标分别为(0,3),(3,3),(3,0).正方形OABC从图中的位置出发,以每秒旋转 的速度,绕点 O 沿顺时针方向旋转.同时,点 P 从点 O 出发,以每秒移动1 个单位的速度,沿正方形的边,按照O→A→B→C→O→A…的路线循环运动.
(1)第1秒时点 P 的坐标为(1,0),写出第2 秒时点 P 的坐标;
(2)写出第2 021 秒时点 P 的坐标.
18.如图,在等腰. 和等腰 中, 且C,E,D三点共线,作 于点 M,求证:
五、(本大题共2 小题,每小题10分,满分20 分)
19.某童装店以每件25 元的价格购进某种品牌的童装若干件,销售了部分童装后,剩下的童装每件降价10元销售,全部售完.销售总额y(元)与销售量x(件)之间的关系如图所示,请根据图象提供的信息完成下列问题:
(1)求降价后销售总额y(元)与销售量x(件)之间的函数表达式,并写出自变量的取值范围;
(2)求该童装店这次销售童装盈利多少元
20.如图,在 中, ,BP,CP分别是 和 的平分线,且
(1)求 的周长;
(2)若 求 的度数.
六、(本题满分12 分)
21.小明进行市场调查后计划购进甲、乙商品共100件进行销售,设小明购进甲商品x件,甲、乙商品全部销售完后获得利润为y元.
甲商品 乙商品
进价/(元/件) 65 5
售价/(元/件) 90 10
(1)求出y与x之间的函数表达式;
(2)小明用不超过3 500 元资金一次性购进甲、乙两种商品,求x的取值范围;
(3)在(2)的条件下,若要求甲、乙商品全部销售完后获得的利润不少于1 450元,请说明小明有哪些可行的进货方案,并计算哪种进货方案的利润最大,最大利润是多少
七、(本题满分12分)
22.如图,在平面直角坐标系中,过点 C(0,6)的直线 AC 与直线 OA 相交于点A(4,2).
(1)求直线AC 的表达式;
(2)求 的面积;
(3)动点M在线段OA 和射线AC 上运动,是否存在点M,使 的面积是△OAC的面积的 若存在,求出此时点 M 的坐标;若不存在,请说明理由.
八、(本题满分14分)
23.数学模型学习与应用.
(1)【学习】如图1,∠BAD=90°,AB=AD,BC⊥AC于点C,DE⊥AC于点E.由∠1+∠2=∠2+∠D=90°,得∠1=∠D;又∠ACB=∠AED=90°,可以通过推理得到△ABC≌△DAE,进而得到AC= ,BC= ;
(2)【应用】如图2,在△ABC中,AB=AC,点D,A,E都在直线l上,并且∠BDA=∠AEC=∠BAC=α.若DE=a,BD=b,求CE的长度(用含a,b的代数式表示);
(3)【拓展】如图3,在(2)的条件下,若α=120°,且△ACF 是等边三角形,试判断△DEF的形状,并说明理由.
期末检测卷
1. D 2. D 3. C 4. C 5. B 6. D 7. B 8. B 9. D 10. C 11.812. y= x+3 13. 14.120 6
15.解:∵一次函数y=kx+b的图象经过点( -1,1)和点(1,-5), 解得 .一次函数的表达式为y=-3x-2.把x=5代入y= -3x-2,得y= -3×5-2= -17.
∴当x=5时,函数y的值为-17.
16.解:(1)如图,△ABC即为所求.
(2)如图,△A'B'C'即为所求.点 B'的坐标为( -4,-3).
17.解:(1)第2秒时,点P在OA上,OP=2,此时OA 在y轴的负半轴上,∴第2秒时点 P 的坐标为P(0,-2).
(2)正方形每4秒一个循环,2021÷4=505……1.∴2021秒时,点B 在第四象限.
∵2 021÷12=168……5,∴第2021秒时点 P在AB上,点P的坐标为(3,-2).
18.证明:∵∠BAC=∠DAE,∴∠BAD+∠EAB=∠CAE+∠EAB.∴∠BAD=∠CAE.在△AEC 和△ADB中,(CABS∠BAD,∴△AEC≌△ADB(SAS).∴BD=∠CE.
∵AD=AE,AM⊥CD,∴DM=EM.∴BD+DM=CE+EM=CM.
19.解:(1)设降价后销售金额y(元)与销售量x(件)之间的函数关系式是y=kx+b.根据题意,得该函数过点(40,1 800),(55,2 325).
则 解得∴y=35x+400(40∴降价后销售总额y(元)与销售量x(件)之间的函数关系式是y=35x+400,自变量的取值范围是40(2)2325-25×55=950(元).
∴该童装店这次销售童装盈利950元.
20.解:(1)∵ BP,CP分别是∠ABC 和∠ACB的平分线,
∴∠ABP=∠PBD,∠ACP=∠PCE.
∵ PD∥AB,PE∥AC,∴∠ABP=∠BPD,∠ACP=∠CPE.
∴∠PBD=∠BPD,∠PCE=∠CPE.∴BD=PD,CE=PE.
∴△PDE的周长=PD+DE+PE=BD+DE+EC=BC=8cm.
∵ BP,CP 分别是∠ABC 和∠ACB的平分线,
21.解:(1)根据题意,得y=(90-65)x+(10-5)(100-x)=20x+500.
(2)根据题意,得65x+5(100-x)≤3 500.解得x≤50.
又∵x≥0,∴x的取值范围是0≤x≤50.
(3)根据题意,得20x+500≥1 450.解得x≥47.5.∴47.5≤x≤50.
又∵x为整数,∴x=48,49,50;
∴进货方案有:甲商品进48件,乙商品进52件;甲商品进49件,乙商品进51件;甲商品进50件,乙商品进50件.
∵y=20x+500,∴y随x的增大而增大.
∴当x=50时,有最大利润. y最大=20×50+500=1500(元).
∴当甲商品进50件,乙商品进50件时,利润最大.利润最大为1500元.
22.解:(1)设直线AC的表达式为y=kx+b.
根据题意,得 解得
∴ 直线AC的表达式为y= -x+6.
(2)∵C(0,6),A(4,2),∴
(3)存在.设直线OA的表达式为y=mx.则4m=2.解得
∴ 直线 OA 的表达式为
∵△OMC的面积是△OAC的面积的
∴点M的横坐标为2 或-2.
当点 M的横坐标为2时,
将x=2代入 中,得y=1,则点M的坐标为(2,1);
将x=2代入y=-x+6中,得y=4,则点M的坐标为(2,4).
当点 M的横坐标为-2时,
将x=-2代入y=-x+6中,得y=8,则点M 的坐标为( -2,8).
综上所述,点M的坐标为(2,1)或(2,4)或( -2,8).
23.解:(1)DE AE
(2)∵∠BDA=∠BAC=α,∴∠DBA+∠BAD=180°-α=∠BAD+∠CAE.
∴∠CAE=∠ABD.
在△ABD和△CAE 中,
∴AD=CE,BD=AE.∴DE=AD+AE=CE+BD.
∵ DE=a,BD=b,∴CE=DE-BD=a-b.
(3)△DEF是等边三角形.理由如下:
由(2)知,△ABD≌△CAE,∴BD=AE,∠ABD=∠CAE.
∵△ACF是等边三角形,∴∠CAF=60°,AC=AF.
∵AB=AC,∠BAC=120°,∴AB=AF,∠BAF=60°.∴△ABF是等边三角形.
∴FB=FA,∠BFA=60°,∠ABD+∠ABF=∠CAE+∠CAF,即∠FBD=∠FAE.
在△BDF 和△AEF中,
∴△BDF≌△AEF(SAS).∴DF=EF,∠BFD=∠AFE.
∴∠DFE=∠AFD+∠AFE=∠AFD+∠BFD=∠BFA=60°.
∴△DEF 是等边三角形.
(时间:120分钟 满分:150分)
题 号 一 二 三 四 五 六 七 八 总分
得 分
一、选择题(本大题共10 小题,每小题4分,满分40 分)
1.已知平面直角坐标系有一点P(x,x+2),无论x取何值,点P不可能在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.下列图形中,对称轴最多的图形是 ( )
3.已知点M(1,a),N(-2,b)是一次函数y= -2x+1图象上的两点,则a与b的大小关系是 ( )
A. a>b B. a=b C. a4.为了估计池塘岸边A,B 两点之间的距离,小明在池塘的一侧选取一点C,测得AC=3m,BC=6m,则A,B两点之间的距离可能是 ( )
A.11m B.9 m C.7 m D. 3m
5.下列命题中是假命题的是 ( )
A.全等三角形的对应角相等
B.三角形的外角大于任何一个内角
C.等边对等角
D.角平分线上的点到角两边的距离相等
6.如图,∠ABD=∠CBD,现添加以下条件不能判定△ABD≌△CBD的是( )
A.∠A=∠C B.∠BDA=∠BDC
C. AB=CB D. AD=CD
7.如图,在Rt△ABC中,∠C=90°,∠B=30°,AD 是∠BAC 的角平分线,AD=2,则点 D 到线段AB的距离为 ( )
B.1 C.2 D.4
8.若ab<0且a
A.(2,0) B.( -2,0) C.(0,2) D.(0,-2)
10.如图,△ABC 是等边三角形,AE=CD,BQ⊥AD于点Q,BE 交AD 于点P,下列说法:①∠APE=∠C;②AQ=BQ;③BP=2PQ;④AE+BD=AB.其中正确的个数为 ( )
A.1 B.2 C.3 D.4
二、填空题(本大题共4小题,每小题5分,满分20分)
11.坐标平面内有两点,点M(5,-3)和点N(a-3,7),直线MN垂直于x轴,则a的值为 .
12.已知一次函数y=kx+3(k>0)的图象与两坐标轴围成的三角形的面积为3,则一次函数的表达式为 .
13.如图,在四边形ABCD中,AC⊥BC,AD∥BC.若AB=a,AD=2BC=b,M为 BD的中点,则CM 的长为 .
14.如图,在△ABC中,∠C=90°,BE平分∠ABC,且BE∥AD,∠BAD=30°,则∠AEB = °;若CE=3,则AE = .
三、(本大题共2 小题,每小题8分,满分16 分)
15.已知一次函数 的图象经过点和点 求当 时,函数y的值.
的三个顶点的坐标分别为
(1)在所给的平面直角坐标系中画出.
(2)以y轴为对称轴,作 的轴对称图形. ,并写出点. 的坐标.
四、(本大题共2 小题,每小题8分,满分16 分)
17.如图,在平面直角坐标系中,点A,B,C的坐标分别为(0,3),(3,3),(3,0).正方形OABC从图中的位置出发,以每秒旋转 的速度,绕点 O 沿顺时针方向旋转.同时,点 P 从点 O 出发,以每秒移动1 个单位的速度,沿正方形的边,按照O→A→B→C→O→A…的路线循环运动.
(1)第1秒时点 P 的坐标为(1,0),写出第2 秒时点 P 的坐标;
(2)写出第2 021 秒时点 P 的坐标.
18.如图,在等腰. 和等腰 中, 且C,E,D三点共线,作 于点 M,求证:
五、(本大题共2 小题,每小题10分,满分20 分)
19.某童装店以每件25 元的价格购进某种品牌的童装若干件,销售了部分童装后,剩下的童装每件降价10元销售,全部售完.销售总额y(元)与销售量x(件)之间的关系如图所示,请根据图象提供的信息完成下列问题:
(1)求降价后销售总额y(元)与销售量x(件)之间的函数表达式,并写出自变量的取值范围;
(2)求该童装店这次销售童装盈利多少元
20.如图,在 中, ,BP,CP分别是 和 的平分线,且
(1)求 的周长;
(2)若 求 的度数.
六、(本题满分12 分)
21.小明进行市场调查后计划购进甲、乙商品共100件进行销售,设小明购进甲商品x件,甲、乙商品全部销售完后获得利润为y元.
甲商品 乙商品
进价/(元/件) 65 5
售价/(元/件) 90 10
(1)求出y与x之间的函数表达式;
(2)小明用不超过3 500 元资金一次性购进甲、乙两种商品,求x的取值范围;
(3)在(2)的条件下,若要求甲、乙商品全部销售完后获得的利润不少于1 450元,请说明小明有哪些可行的进货方案,并计算哪种进货方案的利润最大,最大利润是多少
七、(本题满分12分)
22.如图,在平面直角坐标系中,过点 C(0,6)的直线 AC 与直线 OA 相交于点A(4,2).
(1)求直线AC 的表达式;
(2)求 的面积;
(3)动点M在线段OA 和射线AC 上运动,是否存在点M,使 的面积是△OAC的面积的 若存在,求出此时点 M 的坐标;若不存在,请说明理由.
八、(本题满分14分)
23.数学模型学习与应用.
(1)【学习】如图1,∠BAD=90°,AB=AD,BC⊥AC于点C,DE⊥AC于点E.由∠1+∠2=∠2+∠D=90°,得∠1=∠D;又∠ACB=∠AED=90°,可以通过推理得到△ABC≌△DAE,进而得到AC= ,BC= ;
(2)【应用】如图2,在△ABC中,AB=AC,点D,A,E都在直线l上,并且∠BDA=∠AEC=∠BAC=α.若DE=a,BD=b,求CE的长度(用含a,b的代数式表示);
(3)【拓展】如图3,在(2)的条件下,若α=120°,且△ACF 是等边三角形,试判断△DEF的形状,并说明理由.
期末检测卷
1. D 2. D 3. C 4. C 5. B 6. D 7. B 8. B 9. D 10. C 11.812. y= x+3 13. 14.120 6
15.解:∵一次函数y=kx+b的图象经过点( -1,1)和点(1,-5), 解得 .一次函数的表达式为y=-3x-2.把x=5代入y= -3x-2,得y= -3×5-2= -17.
∴当x=5时,函数y的值为-17.
16.解:(1)如图,△ABC即为所求.
(2)如图,△A'B'C'即为所求.点 B'的坐标为( -4,-3).
17.解:(1)第2秒时,点P在OA上,OP=2,此时OA 在y轴的负半轴上,∴第2秒时点 P 的坐标为P(0,-2).
(2)正方形每4秒一个循环,2021÷4=505……1.∴2021秒时,点B 在第四象限.
∵2 021÷12=168……5,∴第2021秒时点 P在AB上,点P的坐标为(3,-2).
18.证明:∵∠BAC=∠DAE,∴∠BAD+∠EAB=∠CAE+∠EAB.∴∠BAD=∠CAE.在△AEC 和△ADB中,(CABS∠BAD,∴△AEC≌△ADB(SAS).∴BD=∠CE.
∵AD=AE,AM⊥CD,∴DM=EM.∴BD+DM=CE+EM=CM.
19.解:(1)设降价后销售金额y(元)与销售量x(件)之间的函数关系式是y=kx+b.根据题意,得该函数过点(40,1 800),(55,2 325).
则 解得∴y=35x+400(40
∴该童装店这次销售童装盈利950元.
20.解:(1)∵ BP,CP分别是∠ABC 和∠ACB的平分线,
∴∠ABP=∠PBD,∠ACP=∠PCE.
∵ PD∥AB,PE∥AC,∴∠ABP=∠BPD,∠ACP=∠CPE.
∴∠PBD=∠BPD,∠PCE=∠CPE.∴BD=PD,CE=PE.
∴△PDE的周长=PD+DE+PE=BD+DE+EC=BC=8cm.
∵ BP,CP 分别是∠ABC 和∠ACB的平分线,
21.解:(1)根据题意,得y=(90-65)x+(10-5)(100-x)=20x+500.
(2)根据题意,得65x+5(100-x)≤3 500.解得x≤50.
又∵x≥0,∴x的取值范围是0≤x≤50.
(3)根据题意,得20x+500≥1 450.解得x≥47.5.∴47.5≤x≤50.
又∵x为整数,∴x=48,49,50;
∴进货方案有:甲商品进48件,乙商品进52件;甲商品进49件,乙商品进51件;甲商品进50件,乙商品进50件.
∵y=20x+500,∴y随x的增大而增大.
∴当x=50时,有最大利润. y最大=20×50+500=1500(元).
∴当甲商品进50件,乙商品进50件时,利润最大.利润最大为1500元.
22.解:(1)设直线AC的表达式为y=kx+b.
根据题意,得 解得
∴ 直线AC的表达式为y= -x+6.
(2)∵C(0,6),A(4,2),∴
(3)存在.设直线OA的表达式为y=mx.则4m=2.解得
∴ 直线 OA 的表达式为
∵△OMC的面积是△OAC的面积的
∴点M的横坐标为2 或-2.
当点 M的横坐标为2时,
将x=2代入 中,得y=1,则点M的坐标为(2,1);
将x=2代入y=-x+6中,得y=4,则点M的坐标为(2,4).
当点 M的横坐标为-2时,
将x=-2代入y=-x+6中,得y=8,则点M 的坐标为( -2,8).
综上所述,点M的坐标为(2,1)或(2,4)或( -2,8).
23.解:(1)DE AE
(2)∵∠BDA=∠BAC=α,∴∠DBA+∠BAD=180°-α=∠BAD+∠CAE.
∴∠CAE=∠ABD.
在△ABD和△CAE 中,
∴AD=CE,BD=AE.∴DE=AD+AE=CE+BD.
∵ DE=a,BD=b,∴CE=DE-BD=a-b.
(3)△DEF是等边三角形.理由如下:
由(2)知,△ABD≌△CAE,∴BD=AE,∠ABD=∠CAE.
∵△ACF是等边三角形,∴∠CAF=60°,AC=AF.
∵AB=AC,∠BAC=120°,∴AB=AF,∠BAF=60°.∴△ABF是等边三角形.
∴FB=FA,∠BFA=60°,∠ABD+∠ABF=∠CAE+∠CAF,即∠FBD=∠FAE.
在△BDF 和△AEF中,
∴△BDF≌△AEF(SAS).∴DF=EF,∠BFD=∠AFE.
∴∠DFE=∠AFD+∠AFE=∠AFD+∠BFD=∠BFA=60°.
∴△DEF 是等边三角形.
同课章节目录
