沪科版数学八年级上册期末综合检测卷(含答案)
文档属性
| 名称 | 沪科版数学八年级上册期末综合检测卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 991.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-07 15:00:46 | ||
图片预览


文档简介
期末综合检测卷
(时间:120分钟满分:150分)
题 号 一 二 三 四 五 六 七 八 总分
得 分
一、选择题(本大题共10 小题,每小题4分,满分40 分)
1.在平面直角坐标系中,点P(2,-3)关于y轴对称的点的坐标是 ( )
A.( -2,-3) B.(-2,3) C.(2,3) D.(2,-3)
2.下列四个函数中,y随x的增大而减小的是 ( )
A. y=3x B. y=1+2x
C. y=1-2x D. y= -1+x
3.下列命题中正确的是 ( )
A.等腰三角形的角平分线、中线、高线互相重合
B.在角的内部,到角两边距离相等的点在这个角的平分线上
C.有一个角是60°的三角形是等边三角形
D.有两边及一边的对角对应相等的两个三角形全等
4.已知点P(a,3+a)在第二象限,则a的取值范围是 ( )
A. a<0 B. a> -3
C. -35.下列条件中,不能确定△ABC的形状和大小的是 ( )
A. AB=5,BC=6,AC=7 B. AB=5,BC=6,∠B=45°
C. AB=5,AC=4,∠B=45° D. AB=5,AC=4,∠C=90°
6.设三角形三边之长分别为3,8,1-2a,则a的取值范围为 ( )
A.3C. -22
7.如图,△ABC≌△ADE,若∠B=75°,∠C=28°,∠DAC=30°,则∠BAE的度数为 ( )
A.45° B.47° C.110° D.124°
8.如图,P 是 的三条角平分线的交点,连接PA,PB,PC,若 的面积分别为 则 ( )
D.无法确定 与 的大小
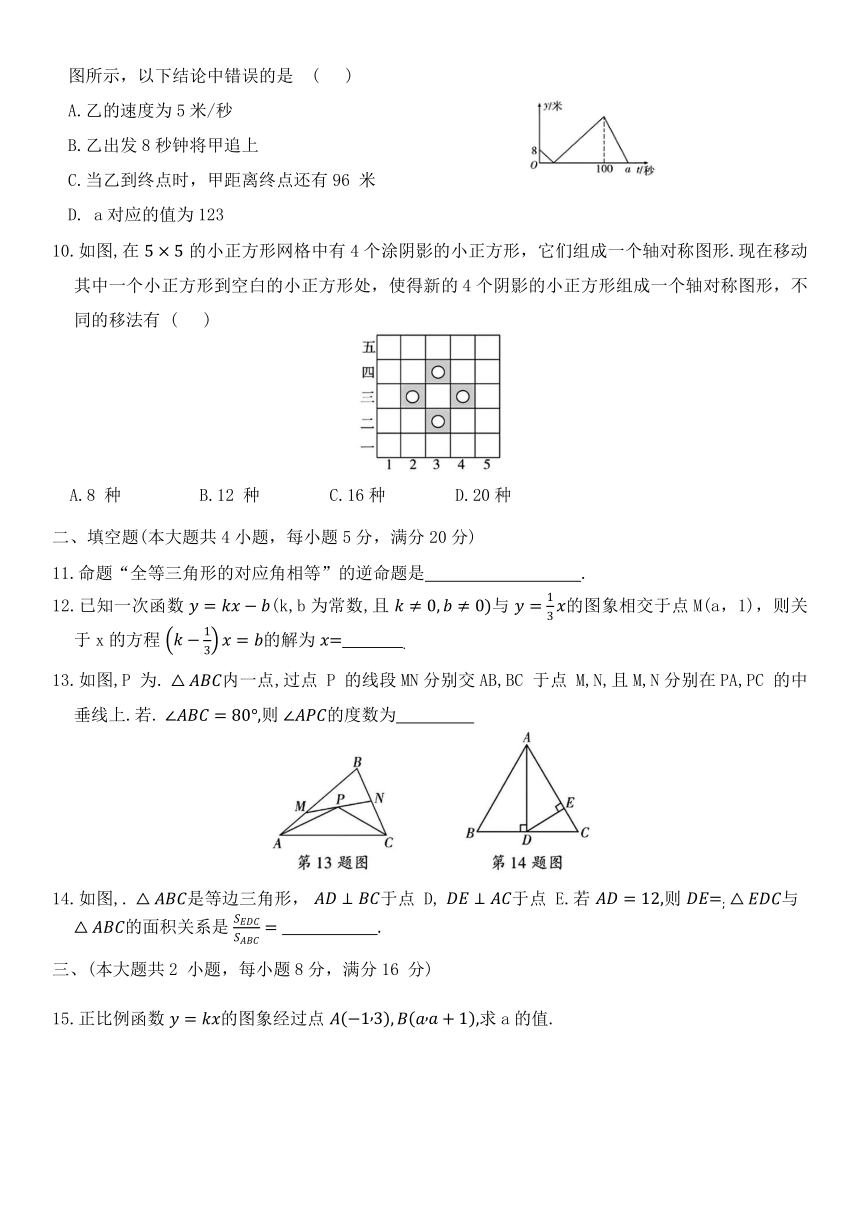
9.甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步500米,先到终点的人原地休息.已知甲先出发2秒,在跑步过程中,甲、乙两人之间的距离y(米)与乙出发的时间t(秒)之间的关系如图所示,以下结论中错误的是 ( )
A.乙的速度为5米/秒
B.乙出发8秒钟将甲追上
C.当乙到终点时,甲距离终点还有96 米
D. a对应的值为123
10.如图,在 的小正方形网格中有4个涂阴影的小正方形,它们组成一个轴对称图形.现在移动其中一个小正方形到空白的小正方形处,使得新的4个阴影的小正方形组成一个轴对称图形,不同的移法有 ( )
A.8 种 B.12 种 C.16种 D.20种
二、填空题(本大题共4小题,每小题5分,满分20分)
11.命题“全等三角形的对应角相等”的逆命题是 .
12.已知一次函数 (k,b为常数,且 与 的图象相交于点M(a,1),则关于x的方程 的解为
13.如图,P 为. 内一点,过点 P 的线段MN分别交AB,BC 于点 M,N,且M,N分别在PA,PC 的中垂线上.若. 则 的度数为
14.如图,. 是等边三角形, 于点 D, 于点 E.若 则 与 的面积关系是
三、(本大题共2 小题,每小题8分,满分16 分)
15.正比例函数 的图象经过点 求a的值.
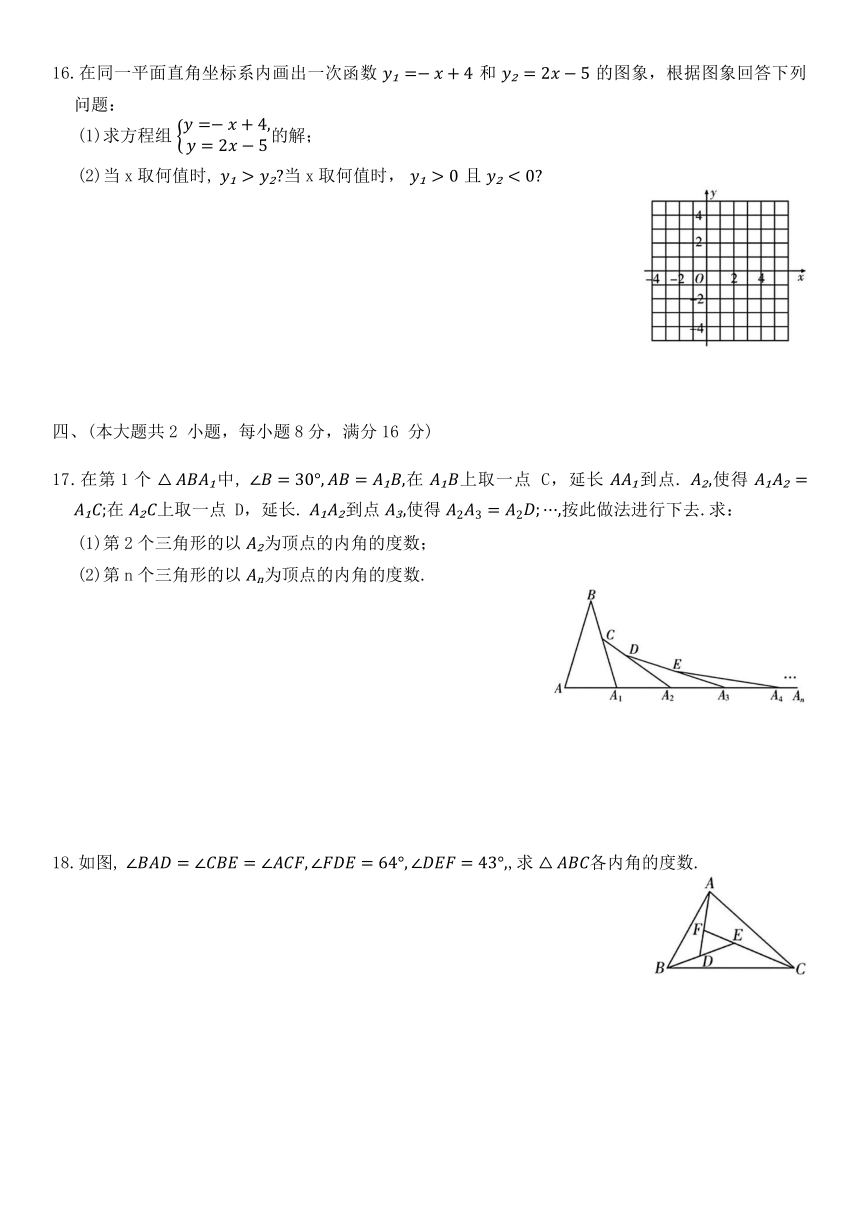
16.在同一平面直角坐标系内画出一次函数 和 的图象,根据图象回答下列问题:
(1)求方程组 的解;
(2)当x取何值时, 当x取何值时, 且
四、(本大题共2 小题,每小题8分,满分16 分)
17.在第1个 中, 在 上取一点 C,延长 到点. 使得 在 上取一点 D,延长. 到点 使得 按此做法进行下去.求:
(1)第2个三角形的以 为顶点的内角的度数;
(2)第n个三角形的以 为顶点的内角的度数.
18.如图, ,求 各内角的度数.
五、(本大题共2 小题,每小题10 分,满分20 分)
19.某农产品店利用网络将优质土特产销往全国,其中销售的核桃和花生这两种商品的相关信息如下表.根据下表提供的信息,解答下列问题:
商品 核桃 花生
规格 1 kg/袋 2 kg/袋
利润 10元/袋 8元/袋
(1)已知今年上半年,该店销售上表规格的核桃和花生共3 000kg,获得利润21 000 元,求上半年该店销售这种规格的核桃和花生各多少袋
(2)根据之前的销售情况,估计今年下半年该店还能销售上表规格的核桃和花生共2 000kg,其中,核桃的销售量不低于600 kg.假设今年下半年,销售上表规格的核桃为x(kg),销售上表规格的核桃和花生获得的总利润为 W(元),写出W与x之间的函数表达式,并求下半年该店销售这种规格的核桃和花生至少获得的总利润.
20.如图,在 中,点E,F 分别在AB,AC 上,AD 是EF的垂直平分线, EF 交 AD 于点 G.
(1)求证:AD平分.
(2)若 求证:
六、(本题满分12 分)
21.工厂某车间需加工一批零件,甲组工人加工中因故停产检修机器一次,然后以原来的工作效率继续加工,由于时间紧任务重,乙组工人也加入共同加工零件.设甲组加工时间为t(时),甲组加工零件的数量为y甲(个),乙组加工零件的数量为yz(个),其函数图象如图所示.
(1)求yz 与t之间的函数表达式,并写出t的取值范围;
(2)求a的值,并说明a的实际意义;
(3)甲组加工多长时间时,甲、乙两组加工零件的总数为480 个.
七、(本题满分12 分)
22.如图,在平面直角坐标系中,直线 与x轴交于点A,与y轴交于点B,已知 ,点 P 是第一象限内在直线AB 上一点.
(1)直接写出k,b的值;
(2)设P(x,y),求 的面积S与x的函数表达式;
(3)当 时,求点 P 的坐标.
八、(本题满分14分)
23.如图1,在 中, 点D 是线段CA 延长线上一点,且. AB,点 F 是线段AB上一点,连接DF,以DF 为斜边作等腰 连接 EA,EA 满足条件
(1)若 ,求AB的长度;
(2)求证:
(3)如图2,点 F 是线段BA 延长线上一点,探究 AE,AF,BC 之间的数量关系,并证明你的结论.
期末综合检测卷
1. A 2. C 3. B 4. C 5. C 6. B 7. D 8. A 9. C 10. D
11.对应角相等的三角形是全等三角形 12.3 13.130°14.6
15.解:∵正比例函数y=kx的图象经过点.A(-1,3),B(a,a+1), 解得 ∴a的值为
16.解:画出一次函数 和 的图象如图.
(1)∵一次函数 和 的图象相交于点(3,1),∴ 方程组 的解为
(2)由图可知,当x<3时,y >y ;当x<2.5时,,y >0且
17.解:(1)∵在△ABA 中,
1是△A A C的外角,∴
(2)同(1)可得 ∴第n个三角形的以An为顶角的内角
18.解:∵∠FDE=∠BAD+∠ABD,∠BAD=∠CBE,∠FDE=64°,∴∠FDE=∠ABD+∠CBE=∠ABC.∴∠ABC=64°.
同理可得,∠DEF=∠FCB+∠CBE=∠FCB+∠ACF=∠ACB.又∵∠DEF=43°,∴∠ACB=43°.∴∠BAC=180°-∠ABC-∠ACB=180°-64°-43°=73°.
∴△ABC各内角的度数分别为64°,43°,73°.
19.解:(1)设今年上半年农产品店销售这种规格的核桃mkg,花生(3 000-m) kg.根据题意,得 解得m=1 500.
(袋).
答:今年上半年农产品店销售这种规格的核桃1 500袋和花生750 袋.
(2)根据题意,得
∵600≤x<2000,且6>0,∴W随x的增大而增大.
∴当x=600时,W有最小值, (元).
答:下半年该农产品店销售这种规格的核桃和花生至少获得的总利润为11 600 元.
20.证明:(1)∵AD 是EF的垂直平分线,∴DE=DF.
∵DE⊥AB,DF⊥AC,∴AD平分∠BAC.
(2)∵∠BAC=60°,AD平分
∵DE⊥AB,DF⊥AC,AD⊥EF,∴∠EAD+∠AEG=∠DEG+∠AEG=90°.
∴∠DEG=∠EAD=30°.∴DE=2DG.
21.解:(1)设yz与t之间的函数表达式是
根据题意,得yz 的图象过点(5,0)和(8,360),代入 得 解得
∴yz与t之间的函数表达式是:
(2)由图象可得,甲的工作效率为120÷3=40(个/时).
a=120+40×(8-4)=280,即a的值是280.
实际意义是当甲加工8小时时,一共加工了280个零件.
(3)设甲组加工c小时时,甲、乙两组加工零件的总数为480 个.根据题意,得120+40(c-4)+(120c-600)=480.解得c=7.即甲组加工7小时时,甲、乙两组加工零件的总数为480个.
22.解:(1)k= -1,b=6.
(2)如图,过点P作PH⊥OA于点H.
∵点P(x,y)是第一象限内在直线y=-x+6上一点,
∴PH= -x+6(0∴△OPA的面积S关于x的函数表达式为y=-3x+18(0(3)∵OA=OB,∠AOB=90°,∴∠OAB=∠OBA=45°.
又∵PH⊥OA,OA=6,OP=AP,
∴OH=HA=3,∠HPA=∠PAH=45°.∴AH=PH=3.∴点P的坐标为(3,3).
23.(1)解:如图1,∵在等腰直角三角形DEF 中,∠DEF=90°,∠1=20°,
∴∠2=∠DEF--∠1=70°.
∵∠ADE+∠2+∠3=180°,∠ADE=50°,∴∠3=60°.
∵EA⊥AB,∴∠EAB=90°.∵∠3+∠EAB+∠4=180°,∴∠4=30°.
∵∠C=90°,∴AB=2BC=4.
(2)证明:如图1,过点 D作DM⊥AE于点M,在△DEM中,∠2+∠5=90°.
∵∠2 +∠1=90°,∴∠1 =∠5.
在△DEM 和△EFA中,(200°,∴△DEM≌△EFA(AAS).∴AF=ME.
∵∠3+∠EAB+∠4=180°,∠EAB=90°,∴∠3+∠4=90°.
∵∠C=90°,∴∠4+∠B=90°.∴∠3=∠B.
在△DAM 和△ABC中
∴BC=AM.∴AE=ME+AM=AF+BC.
(3)解:AE+AF=BC.证明如下:
如图2,过点 D作DM⊥AE交AE的延长线于点 M.
∵∠C=90°,∴∠1 +∠B=90°.
∵∠2+∠MAB+∠1=180°,∠MAB=90°,∴∠2+∠1=90°.∴∠2=∠B.
在△ADM 和△BAC中,
∵∠3+∠DEF+∠4=180°,∠DEF=90°,∴∠3 +∠4=90°.
∵∠M=90°,∴∠3+∠5 =90°.∴∠4=∠5.
在△MED 和△AFE中,
∴AE+AF=AE+ME=AM=BC,即AE+AF=BC.
(时间:120分钟满分:150分)
题 号 一 二 三 四 五 六 七 八 总分
得 分
一、选择题(本大题共10 小题,每小题4分,满分40 分)
1.在平面直角坐标系中,点P(2,-3)关于y轴对称的点的坐标是 ( )
A.( -2,-3) B.(-2,3) C.(2,3) D.(2,-3)
2.下列四个函数中,y随x的增大而减小的是 ( )
A. y=3x B. y=1+2x
C. y=1-2x D. y= -1+x
3.下列命题中正确的是 ( )
A.等腰三角形的角平分线、中线、高线互相重合
B.在角的内部,到角两边距离相等的点在这个角的平分线上
C.有一个角是60°的三角形是等边三角形
D.有两边及一边的对角对应相等的两个三角形全等
4.已知点P(a,3+a)在第二象限,则a的取值范围是 ( )
A. a<0 B. a> -3
C. -3
A. AB=5,BC=6,AC=7 B. AB=5,BC=6,∠B=45°
C. AB=5,AC=4,∠B=45° D. AB=5,AC=4,∠C=90°
6.设三角形三边之长分别为3,8,1-2a,则a的取值范围为 ( )
A.3
7.如图,△ABC≌△ADE,若∠B=75°,∠C=28°,∠DAC=30°,则∠BAE的度数为 ( )
A.45° B.47° C.110° D.124°
8.如图,P 是 的三条角平分线的交点,连接PA,PB,PC,若 的面积分别为 则 ( )
D.无法确定 与 的大小
9.甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步500米,先到终点的人原地休息.已知甲先出发2秒,在跑步过程中,甲、乙两人之间的距离y(米)与乙出发的时间t(秒)之间的关系如图所示,以下结论中错误的是 ( )
A.乙的速度为5米/秒
B.乙出发8秒钟将甲追上
C.当乙到终点时,甲距离终点还有96 米
D. a对应的值为123
10.如图,在 的小正方形网格中有4个涂阴影的小正方形,它们组成一个轴对称图形.现在移动其中一个小正方形到空白的小正方形处,使得新的4个阴影的小正方形组成一个轴对称图形,不同的移法有 ( )
A.8 种 B.12 种 C.16种 D.20种
二、填空题(本大题共4小题,每小题5分,满分20分)
11.命题“全等三角形的对应角相等”的逆命题是 .
12.已知一次函数 (k,b为常数,且 与 的图象相交于点M(a,1),则关于x的方程 的解为
13.如图,P 为. 内一点,过点 P 的线段MN分别交AB,BC 于点 M,N,且M,N分别在PA,PC 的中垂线上.若. 则 的度数为
14.如图,. 是等边三角形, 于点 D, 于点 E.若 则 与 的面积关系是
三、(本大题共2 小题,每小题8分,满分16 分)
15.正比例函数 的图象经过点 求a的值.
16.在同一平面直角坐标系内画出一次函数 和 的图象,根据图象回答下列问题:
(1)求方程组 的解;
(2)当x取何值时, 当x取何值时, 且
四、(本大题共2 小题,每小题8分,满分16 分)
17.在第1个 中, 在 上取一点 C,延长 到点. 使得 在 上取一点 D,延长. 到点 使得 按此做法进行下去.求:
(1)第2个三角形的以 为顶点的内角的度数;
(2)第n个三角形的以 为顶点的内角的度数.
18.如图, ,求 各内角的度数.
五、(本大题共2 小题,每小题10 分,满分20 分)
19.某农产品店利用网络将优质土特产销往全国,其中销售的核桃和花生这两种商品的相关信息如下表.根据下表提供的信息,解答下列问题:
商品 核桃 花生
规格 1 kg/袋 2 kg/袋
利润 10元/袋 8元/袋
(1)已知今年上半年,该店销售上表规格的核桃和花生共3 000kg,获得利润21 000 元,求上半年该店销售这种规格的核桃和花生各多少袋
(2)根据之前的销售情况,估计今年下半年该店还能销售上表规格的核桃和花生共2 000kg,其中,核桃的销售量不低于600 kg.假设今年下半年,销售上表规格的核桃为x(kg),销售上表规格的核桃和花生获得的总利润为 W(元),写出W与x之间的函数表达式,并求下半年该店销售这种规格的核桃和花生至少获得的总利润.
20.如图,在 中,点E,F 分别在AB,AC 上,AD 是EF的垂直平分线, EF 交 AD 于点 G.
(1)求证:AD平分.
(2)若 求证:
六、(本题满分12 分)
21.工厂某车间需加工一批零件,甲组工人加工中因故停产检修机器一次,然后以原来的工作效率继续加工,由于时间紧任务重,乙组工人也加入共同加工零件.设甲组加工时间为t(时),甲组加工零件的数量为y甲(个),乙组加工零件的数量为yz(个),其函数图象如图所示.
(1)求yz 与t之间的函数表达式,并写出t的取值范围;
(2)求a的值,并说明a的实际意义;
(3)甲组加工多长时间时,甲、乙两组加工零件的总数为480 个.
七、(本题满分12 分)
22.如图,在平面直角坐标系中,直线 与x轴交于点A,与y轴交于点B,已知 ,点 P 是第一象限内在直线AB 上一点.
(1)直接写出k,b的值;
(2)设P(x,y),求 的面积S与x的函数表达式;
(3)当 时,求点 P 的坐标.
八、(本题满分14分)
23.如图1,在 中, 点D 是线段CA 延长线上一点,且. AB,点 F 是线段AB上一点,连接DF,以DF 为斜边作等腰 连接 EA,EA 满足条件
(1)若 ,求AB的长度;
(2)求证:
(3)如图2,点 F 是线段BA 延长线上一点,探究 AE,AF,BC 之间的数量关系,并证明你的结论.
期末综合检测卷
1. A 2. C 3. B 4. C 5. C 6. B 7. D 8. A 9. C 10. D
11.对应角相等的三角形是全等三角形 12.3 13.130°14.6
15.解:∵正比例函数y=kx的图象经过点.A(-1,3),B(a,a+1), 解得 ∴a的值为
16.解:画出一次函数 和 的图象如图.
(1)∵一次函数 和 的图象相交于点(3,1),∴ 方程组 的解为
(2)由图可知,当x<3时,y >y ;当x<2.5时,,y >0且
17.解:(1)∵在△ABA 中,
1是△A A C的外角,∴
(2)同(1)可得 ∴第n个三角形的以An为顶角的内角
18.解:∵∠FDE=∠BAD+∠ABD,∠BAD=∠CBE,∠FDE=64°,∴∠FDE=∠ABD+∠CBE=∠ABC.∴∠ABC=64°.
同理可得,∠DEF=∠FCB+∠CBE=∠FCB+∠ACF=∠ACB.又∵∠DEF=43°,∴∠ACB=43°.∴∠BAC=180°-∠ABC-∠ACB=180°-64°-43°=73°.
∴△ABC各内角的度数分别为64°,43°,73°.
19.解:(1)设今年上半年农产品店销售这种规格的核桃mkg,花生(3 000-m) kg.根据题意,得 解得m=1 500.
(袋).
答:今年上半年农产品店销售这种规格的核桃1 500袋和花生750 袋.
(2)根据题意,得
∵600≤x<2000,且6>0,∴W随x的增大而增大.
∴当x=600时,W有最小值, (元).
答:下半年该农产品店销售这种规格的核桃和花生至少获得的总利润为11 600 元.
20.证明:(1)∵AD 是EF的垂直平分线,∴DE=DF.
∵DE⊥AB,DF⊥AC,∴AD平分∠BAC.
(2)∵∠BAC=60°,AD平分
∵DE⊥AB,DF⊥AC,AD⊥EF,∴∠EAD+∠AEG=∠DEG+∠AEG=90°.
∴∠DEG=∠EAD=30°.∴DE=2DG.
21.解:(1)设yz与t之间的函数表达式是
根据题意,得yz 的图象过点(5,0)和(8,360),代入 得 解得
∴yz与t之间的函数表达式是:
(2)由图象可得,甲的工作效率为120÷3=40(个/时).
a=120+40×(8-4)=280,即a的值是280.
实际意义是当甲加工8小时时,一共加工了280个零件.
(3)设甲组加工c小时时,甲、乙两组加工零件的总数为480 个.根据题意,得120+40(c-4)+(120c-600)=480.解得c=7.即甲组加工7小时时,甲、乙两组加工零件的总数为480个.
22.解:(1)k= -1,b=6.
(2)如图,过点P作PH⊥OA于点H.
∵点P(x,y)是第一象限内在直线y=-x+6上一点,
∴PH= -x+6(0
又∵PH⊥OA,OA=6,OP=AP,
∴OH=HA=3,∠HPA=∠PAH=45°.∴AH=PH=3.∴点P的坐标为(3,3).
23.(1)解:如图1,∵在等腰直角三角形DEF 中,∠DEF=90°,∠1=20°,
∴∠2=∠DEF--∠1=70°.
∵∠ADE+∠2+∠3=180°,∠ADE=50°,∴∠3=60°.
∵EA⊥AB,∴∠EAB=90°.∵∠3+∠EAB+∠4=180°,∴∠4=30°.
∵∠C=90°,∴AB=2BC=4.
(2)证明:如图1,过点 D作DM⊥AE于点M,在△DEM中,∠2+∠5=90°.
∵∠2 +∠1=90°,∴∠1 =∠5.
在△DEM 和△EFA中,(200°,∴△DEM≌△EFA(AAS).∴AF=ME.
∵∠3+∠EAB+∠4=180°,∠EAB=90°,∴∠3+∠4=90°.
∵∠C=90°,∴∠4+∠B=90°.∴∠3=∠B.
在△DAM 和△ABC中
∴BC=AM.∴AE=ME+AM=AF+BC.
(3)解:AE+AF=BC.证明如下:
如图2,过点 D作DM⊥AE交AE的延长线于点 M.
∵∠C=90°,∴∠1 +∠B=90°.
∵∠2+∠MAB+∠1=180°,∠MAB=90°,∴∠2+∠1=90°.∴∠2=∠B.
在△ADM 和△BAC中,
∵∠3+∠DEF+∠4=180°,∠DEF=90°,∴∠3 +∠4=90°.
∵∠M=90°,∴∠3+∠5 =90°.∴∠4=∠5.
在△MED 和△AFE中,
∴AE+AF=AE+ME=AM=BC,即AE+AF=BC.
同课章节目录
