九年级数学上册 21.6 综合与实践 获取最大利润 导学案(知识清单 典型例题 巩固提升)
文档属性
| 名称 | 九年级数学上册 21.6 综合与实践 获取最大利润 导学案(知识清单 典型例题 巩固提升) |

|
|
| 格式 | docx | ||
| 文件大小 | 671.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-07 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
21.6 综合与实践 获取最大利润 导学案
(一)学习目标:
1.能应用二次函数的性质解决商品销售过程中的最大利润问题.
2.弄清商品销售问题中的数量关系及确定自变量的取值范围.
(二)学习重难点:
重点:用二次函数的性质解决商品销售过程中的最大利润问题
难点:商品销售问题中的数量关系及确定自变量的取值范围
阅读课本,识记知识:
(1)利用二次函数解决利润问题
在商品经营活动中,经常会遇到求最大利润,最大销量等问题.解此类题的关键是通过题意,确定出二次函数的解析式,然后确定其最大值,实际问题中自变量x的取值要使实际问题有意义,因此在求二次函数的最值时,一定要注意自变量x的取值范围.
(2)几何图形中的最值问题
几何图形中的二次函数问题常见的有:几何图形中面积的最值,用料的最佳方案以及动态几何中的最值的讨论.
(3)构建二次函数模型解决实际问题
利用二次函数解决抛物线形的隧道、大桥和拱门等实际问题时,要恰当地把这些实际问题中的数据落实到平面直角坐标系中的抛物线上,从而确定抛物线的解析式,通过解析式可解决一些测量问题或其他问题.
【例1】某药店对一种消毒液5天中的售价与销量进行调查,销量是售价的函数(统计数据见下表).已知该消毒液的进价为22元/瓶,则下列说法正确的是( )
售价x(元/瓶) 24 25 30 32 37.5
销售y(瓶) 200 192 160 150 128
A.销量是售价的正比例函数
B.每天的利润是售价的正比例函数
C.每天的利润是售价的反比例函数
D.要使每天的利润达到1600元,售价应为33元/瓶
【答案】D
【分析】根据反比例函数的意义计算售价和销售量的乘积,即可判断A,再求出利润的表达式,即可判断B,C,根据利润为1600元列出方程,解之即可判断D.
【详解】解:由表可知:
,
∴销量是售价的反比例函数,故A不合题意;
每天的利润为:
故每天的利润既不是售价的正比例函数,也不是反比例函数,故B,C不合题意;
要使每天的利润达到1600元,
则,
解得:,即售价为33元/瓶,故D符合题意;
故选D.
【点睛】本题考查了正比例函数和反比例函数,解答本题的关键是正确利用表格中的数据,掌握销售问题中的等量关系.
【例2】在经济学上,通常可以用反比例函数来描述商品需求量与价格之间的关系.假设市场上某商品的需求量D与价格P之间的关系可以用D=k/p(k常数)来表示,当该商品价格为50元时,需求量为100件.若该商品价格控制在100≤P≤200的范围内, 那么需求量力的范围为( )
A.25≤D≤50 B.0≤D≤50 C. D≥25 D.50≤D≤100
[答案] A
[分析]本题考查了反比例函数的应用,根据题意,先求出反比例函数解析式,根据条件列出关于D的不等式组,解出不等式组的解集即可.
[详解]解:当该商品价格为50元时,需求量为100件.
k= 50x 100 = 5000.
反比例函数解析式为D= 5000 ,
当商品价格控制在100≤P≤200的范围内时则有1005000≤200,
解得: 25≤D≤50,
故选: A.
选择题
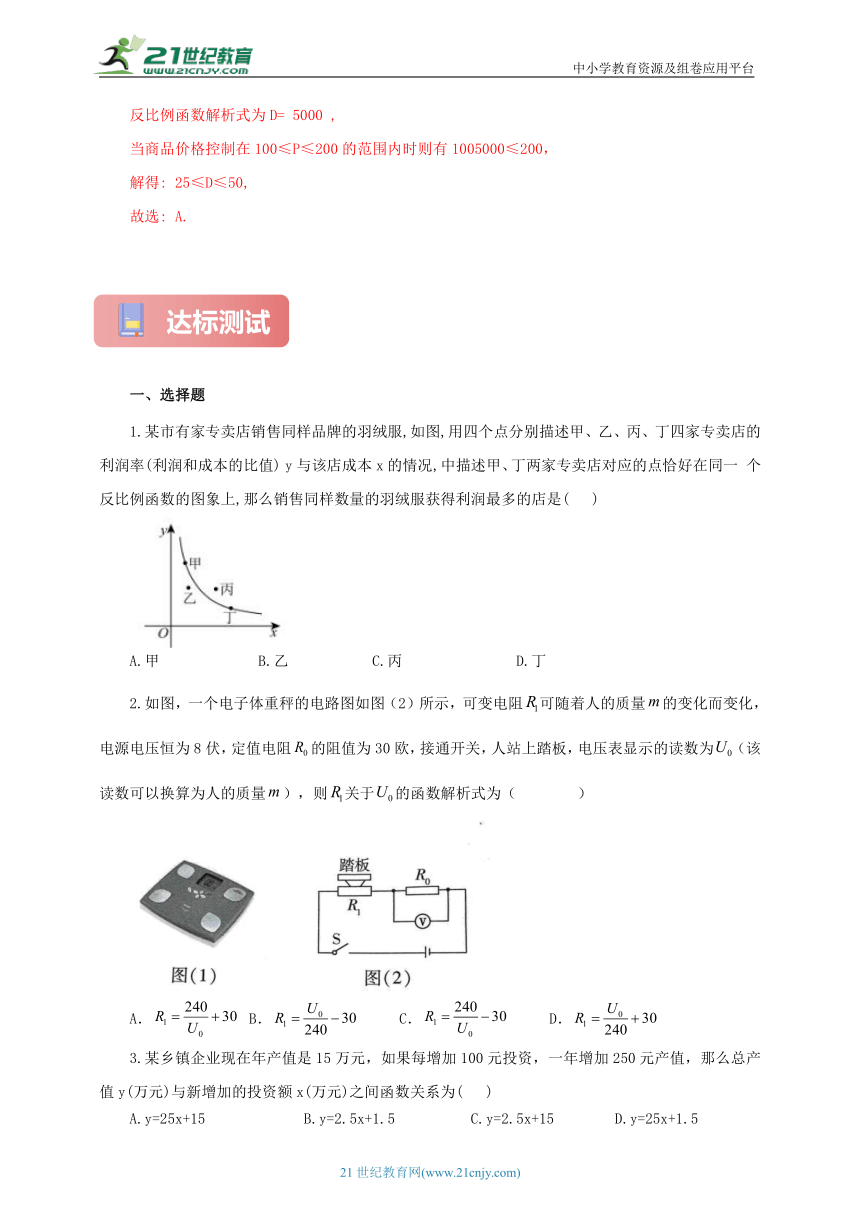
1.某市有家专卖店销售同样品牌的羽绒服,如图,用四个点分别描述甲、乙、丙、丁四家专卖店的利润率(利润和成本的比值) y与该店成本x的情况,中描述甲、丁两家专卖店对应的点恰好在同一 个反比例函数的图象上,那么销售同样数量的羽绒服获得利润最多的店是( )
A.甲 B.乙 C.丙 D.丁
2.如图,一个电子体重秤的电路图如图(2)所示,可变电阻可随着人的质量的变化而变化,电源电压恒为8伏,定值电阻的阻值为30欧,接通开关,人站上踏板,电压表显示的读数为(该读数可以换算为人的质量),则关于的函数解析式为( )
A. B. C. D.
3.某乡镇企业现在年产值是15万元,如果每增加100元投资,一年增加250元产值,那么总产值y(万元)与新增加的投资额x(万元)之间函数关系为( )
A.y=25x+15 B.y=2.5x+1.5 C.y=2.5x+15 D.y=25x+1.5
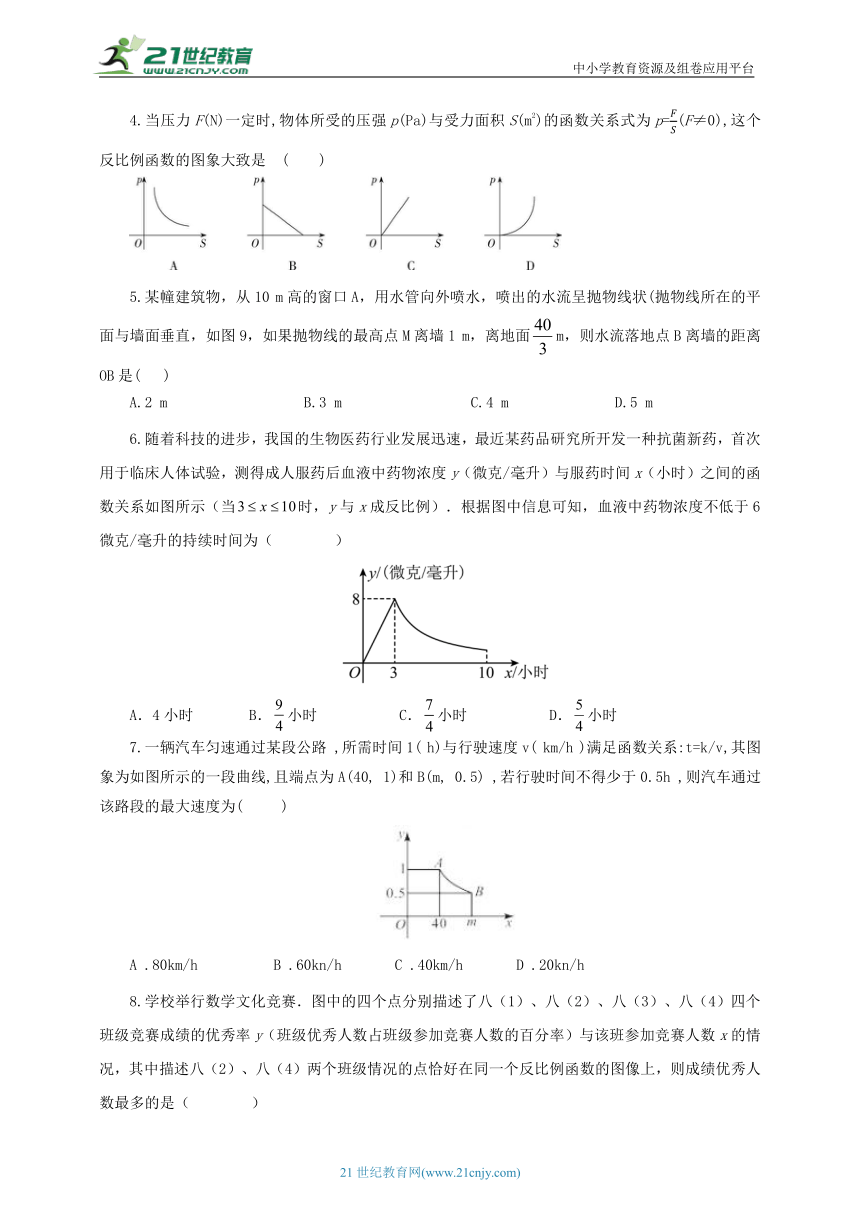
4.当压力F(N)一定时,物体所受的压强p(Pa)与受力面积S(m2)的函数关系式为p=(F≠0),这个反比例函数的图象大致是 ( )
5.某幢建筑物,从10 m高的窗口A,用水管向外喷水,喷出的水流呈抛物线状(抛物线所在的平面与墙面垂直,如图9,如果抛物线的最高点M离墙1 m,离地面m,则水流落地点B离墙的距离OB是( )
A.2 m B.3 m C.4 m D.5 m
6.随着科技的进步,我国的生物医药行业发展迅速,最近某药品研究所开发一种抗菌新药,首次用于临床人体试验,测得成人服药后血液中药物浓度y(微克/毫升)与服药时间x(小时)之间的函数关系如图所示(当时,y与x成反比例).根据图中信息可知,血液中药物浓度不低于6微克/毫升的持续时间为( )
A.4小时 B.小时 C.小时 D.小时
7.一辆汽车匀速通过某段公路 ,所需时间1( h)与行驶速度v( km/h )满足函数关系:t=k/v,其图象为如图所示的一段曲线,且端点为A(40, 1)和B(m, 0.5) ,若行驶时间不得少于0.5h ,则汽车通过该路段的最大速度为( )
A .80km/h B .60kn/h C .40km/h D .20kn/h
8.学校举行数学文化竞赛.图中的四个点分别描述了八(1)、八(2)、八(3)、八(4)四个班级竞赛成绩的优秀率y(班级优秀人数占班级参加竞赛人数的百分率)与该班参加竞赛人数x的情况,其中描述八(2)、八(4)两个班级情况的点恰好在同一个反比例函数的图像上,则成绩优秀人数最多的是( )
A.八(1)班 B.八(2)班 C.八(3)班 D.八(4)班
9.某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压()是气体体积()的反比例函数,如图,当气球内的气压大于时,气球将爆炸,为了安全起见,气球体积应( ).
A. B. C. D.
填空题
10.根据某商场对一款运动鞋五天中的售价与销量关系的调查显示,售价是销量的反比例函数(统计数据见下表).已知该运动鞋的进价为180元/双,要使该款运动鞋每天的销售利润达到2 400元,则其售价应定为 元/双.
售价x(元/双) 200 240 250 400
销售量y(双) 30 25 24 15
11.一辆汽车前灯电路上的电压U(V)保持不变,通过灯泡的电流强度I(A)是电阻R(Ω)的反比例函数.若当电阻为30 Ω时,通过灯泡的电流强度为0.40 A,则当电阻为50 Ω时,通过灯泡的电流强度为 A.
12.已知A(-14,y1),B(-15,y2)两点在双曲线y=上,当y1>y2时,m的取值范围是 .
13.如图,一次函数y=6x与反比例函数y=(k>0)的图象交于A、B两点,点C在x轴上运动,连接AC,点Q为AC中点,在点C运动过程中,OQ的最小值为2,则k= .
14.将进货单价为70元的某种商品按零售价100元售出时,每天能卖出20个.若这种商品的
零售价在一定范围内每降价1元,其日销售量就增加了1个,为了获得最大利润,则应降价______元,最大利润为______元.
三、解答题
15.码头工人每天往一艘轮船上装载货物,平均每天装载速度y(吨/天)与装完货物所需时间x(天)之间是反比例函数关系,其图像如图:
(1)求这个反比例函数的解析式;
(2)装载完毕后,由于遇到紧急情况,要求船上的货物不超过5天卸货完毕,那么平均每天至少卸货多少吨?
16.某工厂生产A产品x吨所需费用为P元,而卖出x吨这种产品的售价为每吨Q元, 已知P=x2+5x+1000,Q=-+45.
(1)该厂生产并售出x吨,写出这种产品所获利润W(元)关于x(吨)的函数关系式;
(2)当生产多少吨这种产品,并全部售出时,获利最多 这时获利多少元 这时每吨的价格又是多少元
17.某商场以每件20元的价格购进一种商品,试销中发现,这种商品每天的销售量m(件)与每件的销售价x(元)满足关系:m=140-2x.
(1)写出商场卖这种商品每天的销售利润y与每件的销售价x间的函数关系式;
(2)如果商场要想每天获得最大的销售利润,每件商品的售价定为多少最合适?最大销售利润为多少?
18.某水果店去年2月至5月份销售甲乙两种新鲜水果,已知甲种水果每月售价与月份x之间存在的反比例函数关系如表所示.
时间x/月份 2 3 4 5
售价 /(元/千克) 12 8 6
甲种水果进价为3元/千克,销售量P(千克)与x之间满足关系式;乙种水果每月售价与月份x之间满足,对应的图象如图所示.乙种水果进价为元/千克,平均每月销售160千克.
(1)求与x之间的函数关系式;
(2)求与x之间的函数关系式;
(3)若水果店销售水果时需要缴纳元/千克的税费,问该水果店哪个月销售甲乙两种水果获得的总利润最大,最大利润是多少?
(一)课后反思:
本节课我学会了:
本节课存在的问题:
把本节课所学知识画出思维导图
参考答案
1.[答案] C
[分析]本题考查反比例函数的实际应用,根据图象获取信息。即可得出结果.
[详解]解:。甲、丁两家专卖店对应的点恰好在同-一个反比例函数的图象上,
当销售同样数量的羽绒服时,甲,丁的利润相等,
丙在双曲线的.上方,乙在双曲线的下方,
小当销售同样数量的羽绒服时,丙的利润大于甲,丁的利润,乙的利润小于甲,丁的利润.
故选C.
2.C
【分析】通过串联电路中电流处处相等和可以列出等量关系,然后再化简为关于的函数解析式
【详解】由题意得:可变电阻两端的电压=电源电压-电表电压,
即:可变电阻电压,
∵,可变电阻和定值电阻的电流大小相等,
∴.
化简得:,
∵,
∴.
故选:C
【点睛】本题以物理中的电路问题为背景,考查了学生对于反比例函数关系式的掌握情况,解题的关键是先要求找出两个要求量之间的等量关系,然后化简为要求的表达式,转化过程中需要注意无关量的消去,一般情况下都是用代入法消元来解决这一问题的.
3.C
【答案】 A
【分析】当F(F>0)一定时,p与S之间成反比,则函数图象是双曲线位于第一象限的分支.故选A.
5.B〔提示:设水流的解析式为y=a(x-h)2+k,
∴A(0,10),M(1,).
∴y=a(x-1)2+,10=a+.
∴a=-.
∴y=-(x-1)2+.
令y=0得x=-1或x=3得B(3,0),
即B点离墙的距离OB是3 m
6.A
【分析】设密度是体积的反比例函数为,把点代入解析式,根据待定系数法求得的值和函数解析式,再将代入函数,即可解答.
【详解】解:设密度是体积的反比例函数为,
把点代入解析式,可得,解得,
,
当时,(),
故选:A.
【点睛】本题考查了反比例函数的应用,解答该类问题的关键是确定两个变量之间的关系,再利用待定系数法求出他们的解析式.
7.[答案] A
[分析]本题考查了反比例函数的应用,现实生活中存在大量成反比例函数的两个变量,解答该类问题的关键是确定两个变量之间的函数关系,然后利用待定系数法求出它们的关系式.
将点4(40, 1)代入-告可得k,把B(m, 0.5)代入求出m= 80,即可得到答案.
[详解]解:由题意得,函数经过点4(40, 1) .
把4(40. 1)代入,得k=40
函数解析式为t=40/v ,
行驶时间不得少于0.5h,
把B(m, 0.5)代入,得0.5=-40/m
M=80
汽车通过该路段的最大速度为80km/h.
故选: A.
8.A
【分析】设反比例函数表达式为,过八(1)点,八(3)点作轴的平行线交反比例函数于,,设八(1)点为,,八(2)点为,,八(3)点为,,八(4)点为,,点为,,点为,,然后比较,,,与的大小即可得出答案.
【详解】解:设反比例函数的表达式为,
过八(1)点,八(3)点作轴的平行线交反比例函数于,,
设八(1)点为,,八(2)点,,八(3)点为,,八(4)点,,点为,,点为,,
由图象可知:,,
依题意得:,,,分别为八(1),八(2),八(3),八(4)的优秀人数.
八(2)点,点,点,八(4)点在反比例函数的图象上,
,
,,
,,
,
即:八(1)班优秀人数八(2)班优秀人数八(4)班优秀人数八(3)班优秀人数,
八(1)班的优秀人数为最多.
故选:A.
【点睛】本题主要考查反比例函数图象与性质的实际应用,读懂题意,熟练掌握反比例函数的图象与性质是解决问题的关键.
9.A
【分析】由题意得与成反比例,设气球内气体的气压和气体的体积之间的函数关系式为,代入,求出解析式,由,求出的范围即可.
【详解】解:设气球内气体的气压和气体的体积之间的函数关系式为,
∵图象过,
∴,
解得,,
∴,
∵在第一象限内随的增大而减小,
∴当时,,即,
故选:A.
【点睛】本题考查了求反比例函数的解析式,反比例函数的应用,解题的关键是根据图象上已知点的坐标,利用待定系数法求出函数解析式.
10.【答案】 300
【解析】 由表中数据得xy=6 000,
∴y=,
则函数解析式为y=.
由题意,得(x-180)y=2 400,
把y=代入得(x-180)·=2 400,
解得x=300,
经检验,x=300是原方程的解,
∴单价应定为300元.
11. 【答案】 0.24
【解析】由题意可得I=,∵当电阻为30 Ω时,通过灯泡的电流强度为0.40 A,∴U=30×0.40=12(V),∴I=,当电阻为50 Ω时,I==0.24(A).
12.【答案】 m<-16
【解析】 ∵A(-14,y1),B(-15,y2)两点在双曲线y=上,
且-15<-14<0,y1>y2,
∴在每个象限内,y随x的增大而增大,
∴m+16<0,解得m<-16.
13.【答案】
【解析】 连接CB,由题意可知点A、B关于原点对称,故O是AB的中点,又Q为AC中点,故OQ是△ABC的中位线,则OQ=BC,故当BC最短时,OQ也最短,当BC⊥x轴时,BC最短,此时BC=2OQ=4,即点B的纵坐标为-4,将点B的纵坐标代入y=6x得-4=6x,解得x=-,故点B的坐标为,∵点B在反比例函数y=(k>0)的图象上,∴k=-×(-4)=.
14.5 625
15.(1)
(2)平均每天至少要卸80吨货物
【分析】(1)根据待定系数法求出反比例函数解析式即可;
(2)把代入函数解析式求出函数解析式即可.
【详解】(1)解:设与的函数解析式为,
依题意得:,,
∴y与x的函数解析式为;
(2)解:把代入得:,
答:平均每天至少要卸80吨货物.
【点睛】本题主要考查了反比例函数的应用,解题的关键是求出反比例函数解析式.
16.(1)∵P=x2+5x+1000,Q=-+45.
∴W=Qx-P=(-+45)-(x2+5x+1000)= .
(2)∵W==-(x-150)2+2000.
∵-<0,∴W有最大值.
当x=150吨时,利润最多,最大利润2000元.
当x=150吨,Q=-+45=40(元).
17.(1)y=-2x2+180x-2800.
(2)y=-2x2+180x-2800
=-2(x2-90x)-2800
=-2(x-45)2+1250.
当x=45时,y最大=1250.
∴每件商品售价定为45元最合适,此销售利润最大,为1250元.
18.(1)为整数)
(2),且x为整数)
(3)水果店2月份销售甲乙两种水果获得的总利润最大,最大利润是720元
【分析】(1)根据表中数据,用待定系数法求函数解析式即可;
(2)根据图象用待定系数法求函数解析式即可;
(3)根据总利润等于甲乙两种水果利润之和列出函数解析式,根据函数的性质求最值即可.
【详解】(1)解:设与x之间的函数关系式为 ,
把代入解析式,则 ,
解得,
∴与x之间的函数关系式为为整数);
(2)解:把代入,得:
,解得 ,
∴与x之间的函数关系式为,且x为整数);
(3)解:设甲乙两种水果获得的总利润为w,则
,
=
,
对称轴为直线 .
∵,
∴当时,w随x的增大而减小.
∵x为整数,
∴当时,w有最大值,最大值(元),
答:水果店2月份销售甲乙两种水果获得的总利润最大,最大利润是720元.
【点睛】本题考查反比例函数和二次函数的应用,关键是用待定系数法求函数解析式.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
21.6 综合与实践 获取最大利润 导学案
(一)学习目标:
1.能应用二次函数的性质解决商品销售过程中的最大利润问题.
2.弄清商品销售问题中的数量关系及确定自变量的取值范围.
(二)学习重难点:
重点:用二次函数的性质解决商品销售过程中的最大利润问题
难点:商品销售问题中的数量关系及确定自变量的取值范围
阅读课本,识记知识:
(1)利用二次函数解决利润问题
在商品经营活动中,经常会遇到求最大利润,最大销量等问题.解此类题的关键是通过题意,确定出二次函数的解析式,然后确定其最大值,实际问题中自变量x的取值要使实际问题有意义,因此在求二次函数的最值时,一定要注意自变量x的取值范围.
(2)几何图形中的最值问题
几何图形中的二次函数问题常见的有:几何图形中面积的最值,用料的最佳方案以及动态几何中的最值的讨论.
(3)构建二次函数模型解决实际问题
利用二次函数解决抛物线形的隧道、大桥和拱门等实际问题时,要恰当地把这些实际问题中的数据落实到平面直角坐标系中的抛物线上,从而确定抛物线的解析式,通过解析式可解决一些测量问题或其他问题.
【例1】某药店对一种消毒液5天中的售价与销量进行调查,销量是售价的函数(统计数据见下表).已知该消毒液的进价为22元/瓶,则下列说法正确的是( )
售价x(元/瓶) 24 25 30 32 37.5
销售y(瓶) 200 192 160 150 128
A.销量是售价的正比例函数
B.每天的利润是售价的正比例函数
C.每天的利润是售价的反比例函数
D.要使每天的利润达到1600元,售价应为33元/瓶
【答案】D
【分析】根据反比例函数的意义计算售价和销售量的乘积,即可判断A,再求出利润的表达式,即可判断B,C,根据利润为1600元列出方程,解之即可判断D.
【详解】解:由表可知:
,
∴销量是售价的反比例函数,故A不合题意;
每天的利润为:
故每天的利润既不是售价的正比例函数,也不是反比例函数,故B,C不合题意;
要使每天的利润达到1600元,
则,
解得:,即售价为33元/瓶,故D符合题意;
故选D.
【点睛】本题考查了正比例函数和反比例函数,解答本题的关键是正确利用表格中的数据,掌握销售问题中的等量关系.
【例2】在经济学上,通常可以用反比例函数来描述商品需求量与价格之间的关系.假设市场上某商品的需求量D与价格P之间的关系可以用D=k/p(k常数)来表示,当该商品价格为50元时,需求量为100件.若该商品价格控制在100≤P≤200的范围内, 那么需求量力的范围为( )
A.25≤D≤50 B.0≤D≤50 C. D≥25 D.50≤D≤100
[答案] A
[分析]本题考查了反比例函数的应用,根据题意,先求出反比例函数解析式,根据条件列出关于D的不等式组,解出不等式组的解集即可.
[详解]解:当该商品价格为50元时,需求量为100件.
k= 50x 100 = 5000.
反比例函数解析式为D= 5000 ,
当商品价格控制在100≤P≤200的范围内时则有1005000≤200,
解得: 25≤D≤50,
故选: A.
选择题
1.某市有家专卖店销售同样品牌的羽绒服,如图,用四个点分别描述甲、乙、丙、丁四家专卖店的利润率(利润和成本的比值) y与该店成本x的情况,中描述甲、丁两家专卖店对应的点恰好在同一 个反比例函数的图象上,那么销售同样数量的羽绒服获得利润最多的店是( )
A.甲 B.乙 C.丙 D.丁
2.如图,一个电子体重秤的电路图如图(2)所示,可变电阻可随着人的质量的变化而变化,电源电压恒为8伏,定值电阻的阻值为30欧,接通开关,人站上踏板,电压表显示的读数为(该读数可以换算为人的质量),则关于的函数解析式为( )
A. B. C. D.
3.某乡镇企业现在年产值是15万元,如果每增加100元投资,一年增加250元产值,那么总产值y(万元)与新增加的投资额x(万元)之间函数关系为( )
A.y=25x+15 B.y=2.5x+1.5 C.y=2.5x+15 D.y=25x+1.5
4.当压力F(N)一定时,物体所受的压强p(Pa)与受力面积S(m2)的函数关系式为p=(F≠0),这个反比例函数的图象大致是 ( )
5.某幢建筑物,从10 m高的窗口A,用水管向外喷水,喷出的水流呈抛物线状(抛物线所在的平面与墙面垂直,如图9,如果抛物线的最高点M离墙1 m,离地面m,则水流落地点B离墙的距离OB是( )
A.2 m B.3 m C.4 m D.5 m
6.随着科技的进步,我国的生物医药行业发展迅速,最近某药品研究所开发一种抗菌新药,首次用于临床人体试验,测得成人服药后血液中药物浓度y(微克/毫升)与服药时间x(小时)之间的函数关系如图所示(当时,y与x成反比例).根据图中信息可知,血液中药物浓度不低于6微克/毫升的持续时间为( )
A.4小时 B.小时 C.小时 D.小时
7.一辆汽车匀速通过某段公路 ,所需时间1( h)与行驶速度v( km/h )满足函数关系:t=k/v,其图象为如图所示的一段曲线,且端点为A(40, 1)和B(m, 0.5) ,若行驶时间不得少于0.5h ,则汽车通过该路段的最大速度为( )
A .80km/h B .60kn/h C .40km/h D .20kn/h
8.学校举行数学文化竞赛.图中的四个点分别描述了八(1)、八(2)、八(3)、八(4)四个班级竞赛成绩的优秀率y(班级优秀人数占班级参加竞赛人数的百分率)与该班参加竞赛人数x的情况,其中描述八(2)、八(4)两个班级情况的点恰好在同一个反比例函数的图像上,则成绩优秀人数最多的是( )
A.八(1)班 B.八(2)班 C.八(3)班 D.八(4)班
9.某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压()是气体体积()的反比例函数,如图,当气球内的气压大于时,气球将爆炸,为了安全起见,气球体积应( ).
A. B. C. D.
填空题
10.根据某商场对一款运动鞋五天中的售价与销量关系的调查显示,售价是销量的反比例函数(统计数据见下表).已知该运动鞋的进价为180元/双,要使该款运动鞋每天的销售利润达到2 400元,则其售价应定为 元/双.
售价x(元/双) 200 240 250 400
销售量y(双) 30 25 24 15
11.一辆汽车前灯电路上的电压U(V)保持不变,通过灯泡的电流强度I(A)是电阻R(Ω)的反比例函数.若当电阻为30 Ω时,通过灯泡的电流强度为0.40 A,则当电阻为50 Ω时,通过灯泡的电流强度为 A.
12.已知A(-14,y1),B(-15,y2)两点在双曲线y=上,当y1>y2时,m的取值范围是 .
13.如图,一次函数y=6x与反比例函数y=(k>0)的图象交于A、B两点,点C在x轴上运动,连接AC,点Q为AC中点,在点C运动过程中,OQ的最小值为2,则k= .
14.将进货单价为70元的某种商品按零售价100元售出时,每天能卖出20个.若这种商品的
零售价在一定范围内每降价1元,其日销售量就增加了1个,为了获得最大利润,则应降价______元,最大利润为______元.
三、解答题
15.码头工人每天往一艘轮船上装载货物,平均每天装载速度y(吨/天)与装完货物所需时间x(天)之间是反比例函数关系,其图像如图:
(1)求这个反比例函数的解析式;
(2)装载完毕后,由于遇到紧急情况,要求船上的货物不超过5天卸货完毕,那么平均每天至少卸货多少吨?
16.某工厂生产A产品x吨所需费用为P元,而卖出x吨这种产品的售价为每吨Q元, 已知P=x2+5x+1000,Q=-+45.
(1)该厂生产并售出x吨,写出这种产品所获利润W(元)关于x(吨)的函数关系式;
(2)当生产多少吨这种产品,并全部售出时,获利最多 这时获利多少元 这时每吨的价格又是多少元
17.某商场以每件20元的价格购进一种商品,试销中发现,这种商品每天的销售量m(件)与每件的销售价x(元)满足关系:m=140-2x.
(1)写出商场卖这种商品每天的销售利润y与每件的销售价x间的函数关系式;
(2)如果商场要想每天获得最大的销售利润,每件商品的售价定为多少最合适?最大销售利润为多少?
18.某水果店去年2月至5月份销售甲乙两种新鲜水果,已知甲种水果每月售价与月份x之间存在的反比例函数关系如表所示.
时间x/月份 2 3 4 5
售价 /(元/千克) 12 8 6
甲种水果进价为3元/千克,销售量P(千克)与x之间满足关系式;乙种水果每月售价与月份x之间满足,对应的图象如图所示.乙种水果进价为元/千克,平均每月销售160千克.
(1)求与x之间的函数关系式;
(2)求与x之间的函数关系式;
(3)若水果店销售水果时需要缴纳元/千克的税费,问该水果店哪个月销售甲乙两种水果获得的总利润最大,最大利润是多少?
(一)课后反思:
本节课我学会了:
本节课存在的问题:
把本节课所学知识画出思维导图
参考答案
1.[答案] C
[分析]本题考查反比例函数的实际应用,根据图象获取信息。即可得出结果.
[详解]解:。甲、丁两家专卖店对应的点恰好在同-一个反比例函数的图象上,
当销售同样数量的羽绒服时,甲,丁的利润相等,
丙在双曲线的.上方,乙在双曲线的下方,
小当销售同样数量的羽绒服时,丙的利润大于甲,丁的利润,乙的利润小于甲,丁的利润.
故选C.
2.C
【分析】通过串联电路中电流处处相等和可以列出等量关系,然后再化简为关于的函数解析式
【详解】由题意得:可变电阻两端的电压=电源电压-电表电压,
即:可变电阻电压,
∵,可变电阻和定值电阻的电流大小相等,
∴.
化简得:,
∵,
∴.
故选:C
【点睛】本题以物理中的电路问题为背景,考查了学生对于反比例函数关系式的掌握情况,解题的关键是先要求找出两个要求量之间的等量关系,然后化简为要求的表达式,转化过程中需要注意无关量的消去,一般情况下都是用代入法消元来解决这一问题的.
3.C
【答案】 A
【分析】当F(F>0)一定时,p与S之间成反比,则函数图象是双曲线位于第一象限的分支.故选A.
5.B〔提示:设水流的解析式为y=a(x-h)2+k,
∴A(0,10),M(1,).
∴y=a(x-1)2+,10=a+.
∴a=-.
∴y=-(x-1)2+.
令y=0得x=-1或x=3得B(3,0),
即B点离墙的距离OB是3 m
6.A
【分析】设密度是体积的反比例函数为,把点代入解析式,根据待定系数法求得的值和函数解析式,再将代入函数,即可解答.
【详解】解:设密度是体积的反比例函数为,
把点代入解析式,可得,解得,
,
当时,(),
故选:A.
【点睛】本题考查了反比例函数的应用,解答该类问题的关键是确定两个变量之间的关系,再利用待定系数法求出他们的解析式.
7.[答案] A
[分析]本题考查了反比例函数的应用,现实生活中存在大量成反比例函数的两个变量,解答该类问题的关键是确定两个变量之间的函数关系,然后利用待定系数法求出它们的关系式.
将点4(40, 1)代入-告可得k,把B(m, 0.5)代入求出m= 80,即可得到答案.
[详解]解:由题意得,函数经过点4(40, 1) .
把4(40. 1)代入,得k=40
函数解析式为t=40/v ,
行驶时间不得少于0.5h,
把B(m, 0.5)代入,得0.5=-40/m
M=80
汽车通过该路段的最大速度为80km/h.
故选: A.
8.A
【分析】设反比例函数表达式为,过八(1)点,八(3)点作轴的平行线交反比例函数于,,设八(1)点为,,八(2)点为,,八(3)点为,,八(4)点为,,点为,,点为,,然后比较,,,与的大小即可得出答案.
【详解】解:设反比例函数的表达式为,
过八(1)点,八(3)点作轴的平行线交反比例函数于,,
设八(1)点为,,八(2)点,,八(3)点为,,八(4)点,,点为,,点为,,
由图象可知:,,
依题意得:,,,分别为八(1),八(2),八(3),八(4)的优秀人数.
八(2)点,点,点,八(4)点在反比例函数的图象上,
,
,,
,,
,
即:八(1)班优秀人数八(2)班优秀人数八(4)班优秀人数八(3)班优秀人数,
八(1)班的优秀人数为最多.
故选:A.
【点睛】本题主要考查反比例函数图象与性质的实际应用,读懂题意,熟练掌握反比例函数的图象与性质是解决问题的关键.
9.A
【分析】由题意得与成反比例,设气球内气体的气压和气体的体积之间的函数关系式为,代入,求出解析式,由,求出的范围即可.
【详解】解:设气球内气体的气压和气体的体积之间的函数关系式为,
∵图象过,
∴,
解得,,
∴,
∵在第一象限内随的增大而减小,
∴当时,,即,
故选:A.
【点睛】本题考查了求反比例函数的解析式,反比例函数的应用,解题的关键是根据图象上已知点的坐标,利用待定系数法求出函数解析式.
10.【答案】 300
【解析】 由表中数据得xy=6 000,
∴y=,
则函数解析式为y=.
由题意,得(x-180)y=2 400,
把y=代入得(x-180)·=2 400,
解得x=300,
经检验,x=300是原方程的解,
∴单价应定为300元.
11. 【答案】 0.24
【解析】由题意可得I=,∵当电阻为30 Ω时,通过灯泡的电流强度为0.40 A,∴U=30×0.40=12(V),∴I=,当电阻为50 Ω时,I==0.24(A).
12.【答案】 m<-16
【解析】 ∵A(-14,y1),B(-15,y2)两点在双曲线y=上,
且-15<-14<0,y1>y2,
∴在每个象限内,y随x的增大而增大,
∴m+16<0,解得m<-16.
13.【答案】
【解析】 连接CB,由题意可知点A、B关于原点对称,故O是AB的中点,又Q为AC中点,故OQ是△ABC的中位线,则OQ=BC,故当BC最短时,OQ也最短,当BC⊥x轴时,BC最短,此时BC=2OQ=4,即点B的纵坐标为-4,将点B的纵坐标代入y=6x得-4=6x,解得x=-,故点B的坐标为,∵点B在反比例函数y=(k>0)的图象上,∴k=-×(-4)=.
14.5 625
15.(1)
(2)平均每天至少要卸80吨货物
【分析】(1)根据待定系数法求出反比例函数解析式即可;
(2)把代入函数解析式求出函数解析式即可.
【详解】(1)解:设与的函数解析式为,
依题意得:,,
∴y与x的函数解析式为;
(2)解:把代入得:,
答:平均每天至少要卸80吨货物.
【点睛】本题主要考查了反比例函数的应用,解题的关键是求出反比例函数解析式.
16.(1)∵P=x2+5x+1000,Q=-+45.
∴W=Qx-P=(-+45)-(x2+5x+1000)= .
(2)∵W==-(x-150)2+2000.
∵-<0,∴W有最大值.
当x=150吨时,利润最多,最大利润2000元.
当x=150吨,Q=-+45=40(元).
17.(1)y=-2x2+180x-2800.
(2)y=-2x2+180x-2800
=-2(x2-90x)-2800
=-2(x-45)2+1250.
当x=45时,y最大=1250.
∴每件商品售价定为45元最合适,此销售利润最大,为1250元.
18.(1)为整数)
(2),且x为整数)
(3)水果店2月份销售甲乙两种水果获得的总利润最大,最大利润是720元
【分析】(1)根据表中数据,用待定系数法求函数解析式即可;
(2)根据图象用待定系数法求函数解析式即可;
(3)根据总利润等于甲乙两种水果利润之和列出函数解析式,根据函数的性质求最值即可.
【详解】(1)解:设与x之间的函数关系式为 ,
把代入解析式,则 ,
解得,
∴与x之间的函数关系式为为整数);
(2)解:把代入,得:
,解得 ,
∴与x之间的函数关系式为,且x为整数);
(3)解:设甲乙两种水果获得的总利润为w,则
,
=
,
对称轴为直线 .
∵,
∴当时,w随x的增大而减小.
∵x为整数,
∴当时,w有最大值,最大值(元),
答:水果店2月份销售甲乙两种水果获得的总利润最大,最大利润是720元.
【点睛】本题考查反比例函数和二次函数的应用,关键是用待定系数法求函数解析式.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
