4.3 相似多边形 课件 (共19张PPT) 2024-2025学年数学北师版九年级上册
文档属性
| 名称 | 4.3 相似多边形 课件 (共19张PPT) 2024-2025学年数学北师版九年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 8.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-07 19:10:06 | ||
图片预览





文档简介
(共19张PPT)
4.3 相似多边形
1.认识相似图形和相似多边形.
2.会根据条件判断两个多边形是否为相似多边形.
3.掌握相似多边形的性质,能根据性质进行相关的计算.
放大镜下的图形和原来的图形有什么相同与不同吗?
相等.
放大镜下的角与原图形中角是什么关系?
边数不同
角不相等
边成比例
角相等
边不成比例
边成比例
角相等
不相似
不相似
不相似
相似
形状相同的图形叫做相似图形.
小组合作,尝试归纳出相似多边形的概念.
各角分别_______、各边_________的两个多边形叫做相似多边形.
相等
成比例
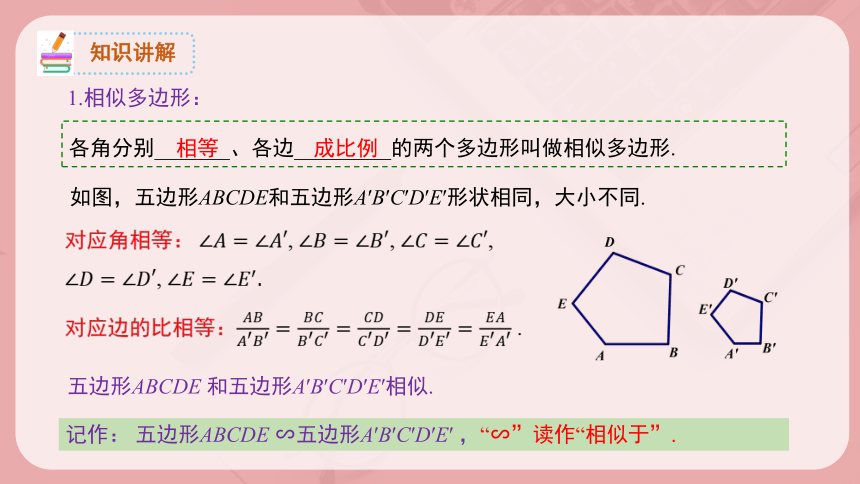
1.相似多边形:
如图,五边形ABCDE和五边形A′B′C′D′E′形状相同,大小不同.
对应边的比相等: .
对应角相等:, , ,
,
五边形ABCDE 和五边形A′B′C′D′E′相似.
记作: 五边形ABCDE ∽五边形A′B′C′D′E′ ,“∽”读作“相似于”.
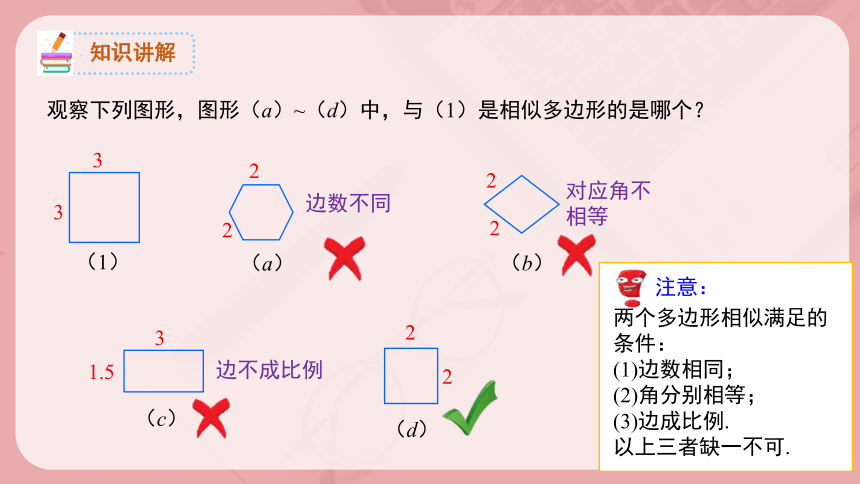
观察下列图形,图形(a)~(d)中,与(1)是相似多边形的是哪个?
1.5
3
(c)
边数不同
3
3
(1)
2
2
(b)
(a)
2
2
2
2
(d)
边不成比例
对应角不相等
注意:
两个多边形相似满足的条件:
(1)边数相同;
(2)角分别相等;
(3)边成比例.
以上三者缺一不可.
2.相似比:
相似多边形______________叫做相似比.
对应边的比
3
3
2
2
D1
C1
B1
A1
D
B
C
A
如图,正方形ABCD与正方形A1B1C1D1的相似比为 .
(1)相似比的值与两个多边形的前后顺序有关.
(2)相似比为1的两个相似多边形为全等多边形.
思考:正方形A1B1C1D1与正方形ABCD的相似比是多少?
3.相似多边形的性质:
相似多边形的_______________,__________________.
对应角相等
对应边的比相等
作用:常用来求相似多边形中未知的边的长度和角的度数.
利用相似多边形的性质求边长或角度,关键扣住“对应”二字,找准对应边和对应角是解决问题的关键.
需要注意的是对应边是比相等,而对应角是直接相等.
【例1】 下列四组图形中,一定相似的是( )
A.正方形和矩形 B.正方形和菱形
C.菱形和菱形 D.正方形与正方形
D
A.不一定相似
B.不一定相似
C.不一定相似
D.一定相似
′
′
′
′
【例2】已知:如图,梯形ABCD与梯形A′B′C′D′相似,AD∥BC,
A′D′∥B′C′,∠A=∠A′,AD=4,A′D′=6,AB=6,B′C′=12,∠C=60°.
(1)求梯形ABCD与梯形A′B′C′D′的相似比k的值;
(2)求A′B′和BC的长;
(3)求∠D′的大小.
解 :(1)相似比k=
(2)∵梯形ABCD与梯形A′B′C′D′相似,且由(1)知相似比k=
∴ ∵AB=6,B′C′=12,∴A′B′=9,BC=8.
【例2】已知:如图,梯形ABCD与梯形A′B′C′D′相似,AD∥BC,
A′D′∥B′C′,∠A=∠A′,AD=4,A′D′=6,AB=6,B′C′=12,∠C=60°.
(1)求梯形ABCD与梯形A′B′C′D′的相似比k的值;
(2)求A′B′和BC的长;
(3)求∠D′的大小.
(3)由题意知,∠D′=∠D.
∵AD∥BC,∠C=60°,
∴∠D=180°-∠C=120°. ∴∠D′=120°.
如果两个多边形不相似,那么它们的各角可能对应相等吗?
它们的各边可能对应成比例吗?
观察下面两组图形,图中的两个图形相似吗?为什么?
10
10
8
16
10
10
12
12
不相似
不相似
如果两个多边形不相似,那么它们的各角可能对应相等,它们的各边可能对应成比例.
【例3】如图所示,一块长为2米,宽为1米的矩形玻璃,为了保护玻璃需要镶上宽10厘米的铝合金边框,那么边框的内外边缘所成的矩形相似吗?为什么?
解:不相似. 由条件知, ,,所以.
所以两个矩形不相似.
应用一:判定两个多边形相似
应用二:应用多边形相似的性质解决问题
【例4】已知四边形ABCD与四边形A′B′C′D′相似,且AB∶BC∶CD∶DA=20∶15∶9∶8,四边形A′B′C′D′的周长为26,求四边形A′B′C′D′各边的长.
【分析】已知四边形ABCD与四边形A′B′C′D′相似,且AB∶BC∶CD∶DA=20∶15∶9∶8,则四边形A′B′C′D′的各边A′B′∶B′C′∶C′D′∶D′A′=20∶15∶9∶8,再根据周长是26,即可求得各边长.
解:∵四边形ABCD与四边形A′B′C′D′相似,
∴A′B′∶B′C′∶C′D′∶D′A′=AB∶BC∶CD∶DA=20∶15∶9∶8.
设A′B′=20x,则B′C′=15x,C′D′=9x,D′A′=8x.
∵四边形A′B′C′D′的周长为26,∴20x+15x+9x+8x=26.解得x=0.5,
∴A′B′=10,B′C′=7.5,C′D′=4.5,D′A′=4.
【例4】已知四边形ABCD与四边形A′B′C′D′相似,且AB∶BC∶CD∶DA=20∶15∶9∶8,四边形A′B′C′D′的周长为26,求四边形A′B′C′D′各边的长.
应用二:应用多边形相似的性质解决问题
1.两个多边形相似的条件是( )
A.对应角相等 B.对应边成比例
C.对应角相等或对应边成比例 D.对应角相等且对应边成比例
D
2.下列命题中,正确的是( )
A. 所有的等腰三角形都相似 B. 所有的直角三角形都相似
C. 所有的等边三角形都相似 D. 所有的矩形都相似
C
3.如图所示的两个四边形相似,则∠α的度数是( )
A.87° B.60° C.75° D.120°
A
解:∵两个四边形相似,
∴∠1=138°.
∵四边形的内角和等于360°,
∴∠α=360°﹣60°﹣75°﹣138°=87°,故选A.
4.如图,四边形ABCD的对角线相交于点O,A′、B′、C′、D′分别是OA、OB、OC、OD的中点,试判断四边形ABCD与A′B′C′D′是否相似,并说明理由.
解:相似.其理由是:
由三角形中位线定理可知. ∠B′A′D′=∠BAD,∠A′D′C′=∠ADC,
∠D′C′B′=∠DCB,∠A′B′C′=∠ABC,
∴四边形A′B′C′D′∽四边形ABCD.
相似多边形
各对应角相等、各对应边成比例的两个多边形叫做相似多边形.
相似多边形对应边的比叫做相似比.
在记两个多边形相似时,要把表示对应顶点的字母写在对应的位置上.
相似比与叙述的顺序有关.
相似多边形的对应角相等,对应边成比例.
4.3 相似多边形
1.认识相似图形和相似多边形.
2.会根据条件判断两个多边形是否为相似多边形.
3.掌握相似多边形的性质,能根据性质进行相关的计算.
放大镜下的图形和原来的图形有什么相同与不同吗?
相等.
放大镜下的角与原图形中角是什么关系?
边数不同
角不相等
边成比例
角相等
边不成比例
边成比例
角相等
不相似
不相似
不相似
相似
形状相同的图形叫做相似图形.
小组合作,尝试归纳出相似多边形的概念.
各角分别_______、各边_________的两个多边形叫做相似多边形.
相等
成比例
1.相似多边形:
如图,五边形ABCDE和五边形A′B′C′D′E′形状相同,大小不同.
对应边的比相等: .
对应角相等:, , ,
,
五边形ABCDE 和五边形A′B′C′D′E′相似.
记作: 五边形ABCDE ∽五边形A′B′C′D′E′ ,“∽”读作“相似于”.
观察下列图形,图形(a)~(d)中,与(1)是相似多边形的是哪个?
1.5
3
(c)
边数不同
3
3
(1)
2
2
(b)
(a)
2
2
2
2
(d)
边不成比例
对应角不相等
注意:
两个多边形相似满足的条件:
(1)边数相同;
(2)角分别相等;
(3)边成比例.
以上三者缺一不可.
2.相似比:
相似多边形______________叫做相似比.
对应边的比
3
3
2
2
D1
C1
B1
A1
D
B
C
A
如图,正方形ABCD与正方形A1B1C1D1的相似比为 .
(1)相似比的值与两个多边形的前后顺序有关.
(2)相似比为1的两个相似多边形为全等多边形.
思考:正方形A1B1C1D1与正方形ABCD的相似比是多少?
3.相似多边形的性质:
相似多边形的_______________,__________________.
对应角相等
对应边的比相等
作用:常用来求相似多边形中未知的边的长度和角的度数.
利用相似多边形的性质求边长或角度,关键扣住“对应”二字,找准对应边和对应角是解决问题的关键.
需要注意的是对应边是比相等,而对应角是直接相等.
【例1】 下列四组图形中,一定相似的是( )
A.正方形和矩形 B.正方形和菱形
C.菱形和菱形 D.正方形与正方形
D
A.不一定相似
B.不一定相似
C.不一定相似
D.一定相似
′
′
′
′
【例2】已知:如图,梯形ABCD与梯形A′B′C′D′相似,AD∥BC,
A′D′∥B′C′,∠A=∠A′,AD=4,A′D′=6,AB=6,B′C′=12,∠C=60°.
(1)求梯形ABCD与梯形A′B′C′D′的相似比k的值;
(2)求A′B′和BC的长;
(3)求∠D′的大小.
解 :(1)相似比k=
(2)∵梯形ABCD与梯形A′B′C′D′相似,且由(1)知相似比k=
∴ ∵AB=6,B′C′=12,∴A′B′=9,BC=8.
【例2】已知:如图,梯形ABCD与梯形A′B′C′D′相似,AD∥BC,
A′D′∥B′C′,∠A=∠A′,AD=4,A′D′=6,AB=6,B′C′=12,∠C=60°.
(1)求梯形ABCD与梯形A′B′C′D′的相似比k的值;
(2)求A′B′和BC的长;
(3)求∠D′的大小.
(3)由题意知,∠D′=∠D.
∵AD∥BC,∠C=60°,
∴∠D=180°-∠C=120°. ∴∠D′=120°.
如果两个多边形不相似,那么它们的各角可能对应相等吗?
它们的各边可能对应成比例吗?
观察下面两组图形,图中的两个图形相似吗?为什么?
10
10
8
16
10
10
12
12
不相似
不相似
如果两个多边形不相似,那么它们的各角可能对应相等,它们的各边可能对应成比例.
【例3】如图所示,一块长为2米,宽为1米的矩形玻璃,为了保护玻璃需要镶上宽10厘米的铝合金边框,那么边框的内外边缘所成的矩形相似吗?为什么?
解:不相似. 由条件知, ,,所以.
所以两个矩形不相似.
应用一:判定两个多边形相似
应用二:应用多边形相似的性质解决问题
【例4】已知四边形ABCD与四边形A′B′C′D′相似,且AB∶BC∶CD∶DA=20∶15∶9∶8,四边形A′B′C′D′的周长为26,求四边形A′B′C′D′各边的长.
【分析】已知四边形ABCD与四边形A′B′C′D′相似,且AB∶BC∶CD∶DA=20∶15∶9∶8,则四边形A′B′C′D′的各边A′B′∶B′C′∶C′D′∶D′A′=20∶15∶9∶8,再根据周长是26,即可求得各边长.
解:∵四边形ABCD与四边形A′B′C′D′相似,
∴A′B′∶B′C′∶C′D′∶D′A′=AB∶BC∶CD∶DA=20∶15∶9∶8.
设A′B′=20x,则B′C′=15x,C′D′=9x,D′A′=8x.
∵四边形A′B′C′D′的周长为26,∴20x+15x+9x+8x=26.解得x=0.5,
∴A′B′=10,B′C′=7.5,C′D′=4.5,D′A′=4.
【例4】已知四边形ABCD与四边形A′B′C′D′相似,且AB∶BC∶CD∶DA=20∶15∶9∶8,四边形A′B′C′D′的周长为26,求四边形A′B′C′D′各边的长.
应用二:应用多边形相似的性质解决问题
1.两个多边形相似的条件是( )
A.对应角相等 B.对应边成比例
C.对应角相等或对应边成比例 D.对应角相等且对应边成比例
D
2.下列命题中,正确的是( )
A. 所有的等腰三角形都相似 B. 所有的直角三角形都相似
C. 所有的等边三角形都相似 D. 所有的矩形都相似
C
3.如图所示的两个四边形相似,则∠α的度数是( )
A.87° B.60° C.75° D.120°
A
解:∵两个四边形相似,
∴∠1=138°.
∵四边形的内角和等于360°,
∴∠α=360°﹣60°﹣75°﹣138°=87°,故选A.
4.如图,四边形ABCD的对角线相交于点O,A′、B′、C′、D′分别是OA、OB、OC、OD的中点,试判断四边形ABCD与A′B′C′D′是否相似,并说明理由.
解:相似.其理由是:
由三角形中位线定理可知. ∠B′A′D′=∠BAD,∠A′D′C′=∠ADC,
∠D′C′B′=∠DCB,∠A′B′C′=∠ABC,
∴四边形A′B′C′D′∽四边形ABCD.
相似多边形
各对应角相等、各对应边成比例的两个多边形叫做相似多边形.
相似多边形对应边的比叫做相似比.
在记两个多边形相似时,要把表示对应顶点的字母写在对应的位置上.
相似比与叙述的顺序有关.
相似多边形的对应角相等,对应边成比例.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
