专题8 碰撞-2024高考物理真题分类汇编(全国版 含解析)
文档属性
| 名称 | 专题8 碰撞-2024高考物理真题分类汇编(全国版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-08-08 12:48:41 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2024高考物理真题分项解析
专题08 碰撞
1. (2024高考重庆卷) 如图所示,M、N两个钉子固定于相距a的两点,M的正上方有不可伸长的轻质细绳,一端固定在M上,另一端连接位于M正下方放置于水平地面质量为m的小木块B,绳长与M到地面的距离均为10a,质量为2m的小木块A,沿水平方向于B发生弹性碰撞,碰撞时间极短,A与地面间摩擦因数为,重力加速为g,忽略空气阻力和钉子直径,不计绳被钉子阻挡和绳断裂时的机械能损失。
(1)若碰后,B在竖直面内做圆周运动,且能经过圆周运动最高点,求B碰后瞬间速度的最小值;
(2)若改变A碰前瞬间的速度,碰后A运动到P点停止,B在竖直面圆周运动旋转2圈,经过M正下方时细绳子断开,B也来到P点,求B碰后瞬间的速度大小;
(3)若拉力达到12mg细绳会断,上下移动N的位置,保持N在M正上方,B碰后瞬间的速度与(2)间中的相同,使B旋转n圈。经过M正下的时细绳断开,求MN之间距离的范围,及在n的所有取值中,B落在地面时水平位移的最小值和最大值。
【答案】(1)
(2)
(3)(n = 1,2,3,…),,
【解析】
(1)碰后B能在竖直面内做圆周运动,轨迹半径为10a,设碰后B的最小速度大小为v0,最高点速度大小为v,在最高点时由牛顿第二足定律有
B从最低点到最高点由动能定理可得
解得
(2)A和B碰撞过程中动量守恒,设碰前A的速度大小为v1碰后A的速度大小为v2。碰后B的速度大小为v3,则有
2mv1 = 2mv2+mv3
碰后A减速到0,有
碰后B做两周圆周运动,绳子在MN间缠绕2圈,缩短4a,在M点正下方时,离M点6a,离地面4a,此时速度大小为v4,由功能关系得
B随后做平抛运动,有
L = v4t
解得
(3) 设MN间距离为h,B转n圈后到达M正下方速度大小为v5,绳缩短2nh,绳断开时,以M为圆心,由牛顿第二定律得
(n = 1,2,3,…)
以N为圆心,由牛顿第二定律得
(n = 1,2,3,…)
从碰后到B转n圈后到达M正下方,由功能关系得
(n = 1,2,3,…)
解得
(n = 1,2,3,…)
绳断后,B做平抛运动,有
(n = 1,2,3,…)
s = v5t
可得
(n = 1,2,3,…)
由于
(n = 1,2,3,…)
则由数学分析可得
当时,
当n = 1时,,
2. (2024高考广西卷)如图,在光滑平台上有两个相同的弹性小球M和N。M水平向右运动,速度大小为v。M与静置于平台边缘的N发生正碰,碰撞过程中总机械能守恒。若不计空气阻力,则碰撞后,N在( )
A. 竖直墙面上的垂直投影的运动是匀速运动
B. 竖直增面上的垂直投影的运动是匀加速运动
C. 水平地面上的垂直投影的运动速度大小等于v
D. 水平地面上的垂直投影的运动速度大小大于v
【答案】BC
【解析】
由于两小球碰撞过程中机械能守恒,可知两小球碰撞过程是弹性碰撞,由于两小球质量相等,故碰撞后两小球交换速度,即
,
碰后小球N做平抛运动,在水平方向做匀速直线运动,即水平地面上的垂直投影的运动速度大小等于v;在竖直方向上做自由落体运动,即竖直地面上的垂直投影的运动是匀加速运动。故选BC。
3. (2024年高考广东卷)如图所示,光滑斜坡上,可视为质点的甲、乙两个相同滑块,分别从、高度同时由静止开始下滑。斜坡与水平面在O处平滑相接,滑块与水平面间的动摩擦因数为,乙在水平面上追上甲时发生弹性碰撞。忽略空气阻力。下列说法正确的有( )
A. 甲斜坡上运动时与乙相对静止
B. 碰撞后瞬间甲速度等于碰撞前瞬间乙的速度
C. 乙的运动时间与无关
D. 甲最终停止位置与O处相距
【参考答案】ABD
【名师解析】两滑块在同一斜坡上同时由静止开始下滑,加速度相同,则相对速度为零,即甲斜坡上运动时与乙相对静止,A正确;两物块滑到水平面后均做匀减速直线运动,由于两物块质量相同,且发生弹性碰撞,根据弹性碰撞规律可知碰撞后两滑块交换速度,即 碰撞后瞬间甲速度等于碰撞前瞬间乙的速度,B正确;设斜面倾角为θ,对乙沿斜面下滑,有,在水平面上运动一段时间t2后与甲碰撞,碰撞后以甲碰撞前的速度做匀减速运动,运动时间为t3,乙运动的时间 ,由于t1与H乙有关,则总时间与H乙有关,C错误;一下滑过程,有,由于甲和乙发生弹性碰撞,交换速度,则可知甲最终停止位置与不发生碰撞时乙最终停止位置相同;如果不发生碰撞,乙在水平面上运动最终停止位置,由
联立解得 x=
即发生碰撞后甲最终停止位置与O处相距,D正确。
4. (2024高考甘肃卷) 如图,质量为2kg的小球A(视为质点)在细绳和OP作用下处于平衡状态,细绳,与竖直方向的夹角均为60°。质量为6kg的木板B静止在光滑水平面上,质量为2kg的物块C静止在B的左端。剪断细绳,小球A开始运动。(重力加速度g取)
(1)求A运动到最低点时细绳OP所受的拉力。
(2)A在最低点时,细绳OP断裂。A飞出后恰好与C左侧碰撞(时间极短)、碰后A竖直下落,C水平向右运动。求碰后C的速度大小。
(3)A、C碰后,C相对B滑行4m后与B共速。求C和B之间的动摩擦因数。
【答案】(1);(2);(3)
【解析】
根据题意,设AC质量为,B的质量为,细绳长为,初始时细线与竖直方向夹角。
(1)A开始运动到最低点有
对最低点受力分析,根据牛顿第二定律得
解得
,
(2)A与C相碰时,水平方向动量守恒,由于碰后A竖直下落可知
故解得
(3)A、C碰后,C相对B滑行4m后与B共速,则对CB分析,过程中根据动量守恒可得
根据能量守恒得
联立解得
5. (2024年高考广东卷)汽车的安全带和安全气囊是有效保护乘客的装置。
(1)安全带能通过感应车的加速度自动锁定,其原理的简化模型如图甲所示。在水平路面上刹车的过程中,敏感球由于惯性沿底座斜面上滑直到与车达到共同的加速度a,同时顶起敏感臂,使之处于水平状态,并卡住卷轴外齿轮,锁定安全带。此时敏感臂对敏感球的压力大小为,敏感球的质量为m,重力加速度为g。忽略敏感球受到的摩擦力。求斜面倾角的正切值。
(2)如图乙所示,在安全气囊的性能测试中,可视为质点的头锤从离气囊表面高度为H处做自由落体运动。与正下方的气囊发生碰撞。以头锤到气囊表面为计时起点,气囊对头锤竖直方向作用力F随时间t的变化规律,可近似用图丙所示的图像描述。已知头锤质量,重力加速度大小取。求:
①碰撞过程中F的冲量大小和方向;
②碰撞结束后头锤上升最大高度。
【名师解析】
(1)敏感球受到向下的重力mg、压力FN以及斜面的支持力N,由牛顿第二定律可得
解得
(2)①由图丙的图像面积表示冲量,可知碰撞过程中力F的冲量大小为
方向竖直向上。
②头锤落到气囊上时的速度
与气囊作用过程,取向上方向为正方向,由动量定理,
解得 v=2m/s
则上升的最大高度
6. (2024高考湖南卷)如图,半径为R的圆环水平放置并固定,圆环内有质量为mA和mB的小球A和B(mA>mB)。初始时小球A以初速度v0沿圆环切线方向运动,与静止的小球B发生碰撞。不计小球与圆环之间的摩擦,两小球始终在圆环内运动。
(1)若小球A与B碰撞后结合在一起,求碰撞后小球组合体的速度大小及做圆周运动所需向心力的大小;
(2)若小球A与B之间为弹性碰撞,且所有的碰撞位置刚好位于等边三角形的三个顶点,求小球的质量比。
(3)若小球A与B之间为非弹性碰撞,每次碰撞后的相对速度大小为碰撞前的相对速度大小的e倍(0【答案】(1),;(2)或;
(3)
【解析】
(1)有题意可知A、B系统碰撞前后动量守恒,设碰撞后两小球的速度大小为v,则根据动量守恒有
可得
碰撞后根据牛顿第二定律有
可得
(2)若两球发生弹性碰撞,设碰后速度分别为vA,vB,则碰后动量和能量守恒有
联立解得
,
因为所有的碰撞位置刚好位于等边三角形的三个顶点,如图
①若第二次碰撞发生在图中的b点,则从第一次碰撞到第二次碰撞之间,A、B通过的路程之比为,则有
联立解得
由于两质量均为正数,故k1=0,即
对第二次碰撞,设A、B碰撞后的速度大小分别为,,则同样有
联立解得,,故第三次碰撞发生在b点、第四次碰撞发生在c点,以此类推,满足题意。
②若第二次碰撞发生在图中的c点,则从第一次碰撞到第二次碰撞之间,A、B通过的路程之比为;所以
联立可得
因为两质量均为正数,故k2=0,即
根据①的分析可证,,满足题意。
综上可知
或
(3)第一次碰前相对速度大小为v0,第一次碰后的相对速度大小为,第一次碰后与第二次相碰前B球比A球多运动一圈,即B球相对A球运动一圈,有
第一次碰撞动量守恒有
且
联立解得
B球运动的路程
第二次碰撞的相对速度大小为
第二次碰撞有
且
联立可得
所以B球运动的路程
一共碰了2n次,有
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
2024高考物理真题分项解析
专题08 碰撞
1. (2024高考重庆卷) 如图所示,M、N两个钉子固定于相距a的两点,M的正上方有不可伸长的轻质细绳,一端固定在M上,另一端连接位于M正下方放置于水平地面质量为m的小木块B,绳长与M到地面的距离均为10a,质量为2m的小木块A,沿水平方向于B发生弹性碰撞,碰撞时间极短,A与地面间摩擦因数为,重力加速为g,忽略空气阻力和钉子直径,不计绳被钉子阻挡和绳断裂时的机械能损失。
(1)若碰后,B在竖直面内做圆周运动,且能经过圆周运动最高点,求B碰后瞬间速度的最小值;
(2)若改变A碰前瞬间的速度,碰后A运动到P点停止,B在竖直面圆周运动旋转2圈,经过M正下方时细绳子断开,B也来到P点,求B碰后瞬间的速度大小;
(3)若拉力达到12mg细绳会断,上下移动N的位置,保持N在M正上方,B碰后瞬间的速度与(2)间中的相同,使B旋转n圈。经过M正下的时细绳断开,求MN之间距离的范围,及在n的所有取值中,B落在地面时水平位移的最小值和最大值。
【答案】(1)
(2)
(3)(n = 1,2,3,…),,
【解析】
(1)碰后B能在竖直面内做圆周运动,轨迹半径为10a,设碰后B的最小速度大小为v0,最高点速度大小为v,在最高点时由牛顿第二足定律有
B从最低点到最高点由动能定理可得
解得
(2)A和B碰撞过程中动量守恒,设碰前A的速度大小为v1碰后A的速度大小为v2。碰后B的速度大小为v3,则有
2mv1 = 2mv2+mv3
碰后A减速到0,有
碰后B做两周圆周运动,绳子在MN间缠绕2圈,缩短4a,在M点正下方时,离M点6a,离地面4a,此时速度大小为v4,由功能关系得
B随后做平抛运动,有
L = v4t
解得
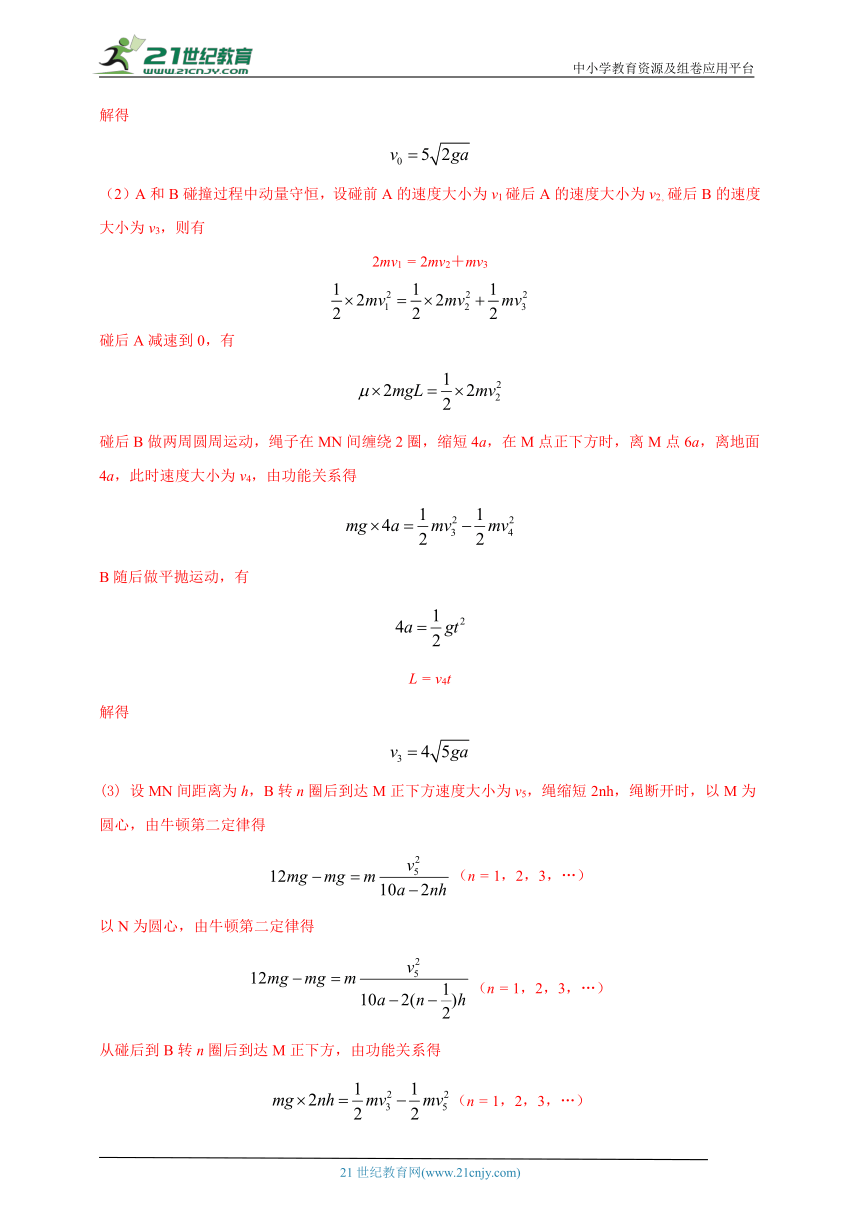
(3) 设MN间距离为h,B转n圈后到达M正下方速度大小为v5,绳缩短2nh,绳断开时,以M为圆心,由牛顿第二定律得
(n = 1,2,3,…)
以N为圆心,由牛顿第二定律得
(n = 1,2,3,…)
从碰后到B转n圈后到达M正下方,由功能关系得
(n = 1,2,3,…)
解得
(n = 1,2,3,…)
绳断后,B做平抛运动,有
(n = 1,2,3,…)
s = v5t
可得
(n = 1,2,3,…)
由于
(n = 1,2,3,…)
则由数学分析可得
当时,
当n = 1时,,
2. (2024高考广西卷)如图,在光滑平台上有两个相同的弹性小球M和N。M水平向右运动,速度大小为v。M与静置于平台边缘的N发生正碰,碰撞过程中总机械能守恒。若不计空气阻力,则碰撞后,N在( )
A. 竖直墙面上的垂直投影的运动是匀速运动
B. 竖直增面上的垂直投影的运动是匀加速运动
C. 水平地面上的垂直投影的运动速度大小等于v
D. 水平地面上的垂直投影的运动速度大小大于v
【答案】BC
【解析】
由于两小球碰撞过程中机械能守恒,可知两小球碰撞过程是弹性碰撞,由于两小球质量相等,故碰撞后两小球交换速度,即
,
碰后小球N做平抛运动,在水平方向做匀速直线运动,即水平地面上的垂直投影的运动速度大小等于v;在竖直方向上做自由落体运动,即竖直地面上的垂直投影的运动是匀加速运动。故选BC。
3. (2024年高考广东卷)如图所示,光滑斜坡上,可视为质点的甲、乙两个相同滑块,分别从、高度同时由静止开始下滑。斜坡与水平面在O处平滑相接,滑块与水平面间的动摩擦因数为,乙在水平面上追上甲时发生弹性碰撞。忽略空气阻力。下列说法正确的有( )
A. 甲斜坡上运动时与乙相对静止
B. 碰撞后瞬间甲速度等于碰撞前瞬间乙的速度
C. 乙的运动时间与无关
D. 甲最终停止位置与O处相距
【参考答案】ABD
【名师解析】两滑块在同一斜坡上同时由静止开始下滑,加速度相同,则相对速度为零,即甲斜坡上运动时与乙相对静止,A正确;两物块滑到水平面后均做匀减速直线运动,由于两物块质量相同,且发生弹性碰撞,根据弹性碰撞规律可知碰撞后两滑块交换速度,即 碰撞后瞬间甲速度等于碰撞前瞬间乙的速度,B正确;设斜面倾角为θ,对乙沿斜面下滑,有,在水平面上运动一段时间t2后与甲碰撞,碰撞后以甲碰撞前的速度做匀减速运动,运动时间为t3,乙运动的时间 ,由于t1与H乙有关,则总时间与H乙有关,C错误;一下滑过程,有,由于甲和乙发生弹性碰撞,交换速度,则可知甲最终停止位置与不发生碰撞时乙最终停止位置相同;如果不发生碰撞,乙在水平面上运动最终停止位置,由
联立解得 x=
即发生碰撞后甲最终停止位置与O处相距,D正确。
4. (2024高考甘肃卷) 如图,质量为2kg的小球A(视为质点)在细绳和OP作用下处于平衡状态,细绳,与竖直方向的夹角均为60°。质量为6kg的木板B静止在光滑水平面上,质量为2kg的物块C静止在B的左端。剪断细绳,小球A开始运动。(重力加速度g取)
(1)求A运动到最低点时细绳OP所受的拉力。
(2)A在最低点时,细绳OP断裂。A飞出后恰好与C左侧碰撞(时间极短)、碰后A竖直下落,C水平向右运动。求碰后C的速度大小。
(3)A、C碰后,C相对B滑行4m后与B共速。求C和B之间的动摩擦因数。
【答案】(1);(2);(3)
【解析】
根据题意,设AC质量为,B的质量为,细绳长为,初始时细线与竖直方向夹角。
(1)A开始运动到最低点有
对最低点受力分析,根据牛顿第二定律得
解得
,
(2)A与C相碰时,水平方向动量守恒,由于碰后A竖直下落可知
故解得
(3)A、C碰后,C相对B滑行4m后与B共速,则对CB分析,过程中根据动量守恒可得
根据能量守恒得
联立解得
5. (2024年高考广东卷)汽车的安全带和安全气囊是有效保护乘客的装置。
(1)安全带能通过感应车的加速度自动锁定,其原理的简化模型如图甲所示。在水平路面上刹车的过程中,敏感球由于惯性沿底座斜面上滑直到与车达到共同的加速度a,同时顶起敏感臂,使之处于水平状态,并卡住卷轴外齿轮,锁定安全带。此时敏感臂对敏感球的压力大小为,敏感球的质量为m,重力加速度为g。忽略敏感球受到的摩擦力。求斜面倾角的正切值。
(2)如图乙所示,在安全气囊的性能测试中,可视为质点的头锤从离气囊表面高度为H处做自由落体运动。与正下方的气囊发生碰撞。以头锤到气囊表面为计时起点,气囊对头锤竖直方向作用力F随时间t的变化规律,可近似用图丙所示的图像描述。已知头锤质量,重力加速度大小取。求:
①碰撞过程中F的冲量大小和方向;
②碰撞结束后头锤上升最大高度。
【名师解析】
(1)敏感球受到向下的重力mg、压力FN以及斜面的支持力N,由牛顿第二定律可得
解得
(2)①由图丙的图像面积表示冲量,可知碰撞过程中力F的冲量大小为
方向竖直向上。
②头锤落到气囊上时的速度
与气囊作用过程,取向上方向为正方向,由动量定理,
解得 v=2m/s
则上升的最大高度
6. (2024高考湖南卷)如图,半径为R的圆环水平放置并固定,圆环内有质量为mA和mB的小球A和B(mA>mB)。初始时小球A以初速度v0沿圆环切线方向运动,与静止的小球B发生碰撞。不计小球与圆环之间的摩擦,两小球始终在圆环内运动。
(1)若小球A与B碰撞后结合在一起,求碰撞后小球组合体的速度大小及做圆周运动所需向心力的大小;
(2)若小球A与B之间为弹性碰撞,且所有的碰撞位置刚好位于等边三角形的三个顶点,求小球的质量比。
(3)若小球A与B之间为非弹性碰撞,每次碰撞后的相对速度大小为碰撞前的相对速度大小的e倍(0
(3)
【解析】
(1)有题意可知A、B系统碰撞前后动量守恒,设碰撞后两小球的速度大小为v,则根据动量守恒有
可得
碰撞后根据牛顿第二定律有
可得
(2)若两球发生弹性碰撞,设碰后速度分别为vA,vB,则碰后动量和能量守恒有
联立解得
,
因为所有的碰撞位置刚好位于等边三角形的三个顶点,如图
①若第二次碰撞发生在图中的b点,则从第一次碰撞到第二次碰撞之间,A、B通过的路程之比为,则有
联立解得
由于两质量均为正数,故k1=0,即
对第二次碰撞,设A、B碰撞后的速度大小分别为,,则同样有
联立解得,,故第三次碰撞发生在b点、第四次碰撞发生在c点,以此类推,满足题意。
②若第二次碰撞发生在图中的c点,则从第一次碰撞到第二次碰撞之间,A、B通过的路程之比为;所以
联立可得
因为两质量均为正数,故k2=0,即
根据①的分析可证,,满足题意。
综上可知
或
(3)第一次碰前相对速度大小为v0,第一次碰后的相对速度大小为,第一次碰后与第二次相碰前B球比A球多运动一圈,即B球相对A球运动一圈,有
第一次碰撞动量守恒有
且
联立解得
B球运动的路程
第二次碰撞的相对速度大小为
第二次碰撞有
且
联立可得
所以B球运动的路程
一共碰了2n次,有
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
