1.1 课时3 菱形的应用 课件 (共18张PPT) 2024-2025学年数学北师版九年级上册
文档属性
| 名称 | 1.1 课时3 菱形的应用 课件 (共18张PPT) 2024-2025学年数学北师版九年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 814.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-07 19:25:41 | ||
图片预览





文档简介
(共18张PPT)
1.1 课时3 菱形的应用
1)掌握菱形面积的特殊计算方法。
2)灵活运用菱形的性质定理与判定定理解决相关问题。
菱形的相关知识有哪些?
菱形 定义
性质
判定
一组邻边相等的平行四边形叫做菱形
具有平行四边形的所有性质
菱形的四条边都相等
对角线互相垂直且平分每一组对角
轴对称图形
一组邻边相等的平行四边形是菱形
四边都相等的四边形是菱形
对角线互相垂直的平行四边形是菱形
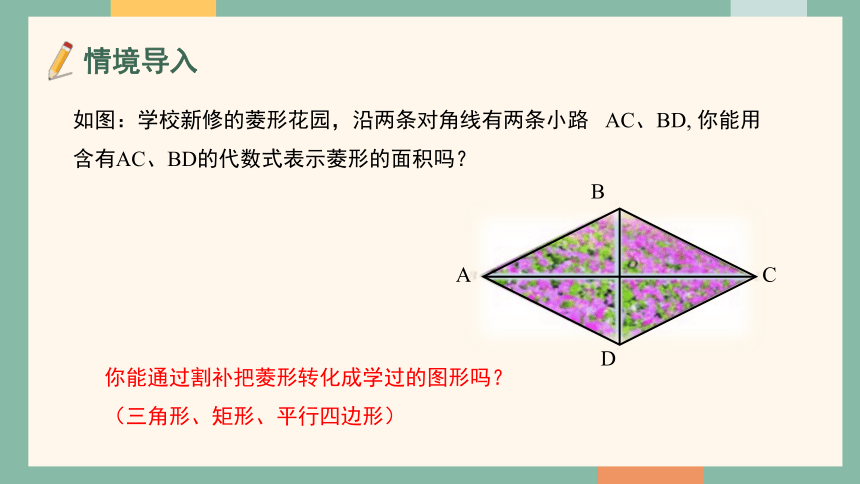
如图:学校新修的菱形花园,沿两条对角线有两条小路 AC、BD, 你能用含有AC、BD的代数式表示菱形的面积吗?
A
B
C
D
你能通过割补把菱形转化成学过的图形吗?
(三角形、矩形、平行四边形)
菱形是特殊的平行四边形,那么能否利用平行四边形面积公式计算菱形ABCD的面积吗
A
B
C
D
能.过点A作AE⊥BC于点E,
则S菱形ABCD=底×高 =BC·AE.
E
思考 前面我们已经学习了菱形的对角线互相垂直,那么能否利用对角线来计算菱形ABCD的面积呢
如图,四边形ABCD是菱形,对角线AC,BD交于点O,试用对角线表示出菱形ABCD的面积.
A
B
C
D
解:因为四边形ABCD是菱形,
所以AC⊥BD,
所以S菱形ABCD=S△ABC +S△ADC
= AC·BO+AC·DO
=AC(BO+DO)
=AC·BD.
你有什么发现?
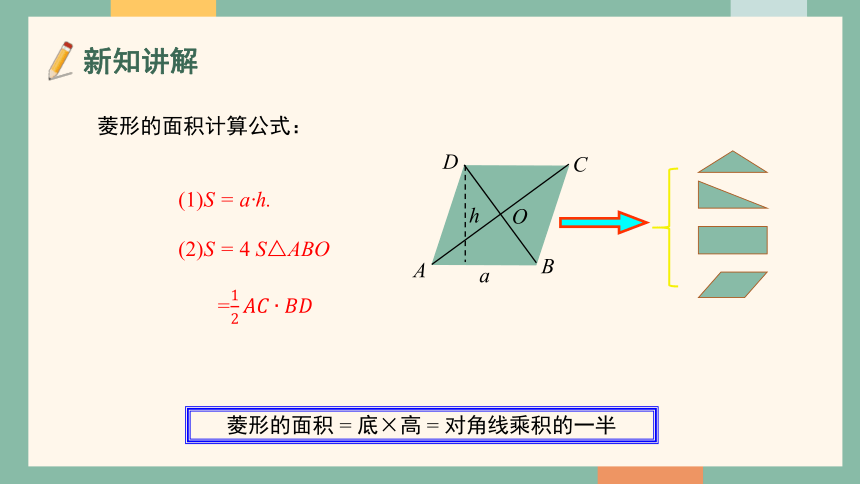
菱形的面积 = 底×高 = 对角线乘积的一半
(1)S = a·h.
(2)S = 4 S△ABO
=
A
B
D
C
a
h
O
菱形的面积 = 底×高 = 对角线乘积的一半
菱形的面积计算公式:
例1.如图,四边形ABCD 是边长为13cm的菱形,其中对角线BD长为10cm.
求:(1)对角线 AC 的长度;
(2)菱形 ABCD 的面积.
(1)解:因为四边形ABCD是菱形,AC与BD相交于点E,
所以AC=2AE=2×12=24(cm)(菱形的对角线互相平分).
所以∠AED=90°(菱形的对角线互相垂直),
DE=BD=×10=5cm(菱形的对角线互相平分),
(2)解:菱形ABCD的面积
=△ABD的面积+△CBD的面积
=2 × △ABD的面积
思考:你还有其他的方法计算菱形的面积吗?
练习:如图所示,在菱形ABCD中,点O为对角线AC与BD的交点,且在△AOB中,AB=13,OA=5,OB=12.求菱形ABCD两对边的距离h.
解:在Rt△AOB中,AB=13,OA=5,OB=12,
于是
所以,S菱形ABCD=4S△AOB=4×30=120.
又因为菱形两组对边的距离相等,
所以,S菱形ABCD=AB h=13h,
即,13h=120,得
例2:在任意四边形ABCD中,对角线AC⊥BD ,且AC=18,BD=10。问四边形ABCD的面积是多少?
D
A
O
B
C
四边形ABCD=S△ABD+S△BCD
S
解:
所以,这个公式对一般的对角线互相垂直的四边形仍成立。
=
=
=
=
练习:两张等宽的纸条交叉重叠在一起,重叠的部分ABCD是 。
菱形
证明:因为 AB//DC,AD//BC
所以四边形ABCD为平行四边形.
过点A、C作AE⊥BC,CF⊥AB,垂足分别为E、F.
则AE=CF,而S四边形ABCD= AB ×CF= BC× AE
所以BC=AB
所以四边形ABCD是菱形.
∟
∟
A
D
B
C
E
F
1.如图,已知AC、BD是菱形ABCD的对角线,那么下列结论一定正确的是( )
A.△ABD与△ABC的周长相等
B.△ABD与△ABC的面积相等
C.菱形的周长等于两条对角线之和的两倍
D.菱形的面积等于两条对角线之积的两倍
B
2.如图,菱形的两条对角线长分别为10cm和24cm,则菱形的边长是( )
A.10cm B.24cm C. 13cm D.17cm
A
B
C
D
O
C
3.如图所示,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF.
(1)求证:四边形BCFE是菱形;
(2)若CE=4,∠BCF=120°,求菱形BCFE的面积.
(1)证明:因为D、E分别是AB、AC的中点,
所以DE∥BC且2DE=BC.
又因为BE=2DE,EF=BE,
所以EF=BC,EF∥BC,
所以四边形BCFE是平行四边形.
又因为EF=BE,所以四边形BCFE是菱形;
(2)解:因为∠BCF=120°,
所以∠EBC=60°,
所以△EBC是等边三角形,
所以菱形的边长为4,高为 ,
所以菱形的面积为4
方法总结:判定一个四边形是菱形时,要结合条件灵活选择方法.如果可以证明四条边相等,可直接证出菱形;如果只能证出一组邻边相等或对角线互相垂直,可以尝试证出这个四边形是平行四边形,然后用定义法或判定定理1来证明菱形.
本节课你学到了什么?
1.菱形的性质与判定的综合性问题
2.菱形的面积
=底×高=两条对角线乘积的一半
3.综合运用
1.1 课时3 菱形的应用
1)掌握菱形面积的特殊计算方法。
2)灵活运用菱形的性质定理与判定定理解决相关问题。
菱形的相关知识有哪些?
菱形 定义
性质
判定
一组邻边相等的平行四边形叫做菱形
具有平行四边形的所有性质
菱形的四条边都相等
对角线互相垂直且平分每一组对角
轴对称图形
一组邻边相等的平行四边形是菱形
四边都相等的四边形是菱形
对角线互相垂直的平行四边形是菱形
如图:学校新修的菱形花园,沿两条对角线有两条小路 AC、BD, 你能用含有AC、BD的代数式表示菱形的面积吗?
A
B
C
D
你能通过割补把菱形转化成学过的图形吗?
(三角形、矩形、平行四边形)
菱形是特殊的平行四边形,那么能否利用平行四边形面积公式计算菱形ABCD的面积吗
A
B
C
D
能.过点A作AE⊥BC于点E,
则S菱形ABCD=底×高 =BC·AE.
E
思考 前面我们已经学习了菱形的对角线互相垂直,那么能否利用对角线来计算菱形ABCD的面积呢
如图,四边形ABCD是菱形,对角线AC,BD交于点O,试用对角线表示出菱形ABCD的面积.
A
B
C
D
解:因为四边形ABCD是菱形,
所以AC⊥BD,
所以S菱形ABCD=S△ABC +S△ADC
= AC·BO+AC·DO
=AC(BO+DO)
=AC·BD.
你有什么发现?
菱形的面积 = 底×高 = 对角线乘积的一半
(1)S = a·h.
(2)S = 4 S△ABO
=
A
B
D
C
a
h
O
菱形的面积 = 底×高 = 对角线乘积的一半
菱形的面积计算公式:
例1.如图,四边形ABCD 是边长为13cm的菱形,其中对角线BD长为10cm.
求:(1)对角线 AC 的长度;
(2)菱形 ABCD 的面积.
(1)解:因为四边形ABCD是菱形,AC与BD相交于点E,
所以AC=2AE=2×12=24(cm)(菱形的对角线互相平分).
所以∠AED=90°(菱形的对角线互相垂直),
DE=BD=×10=5cm(菱形的对角线互相平分),
(2)解:菱形ABCD的面积
=△ABD的面积+△CBD的面积
=2 × △ABD的面积
思考:你还有其他的方法计算菱形的面积吗?
练习:如图所示,在菱形ABCD中,点O为对角线AC与BD的交点,且在△AOB中,AB=13,OA=5,OB=12.求菱形ABCD两对边的距离h.
解:在Rt△AOB中,AB=13,OA=5,OB=12,
于是
所以,S菱形ABCD=4S△AOB=4×30=120.
又因为菱形两组对边的距离相等,
所以,S菱形ABCD=AB h=13h,
即,13h=120,得
例2:在任意四边形ABCD中,对角线AC⊥BD ,且AC=18,BD=10。问四边形ABCD的面积是多少?
D
A
O
B
C
四边形ABCD=S△ABD+S△BCD
S
解:
所以,这个公式对一般的对角线互相垂直的四边形仍成立。
=
=
=
=
练习:两张等宽的纸条交叉重叠在一起,重叠的部分ABCD是 。
菱形
证明:因为 AB//DC,AD//BC
所以四边形ABCD为平行四边形.
过点A、C作AE⊥BC,CF⊥AB,垂足分别为E、F.
则AE=CF,而S四边形ABCD= AB ×CF= BC× AE
所以BC=AB
所以四边形ABCD是菱形.
∟
∟
A
D
B
C
E
F
1.如图,已知AC、BD是菱形ABCD的对角线,那么下列结论一定正确的是( )
A.△ABD与△ABC的周长相等
B.△ABD与△ABC的面积相等
C.菱形的周长等于两条对角线之和的两倍
D.菱形的面积等于两条对角线之积的两倍
B
2.如图,菱形的两条对角线长分别为10cm和24cm,则菱形的边长是( )
A.10cm B.24cm C. 13cm D.17cm
A
B
C
D
O
C
3.如图所示,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF.
(1)求证:四边形BCFE是菱形;
(2)若CE=4,∠BCF=120°,求菱形BCFE的面积.
(1)证明:因为D、E分别是AB、AC的中点,
所以DE∥BC且2DE=BC.
又因为BE=2DE,EF=BE,
所以EF=BC,EF∥BC,
所以四边形BCFE是平行四边形.
又因为EF=BE,所以四边形BCFE是菱形;
(2)解:因为∠BCF=120°,
所以∠EBC=60°,
所以△EBC是等边三角形,
所以菱形的边长为4,高为 ,
所以菱形的面积为4
方法总结:判定一个四边形是菱形时,要结合条件灵活选择方法.如果可以证明四条边相等,可直接证出菱形;如果只能证出一组邻边相等或对角线互相垂直,可以尝试证出这个四边形是平行四边形,然后用定义法或判定定理1来证明菱形.
本节课你学到了什么?
1.菱形的性质与判定的综合性问题
2.菱形的面积
=底×高=两条对角线乘积的一半
3.综合运用
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
