2.1 课时2 一元二次方程根的估算 课件 (共17张PPT) 2024-2025学年数学北师版九年级上册
文档属性
| 名称 | 2.1 课时2 一元二次方程根的估算 课件 (共17张PPT) 2024-2025学年数学北师版九年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-07 19:38:01 | ||
图片预览





文档简介
(共17张PPT)
2.1 课时2 一元二次方程根的估算
1.理解方程解的概念.
2.经历对一元二次方程解的探索过程能理解其意义.
3.会利用“两边夹”的思想估算一元二次方程的解.
1. 使方程左右两边相等的未知数的值叫做方程的______.
一元二次方程 (x+1)2 - x = 3(x2-2) 化成一般形式是
__________________.
3. 近似数 2.36 ≈ _______(精确到0.1).
解
2x2–x -7 = 0
2.4
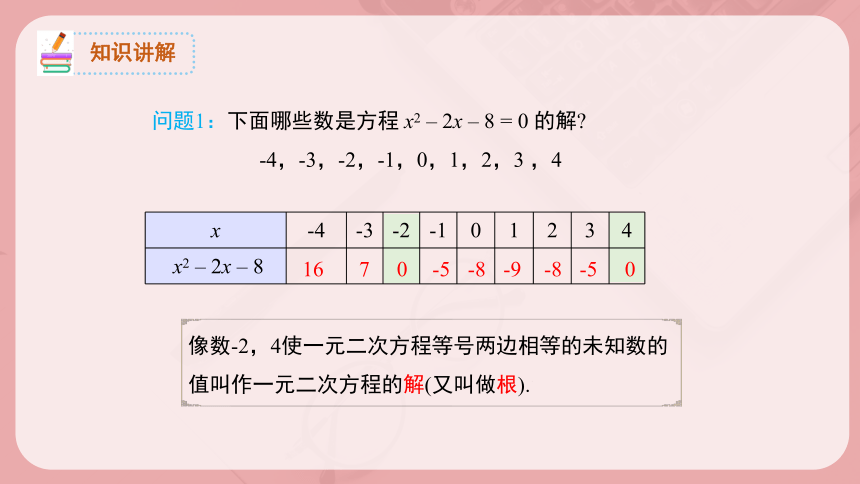
问题1:下面哪些数是方程 x2 – 2x – 8 = 0 的解
-4,-3,-2,-1,0,1,2,3 ,4
x -4 -3 -2 -1 0 1 2 3 4
x2 – 2x – 8
16
-8
7
0
-5
-8
-9
-5
0
像数-2,4使一元二次方程等号两边相等的未知数的
值叫作一元二次方程的解(又叫做根).
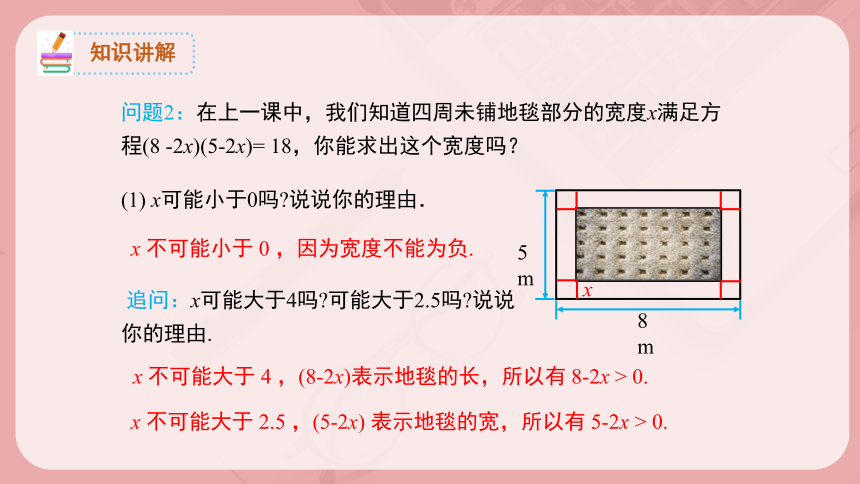
问题2:在上一课中,我们知道四周未铺地毯部分的宽度x满足方程(8 -2x)(5-2x)= 18,你能求出这个宽度吗?
8 m
5 m
(1) x可能小于0吗 说说你的理由.
追问:x可能大于4吗 可能大于2.5吗 说说你的理由.
x
x 不可能小于 0 ,因为宽度不能为负.
x 不可能大于 4 ,(8-2x)表示地毯的长,所以有 8-2x > 0.
x 不可能大于 2.5 ,(5-2x) 表示地毯的宽,所以有 5-2x > 0.
问题2:在上一课中,我们知道四周未铺地毯部分的宽度x满足方程(8 -2x)(5-2x)= 18,你能求出这个宽度吗?
8 m
5 m
(2) 你能确定 x 的大致范围吗?
x
由(1)可知:0(3) 填写下表:
x 0.5 1 1.5 2
(8-2x)(5-2x)
(4) 你知道地毯花边的宽 x(m) 是多少吗?
所求宽度为 1 m.
28
18
10
4
你还有其他求解方法吗?
问题3:在上一课中,梯子的底端滑动的距离x满足方程72+(x+6)2 = 102 ,也就是x2 +12 x - 15 = 0.
10m
8m
1m
xm
(1) 小明认为底端也滑动了 1 m,他的说法正确吗?为什么?
不正确,因为 x = 1时不满足方程.
(2) 底端滑动的距离可能是 2 m 吗?可能是
3 m 吗?为什么?
不可能是 2 ,因为 x = 2 时不满足方程.
不可能是 3 ,因为 x = 3 时不满足方程.
问题3:在上一课中,梯子的底端滑动的距离x满足方程72+(x+6)2 = 102 ,也就是x2 +12 x - 15 = 0.
10m
8m
1m
xm
(3)你能猜出滑动距离 x(m) 的大致范围吗?
x 1 2 3
x2 +12 x - 15
-2
13
30
猜测:1问题3:在上一课中,梯子的底端滑动的距离x满足方程72+(x+6)2 = 102 ,也就是x2 +12 x - 15 = 0.
(4)由(3)可知x的整数部分是1,那它的十分位是几?
x 0 0.5 1 1.5 2
x2 + 12x - 15
-15
-8.75
-2
5.25
13
下面是小亮的求解过程:
可知x取值的大致范围是:1x 1.0 1.1 1.2 1.3 1.4
x2 + 12x - 15
-0.59
0.84
2.29
3.76
-2
所以1.1<x<1.2,因此x整数部分是1,十分位部分是1.
你的结果是怎样的?
进一步计算:
上述求解是利用了“两边夹”的思想
用“两边夹”思想解一元二次方程的步骤:
①在未知数x的取值范围内排除一部分取值;
②再次进行排除,取值范围确定在两个连续整数之间;
③对列出能反映未知数和方程的值的表格进行再次筛选;
④最终得出未知数的最小取值范围或具体数据.
例 请估算出一元二次方程 x2 - 2x - 1=0的正数根(精确到0.1).
①先列表确定整数部分,当2<x<3时,-1< x2 -2x -1<2,则正数根在2到3之间;
②再列表确定十分位部分,当2.4<x<2.5时,-0.04< x2 -2x -1<0.25,则正数根在2.4到2.5之间;
③最后确定百分位部分,当x=2.45时, x2 -2x -1的值是否大于0,若大于0,则正数根在2.4到2.45之间;若小于0,则正数根在2.45到2.50之间.再根据精确到0.1,四舍五入取值即可.
分析:
例 请估算出一元二次方程 x2 - 2x - 1=0的正数根(精确到0.1).
解:(1)列表.依次取x=0,1,2 ,3…
x 0 1 2 3 ...
x2 - 2x -1 -1 -2 -1 2 ...
由上表可发现,当2<x<3时, -1< x2 - 2x -1 <2;
(2)继续列表,依次取x=2.1,2.2,2.3,2.4,2.5…
由表发现,当2.4<x<2.5时,-0.04< x2 -2x-1<0.25;
(3)取x=2.45,则x2 - 2x - 1≈0.1025.
∴2.4<x<2.45.∴x≈2.4,即正数根为2.4.
x 2.1 2.2 2.3 2.4 2.5 ...
x2 - 2x -1 -0.79 -0.56 -0.31 -0.04 0.25 ...
1.五个连续整数,前三个数的平方和等于后两个数的平方.您能求出这五个整数分别是多少吗?
解: 设第一个整数为 x.
x2+(x+1)2+(x+2)2 = (x+3)2+(x+4)2.
3x2+6x+5 = 2x2+14x+25.
x2-8x-20=0.
列表:
x -3 -2 -1 ... 9 10 11
x2 - 8x -20 13 0 -11 ... -11 0 13
所以x=-2或10.
所以,这五个整数分别是10,11,12,13,14 或 -2,-1,0,1,2.
2.根据题意,列出方程,并估算方程的解:一个面积为 120 m2 的矩形苗圃,它的长比宽多 2 m. 苗圃的长和宽各是多少?
解:设苗圃的宽为x m,则长为(x+2) m ,根据题意,得: x(x + 2) = 120.
即 x2 + 2x - 120 = 0.
列表:
x 8 9 10 11 12
x2 +2x -120 -40 -21 0 23 48
所以,苗圃的宽为 10 m,长为 12 m.
3.有一条长为 16 m 的绳子,你能否用它围出一个面积为 15 m2 的矩形?若能,则矩形的长、宽各是多少?
解: 能,设矩形的宽为 x m,则长为(8-x)m.
依题意,得x(8-x) = 15.
即:x2-8x+15= 0.
列表:
所以,矩形的宽为 3 m,长为 5 m.
x 1 2 3 4
x2 -8x +15 8 3 0 -1
用“两边夹”思想估算一元二次方程解的一般步骤:
一元二次方程的解及其估算
一元二次方程的解:
使一元二次方程等号两边相等的未知数的
值叫作一元二次方程的解(又叫做根).
①在未知数x的取值范围内排除一部分取值;
②再次进行排除,取值范围确定在两个连续整数之间;
③对列出能反映未知数和方程的值的表格进行再次筛选;
④最终得出未知数的最小取值范围或具体数据.
2.1 课时2 一元二次方程根的估算
1.理解方程解的概念.
2.经历对一元二次方程解的探索过程能理解其意义.
3.会利用“两边夹”的思想估算一元二次方程的解.
1. 使方程左右两边相等的未知数的值叫做方程的______.
一元二次方程 (x+1)2 - x = 3(x2-2) 化成一般形式是
__________________.
3. 近似数 2.36 ≈ _______(精确到0.1).
解
2x2–x -7 = 0
2.4
问题1:下面哪些数是方程 x2 – 2x – 8 = 0 的解
-4,-3,-2,-1,0,1,2,3 ,4
x -4 -3 -2 -1 0 1 2 3 4
x2 – 2x – 8
16
-8
7
0
-5
-8
-9
-5
0
像数-2,4使一元二次方程等号两边相等的未知数的
值叫作一元二次方程的解(又叫做根).
问题2:在上一课中,我们知道四周未铺地毯部分的宽度x满足方程(8 -2x)(5-2x)= 18,你能求出这个宽度吗?
8 m
5 m
(1) x可能小于0吗 说说你的理由.
追问:x可能大于4吗 可能大于2.5吗 说说你的理由.
x
x 不可能小于 0 ,因为宽度不能为负.
x 不可能大于 4 ,(8-2x)表示地毯的长,所以有 8-2x > 0.
x 不可能大于 2.5 ,(5-2x) 表示地毯的宽,所以有 5-2x > 0.
问题2:在上一课中,我们知道四周未铺地毯部分的宽度x满足方程(8 -2x)(5-2x)= 18,你能求出这个宽度吗?
8 m
5 m
(2) 你能确定 x 的大致范围吗?
x
由(1)可知:0
x 0.5 1 1.5 2
(8-2x)(5-2x)
(4) 你知道地毯花边的宽 x(m) 是多少吗?
所求宽度为 1 m.
28
18
10
4
你还有其他求解方法吗?
问题3:在上一课中,梯子的底端滑动的距离x满足方程72+(x+6)2 = 102 ,也就是x2 +12 x - 15 = 0.
10m
8m
1m
xm
(1) 小明认为底端也滑动了 1 m,他的说法正确吗?为什么?
不正确,因为 x = 1时不满足方程.
(2) 底端滑动的距离可能是 2 m 吗?可能是
3 m 吗?为什么?
不可能是 2 ,因为 x = 2 时不满足方程.
不可能是 3 ,因为 x = 3 时不满足方程.
问题3:在上一课中,梯子的底端滑动的距离x满足方程72+(x+6)2 = 102 ,也就是x2 +12 x - 15 = 0.
10m
8m
1m
xm
(3)你能猜出滑动距离 x(m) 的大致范围吗?
x 1 2 3
x2 +12 x - 15
-2
13
30
猜测:1
(4)由(3)可知x的整数部分是1,那它的十分位是几?
x 0 0.5 1 1.5 2
x2 + 12x - 15
-15
-8.75
-2
5.25
13
下面是小亮的求解过程:
可知x取值的大致范围是:1
x2 + 12x - 15
-0.59
0.84
2.29
3.76
-2
所以1.1<x<1.2,因此x整数部分是1,十分位部分是1.
你的结果是怎样的?
进一步计算:
上述求解是利用了“两边夹”的思想
用“两边夹”思想解一元二次方程的步骤:
①在未知数x的取值范围内排除一部分取值;
②再次进行排除,取值范围确定在两个连续整数之间;
③对列出能反映未知数和方程的值的表格进行再次筛选;
④最终得出未知数的最小取值范围或具体数据.
例 请估算出一元二次方程 x2 - 2x - 1=0的正数根(精确到0.1).
①先列表确定整数部分,当2<x<3时,-1< x2 -2x -1<2,则正数根在2到3之间;
②再列表确定十分位部分,当2.4<x<2.5时,-0.04< x2 -2x -1<0.25,则正数根在2.4到2.5之间;
③最后确定百分位部分,当x=2.45时, x2 -2x -1的值是否大于0,若大于0,则正数根在2.4到2.45之间;若小于0,则正数根在2.45到2.50之间.再根据精确到0.1,四舍五入取值即可.
分析:
例 请估算出一元二次方程 x2 - 2x - 1=0的正数根(精确到0.1).
解:(1)列表.依次取x=0,1,2 ,3…
x 0 1 2 3 ...
x2 - 2x -1 -1 -2 -1 2 ...
由上表可发现,当2<x<3时, -1< x2 - 2x -1 <2;
(2)继续列表,依次取x=2.1,2.2,2.3,2.4,2.5…
由表发现,当2.4<x<2.5时,-0.04< x2 -2x-1<0.25;
(3)取x=2.45,则x2 - 2x - 1≈0.1025.
∴2.4<x<2.45.∴x≈2.4,即正数根为2.4.
x 2.1 2.2 2.3 2.4 2.5 ...
x2 - 2x -1 -0.79 -0.56 -0.31 -0.04 0.25 ...
1.五个连续整数,前三个数的平方和等于后两个数的平方.您能求出这五个整数分别是多少吗?
解: 设第一个整数为 x.
x2+(x+1)2+(x+2)2 = (x+3)2+(x+4)2.
3x2+6x+5 = 2x2+14x+25.
x2-8x-20=0.
列表:
x -3 -2 -1 ... 9 10 11
x2 - 8x -20 13 0 -11 ... -11 0 13
所以x=-2或10.
所以,这五个整数分别是10,11,12,13,14 或 -2,-1,0,1,2.
2.根据题意,列出方程,并估算方程的解:一个面积为 120 m2 的矩形苗圃,它的长比宽多 2 m. 苗圃的长和宽各是多少?
解:设苗圃的宽为x m,则长为(x+2) m ,根据题意,得: x(x + 2) = 120.
即 x2 + 2x - 120 = 0.
列表:
x 8 9 10 11 12
x2 +2x -120 -40 -21 0 23 48
所以,苗圃的宽为 10 m,长为 12 m.
3.有一条长为 16 m 的绳子,你能否用它围出一个面积为 15 m2 的矩形?若能,则矩形的长、宽各是多少?
解: 能,设矩形的宽为 x m,则长为(8-x)m.
依题意,得x(8-x) = 15.
即:x2-8x+15= 0.
列表:
所以,矩形的宽为 3 m,长为 5 m.
x 1 2 3 4
x2 -8x +15 8 3 0 -1
用“两边夹”思想估算一元二次方程解的一般步骤:
一元二次方程的解及其估算
一元二次方程的解:
使一元二次方程等号两边相等的未知数的
值叫作一元二次方程的解(又叫做根).
①在未知数x的取值范围内排除一部分取值;
②再次进行排除,取值范围确定在两个连续整数之间;
③对列出能反映未知数和方程的值的表格进行再次筛选;
④最终得出未知数的最小取值范围或具体数据.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
