1.3 课时1 正方形的性质 课件 (共19张PPT) 2024-2025学年数学北师版九年级上册
文档属性
| 名称 | 1.3 课时1 正方形的性质 课件 (共19张PPT) 2024-2025学年数学北师版九年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 8.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-07 00:00:00 | ||
图片预览



文档简介
(共19张PPT)
1.3 课时1
正方形的性质
1.理解正方形的定义,了解正方形与平行四边形、矩形、菱形之间的联系和区别.
2.掌握正方形的性质定理,并会进行有关的计算与证明.
观察下面图形,正方形是我们熟悉的几何图形,在生活中无处不在.
你还能举出其他的例子吗?
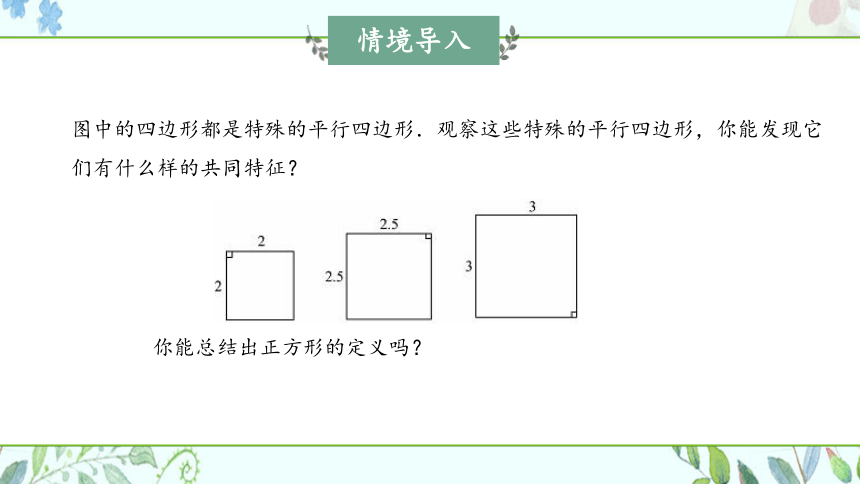
图中的四边形都是特殊的平行四边形.观察这些特殊的平行四边形,你能发现它们有什么样的共同特征?
你能总结出正方形的定义吗?
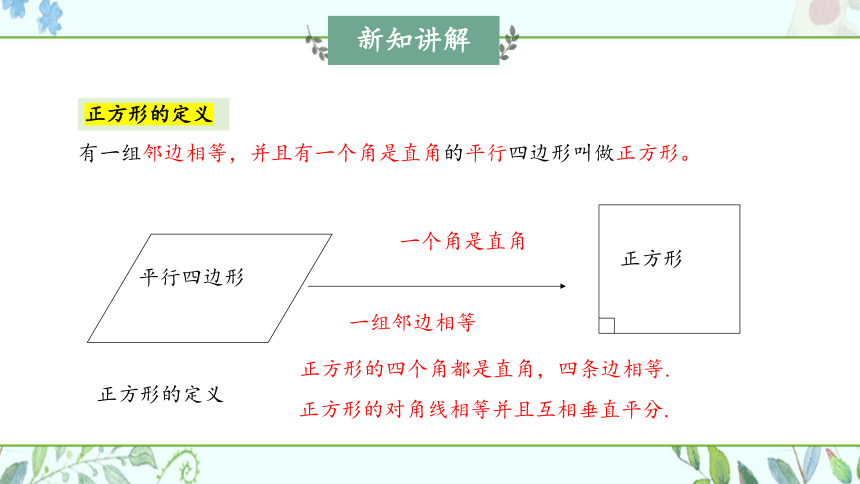
正方形的定义
有一组邻边相等,并且有一个角是直角的平行四边形叫做正方形。
平行四边形
一组邻边相等
一个角是直角
正方形
正方形的对角线相等并且互相垂直平分.
正方形的四个角都是直角,四条边相等.
正方形的定义
A
B
C
D
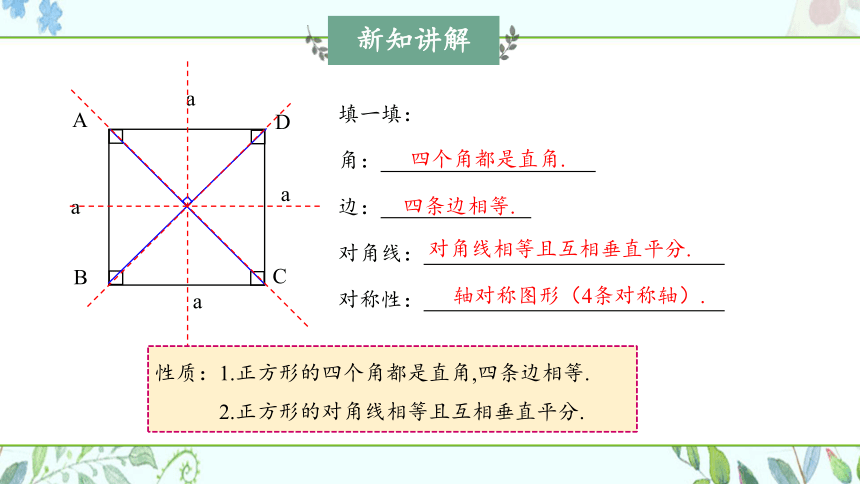
填一填:
角:
边:
对角线:
对称性:
四个角都是直角.
四条边相等.
对角线相等且互相垂直平分.
a
a
a
a
轴对称图形(4条对称轴).
性质:1.正方形的四个角都是直角,四条边相等.
2.正方形的对角线相等且互相垂直平分.
已知:如图,四边形ABCD是正方形.
求证:正方形ABCD四边相等,四个角都是直角.
A
B
C
D
证明:∵四边形ABCD是正方形.
∴∠A=90°, AB=AC (正方形的定义).
又∵正方形是平行四边形.
∴正方形是矩形(矩形的定义),
正方形是菱形(菱形的定义).
∴∠A=∠B =∠C =∠D = 90°, AB= BC=CD=AD.
定理1:正方形的四个角都是直角,四条边相等.
已知:如图,四边形ABCD是正方形.对角线AC、BD相交于点O.求证:AO=BO=CO=DO,AC⊥BD.
A
B
C
D
O
证明:∵正方形ABCD是矩形,
∴AO=BO=CO=DO.
∵正方形ABCD是菱形.
∴AC⊥BD.
正方形的性质
定理2:正方形的对角线相等并且互相垂直平分.
正方形
对角线
边
边
对角线
对角线
角
对边平行且相等
相互平分
相等
四个角相等都是90°
相互垂直且
平分对角
四边相等
对称性
轴对称图形(4条对称轴)
例1.如图,在正方形 ABCD 中,E 为 CD 上一点,F 为BC 边延长线上一点,且 CE = CF. BE 与 DF 之间有怎样的关系?请说明理由.
解:BE = DF, 且 BE⊥DF. 理由如下:
(1)∵四边形 ABCD 是正方形.
∴BC = DC,∠BCE = 90°(正方形的四条边都相等,四个角都是直角).
∴∠DCF = 180°-∠BCE = 180°-90°= 90°.
∴∠BCE =∠DCF.
又∵CE = CF.
∴△BCE≌△DCF. ∴BE = DF.
(2)延长BE交DF于点M(如图).
∵△BCE≌△DCF,
∴∠CBE=∠CDF.
∵∠DCF=90°,
∴∠CDF+∠F=90°.
∴∠CBE+∠F=90°.
∴∠BMF=90°. ∴BE⊥DF.
平行四边形、菱形、矩形、正方形之间有么关系?你能用一个你喜欢的方式直观地示它们之间的关系吗?与同伴交流.
平行四边形
矩形
菱形
正方形
正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形.所以矩形、菱形有的性质,正方形都有.
例2.如图,在正方形ABCD中,E 为CD 上一点,F 为BC 延长线上一点,CE =CF.
(1)求证:△BCE ≌△DCF;
(2)若∠BEC =60°,求∠EFD 的度数.
(1)证明:∵四边形ABCD 是正方形,
∴ BC=DC,∠BCE =∠DCF =90° .
又∵ CE=CF,
∴△BCE ≌△DCF.
(2)解:∵△ BCE ≌△ DCF,∠ BEC=60°,
∴∠ DFC= ∠ BEC=60° .
∵ CE=CF,∠ ECF=90°,
∴∠ CFE=45° .
∴∠ EFD=∠ DFC- ∠ CFE=60°-45°=15°.
例3.如图,在正方形ABCD中,ΔBEC是等边三角形,
求证:∠EAD=∠EDA=15° .
证明:∵ ΔBEC是等边三角形,
∴BE=CE=BC,∠EBC=∠ECB=60°,
∵ 四边形ABCD是正方形,
∴AB=BC=CD,∠ABC=∠DCB=90°,
∴AB=BE=CE=CD, ∠ABE=∠DCE=30°,
∴△ABE,△DCE是等腰三角形,
∴∠BAE=∠BEA=∠CDE=∠CED=75°,
∴∠EAD=∠EDA=90°-75°=15°.
1.平行四边形、矩形、菱形、正方形都具有的是( )
A.对角线互相平分 B.对角线互相垂直
C.对角线相等 D.对角线互相垂直且相等
A
2.一个正方形的对角线长为2cm,则它的面积是 .
2cm
3.如图,正方形ABCD的边长为1cm,AC为对角线,AE平分∠BAC,EF⊥AC,(1)求证:BE=CF;(2)求BE的长.
(1)证明:∵四边形ABCD为正方形,∴AB=BC,
∴∠B=90°,∠ACB=45°,AB=BC=1cm.
∵AE平分∠BAC,EB⊥AB,EF⊥AC,
∴△ABE≌△AFE(AAS),∴BE=EF,∠EFA=∠EFC=90°.
又∵∠ACB=45°,
∴△EFC是等腰直角三角形,∴EF=FC.
∴BE=FC.
3.如图,正方形ABCD的边长为1cm,AC为对角线,AE平分∠BAC,EF⊥AC,(2)求BE的长.
(2)解:由(1)得△ABE≌△AFE,
∴AB=AF=1cm,
在Rt△ABC中,
∴BE=CF=AC-AF=
正方形的定义及性质
正方形的四个角都是直角,四条边相等.
正方形的对角线相等并且互相垂直平分.
一组邻边相等,并且有一个角是直角的平行四边形叫做正方形.
正方形的定义:
正方形的性质:
1.3 课时1
正方形的性质
1.理解正方形的定义,了解正方形与平行四边形、矩形、菱形之间的联系和区别.
2.掌握正方形的性质定理,并会进行有关的计算与证明.
观察下面图形,正方形是我们熟悉的几何图形,在生活中无处不在.
你还能举出其他的例子吗?
图中的四边形都是特殊的平行四边形.观察这些特殊的平行四边形,你能发现它们有什么样的共同特征?
你能总结出正方形的定义吗?
正方形的定义
有一组邻边相等,并且有一个角是直角的平行四边形叫做正方形。
平行四边形
一组邻边相等
一个角是直角
正方形
正方形的对角线相等并且互相垂直平分.
正方形的四个角都是直角,四条边相等.
正方形的定义
A
B
C
D
填一填:
角:
边:
对角线:
对称性:
四个角都是直角.
四条边相等.
对角线相等且互相垂直平分.
a
a
a
a
轴对称图形(4条对称轴).
性质:1.正方形的四个角都是直角,四条边相等.
2.正方形的对角线相等且互相垂直平分.
已知:如图,四边形ABCD是正方形.
求证:正方形ABCD四边相等,四个角都是直角.
A
B
C
D
证明:∵四边形ABCD是正方形.
∴∠A=90°, AB=AC (正方形的定义).
又∵正方形是平行四边形.
∴正方形是矩形(矩形的定义),
正方形是菱形(菱形的定义).
∴∠A=∠B =∠C =∠D = 90°, AB= BC=CD=AD.
定理1:正方形的四个角都是直角,四条边相等.
已知:如图,四边形ABCD是正方形.对角线AC、BD相交于点O.求证:AO=BO=CO=DO,AC⊥BD.
A
B
C
D
O
证明:∵正方形ABCD是矩形,
∴AO=BO=CO=DO.
∵正方形ABCD是菱形.
∴AC⊥BD.
正方形的性质
定理2:正方形的对角线相等并且互相垂直平分.
正方形
对角线
边
边
对角线
对角线
角
对边平行且相等
相互平分
相等
四个角相等都是90°
相互垂直且
平分对角
四边相等
对称性
轴对称图形(4条对称轴)
例1.如图,在正方形 ABCD 中,E 为 CD 上一点,F 为BC 边延长线上一点,且 CE = CF. BE 与 DF 之间有怎样的关系?请说明理由.
解:BE = DF, 且 BE⊥DF. 理由如下:
(1)∵四边形 ABCD 是正方形.
∴BC = DC,∠BCE = 90°(正方形的四条边都相等,四个角都是直角).
∴∠DCF = 180°-∠BCE = 180°-90°= 90°.
∴∠BCE =∠DCF.
又∵CE = CF.
∴△BCE≌△DCF. ∴BE = DF.
(2)延长BE交DF于点M(如图).
∵△BCE≌△DCF,
∴∠CBE=∠CDF.
∵∠DCF=90°,
∴∠CDF+∠F=90°.
∴∠CBE+∠F=90°.
∴∠BMF=90°. ∴BE⊥DF.
平行四边形、菱形、矩形、正方形之间有么关系?你能用一个你喜欢的方式直观地示它们之间的关系吗?与同伴交流.
平行四边形
矩形
菱形
正方形
正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形.所以矩形、菱形有的性质,正方形都有.
例2.如图,在正方形ABCD中,E 为CD 上一点,F 为BC 延长线上一点,CE =CF.
(1)求证:△BCE ≌△DCF;
(2)若∠BEC =60°,求∠EFD 的度数.
(1)证明:∵四边形ABCD 是正方形,
∴ BC=DC,∠BCE =∠DCF =90° .
又∵ CE=CF,
∴△BCE ≌△DCF.
(2)解:∵△ BCE ≌△ DCF,∠ BEC=60°,
∴∠ DFC= ∠ BEC=60° .
∵ CE=CF,∠ ECF=90°,
∴∠ CFE=45° .
∴∠ EFD=∠ DFC- ∠ CFE=60°-45°=15°.
例3.如图,在正方形ABCD中,ΔBEC是等边三角形,
求证:∠EAD=∠EDA=15° .
证明:∵ ΔBEC是等边三角形,
∴BE=CE=BC,∠EBC=∠ECB=60°,
∵ 四边形ABCD是正方形,
∴AB=BC=CD,∠ABC=∠DCB=90°,
∴AB=BE=CE=CD, ∠ABE=∠DCE=30°,
∴△ABE,△DCE是等腰三角形,
∴∠BAE=∠BEA=∠CDE=∠CED=75°,
∴∠EAD=∠EDA=90°-75°=15°.
1.平行四边形、矩形、菱形、正方形都具有的是( )
A.对角线互相平分 B.对角线互相垂直
C.对角线相等 D.对角线互相垂直且相等
A
2.一个正方形的对角线长为2cm,则它的面积是 .
2cm
3.如图,正方形ABCD的边长为1cm,AC为对角线,AE平分∠BAC,EF⊥AC,(1)求证:BE=CF;(2)求BE的长.
(1)证明:∵四边形ABCD为正方形,∴AB=BC,
∴∠B=90°,∠ACB=45°,AB=BC=1cm.
∵AE平分∠BAC,EB⊥AB,EF⊥AC,
∴△ABE≌△AFE(AAS),∴BE=EF,∠EFA=∠EFC=90°.
又∵∠ACB=45°,
∴△EFC是等腰直角三角形,∴EF=FC.
∴BE=FC.
3.如图,正方形ABCD的边长为1cm,AC为对角线,AE平分∠BAC,EF⊥AC,(2)求BE的长.
(2)解:由(1)得△ABE≌△AFE,
∴AB=AF=1cm,
在Rt△ABC中,
∴BE=CF=AC-AF=
正方形的定义及性质
正方形的四个角都是直角,四条边相等.
正方形的对角线相等并且互相垂直平分.
一组邻边相等,并且有一个角是直角的平行四边形叫做正方形.
正方形的定义:
正方形的性质:
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
