3.1 课时3 用树状图或表格分析配紫色游戏的概率 课件 (共17张PPT) 2024-2025学年数学北师版九年级上册
文档属性
| 名称 | 3.1 课时3 用树状图或表格分析配紫色游戏的概率 课件 (共17张PPT) 2024-2025学年数学北师版九年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-07 00:00:00 | ||
图片预览



文档简介
(共17张PPT)
3.1 课时3 用树状图或
表格分析配紫色游戏的概率
1.通过配色游戏,进一步体会用树状图、表格法计算概率;
2.用树状图和表格法计算随机事件发生的概率.
3.在利用树状图或者列表法求概率时,各种情况出现可能性不同时的情况处理.
B盘
A盘
红
蓝
白
黄
绿
B盘
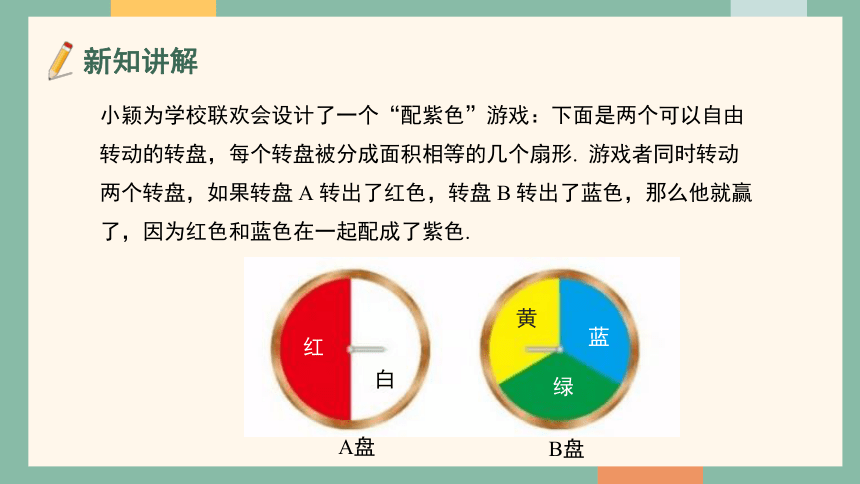
小颖为学校联欢会设计了一个“配紫色”游戏:下面是两个可以自由转动的转盘,每个转盘被分成面积相等的几个扇形. 游戏者同时转动两个转盘,如果转盘 A 转出了红色,转盘 B 转出了蓝色,那么他就赢了,因为红色和蓝色在一起配成了紫色.
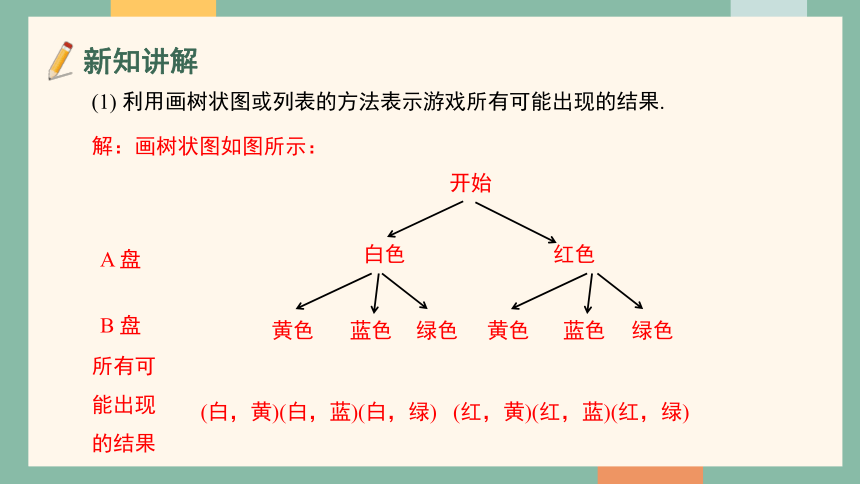
(1) 利用画树状图或列表的方法表示游戏所有可能出现的结果.
解:画树状图如图所示:
开始
白色
红色
黄色
绿色
A 盘
B 盘
蓝色
黄色
绿色
蓝色
所有可能出现的结果
(白,黄)(白,蓝)(白,绿) (红,黄)(红,蓝)(红,绿)
B 盘 A 盘 黄色 蓝色 绿色
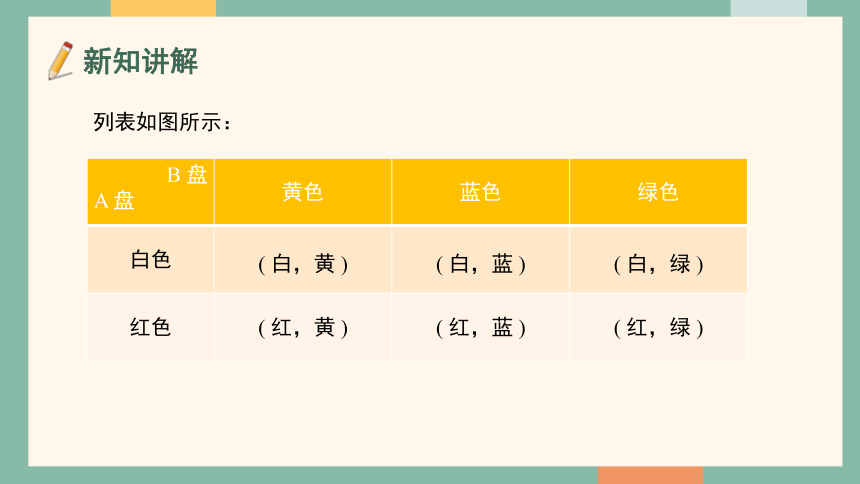
白色 ( 白,黄 ) ( 白,蓝 ) ( 白,绿 )
红色 ( 红,黄 ) ( 红,蓝 ) ( 红,绿 )
列表如图所示:
(2) 游戏者获胜的概率是多少?
(2) 由 (1) 可知,所有等可能的结果为 6 种,其中配成紫色 ( 红,蓝 ) 的可能性只有 1 种,则游戏获胜的概率为 .
思考
用画树状图和列表的方法求概率时应注意些什么?
用树状图和列表的方法求概率时应注意各种结果出现的可能性务必相同.
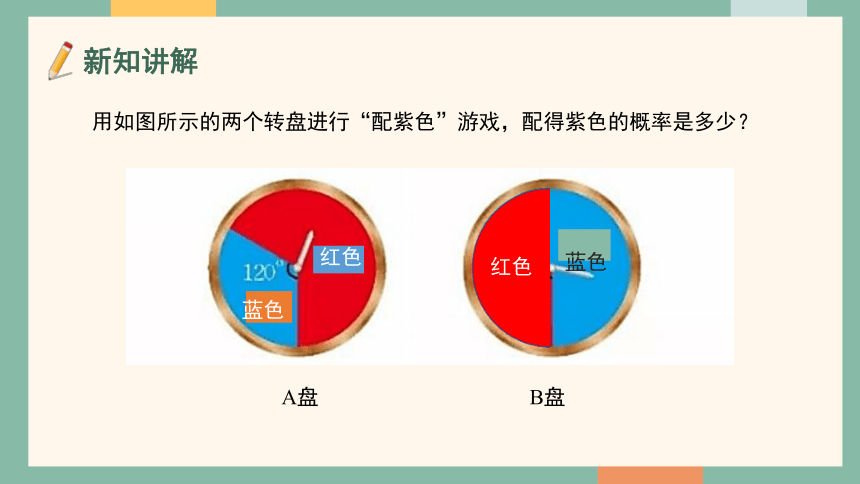
用如图所示的两个转盘进行“配紫色”游戏,配得紫色的概率是多少?
蓝色
红色
蓝色
红色
B盘
A盘
小颖制作了下图,并据此求出获胜者获胜的概率为
开始
红
蓝
红
( 红,红 )
蓝
( 红,蓝 )
红
( 蓝,红 )
蓝
( 蓝,蓝 )
蓝色
蓝色
红色
红色
B盘
A盘
小亮则先把转盘 A 的红色区域等分成 2 份,分别记作“红色1”“红色 2”,然后制作了下表,据此求出游戏者获胜的概率也是
蓝色
蓝色
红色
红色
B盘
A盘
蓝色
蓝色
红色
红色
B盘
A盘
B盘 A盘 红色 蓝色
红色1 (红1,红) (红1,蓝)
红色2 (红2,红) (红2,蓝)
蓝色 (蓝,红) (蓝,蓝)
你认为谁的对?为什么?
利用等可能事件的概率公式计算事件的概率,需建立在所有的结果都是等可能的基础上,然后利用列表法或画树状图法求解.
温馨提示
1. 用如图所示的两个转盘进行“配紫色”游戏,每个转盘都被分成面积相等的三个扇形,配得紫色的概率是多少?
红
蓝
白
A盘
红
蓝
黄
B盘
开始
红
白
蓝
红
黄
蓝
A盘
B盘
所有可能出现的结果
( 红,红 )
( 红,黄 )
( 红,蓝 )
( 白,红 )
( 白,黄 )
( 白,蓝 )
( 蓝,红 )
( 蓝,黄 )
( 蓝,蓝 )
红
黄
蓝
红
黄
蓝
解:利用树状图列出所有可能出现的结果如下:
2. 用如图所示的两个转盘进行“配紫色”游戏,配得紫色的概率是多少?
蓝色
红色
蓝色
B盘
A盘
红色
由图可知,所有等可能的结果为 9 种,
其中配成紫色 ( 红,蓝 ) 的可能性只有 2 种,则配成紫色的概率为 .
请你用列表法算一算配成紫色的概率!
思考
本题如何将两个转盘转换为等可能结果?
转动 A 盘( A 盘两部分面积不相等 ) → 转化为 3 个面积相等的扇形部分→3 种等可能的结果 ( 圆心角均为 120° )
转动B盘 ( B 盘两部分面积不相等 ) → 转化为 3 个面积相等的扇形部分→3 种等可能的结果 ( 圆心角均为 120° )
解:利用列表法列出所有可能出现的结果如下:
B盘 A盘 蓝色 1 蓝色 2 红色
红色 1 ( 红色 1,蓝色 1 ) ( 红色 1,蓝色 2 ) ( 红色 1,红色 )
红色 2 ( 红色 2,蓝色 1 ) ( 红色 2,蓝色 2 ) ( 红色 2,红色 )
蓝色 ( 蓝色,蓝色 1 ) ( 蓝色,蓝色 2 ) ( 蓝色,红色 )
由上表可知,所有等可能的结果为 9 种,
其中配成紫色的所有可能性有 5 种,则配成紫色的概率为 .
由“配紫色”游戏得到了什么
用树状图和列表的方法求概率时应注意各种结果出现的可能性务必相同.
“配紫色”游戏体现了概率模型的思想,它启示我们:概率是对随机现象的一种数学描述,它可以帮助我们更好地认识随机现象,并对生活中的一些不确定情况做出自己的决策.
3.1 课时3 用树状图或
表格分析配紫色游戏的概率
1.通过配色游戏,进一步体会用树状图、表格法计算概率;
2.用树状图和表格法计算随机事件发生的概率.
3.在利用树状图或者列表法求概率时,各种情况出现可能性不同时的情况处理.
B盘
A盘
红
蓝
白
黄
绿
B盘
小颖为学校联欢会设计了一个“配紫色”游戏:下面是两个可以自由转动的转盘,每个转盘被分成面积相等的几个扇形. 游戏者同时转动两个转盘,如果转盘 A 转出了红色,转盘 B 转出了蓝色,那么他就赢了,因为红色和蓝色在一起配成了紫色.
(1) 利用画树状图或列表的方法表示游戏所有可能出现的结果.
解:画树状图如图所示:
开始
白色
红色
黄色
绿色
A 盘
B 盘
蓝色
黄色
绿色
蓝色
所有可能出现的结果
(白,黄)(白,蓝)(白,绿) (红,黄)(红,蓝)(红,绿)
B 盘 A 盘 黄色 蓝色 绿色
白色 ( 白,黄 ) ( 白,蓝 ) ( 白,绿 )
红色 ( 红,黄 ) ( 红,蓝 ) ( 红,绿 )
列表如图所示:
(2) 游戏者获胜的概率是多少?
(2) 由 (1) 可知,所有等可能的结果为 6 种,其中配成紫色 ( 红,蓝 ) 的可能性只有 1 种,则游戏获胜的概率为 .
思考
用画树状图和列表的方法求概率时应注意些什么?
用树状图和列表的方法求概率时应注意各种结果出现的可能性务必相同.
用如图所示的两个转盘进行“配紫色”游戏,配得紫色的概率是多少?
蓝色
红色
蓝色
红色
B盘
A盘
小颖制作了下图,并据此求出获胜者获胜的概率为
开始
红
蓝
红
( 红,红 )
蓝
( 红,蓝 )
红
( 蓝,红 )
蓝
( 蓝,蓝 )
蓝色
蓝色
红色
红色
B盘
A盘
小亮则先把转盘 A 的红色区域等分成 2 份,分别记作“红色1”“红色 2”,然后制作了下表,据此求出游戏者获胜的概率也是
蓝色
蓝色
红色
红色
B盘
A盘
蓝色
蓝色
红色
红色
B盘
A盘
B盘 A盘 红色 蓝色
红色1 (红1,红) (红1,蓝)
红色2 (红2,红) (红2,蓝)
蓝色 (蓝,红) (蓝,蓝)
你认为谁的对?为什么?
利用等可能事件的概率公式计算事件的概率,需建立在所有的结果都是等可能的基础上,然后利用列表法或画树状图法求解.
温馨提示
1. 用如图所示的两个转盘进行“配紫色”游戏,每个转盘都被分成面积相等的三个扇形,配得紫色的概率是多少?
红
蓝
白
A盘
红
蓝
黄
B盘
开始
红
白
蓝
红
黄
蓝
A盘
B盘
所有可能出现的结果
( 红,红 )
( 红,黄 )
( 红,蓝 )
( 白,红 )
( 白,黄 )
( 白,蓝 )
( 蓝,红 )
( 蓝,黄 )
( 蓝,蓝 )
红
黄
蓝
红
黄
蓝
解:利用树状图列出所有可能出现的结果如下:
2. 用如图所示的两个转盘进行“配紫色”游戏,配得紫色的概率是多少?
蓝色
红色
蓝色
B盘
A盘
红色
由图可知,所有等可能的结果为 9 种,
其中配成紫色 ( 红,蓝 ) 的可能性只有 2 种,则配成紫色的概率为 .
请你用列表法算一算配成紫色的概率!
思考
本题如何将两个转盘转换为等可能结果?
转动 A 盘( A 盘两部分面积不相等 ) → 转化为 3 个面积相等的扇形部分→3 种等可能的结果 ( 圆心角均为 120° )
转动B盘 ( B 盘两部分面积不相等 ) → 转化为 3 个面积相等的扇形部分→3 种等可能的结果 ( 圆心角均为 120° )
解:利用列表法列出所有可能出现的结果如下:
B盘 A盘 蓝色 1 蓝色 2 红色
红色 1 ( 红色 1,蓝色 1 ) ( 红色 1,蓝色 2 ) ( 红色 1,红色 )
红色 2 ( 红色 2,蓝色 1 ) ( 红色 2,蓝色 2 ) ( 红色 2,红色 )
蓝色 ( 蓝色,蓝色 1 ) ( 蓝色,蓝色 2 ) ( 蓝色,红色 )
由上表可知,所有等可能的结果为 9 种,
其中配成紫色的所有可能性有 5 种,则配成紫色的概率为 .
由“配紫色”游戏得到了什么
用树状图和列表的方法求概率时应注意各种结果出现的可能性务必相同.
“配紫色”游戏体现了概率模型的思想,它启示我们:概率是对随机现象的一种数学描述,它可以帮助我们更好地认识随机现象,并对生活中的一些不确定情况做出自己的决策.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
