人教版三年级上册数学 周长的认识 表格式教学设计
文档属性
| 名称 | 人教版三年级上册数学 周长的认识 表格式教学设计 |  | |
| 格式 | docx | ||
| 文件大小 | 443.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-07 21:36:09 | ||
图片预览


文档简介
教学设计
课程基本信息
学科 小学数学 年级 三年级 学期 秋季
课题 周长的认识
教学目标
1.通过亲身体验,区分平面图形的“面”和“周”,体会这两个概念的联系与区别。 2.经历从图形取“周”的三种方法(用手比划、用直尺测量、尺规取周),不断优化取周的策 略,掌握用直尺和圆规将三角形的三条边画到一条直线上的方法,感受数学的严谨性。 3.在剥离“周”的过程中,认识到“周”具有首尾相接的特点,通过直尺测量展开的线段的 长度,感知线段长度的可加性。 4.理解并内化“周长”的概念,明晰周长的本质就是长度单位的累加,掌握测量图形周长的通法。在探索的过程中,形成初步的几何直观和量感。 5.结合具体情境体会周长与实际生活的联系,感受数学学习的应用价值。
教学内容
教学重点: 认识理解周长的意义,会测量图形的周长。
教学难点: 建立“周”和“长”的空间观念。
教学过程
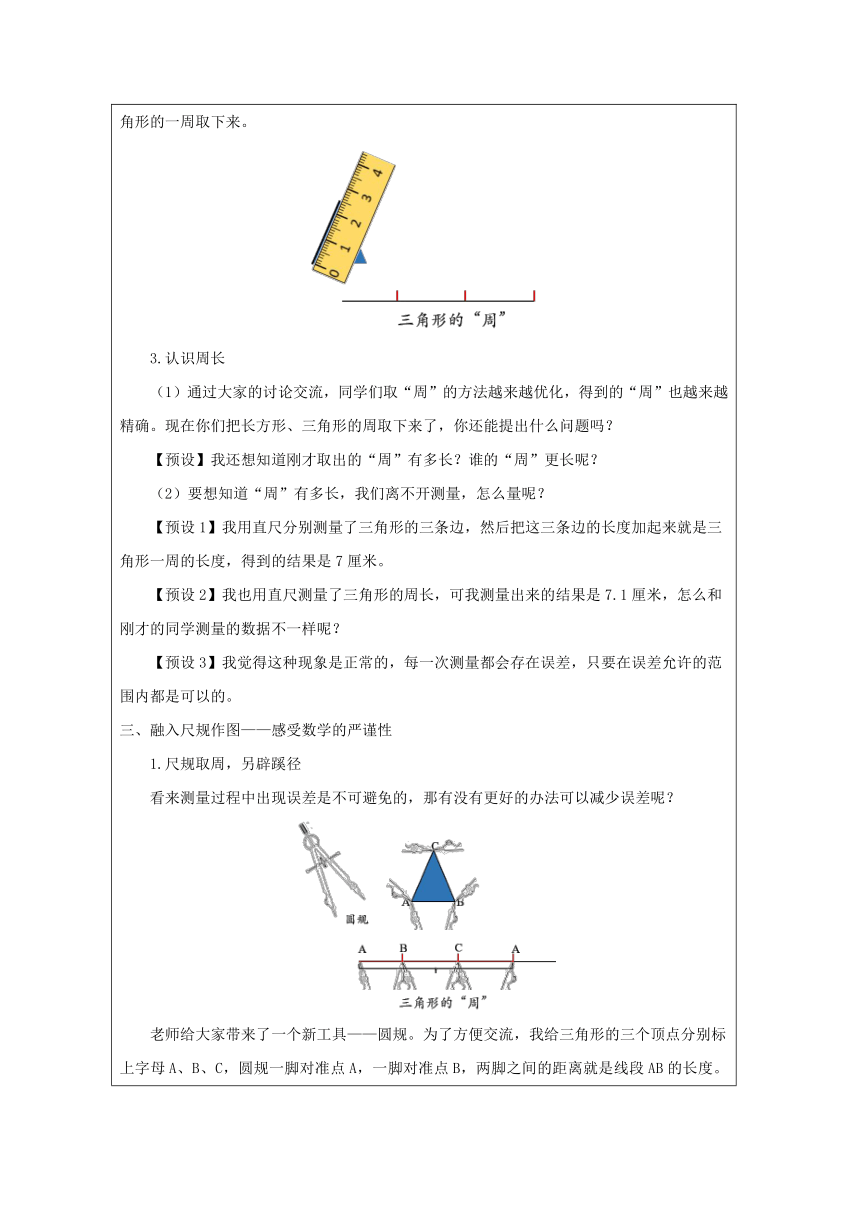
一、凸显研究对象——“周”是一条线,“面”是一大片 1.回顾面,感受边 今天老师带来了三张卡片,你一眼看到了什么? 【预设1】我看到了三张卡片的颜色有橙色、蓝色和绿色。 【预设2】我看到了它们形状不同,有长方形、三角形还有正方形,它们上面都有平平的面。 【预设3】我还看见了长方形有四条边。 小结:一个图形一圈的边线叫做一周。 2.感知“面”与“周”的联系与区别 刚才你们找到了图形的面与周,周和面是一回事儿吗? 【预设1】面在周的里边,周在面的外边。面是平平的一大片,周是细细的一圈。 【预设2】周和面确实是不同的,但它们之间也是有关系的,没有面就没有周,没有周 也没有面,周和面不能分家,它们谁也离不开谁,是连着的一对好朋友。 小结:周和面是不一样的,面是平平的,周是细细的。可是‘面’长在‘周’的里面, ‘周’长在‘面’的外面,它们之间形影不离。 二、明晰周长本质——周是周,长是长,周长是周长 1.剥长方形的“周” 从选定的起点A开始,把事先粘贴好的边线往下剥,最后又回到了A点,正好是一周。长方形的一周是由4条边围成的,把这些线段首尾相接依次排列就是长方形的一周。 2.剥三角形的“周” 三角形在没有线围一圈的情况下,你们有什么办法把这一段一段的线段取下来? 【预设1】我用手比划把三角形的三条边分别取下来,首尾顺次相接就得到了三角形的 一周。 【预设2】我发现用手比划的时候,两只手会不由自主动了一下,结果不是太准确,所 以我想到用尺子去量每一条边的长度,再一段一段把它们取下来,重复操作三次也可以把三角形的一周取下来。 3.认识周长 (1)通过大家的讨论交流,同学们取“周”的方法越来越优化,得到的“周”也越来越 精确。现在你们把长方形、三角形的周取下来了,你还能提出什么问题吗? 【预设】我还想知道刚才取出的“周”有多长?谁的“周”更长呢? (2)要想知道“周”有多长,我们离不开测量,怎么量呢? 【预设1】我用直尺分别测量了三角形的三条边,然后把这三条边的长度加起来就是三 角形一周的长度,得到的结果是7厘米。 【预设2】我也用直尺测量了三角形的周长,可我测量出来的结果是7.1厘米,怎么和 刚才的同学测量的数据不一样呢? 【预设3】我觉得这种现象是正常的,每一次测量都会存在误差,只要在误差允许的范 围内都是可以的。 三、融入尺规作图——感受数学的严谨性 1.尺规取周,另辟蹊径 看来测量过程中出现误差是不可避免的,那有没有更好的办法可以减少误差呢? 老师给大家带来了一个新工具——圆规。为了方便交流,我给三角形的三个顶点分别标 上字母A、B、C,圆规一脚对准点A,一脚对准点B,两脚之间的距离就是线段AB的长度。接下来我们再用直尺画一条长长的线段,用圆规在线段上分别截取线段AB、线段BC和线段AC,这三条线段首尾相接,没有空隙,就是三角形的周。 2.对比方法,优化策略 尺规取“周”的方法对你们有什么启发吗? 【预设1】我觉得用尺规取“周”又快速又准确。 【预设2】我发现这种方法只需要用直尺测量一次就可以得到三角形的周长,是7厘米。 小结:尺规作图不仅减少了测量的次数,还增加了测量的准确性,真是一种好方法! 3.尺规量“周”,掌握方法 你们能用刚才的方法测量正方形的周长吗? 【预设1】可以用圆规帮忙把正方形的四条边都取下来连成一条线段,再量一量,这时 量出来的长度就是正方形的周长。 【预设2】正方形的四条边是一样长的,所以我觉得只要测量出正方形一条边的长,乘4 也可以得到正方形的周长。 小结:看来我们不仅可以用尺规作图的方法得到正方形的周长,还可以根据正方形的特 征灵活选择简洁的方法进行计算。 4.深挖本质,融会贯通 解决了“周”的测量问题,再看这些“周”,你们还有什么想说的吗? 【预设1】我发现图形的“周”最终的模样就是一段一段的线段首尾相接形成的直线段, 测量之前需要借助尺规将这些“周”取下来再用有刻度的直尺进行测量,测量图形的周长其实就是在测量线段的长度。 【预设2】我觉得测量周长和测量线段的长度一样,都离不开测量单位,我们这节课总 是用到直尺,直尺上的刻度不就是给我们提供了测量单位嘛,有了单位,再数一数一周中所包含的单位的个数,就能知道图形的周长了。 【预设3】在操作过程中,我还发现了圆规的一个功能,在不需要具体测量结果的情况 下,圆规可以帮助我们比较不同图形的周长,圆规两脚张开的距离越大,图形的一周越长。 四、巩固拓展,应用概念 1.下图是一个公园的示意图。王奶奶绕着公园走一圈大约是多少米? 【预设】王奶奶绕公园走一圈的距离其实就是这个不规则图形的周长,已知图形中每一 条边的长度,把这些长度加起来就是公园的周长。20+80+180+100+150=530(米) 小结:看来只要理解了周长的意义,掌握了计算周长的通法,就可以解决图形周长的相关问题了。 2.正六边形的周长,你们会算吗? 【预设1】根据计算周长的方法,我们可以先用尺规将正六边形的“周”取下来,然后 再用有刻度的直尺去测量,得到的结果就是正六边形的周长。 【预设2】我发现正六边形每条边的长度都是相等的,所以只需要测量一条边的长度,再乘6也能计算正六边形的周长。 3.借助这样的经验,你能解决正八边形、正十六边形、正三十二边形等正多边形的周长计算问题吗? 【预设】我发现不管是正几边形,由于每一条边的长度都是相等的,所以都可以用每条 边的长度乘边数的方法计算正多边形的周长。 小结:同学们真善于归纳总结。我们既可以用尺规这种通法计算图形的周长,也可以用 简便方法计算一些特殊图形的周长,要根据解决的问题灵活选择。随着正多边形的边数越来越多,大家想象一下,你们有什么新的发现吗? 【预设】我发现随着正多边形的边数越来越多,图形好像变成了一个圆,圆是不是也是 正多边形呢?圆的周长计算问题是不是也可以借助正多边形的周长计算经验呢。
课程基本信息
学科 小学数学 年级 三年级 学期 秋季
课题 周长的认识
教学目标
1.通过亲身体验,区分平面图形的“面”和“周”,体会这两个概念的联系与区别。 2.经历从图形取“周”的三种方法(用手比划、用直尺测量、尺规取周),不断优化取周的策 略,掌握用直尺和圆规将三角形的三条边画到一条直线上的方法,感受数学的严谨性。 3.在剥离“周”的过程中,认识到“周”具有首尾相接的特点,通过直尺测量展开的线段的 长度,感知线段长度的可加性。 4.理解并内化“周长”的概念,明晰周长的本质就是长度单位的累加,掌握测量图形周长的通法。在探索的过程中,形成初步的几何直观和量感。 5.结合具体情境体会周长与实际生活的联系,感受数学学习的应用价值。
教学内容
教学重点: 认识理解周长的意义,会测量图形的周长。
教学难点: 建立“周”和“长”的空间观念。
教学过程
一、凸显研究对象——“周”是一条线,“面”是一大片 1.回顾面,感受边 今天老师带来了三张卡片,你一眼看到了什么? 【预设1】我看到了三张卡片的颜色有橙色、蓝色和绿色。 【预设2】我看到了它们形状不同,有长方形、三角形还有正方形,它们上面都有平平的面。 【预设3】我还看见了长方形有四条边。 小结:一个图形一圈的边线叫做一周。 2.感知“面”与“周”的联系与区别 刚才你们找到了图形的面与周,周和面是一回事儿吗? 【预设1】面在周的里边,周在面的外边。面是平平的一大片,周是细细的一圈。 【预设2】周和面确实是不同的,但它们之间也是有关系的,没有面就没有周,没有周 也没有面,周和面不能分家,它们谁也离不开谁,是连着的一对好朋友。 小结:周和面是不一样的,面是平平的,周是细细的。可是‘面’长在‘周’的里面, ‘周’长在‘面’的外面,它们之间形影不离。 二、明晰周长本质——周是周,长是长,周长是周长 1.剥长方形的“周” 从选定的起点A开始,把事先粘贴好的边线往下剥,最后又回到了A点,正好是一周。长方形的一周是由4条边围成的,把这些线段首尾相接依次排列就是长方形的一周。 2.剥三角形的“周” 三角形在没有线围一圈的情况下,你们有什么办法把这一段一段的线段取下来? 【预设1】我用手比划把三角形的三条边分别取下来,首尾顺次相接就得到了三角形的 一周。 【预设2】我发现用手比划的时候,两只手会不由自主动了一下,结果不是太准确,所 以我想到用尺子去量每一条边的长度,再一段一段把它们取下来,重复操作三次也可以把三角形的一周取下来。 3.认识周长 (1)通过大家的讨论交流,同学们取“周”的方法越来越优化,得到的“周”也越来越 精确。现在你们把长方形、三角形的周取下来了,你还能提出什么问题吗? 【预设】我还想知道刚才取出的“周”有多长?谁的“周”更长呢? (2)要想知道“周”有多长,我们离不开测量,怎么量呢? 【预设1】我用直尺分别测量了三角形的三条边,然后把这三条边的长度加起来就是三 角形一周的长度,得到的结果是7厘米。 【预设2】我也用直尺测量了三角形的周长,可我测量出来的结果是7.1厘米,怎么和 刚才的同学测量的数据不一样呢? 【预设3】我觉得这种现象是正常的,每一次测量都会存在误差,只要在误差允许的范 围内都是可以的。 三、融入尺规作图——感受数学的严谨性 1.尺规取周,另辟蹊径 看来测量过程中出现误差是不可避免的,那有没有更好的办法可以减少误差呢? 老师给大家带来了一个新工具——圆规。为了方便交流,我给三角形的三个顶点分别标 上字母A、B、C,圆规一脚对准点A,一脚对准点B,两脚之间的距离就是线段AB的长度。接下来我们再用直尺画一条长长的线段,用圆规在线段上分别截取线段AB、线段BC和线段AC,这三条线段首尾相接,没有空隙,就是三角形的周。 2.对比方法,优化策略 尺规取“周”的方法对你们有什么启发吗? 【预设1】我觉得用尺规取“周”又快速又准确。 【预设2】我发现这种方法只需要用直尺测量一次就可以得到三角形的周长,是7厘米。 小结:尺规作图不仅减少了测量的次数,还增加了测量的准确性,真是一种好方法! 3.尺规量“周”,掌握方法 你们能用刚才的方法测量正方形的周长吗? 【预设1】可以用圆规帮忙把正方形的四条边都取下来连成一条线段,再量一量,这时 量出来的长度就是正方形的周长。 【预设2】正方形的四条边是一样长的,所以我觉得只要测量出正方形一条边的长,乘4 也可以得到正方形的周长。 小结:看来我们不仅可以用尺规作图的方法得到正方形的周长,还可以根据正方形的特 征灵活选择简洁的方法进行计算。 4.深挖本质,融会贯通 解决了“周”的测量问题,再看这些“周”,你们还有什么想说的吗? 【预设1】我发现图形的“周”最终的模样就是一段一段的线段首尾相接形成的直线段, 测量之前需要借助尺规将这些“周”取下来再用有刻度的直尺进行测量,测量图形的周长其实就是在测量线段的长度。 【预设2】我觉得测量周长和测量线段的长度一样,都离不开测量单位,我们这节课总 是用到直尺,直尺上的刻度不就是给我们提供了测量单位嘛,有了单位,再数一数一周中所包含的单位的个数,就能知道图形的周长了。 【预设3】在操作过程中,我还发现了圆规的一个功能,在不需要具体测量结果的情况 下,圆规可以帮助我们比较不同图形的周长,圆规两脚张开的距离越大,图形的一周越长。 四、巩固拓展,应用概念 1.下图是一个公园的示意图。王奶奶绕着公园走一圈大约是多少米? 【预设】王奶奶绕公园走一圈的距离其实就是这个不规则图形的周长,已知图形中每一 条边的长度,把这些长度加起来就是公园的周长。20+80+180+100+150=530(米) 小结:看来只要理解了周长的意义,掌握了计算周长的通法,就可以解决图形周长的相关问题了。 2.正六边形的周长,你们会算吗? 【预设1】根据计算周长的方法,我们可以先用尺规将正六边形的“周”取下来,然后 再用有刻度的直尺去测量,得到的结果就是正六边形的周长。 【预设2】我发现正六边形每条边的长度都是相等的,所以只需要测量一条边的长度,再乘6也能计算正六边形的周长。 3.借助这样的经验,你能解决正八边形、正十六边形、正三十二边形等正多边形的周长计算问题吗? 【预设】我发现不管是正几边形,由于每一条边的长度都是相等的,所以都可以用每条 边的长度乘边数的方法计算正多边形的周长。 小结:同学们真善于归纳总结。我们既可以用尺规这种通法计算图形的周长,也可以用 简便方法计算一些特殊图形的周长,要根据解决的问题灵活选择。随着正多边形的边数越来越多,大家想象一下,你们有什么新的发现吗? 【预设】我发现随着正多边形的边数越来越多,图形好像变成了一个圆,圆是不是也是 正多边形呢?圆的周长计算问题是不是也可以借助正多边形的周长计算经验呢。
