2.2 课时1 位移变化规律 课件 (共25张PPT)2024-2025学年高一物理鲁科版(2019)必修第一册第2章 匀变速直线运动
文档属性
| 名称 | 2.2 课时1 位移变化规律 课件 (共25张PPT)2024-2025学年高一物理鲁科版(2019)必修第一册第2章 匀变速直线运动 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-08-08 00:00:00 | ||
图片预览





文档简介
(共25张PPT)
第二章 匀变速直线运动
第2节 课时1 位移变化规律
公式法
1. 位移公式 s=vt
2. 速度时间图象(v-t图象)
图象法
平行于时间轴的直线
结论:匀速直线运动的v – t 图象与t轴所围的矩形“面积”就等于“位移”。
v
(m·s-1)
/
t
s
/
v0
o
t
匀变速直线运动的位移是否也可以用v-t图象与t轴所围的“面积”表示呢?
1.能运用微积分的思想根据速度-时间图像推证位移-时间关系式。
2.了解位移-时间图像的物理意义,会运用图像研究匀变速直线运动。
3.会推导位移-速度的关系式,并会用位移-速度公式进行计算。
01 匀变速直线运动的位移
1
理论探究 匀变速直线运动 v-t 图象及其含义
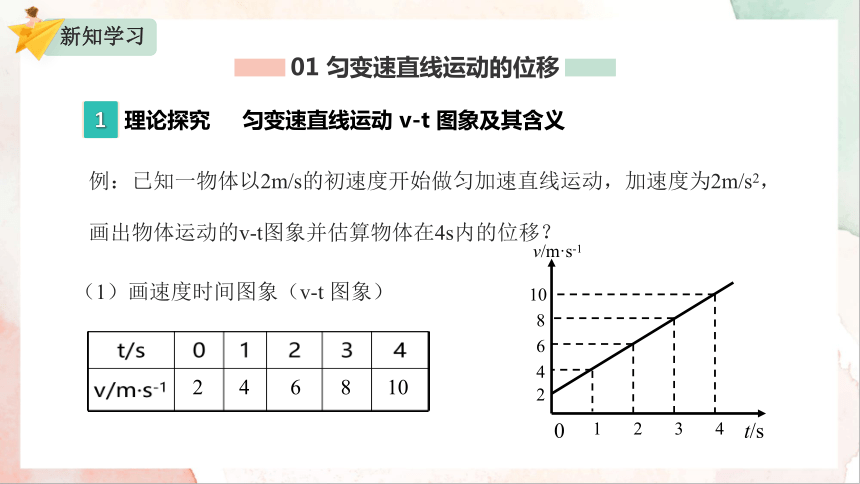
例:已知一物体以2m/s的初速度开始做匀加速直线运动,加速度为2m/s2,画出物体运动的v-t图象并估算物体在4s内的位移?
t/s
4
3
2
1
0
2
4
6
10
8
v/m·s-1
(1)画速度时间图象(v-t 图象)
2
4
6
8
10
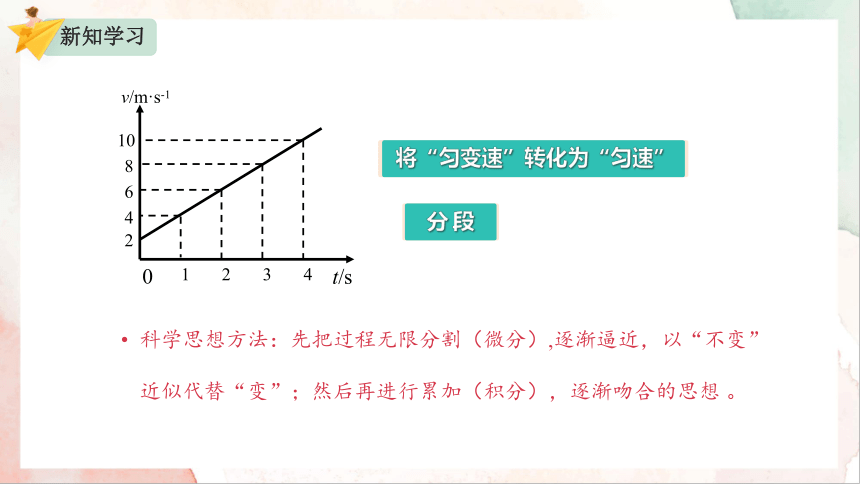
将“匀变速”转化为“匀速”
分 段
科学思想方法:先把过程无限分割(微分),逐渐逼近,以“不变”近似代替“变”;然后再进行累加(积分),逐渐吻合的思想 。
t/s
4
3
2
1
0
2
4
6
10
8
v/m·s-1
t/s
4
3
2
1
0
2
4
6
10
8
v/m·s-1
t/s
4
3
2
1
0
2
4
6
10
8
v/m·s-1
t/s
4
3
2
1
0
2
4
6
10
8
v/m·s-1
t/s
4
3
2
1
0
2
4
6
10
8
v/m·s-1
t/s
4
3
2
1
0
2
4
6
10
8
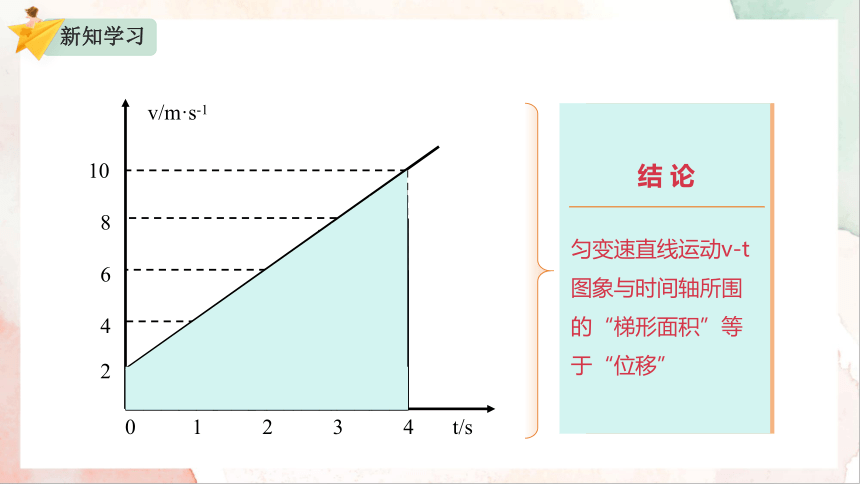
结 论
匀变速直线运动v-t 图象与时间轴所围的“梯形面积”等于“位移”
v/m·s-1
2
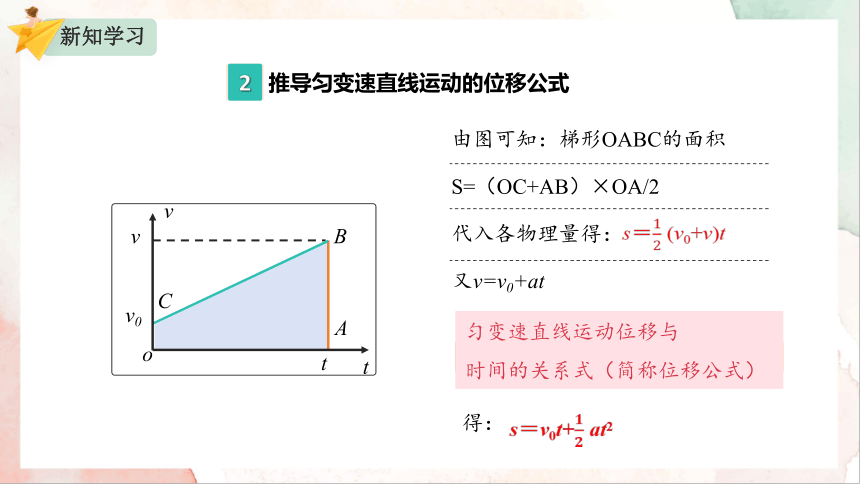
推导匀变速直线运动的位移公式
由图可知:梯形OABC的面积
S=(OC+AB)×OA/2
代入各物理量得:
又v=v0+at
v
v0
v
B
A
o
t
t
C
得:
匀变速直线运动位移与
时间的关系式(简称位移公式)
s=v0t+ at2
s= (v0+v)t
v/(m·s-1)
O
t
t/s
v0
vt
总位移=
匀速过程的位移
静止开始匀加速位移
s
(5)公式中4个物理量(不涉及末速度),知任三求剩一;代入数据时,各物理量的单位要统一 (一般用国际制单位) 。
(1)反映了匀变速直线运动的位移与时间是二次函数关系,x-t图象是一元二次函数曲线(抛物线)。
(2)公式适用于匀变速(包括匀加速或匀减速)直线运动。
(3)是矢量式,使用公式时应先规定正方向。(一般取v0的方向为正方向)若物体做匀加速运动,a取正值;若物体做匀减速运动,则a取负值。
(4) 若位移的计算结果为正值,说明位移方向与规定的正方向相同;若位移的计算结果为负值,说明位移方向与规定的正方向相反。
3
对位移公式的理解
① 当v0=0时,s= ,即由静止开始的匀加速直线运动,位移s与t2成正比。
② 当a=0时,s=v0t,即匀速直线运动的位移公式。
注 意
逆向思维法:末速度为 0 的匀减速直线运动可视为反方向的初速度为 0 的匀加速直线运动。
4
位移与时间关系的两种特殊形式
t/s 0 1 2 3 4 5 6
s(m)
因为小车初速度为0,加速度为2m/s2,根据x=at2可求出汽车的位移。
以第二章第1节图2-1所示的汽车运动为例。
0
2
4
9
16
25
36
选汽车行驶的时间t为横坐标,汽车相对起点位置的位移s为纵坐标,分别在坐标纸上描出相应的点,再将各点用平滑曲线连接起来。
t/s
s/m
o
1
2
3
4
5
6
5
10
15
20
25
5
匀变速直线运动的s-t图像
t/s
s/m
o
1
2
3
4
5
6
5
10
15
20
25
从s-t图像中我们可直观看出物体运动过程中位移随时间的变化情况,并可求出不同时间内物体运动的位移。
注意:s-t图象不是物体运动的轨迹,而是位移随时间变化的规律。
a不变
位移
v=v0+at
?
时间
位移
速度
速度时间关系
位移时间关系
速度位移关系
s
如图所示,狙击步枪射击时,若把子弹在枪筒中的运动看作是匀加速直线运动,假设枪筒长s,子弹的加速度为a.
(1)如何求出子弹射出枪口的速度大小?
(2)在上面问题中,已知条件和所求的结果都不涉及时间t,它只是一个中间量,能否将两个公式联立,消去t,只用一个关系式表示位移s与速度vt的关系呢?
02 匀变速直线运动的位移-速度关系
(2)位移与时间的关系式:s=v0t+ at2
速度与时间的关系式:vt= v0 +at
将上述两个公式联立求解,消去时间 t 可得到
v2-v02=2as
(1)由s=at2,vt=at得vt=
公式意义
适用范围
优点
矢量性
两种特 殊形式
速度与位移的关系
匀变速直线运动
该式不涉及时间,研究的问题中若不涉及时间,利用该式求解更加方便
其中的s、v、v0、a都是矢量,应用时必须选取统一的正方向。
若选初速度v0的方向为正方向:
(1)物体做匀加速直线运动,a取正值;
(2)物体做匀减速直线运动,a取负值
(1)当v0=0时,v2=2as→初速度为零的匀加速直线运动;
(2)当v=0时,-v02=2as→末速度为零的匀减速直线运动。
例题:汽车从开始制动到停止所行驶的距离,是衡量汽车制动性能的参数之一。某型号的汽车以100 km/h的速度在柏油路面上行驶,急刹车后做匀减速直线运动。若匀减速时的加速度大小为5m/s2,开始制动后2s内汽车行驶的距离是多少?从开始制动到完全停止,汽车行驶的距离是多少?
[分析]汽车刹车后做匀减速直线运动,运动过程如图所示。在第一问中,已知初速度、加速度和时间的信息求位移,可用位移-时间关系式;在第二问中,通过初速度、加速度和末速度的信息求位移,可用位移-速度关系式。
解:选定初速度方向为正方向,由题意知v0=100 km/h=27.8 m/s,a=-5 m/s2,vt=0,t=2 s
根据速度公式vt=v0+at,可知汽车刹车时间
因为t“刹车类”问题的处理方法
(1)刹车类问题一般视为匀减速直线运动,汽车停下后不能做反向的运动。
(2)处理该类问题时,首先要判断刹车后经多长时间速度变为零(即刹车时间)。
①若所给时间大于刹车时间,则v=0,s=v0t0+,t0为刹车时间或s=-。
②若所给时间小于刹车时间,则v=v0+at,s=v0t+at2,t为所给时间。
1.100m决赛中,某运动员的起跑反应时间是0.170s,加速过程可以看成匀加速直线运动,加速时间约为2.5s,最大速度约为12m/s,则该运动员在加速阶段的加速度与位移约为( )
A.4.8m/s2 16m B.4.8m/s2 15m
C.4.5m/s2 16m D.4.5m/s2 15m
B
2.一物体以2 m/s的初速度做匀加速直线运动,4 s内的位移为16 m,则 ( )
A.物体的加速度大小为2 m/s2
B.物体在4 s内的平均速度大小为6 m/s
C.物体在4 s末的瞬时速度大小为6 m/s
D.物体在第2 s内的位移大小为6 m
C
3.如图所示,70周年国庆国旗时,国歌从响起到结束的时间是48s,国旗上升的高度是17.6m。国歌响起同时国旗开始向上做匀加速运动4s,然后匀速运动,最后匀减速运动4s到达旗杆顶端,速度恰好为零,此时国歌结束。求:
(1)国旗匀加速运动的加速度大小。
(2)国旗匀速运动时的速度大小。
解:由题意知,国旗匀加速上升时间t1=4s,匀减速上升时间t3=4s,匀速上升时间t2=t总-t1-t3=40s,
对于国旗加速上升阶段:s1=
对于国旗匀速上升阶段v=a1t1,s2=vt2
对于国旗减速上升阶段:s3=vt3-
根据运动对称性,对于全过程:a1=a2
s1+s2+s3=17.6m
由以上各式可得a1=0.1m/s2;v=0.4m/s。
位移的变化规律
v-t图象所围面积的意义
位移-时间公式x=v0t+ at2的推导和应用
速度-位移公式v2–v02 =2ax的推导和应用
第二章 匀变速直线运动
第2节 课时1 位移变化规律
公式法
1. 位移公式 s=vt
2. 速度时间图象(v-t图象)
图象法
平行于时间轴的直线
结论:匀速直线运动的v – t 图象与t轴所围的矩形“面积”就等于“位移”。
v
(m·s-1)
/
t
s
/
v0
o
t
匀变速直线运动的位移是否也可以用v-t图象与t轴所围的“面积”表示呢?
1.能运用微积分的思想根据速度-时间图像推证位移-时间关系式。
2.了解位移-时间图像的物理意义,会运用图像研究匀变速直线运动。
3.会推导位移-速度的关系式,并会用位移-速度公式进行计算。
01 匀变速直线运动的位移
1
理论探究 匀变速直线运动 v-t 图象及其含义
例:已知一物体以2m/s的初速度开始做匀加速直线运动,加速度为2m/s2,画出物体运动的v-t图象并估算物体在4s内的位移?
t/s
4
3
2
1
0
2
4
6
10
8
v/m·s-1
(1)画速度时间图象(v-t 图象)
2
4
6
8
10
将“匀变速”转化为“匀速”
分 段
科学思想方法:先把过程无限分割(微分),逐渐逼近,以“不变”近似代替“变”;然后再进行累加(积分),逐渐吻合的思想 。
t/s
4
3
2
1
0
2
4
6
10
8
v/m·s-1
t/s
4
3
2
1
0
2
4
6
10
8
v/m·s-1
t/s
4
3
2
1
0
2
4
6
10
8
v/m·s-1
t/s
4
3
2
1
0
2
4
6
10
8
v/m·s-1
t/s
4
3
2
1
0
2
4
6
10
8
v/m·s-1
t/s
4
3
2
1
0
2
4
6
10
8
结 论
匀变速直线运动v-t 图象与时间轴所围的“梯形面积”等于“位移”
v/m·s-1
2
推导匀变速直线运动的位移公式
由图可知:梯形OABC的面积
S=(OC+AB)×OA/2
代入各物理量得:
又v=v0+at
v
v0
v
B
A
o
t
t
C
得:
匀变速直线运动位移与
时间的关系式(简称位移公式)
s=v0t+ at2
s= (v0+v)t
v/(m·s-1)
O
t
t/s
v0
vt
总位移=
匀速过程的位移
静止开始匀加速位移
s
(5)公式中4个物理量(不涉及末速度),知任三求剩一;代入数据时,各物理量的单位要统一 (一般用国际制单位) 。
(1)反映了匀变速直线运动的位移与时间是二次函数关系,x-t图象是一元二次函数曲线(抛物线)。
(2)公式适用于匀变速(包括匀加速或匀减速)直线运动。
(3)是矢量式,使用公式时应先规定正方向。(一般取v0的方向为正方向)若物体做匀加速运动,a取正值;若物体做匀减速运动,则a取负值。
(4) 若位移的计算结果为正值,说明位移方向与规定的正方向相同;若位移的计算结果为负值,说明位移方向与规定的正方向相反。
3
对位移公式的理解
① 当v0=0时,s= ,即由静止开始的匀加速直线运动,位移s与t2成正比。
② 当a=0时,s=v0t,即匀速直线运动的位移公式。
注 意
逆向思维法:末速度为 0 的匀减速直线运动可视为反方向的初速度为 0 的匀加速直线运动。
4
位移与时间关系的两种特殊形式
t/s 0 1 2 3 4 5 6
s(m)
因为小车初速度为0,加速度为2m/s2,根据x=at2可求出汽车的位移。
以第二章第1节图2-1所示的汽车运动为例。
0
2
4
9
16
25
36
选汽车行驶的时间t为横坐标,汽车相对起点位置的位移s为纵坐标,分别在坐标纸上描出相应的点,再将各点用平滑曲线连接起来。
t/s
s/m
o
1
2
3
4
5
6
5
10
15
20
25
5
匀变速直线运动的s-t图像
t/s
s/m
o
1
2
3
4
5
6
5
10
15
20
25
从s-t图像中我们可直观看出物体运动过程中位移随时间的变化情况,并可求出不同时间内物体运动的位移。
注意:s-t图象不是物体运动的轨迹,而是位移随时间变化的规律。
a不变
位移
v=v0+at
?
时间
位移
速度
速度时间关系
位移时间关系
速度位移关系
s
如图所示,狙击步枪射击时,若把子弹在枪筒中的运动看作是匀加速直线运动,假设枪筒长s,子弹的加速度为a.
(1)如何求出子弹射出枪口的速度大小?
(2)在上面问题中,已知条件和所求的结果都不涉及时间t,它只是一个中间量,能否将两个公式联立,消去t,只用一个关系式表示位移s与速度vt的关系呢?
02 匀变速直线运动的位移-速度关系
(2)位移与时间的关系式:s=v0t+ at2
速度与时间的关系式:vt= v0 +at
将上述两个公式联立求解,消去时间 t 可得到
v2-v02=2as
(1)由s=at2,vt=at得vt=
公式意义
适用范围
优点
矢量性
两种特 殊形式
速度与位移的关系
匀变速直线运动
该式不涉及时间,研究的问题中若不涉及时间,利用该式求解更加方便
其中的s、v、v0、a都是矢量,应用时必须选取统一的正方向。
若选初速度v0的方向为正方向:
(1)物体做匀加速直线运动,a取正值;
(2)物体做匀减速直线运动,a取负值
(1)当v0=0时,v2=2as→初速度为零的匀加速直线运动;
(2)当v=0时,-v02=2as→末速度为零的匀减速直线运动。
例题:汽车从开始制动到停止所行驶的距离,是衡量汽车制动性能的参数之一。某型号的汽车以100 km/h的速度在柏油路面上行驶,急刹车后做匀减速直线运动。若匀减速时的加速度大小为5m/s2,开始制动后2s内汽车行驶的距离是多少?从开始制动到完全停止,汽车行驶的距离是多少?
[分析]汽车刹车后做匀减速直线运动,运动过程如图所示。在第一问中,已知初速度、加速度和时间的信息求位移,可用位移-时间关系式;在第二问中,通过初速度、加速度和末速度的信息求位移,可用位移-速度关系式。
解:选定初速度方向为正方向,由题意知v0=100 km/h=27.8 m/s,a=-5 m/s2,vt=0,t=2 s
根据速度公式vt=v0+at,可知汽车刹车时间
因为t
(1)刹车类问题一般视为匀减速直线运动,汽车停下后不能做反向的运动。
(2)处理该类问题时,首先要判断刹车后经多长时间速度变为零(即刹车时间)。
①若所给时间大于刹车时间,则v=0,s=v0t0+,t0为刹车时间或s=-。
②若所给时间小于刹车时间,则v=v0+at,s=v0t+at2,t为所给时间。
1.100m决赛中,某运动员的起跑反应时间是0.170s,加速过程可以看成匀加速直线运动,加速时间约为2.5s,最大速度约为12m/s,则该运动员在加速阶段的加速度与位移约为( )
A.4.8m/s2 16m B.4.8m/s2 15m
C.4.5m/s2 16m D.4.5m/s2 15m
B
2.一物体以2 m/s的初速度做匀加速直线运动,4 s内的位移为16 m,则 ( )
A.物体的加速度大小为2 m/s2
B.物体在4 s内的平均速度大小为6 m/s
C.物体在4 s末的瞬时速度大小为6 m/s
D.物体在第2 s内的位移大小为6 m
C
3.如图所示,70周年国庆国旗时,国歌从响起到结束的时间是48s,国旗上升的高度是17.6m。国歌响起同时国旗开始向上做匀加速运动4s,然后匀速运动,最后匀减速运动4s到达旗杆顶端,速度恰好为零,此时国歌结束。求:
(1)国旗匀加速运动的加速度大小。
(2)国旗匀速运动时的速度大小。
解:由题意知,国旗匀加速上升时间t1=4s,匀减速上升时间t3=4s,匀速上升时间t2=t总-t1-t3=40s,
对于国旗加速上升阶段:s1=
对于国旗匀速上升阶段v=a1t1,s2=vt2
对于国旗减速上升阶段:s3=vt3-
根据运动对称性,对于全过程:a1=a2
s1+s2+s3=17.6m
由以上各式可得a1=0.1m/s2;v=0.4m/s。
位移的变化规律
v-t图象所围面积的意义
位移-时间公式x=v0t+ at2的推导和应用
速度-位移公式v2–v02 =2ax的推导和应用
同课章节目录
- 绪论 撩开物理学的神秘面纱
- 一、源自然之问
- 二、探万物之秘
- 三、采科学之益
- 四、启智慧之迪
- 第1章 运动的描述
- 第1节 空间和时间
- 第2节 质点和位移
- 第3节 速度
- 第4节 加速度
- 第2章 匀变速直线运动
- 第1节 速度变化规律
- 第2节 位移变化规律
- 第3节 实验中的误差和有效数字
- 第4节 科学测量:做直线运动物体的瞬时速度
- 第5节 自由落体运动
- 第3章 相互作用
- 第1节 重力与重心
- 第2节 科学探究:弹力
- 第3节 摩擦力
- 第4章 力与平衡
- 第1节 科学探究:力的合成
- 第2节 力的分解
- 第3节 共点力的平衡
- 第5章 牛顿运动定律
- 第1节 牛顿第一运动定律
- 第2节 科学探究:加速度与力、质量的关系
- 第3节 牛顿第二运动定律
- 第4节 牛顿第三运动定律
- 第5节 超重与失重
