1.2 动量守恒定律及其应用(27张PPT)课件 2024-2025学年高二物理鲁科版(2019)选择性必修第一册
文档属性
| 名称 | 1.2 动量守恒定律及其应用(27张PPT)课件 2024-2025学年高二物理鲁科版(2019)选择性必修第一册 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-08-08 09:26:25 | ||
图片预览








文档简介
(共27张PPT)
第一章 动量及其守恒定律
第2节 动量守恒定律及其应用
在连续的敲打下,平板车会怎样运动呢?
在冰壶比赛中,一只冰壶撞击另一只冰壶后,两只冰壶的运动状态都将发生变化,
这种碰撞类运动有什么规律?
1.知道系统、内力、外力的概念。
2.理解动量守恒定律的内容,理解其守恒的条件。
3.会用动量守恒定律解决碰撞问题。
4. 知道反冲现象的特点。
两个穿滑冰鞋的同学静止站在溜冰场上,不论谁推对方,两人都会向相反方向滑去,在推动前,两人的动量都为0; 推动后,每个人 的动量都主生了变化。那么,他们的总动量在推动前后是否也发生了变化呢
01 动量守恒定律
实验与探究:
动量变化规律的实验探索
两个质量相等且带有弹片的滑块装上相同的遮光板,放置在气垫导轨的中部。将两滑块靠在一起并压缩弹片,用细线把它们拴住,两滑块处于停止状忘。烧断细钱,两滑就被弹片弹开后朝相反方向做匀速运动,测量遮光板通过光电门的时间,计算滑块的速度。在两滑块弹开前后,它们的总动量变化了吗
增加其中一个滑块的质量,使其质量是另一个的2倍,重复以上实验。两滑块在弹开前后的总动量会发生变化吗?
实验结果表明,在气垫导轨上,元论两滑块的质量是杏相等,它们在被弹开前的总动 量为 0 ,弹开后的总动量也几乎为0。这说明气垫导轨上的两滑块在相互作用前后的总动量几乎是不变的。
1.内容:一个系统不受外力或者所受合外力为 0 时,这个系统的总动量保持不变。这称为动量守恒定律。
思考:小船停靠湖边时,如果船还未拴住,人便匆匆上岸,人有可能会掉入水中。为什 么会出现这种情况 试用动量守恒定律解释,并与同学讨论交流。
解答:如果船还未拴住,那么在人跳上岸的过程,忽略水对船的阻力作用,人与船组成的系统满足动量守恒。人起跳后,在人获得一个指向岸边的速度的同时,船将获得一个远离岸边是速度。如果人仍按照固定的经验起跳,人就有可能会掉入水中。
2.通过动量定理进行推导动量守恒定律
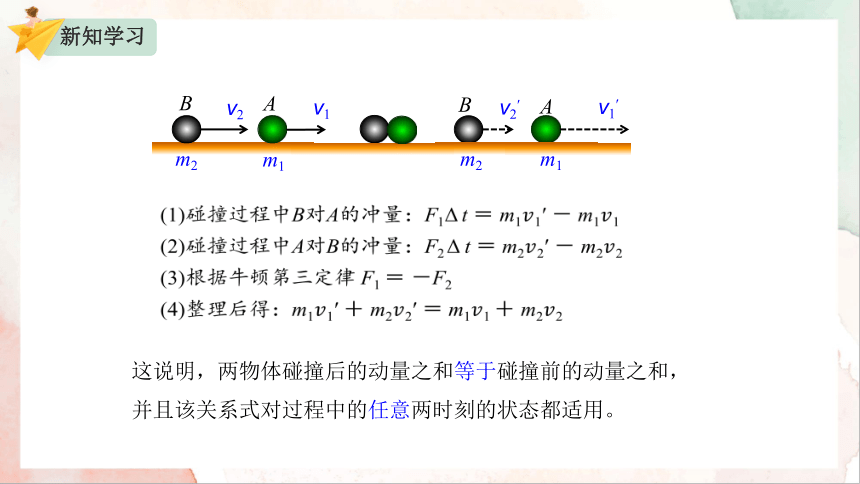
如图在光滑水平桌面上做匀速运动的两个小球A、B,质量分别是m1和m2,沿同一直线向同一方向运动,速度分别是 1 和2 ,2 >1。当B追上A时发生碰撞。碰撞后A、B的速度分别是 1′和2′ 。碰撞过程中A所受B对它的作用力是 F1,B所受A对它的作用力是 F2。碰撞时,两物体之间力的作用时间很短,用 Δ t 表示。
v2
v1
v2′
v1′
m2
m2
m1
m1
B
A
A
B
(1)碰撞过程中B对A的冲量:F1Δ t = m11′ - m11
(2)碰撞过程中A对B的冲量:F2 Δ t = m22′ - m22
(3)根据牛顿第三定律 F1 = -F2
(4)整理后得:m11′ m22′ = m11 m22
v2
v1
v2′
v1′
m2
m2
m1
m1
B
A
A
B
这说明,两物体碰撞后的动量之和等于碰撞前的动量之和,并且该关系式对过程中的任意两时刻的状态都适用。
v2
v1
v2′
v1′
m2
m2
m1
m1
B
A
A
B
N2
N1
G2
G1
F2
F1
那么,碰撞前后满足动量之和不变的两个物体的受力情况是怎样的呢?
两个碰撞的物体在所受外部对它们的作用力的矢量和为0的情况下动量守恒。
内力:系统中物体间的作用力叫做内力。
外力:系统以外的物体施加给系统内物体的力,叫做外力。
3.动量守恒定律内容:如果一个系统不受外力,或者所受外力的矢量和为0,这个系统的总动量保持不变。
4.表达式:
(1) p=p′,系统相互作用前的总动量 p 等于相互作用后的总动量 p′
(2) m1v1+m2v2=m1v1′+m2v2′,相互作用的两个物体组成的系统,作用前的动量和等于作用后的动量和。
(3) Δp1=-Δp2,相互作用的两个物体动量的增量等大反向。
(4) Δp=0,系统总动量的增量为零。
5.适用条件
(1)系统不受外力;(理想条件)
在光滑水平面上有两个载有磁铁的相对运动的小车,
两小车组成的系统动量守恒么?
N2
G2
N1
G1
F1
F2
两小车在运动过程中,相互排斥的磁力属于内力,整个系统的外力即重力和支持力的和为零,所以系统动量守恒。
(2)系统受到外力,但外力的合力为零;(实际条件)
(3)系统所受合外力虽然不为零,但系统的内力远大于外力时,如碰撞、爆炸等现象中,系统的动量可看成近似守恒;
(4)系统所受合外力不为 0,但在某一方向上受到的合外 力为 0,则在该方向上系统的总动量仍然守恒
例题:冬季雨雪天气时,公路上容易发生交通事故。在结冰的公路上,一辆质量为 1.8 X 103 kg的轻型货车尾随另一辆质量为1.2 X 103 kg 的轿车同向行驶,因货车未及时刹车而发生追尾(即碰撞)。若追尾前瞬间货车速度大小为 36 km/h ,轿车速度大小为 18km/h,刚追尾后两车视为紧靠在一起,此时两车的速度多大
分析:以两车组成的系统为研究对象,该系统受到的外力有重力、支持力和摩擦力。由于碰 撞时间很短,碰撞过程中系统所受合外力通常远小于系统内力,可近似认为在该碰撞过程 中系统动量守恒。根据动量守恒定律,可求出两车的共同速度。
解:设货车质量为 m1,轿车质量为m2,碰撞前货车速度为v1、轿车速度为v2,碰撞后两车速度为 v。选定两车碰撞前的速度方向为正方向
由题意可知, m1 = 1.8 10 3kg ,m2 = 1.2 103kg, v1=36km/h, v2=18km/h
由动量守恒定律得m1v1 + m2v2 =(m1 + m2)v
=28.8km/h
所以,刚追尾后两车的速度为 28.8 km/h。
⑴找:找研究对象(系统包括那几个物体)和研究过程;
⑵析:进行受力分析,判断系统动量是否守恒(或在某一方向是否守恒);
⑶定:规定正方向,确定初末状态动量正负号;
⑷列:由动量守恒定律列方程;
⑸解:解方程,得出最后的结果,并对结果进行分析。
应用动量守恒定律解题的基本步骤和方法
拓展:斜碰中的动量守恒
以上讨论的碰撞都是一维碰撞,即碰撞前后的速 度方向均在同一直线上,也称为正碰或对心碰撞。如果碰撞前后的速度方向不在同一直线上,这种碰撞 称为斜碰。
在图 所示的台球斜碰中,可把两王树见为一个 系统,在碰撞过程中,两球相互作用的内力远大于它们受到的外力,因此可近似认为系统的动量守恒。
动量守恒表示系统动量的大小和方向都不变,系统的动量在
各方向的分量也是守恒的。对于有的斜碰,即使整个系统的
总动量不守 恒,也有可能在某方向上的分量是守恒的,人们
常常利用这些特点解决问题。
1.将气球充气后松口释放,气球会沿与喷气方向相反的方向飞去。喷出的空气具有动量,由动量守恒定律可知,气球要向相反方向运动,这就是一种反冲运动。
2.要 点:
b. 一个物体分为两个部分
内力作用下
c. 两部分运动方向相反
02 反冲运动与火箭
3.物理原理:
作用前:P = 0
作用后: P' = m v + M V
则根据动量守恒定律有: P' = P
即 m v + M V = 0 故有:V = ( m / M ) v
负号就表示作用后的两部分运动方向相反
遵循动量守恒定律
4.反冲现象的应用及防止:
(1)应用:
火箭发射
火箭的飞行应用了反冲的原理,靠喷出气流的反冲作用来获得巨大速度。当火箭推进剂燃烧时,从尾部喷出的气体具有很大的动量,火箭获得大小相等、方向相反的动量,因而发生连续的反冲现象,随着燃料的消耗,火箭质量减小,加速度增大,当燃料完全消耗后,火箭即以获得的速度沿着预定轨道飞行。
用步枪射击时要把枪身抵在肩部,以减少反冲的影响
(2)防止:
炮弹射击时要固定好后座
1.一物体从A点运动到B点的过程中,其末动能变为初动能的8倍,下列判断正确的是( )
A.物体的动量可能不变
B.物体的末动量大小变为初动量大小的2倍
C.物体的末动量变为初动量的16倍
D.物体的初动量和末动量的方向一定相同
B
2. 如图所示,光滑水平面上两玩具小车中间夹一压缩了的轻弹簧,两手分别按住小车,使它们静止,对两车及弹簧组成的系统,下列说法中正确的是( )
D
A.两手同时放开后,系统总动量始终为非零的某一数值
B.先放开左手,后放开右手,之后动量不守恒
C.先放开左手,后放开右手,总动量向右
D.无论何时放手,两手放开后的过程中,系统总动量都保持不变,但系统的总动量不一定为零
3.下列所描述的事例或应用中,没有利用反冲原理的是( )
A.喷灌装置的自动旋转
B.章鱼在水中前行和转向
C.运载火箭发射过程
D.码头边轮胎的保护作用
D
4. 如图所示,在光滑水平面上有两个木块A、B,木块B静止,且其上表面左端放置着一小物块C。已知mA=mB=0.2 kg,mC=0.1 kg,现使木块A以初速度v=2 m/s沿水平方向向右滑动,木块A与B相碰后具有共同速度(但不粘连),C与A、B间均有摩擦。求:
(1)木块A与B相碰瞬间木块A的速度及小物块C的速度大小;
(2)若木块A足够长,小物块C的最终速度。
解:(1)木块A与B相碰过程,A与B组成的系统动量守恒,则有,解得=1 m/s。
小物块C的速度为0。
(2)C滑上A后,摩擦力使C加速、使A减速,直至A、C具有共同速度,以A、C为系统,由动量守恒定律得,
解得= m/s。
1.定律内容:一个系统不受外力或者所受合外力为 0 时,这个系统的总动量保持不变。这称为动量守恒定律
2.公式表达:
3.反冲运动与火箭
(2) m1v1+m2v2=m1v1′+m2v2′
(3) Δp1=-Δp2
(4) Δp=0
(1) p=p′
第一章 动量及其守恒定律
第2节 动量守恒定律及其应用
在连续的敲打下,平板车会怎样运动呢?
在冰壶比赛中,一只冰壶撞击另一只冰壶后,两只冰壶的运动状态都将发生变化,
这种碰撞类运动有什么规律?
1.知道系统、内力、外力的概念。
2.理解动量守恒定律的内容,理解其守恒的条件。
3.会用动量守恒定律解决碰撞问题。
4. 知道反冲现象的特点。
两个穿滑冰鞋的同学静止站在溜冰场上,不论谁推对方,两人都会向相反方向滑去,在推动前,两人的动量都为0; 推动后,每个人 的动量都主生了变化。那么,他们的总动量在推动前后是否也发生了变化呢
01 动量守恒定律
实验与探究:
动量变化规律的实验探索
两个质量相等且带有弹片的滑块装上相同的遮光板,放置在气垫导轨的中部。将两滑块靠在一起并压缩弹片,用细线把它们拴住,两滑块处于停止状忘。烧断细钱,两滑就被弹片弹开后朝相反方向做匀速运动,测量遮光板通过光电门的时间,计算滑块的速度。在两滑块弹开前后,它们的总动量变化了吗
增加其中一个滑块的质量,使其质量是另一个的2倍,重复以上实验。两滑块在弹开前后的总动量会发生变化吗?
实验结果表明,在气垫导轨上,元论两滑块的质量是杏相等,它们在被弹开前的总动 量为 0 ,弹开后的总动量也几乎为0。这说明气垫导轨上的两滑块在相互作用前后的总动量几乎是不变的。
1.内容:一个系统不受外力或者所受合外力为 0 时,这个系统的总动量保持不变。这称为动量守恒定律。
思考:小船停靠湖边时,如果船还未拴住,人便匆匆上岸,人有可能会掉入水中。为什 么会出现这种情况 试用动量守恒定律解释,并与同学讨论交流。
解答:如果船还未拴住,那么在人跳上岸的过程,忽略水对船的阻力作用,人与船组成的系统满足动量守恒。人起跳后,在人获得一个指向岸边的速度的同时,船将获得一个远离岸边是速度。如果人仍按照固定的经验起跳,人就有可能会掉入水中。
2.通过动量定理进行推导动量守恒定律
如图在光滑水平桌面上做匀速运动的两个小球A、B,质量分别是m1和m2,沿同一直线向同一方向运动,速度分别是 1 和2 ,2 >1。当B追上A时发生碰撞。碰撞后A、B的速度分别是 1′和2′ 。碰撞过程中A所受B对它的作用力是 F1,B所受A对它的作用力是 F2。碰撞时,两物体之间力的作用时间很短,用 Δ t 表示。
v2
v1
v2′
v1′
m2
m2
m1
m1
B
A
A
B
(1)碰撞过程中B对A的冲量:F1Δ t = m11′ - m11
(2)碰撞过程中A对B的冲量:F2 Δ t = m22′ - m22
(3)根据牛顿第三定律 F1 = -F2
(4)整理后得:m11′ m22′ = m11 m22
v2
v1
v2′
v1′
m2
m2
m1
m1
B
A
A
B
这说明,两物体碰撞后的动量之和等于碰撞前的动量之和,并且该关系式对过程中的任意两时刻的状态都适用。
v2
v1
v2′
v1′
m2
m2
m1
m1
B
A
A
B
N2
N1
G2
G1
F2
F1
那么,碰撞前后满足动量之和不变的两个物体的受力情况是怎样的呢?
两个碰撞的物体在所受外部对它们的作用力的矢量和为0的情况下动量守恒。
内力:系统中物体间的作用力叫做内力。
外力:系统以外的物体施加给系统内物体的力,叫做外力。
3.动量守恒定律内容:如果一个系统不受外力,或者所受外力的矢量和为0,这个系统的总动量保持不变。
4.表达式:
(1) p=p′,系统相互作用前的总动量 p 等于相互作用后的总动量 p′
(2) m1v1+m2v2=m1v1′+m2v2′,相互作用的两个物体组成的系统,作用前的动量和等于作用后的动量和。
(3) Δp1=-Δp2,相互作用的两个物体动量的增量等大反向。
(4) Δp=0,系统总动量的增量为零。
5.适用条件
(1)系统不受外力;(理想条件)
在光滑水平面上有两个载有磁铁的相对运动的小车,
两小车组成的系统动量守恒么?
N2
G2
N1
G1
F1
F2
两小车在运动过程中,相互排斥的磁力属于内力,整个系统的外力即重力和支持力的和为零,所以系统动量守恒。
(2)系统受到外力,但外力的合力为零;(实际条件)
(3)系统所受合外力虽然不为零,但系统的内力远大于外力时,如碰撞、爆炸等现象中,系统的动量可看成近似守恒;
(4)系统所受合外力不为 0,但在某一方向上受到的合外 力为 0,则在该方向上系统的总动量仍然守恒
例题:冬季雨雪天气时,公路上容易发生交通事故。在结冰的公路上,一辆质量为 1.8 X 103 kg的轻型货车尾随另一辆质量为1.2 X 103 kg 的轿车同向行驶,因货车未及时刹车而发生追尾(即碰撞)。若追尾前瞬间货车速度大小为 36 km/h ,轿车速度大小为 18km/h,刚追尾后两车视为紧靠在一起,此时两车的速度多大
分析:以两车组成的系统为研究对象,该系统受到的外力有重力、支持力和摩擦力。由于碰 撞时间很短,碰撞过程中系统所受合外力通常远小于系统内力,可近似认为在该碰撞过程 中系统动量守恒。根据动量守恒定律,可求出两车的共同速度。
解:设货车质量为 m1,轿车质量为m2,碰撞前货车速度为v1、轿车速度为v2,碰撞后两车速度为 v。选定两车碰撞前的速度方向为正方向
由题意可知, m1 = 1.8 10 3kg ,m2 = 1.2 103kg, v1=36km/h, v2=18km/h
由动量守恒定律得m1v1 + m2v2 =(m1 + m2)v
=28.8km/h
所以,刚追尾后两车的速度为 28.8 km/h。
⑴找:找研究对象(系统包括那几个物体)和研究过程;
⑵析:进行受力分析,判断系统动量是否守恒(或在某一方向是否守恒);
⑶定:规定正方向,确定初末状态动量正负号;
⑷列:由动量守恒定律列方程;
⑸解:解方程,得出最后的结果,并对结果进行分析。
应用动量守恒定律解题的基本步骤和方法
拓展:斜碰中的动量守恒
以上讨论的碰撞都是一维碰撞,即碰撞前后的速 度方向均在同一直线上,也称为正碰或对心碰撞。如果碰撞前后的速度方向不在同一直线上,这种碰撞 称为斜碰。
在图 所示的台球斜碰中,可把两王树见为一个 系统,在碰撞过程中,两球相互作用的内力远大于它们受到的外力,因此可近似认为系统的动量守恒。
动量守恒表示系统动量的大小和方向都不变,系统的动量在
各方向的分量也是守恒的。对于有的斜碰,即使整个系统的
总动量不守 恒,也有可能在某方向上的分量是守恒的,人们
常常利用这些特点解决问题。
1.将气球充气后松口释放,气球会沿与喷气方向相反的方向飞去。喷出的空气具有动量,由动量守恒定律可知,气球要向相反方向运动,这就是一种反冲运动。
2.要 点:
b. 一个物体分为两个部分
内力作用下
c. 两部分运动方向相反
02 反冲运动与火箭
3.物理原理:
作用前:P = 0
作用后: P' = m v + M V
则根据动量守恒定律有: P' = P
即 m v + M V = 0 故有:V = ( m / M ) v
负号就表示作用后的两部分运动方向相反
遵循动量守恒定律
4.反冲现象的应用及防止:
(1)应用:
火箭发射
火箭的飞行应用了反冲的原理,靠喷出气流的反冲作用来获得巨大速度。当火箭推进剂燃烧时,从尾部喷出的气体具有很大的动量,火箭获得大小相等、方向相反的动量,因而发生连续的反冲现象,随着燃料的消耗,火箭质量减小,加速度增大,当燃料完全消耗后,火箭即以获得的速度沿着预定轨道飞行。
用步枪射击时要把枪身抵在肩部,以减少反冲的影响
(2)防止:
炮弹射击时要固定好后座
1.一物体从A点运动到B点的过程中,其末动能变为初动能的8倍,下列判断正确的是( )
A.物体的动量可能不变
B.物体的末动量大小变为初动量大小的2倍
C.物体的末动量变为初动量的16倍
D.物体的初动量和末动量的方向一定相同
B
2. 如图所示,光滑水平面上两玩具小车中间夹一压缩了的轻弹簧,两手分别按住小车,使它们静止,对两车及弹簧组成的系统,下列说法中正确的是( )
D
A.两手同时放开后,系统总动量始终为非零的某一数值
B.先放开左手,后放开右手,之后动量不守恒
C.先放开左手,后放开右手,总动量向右
D.无论何时放手,两手放开后的过程中,系统总动量都保持不变,但系统的总动量不一定为零
3.下列所描述的事例或应用中,没有利用反冲原理的是( )
A.喷灌装置的自动旋转
B.章鱼在水中前行和转向
C.运载火箭发射过程
D.码头边轮胎的保护作用
D
4. 如图所示,在光滑水平面上有两个木块A、B,木块B静止,且其上表面左端放置着一小物块C。已知mA=mB=0.2 kg,mC=0.1 kg,现使木块A以初速度v=2 m/s沿水平方向向右滑动,木块A与B相碰后具有共同速度(但不粘连),C与A、B间均有摩擦。求:
(1)木块A与B相碰瞬间木块A的速度及小物块C的速度大小;
(2)若木块A足够长,小物块C的最终速度。
解:(1)木块A与B相碰过程,A与B组成的系统动量守恒,则有,解得=1 m/s。
小物块C的速度为0。
(2)C滑上A后,摩擦力使C加速、使A减速,直至A、C具有共同速度,以A、C为系统,由动量守恒定律得,
解得= m/s。
1.定律内容:一个系统不受外力或者所受合外力为 0 时,这个系统的总动量保持不变。这称为动量守恒定律
2.公式表达:
3.反冲运动与火箭
(2) m1v1+m2v2=m1v1′+m2v2′
(3) Δp1=-Δp2
(4) Δp=0
(1) p=p′
同课章节目录
- 第1章 动量及其守恒定律
- 第1节 动量和动量定理
- 第2节 动量守恒定律及其应用
- 第3节 科学验证:动量守恒定律
- 第4节 弹性碰撞与非弹性碰撞
- 第2章 机械振动
- 第1节 简谐运动
- 第2节 振动的描述
- 第3节 单摆
- 第4节 科学测量:用单摆测量重力加速度
- 第5节 生活中的振动
- 第3章 机械波
- 第1节 波的形成和描述
- 第2节 波的反射和折射
- 第3节 波的干涉和衍射
- 第4节 多普勒效应及其应用
- 第4章 光的折射和全反射
- 第1节 光的折射
- 第2节 科学测量:玻璃的折射率
- 第3节 光的全反射
- 第4节 光导纤维及其应用
- 第5章 光的干涉、衍射和偏振
- 第1节 光的干涉
- 第2节 科学测量:用双缝干涉测光的波长
- 第3节 光的衍射
- 第4节 光的偏振
- 第5节 激光与全息照相
