1.2 动量守恒定律及其应用(25张PPT)课件 2024-2025学年高二物理鲁科版(2019)选择性必修第一册
文档属性
| 名称 | 1.2 动量守恒定律及其应用(25张PPT)课件 2024-2025学年高二物理鲁科版(2019)选择性必修第一册 |  | |
| 格式 | pptx | ||
| 文件大小 | 6.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-08-08 09:27:12 | ||
图片预览







文档简介
(共25张PPT)
第一章 动量和动量定理
第2节 动量守恒定律及其应用
生活中的碰撞现象
这些不同的碰撞现象中是否隐藏着相同的物理规律?
1.知道系统、内力、外力的概念。
2.理解动量守恒定律的内容,理解其守恒的条件。
3.会用动量守恒定律解决碰撞问题。
4. 知道反冲现象的特点,了解火箭飞行原理。
实验与探究:研究气垫导轨上滑块碰撞时的动量守恒
实验器材:气垫导轨、光电计时器、天平、滑块(两个)、弹簧片、细绳、弹性碰撞架、胶布、撞针、橡皮泥等。
实验设计:利用气垫导轨使两滑块发生一维碰撞,如图所示:
1. 质量的测量:用天平测量。
2. 速度的测量: ,式中 Δx 为滑块上挡光片的宽度, Δt 为数字计时器显示的滑块上挡光片经过光电门的时间。
实验步骤:
1.两个质量相等且带有弹片的滑块装上相同的遮光板,放置在气垫导轨的中部。将两滑块靠在一起并压缩弹片,用细线把它们拴住,两滑块处于静止状态。烧断细线,两滑块被弹片弹开后朝相反方向做匀速运动。测量遮光板通过光电门的时间,计算滑块的速度。
2.增加其中一个滑块的质量,使其质量是另一个的2倍,重复以上实验
实验结果:
在气垫导轨上,无论两滑块的质量是否相等,它们在被弹开前的总动量为零,弹开后的总动量也几乎为零。这说明气垫导轨上的两滑块在相互作用前后的总动量几乎是不变的。
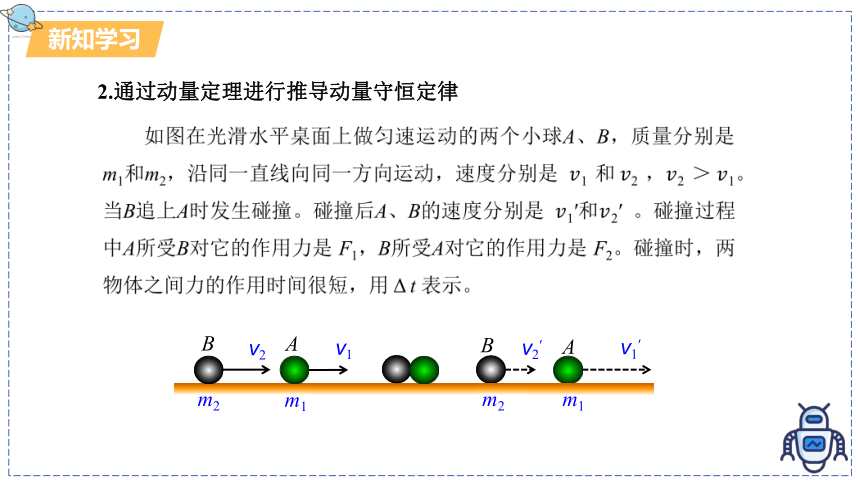
2.通过动量定理进行推导动量守恒定律
如图在光滑水平桌面上做匀速运动的两个小球A、B,质量分别是m1和m2,沿同一直线向同一方向运动,速度分别是 1 和2 ,2 >1。当B追上A时发生碰撞。碰撞后A、B的速度分别是 1′和2′ 。碰撞过程中A所受B对它的作用力是 F1,B所受A对它的作用力是 F2。碰撞时,两物体之间力的作用时间很短,用 Δ t 表示。
v2
v1
v2′
v1′
m2
m2
m1
m1
B
A
A
B
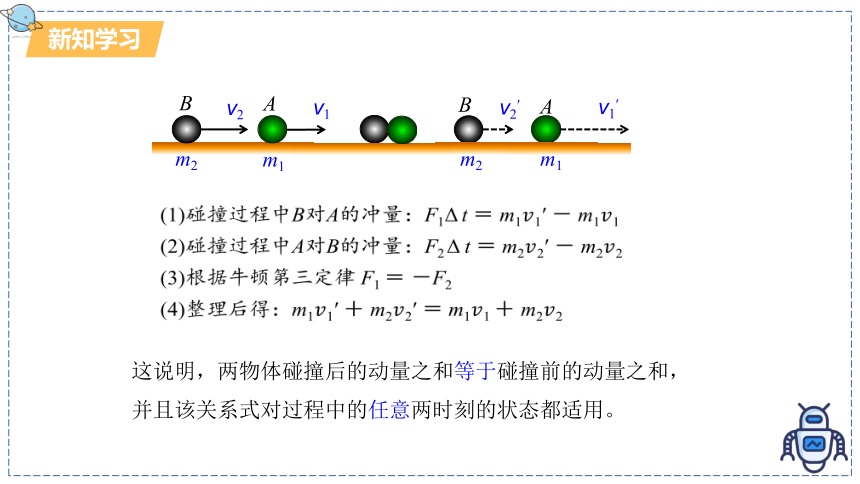
(1)碰撞过程中B对A的冲量:F1Δ t = m11′ - m11
(2)碰撞过程中A对B的冲量:F2 Δ t = m22′ - m22
(3)根据牛顿第三定律 F1 = -F2
(4)整理后得:m11′ m22′ = m11 m22
v2
v1
v2′
v1′
m2
m2
m1
m1
B
A
A
B
这说明,两物体碰撞后的动量之和等于碰撞前的动量之和,并且该关系式对过程中的任意两时刻的状态都适用。
v2
v1
v2′
v1′
m2
m2
m1
m1
B
A
A
B
N2
N1
G2
G1
F2
F1
那么,碰撞前后满足动量之和不变的两个物体的受力情况是怎样的呢?
两物体各自既受到对方的作用力,同时又受到重力和桌面的支持力,重力和支持力是一对平衡力。两个碰撞的物体在所受外部对它们的作用力的矢量和为0的情况下动量守恒。
系统、内力、外力
1.系统:一般而言,碰撞、爆炸等现象的研究对象是两个(或多个)物体。我们把由两个(或多个)相互作用的物体构成的整体叫作一个力学系统,简称系统。
2.内力:系统中物体间的作用力,叫作内力。
3.外力:系统以外的物体施加给系统内物体的力,叫作外力。
知识点一:动量守恒定律
1. 内容:如果一个系统不受外力,或者所受外力的矢量和为0,这个系统的总动量保持不变,这就是动量守恒定律。
2.动量守恒定律的表达式:
① p = p′ (系统相互作用前的总动量 p 等于相互作用后的总动量 p′ )
② Δ p= 0(系统总动量的增量为0)
③ Δ p1 =-Δ p2 (两个物体组成的系统中,各自动量的增量大小相等、方向相反)
④ m1v1 + m2v2 = m1v1′ + m2v2′ (两个物体组成的系统中,相互作用前两个物体的总动量等于相互作用后两个物体的总动量)
(1)系统不受外力或外力的矢量和为零,系统动量守恒;
3.成立条件
(2) 系统所受合外力虽然不为零,但系统的内力远大于外力时,
如碰撞、爆炸等现象中,系统的动量可看成近似守恒;
(3)系统所受的合外力不为零,但某一方向上合外力为零,则系统在这一方向上动量守恒。
思考:斜面B置于光滑水平面上,物体A沿光滑斜面滑下,则AB组成的系统受到几个作用力?
哪些力是内力?哪些力是外力?
系统动量守恒吗?
竖直方向失重:N<(M+m)g ,系统动量不守恒
水平方向:系统不受外力,动量守恒
N
Mg
mg
N1
N1′
例题:冬季雨雪天气时,公路上容易发生交通事故。在结冰的公路上,一辆质量为 1.8 × 103 kg的轻型货车尾随另一辆质量为1.2 X 103 kg 的轿车同向行驶,因货车未及时刹车而发生追尾(即碰撞)。若追尾前瞬间货车速度大小为 36 km/h ,轿车速度大小为 18km/h,刚追尾后两车视为紧靠在一起,此时两车的速度多大
分析:以两车组成的系统为研究对象,该系统受到的外力有重力、支持力和摩擦力。由于碰 撞时间很短,碰撞过程中系统所受合外力通常远小于系统内力,可近似认为在该碰撞过程 中系统动量守恒。根据动量守恒定律,可求出两车的共同速度。
解:设货车质量为 m1,轿车质量为m2,碰撞前货车速度为v1、轿车速度为v2,碰撞后两车速度为 v。选定两车碰撞前的速度方向为正方向
由题意可知, m1 = 1.8 10 3kg ,m2 = 1.2 103kg, v1=36km/h, v2=18km/h
由动量守恒定律得m1v1 + m2v2 =(m1 + m2)v
=28.8km/h
所以,刚追尾后两车的速度为 28.8 km/h。
应用动量守恒定律解题的思路
明确研究对象,确定系统的组成
受力分析,分清内力、外力,确定动量是否守恒
规定正方向,确定初、末动量
根据动量守恒定律,建立方程
代入数据,求出结果并讨论说明
将气球充气后松口释放,气球会沿着与喷气方向相反的方向飞去
反冲运动
章鱼的运动
火箭的发射
1. 定义:系统在内力作用下,当一部分向某一方向的运动时,剩余部分沿相反方向运动的现象。
知识点二:反冲运动与火箭
(1)物体的不同部分在内力作用下向相反方向运动。
(2)反冲运动和碰撞、爆炸有相似之处,相互作用力常为变力,且作用力大,一般都满足内力 外力,所以反冲运动可用动量守恒定律来处理。
(3)反冲过程中,由于有其他形式的能转化为机械能,所以系统的总动能增加。
2.特点
反冲运动是系统内力作用的结果。在发生反冲运动的过程中,系统所受到的外力远远小于内力,遵循动量守恒定律。
作用前:P = 0
作用后: P' = m1 v 1+ m2 v2
则根据动量守恒定律有: P' = P
即 m1v1 + m2v2 = 0 故有:v2 = ( m1 / m2 ) v1
负号就表示作用后的两部分运动方向相反
3. 反冲运动的原理
4. 反冲现象的应用及防止
(1)反冲现象的应用
灌溉喷水器
礼花燃放
海上冲水
(2)反冲现象的防止
大炮止退犁
步枪射击
枪身的反冲会影响射击的准确性,用步枪射击时要把枪身抵在肩部,以减少反冲的影响。
炮车的履带表面有较深的突起抓地钩型设计和是为了增大摩擦力,止退犁和两个液压缓冲器,都是为了在火炮连射时起到“止退”的作用,提高命中精度而精心设计的。
古代的火箭(模型)
思考:火箭的飞行应用了什么原理,它是靠什么作用来获得巨大速度的?
箭杆上捆了一个前端封闭的火药筒,点燃后生成的燃气以很大速度向后喷出,箭杆由于反冲而向前运动。
1.原理:火箭的飞行应用了反冲的原理,靠喷出气流的反冲作用来获得巨大速度。
当火箭推进剂燃烧时,从尾部喷出的气体具有很大的动量,火箭获得大小相等、方向相反的动量,因而发生连续的反冲现象,随着燃料的消耗,火箭质量减小,加速度增大,当燃料完全消耗后,火箭即以获得的速度沿着预定轨道飞行。
2.结构:为了提高速度,实行多级(不超过四级)火箭发射。
3.作用:发射洲际导弹、人造卫星、宇宙飞船。
1.(多选)关于动量守恒的条件,下面说法正确的是( )
A.只要系统内有摩擦力,动量就不可能守恒
B.只要系统所受合外力为零,系统动量就守恒
C.系统加速度为零,系统动量一定守恒
D.只要系统所受合外力不为零,则系统在任何方向上动量都不可能守恒
BC
2.如图所示,一辆小车静止在光滑的水平面上,小车立柱上固定一条长为 L、系有小球的水平细绳,小球由静止释放,不计一切摩擦,下列说法正确的是( )
A.小球的机械能守恒,动量不守恒
B.小球的机械能不守恒,动量也不守恒
C.球、车系统的机械能守恒,动量守恒
D.球、车系统的机械能守恒,水平方向动量守恒
L
BD
v
m1
m-m1
火箭炸裂前的总动量为
炸裂后的总动量为
根据动量守恒定律可得:
解出
3.一枚在空中飞行的火箭质量为m,在某时刻的速度为v,方向水平,燃料即将耗尽。此时,火箭突然炸裂成两块(如图),其中质量为m1的一块沿着与v相反的方向飞去,速度为v1。求炸裂后另一块的速度v2。
解:炸裂过程中内力远大于外力,炸裂的两部分组成的系统动量守恒。以v方向为正。
第一章 动量和动量定理
第2节 动量守恒定律及其应用
生活中的碰撞现象
这些不同的碰撞现象中是否隐藏着相同的物理规律?
1.知道系统、内力、外力的概念。
2.理解动量守恒定律的内容,理解其守恒的条件。
3.会用动量守恒定律解决碰撞问题。
4. 知道反冲现象的特点,了解火箭飞行原理。
实验与探究:研究气垫导轨上滑块碰撞时的动量守恒
实验器材:气垫导轨、光电计时器、天平、滑块(两个)、弹簧片、细绳、弹性碰撞架、胶布、撞针、橡皮泥等。
实验设计:利用气垫导轨使两滑块发生一维碰撞,如图所示:
1. 质量的测量:用天平测量。
2. 速度的测量: ,式中 Δx 为滑块上挡光片的宽度, Δt 为数字计时器显示的滑块上挡光片经过光电门的时间。
实验步骤:
1.两个质量相等且带有弹片的滑块装上相同的遮光板,放置在气垫导轨的中部。将两滑块靠在一起并压缩弹片,用细线把它们拴住,两滑块处于静止状态。烧断细线,两滑块被弹片弹开后朝相反方向做匀速运动。测量遮光板通过光电门的时间,计算滑块的速度。
2.增加其中一个滑块的质量,使其质量是另一个的2倍,重复以上实验
实验结果:
在气垫导轨上,无论两滑块的质量是否相等,它们在被弹开前的总动量为零,弹开后的总动量也几乎为零。这说明气垫导轨上的两滑块在相互作用前后的总动量几乎是不变的。
2.通过动量定理进行推导动量守恒定律
如图在光滑水平桌面上做匀速运动的两个小球A、B,质量分别是m1和m2,沿同一直线向同一方向运动,速度分别是 1 和2 ,2 >1。当B追上A时发生碰撞。碰撞后A、B的速度分别是 1′和2′ 。碰撞过程中A所受B对它的作用力是 F1,B所受A对它的作用力是 F2。碰撞时,两物体之间力的作用时间很短,用 Δ t 表示。
v2
v1
v2′
v1′
m2
m2
m1
m1
B
A
A
B
(1)碰撞过程中B对A的冲量:F1Δ t = m11′ - m11
(2)碰撞过程中A对B的冲量:F2 Δ t = m22′ - m22
(3)根据牛顿第三定律 F1 = -F2
(4)整理后得:m11′ m22′ = m11 m22
v2
v1
v2′
v1′
m2
m2
m1
m1
B
A
A
B
这说明,两物体碰撞后的动量之和等于碰撞前的动量之和,并且该关系式对过程中的任意两时刻的状态都适用。
v2
v1
v2′
v1′
m2
m2
m1
m1
B
A
A
B
N2
N1
G2
G1
F2
F1
那么,碰撞前后满足动量之和不变的两个物体的受力情况是怎样的呢?
两物体各自既受到对方的作用力,同时又受到重力和桌面的支持力,重力和支持力是一对平衡力。两个碰撞的物体在所受外部对它们的作用力的矢量和为0的情况下动量守恒。
系统、内力、外力
1.系统:一般而言,碰撞、爆炸等现象的研究对象是两个(或多个)物体。我们把由两个(或多个)相互作用的物体构成的整体叫作一个力学系统,简称系统。
2.内力:系统中物体间的作用力,叫作内力。
3.外力:系统以外的物体施加给系统内物体的力,叫作外力。
知识点一:动量守恒定律
1. 内容:如果一个系统不受外力,或者所受外力的矢量和为0,这个系统的总动量保持不变,这就是动量守恒定律。
2.动量守恒定律的表达式:
① p = p′ (系统相互作用前的总动量 p 等于相互作用后的总动量 p′ )
② Δ p= 0(系统总动量的增量为0)
③ Δ p1 =-Δ p2 (两个物体组成的系统中,各自动量的增量大小相等、方向相反)
④ m1v1 + m2v2 = m1v1′ + m2v2′ (两个物体组成的系统中,相互作用前两个物体的总动量等于相互作用后两个物体的总动量)
(1)系统不受外力或外力的矢量和为零,系统动量守恒;
3.成立条件
(2) 系统所受合外力虽然不为零,但系统的内力远大于外力时,
如碰撞、爆炸等现象中,系统的动量可看成近似守恒;
(3)系统所受的合外力不为零,但某一方向上合外力为零,则系统在这一方向上动量守恒。
思考:斜面B置于光滑水平面上,物体A沿光滑斜面滑下,则AB组成的系统受到几个作用力?
哪些力是内力?哪些力是外力?
系统动量守恒吗?
竖直方向失重:N<(M+m)g ,系统动量不守恒
水平方向:系统不受外力,动量守恒
N
Mg
mg
N1
N1′
例题:冬季雨雪天气时,公路上容易发生交通事故。在结冰的公路上,一辆质量为 1.8 × 103 kg的轻型货车尾随另一辆质量为1.2 X 103 kg 的轿车同向行驶,因货车未及时刹车而发生追尾(即碰撞)。若追尾前瞬间货车速度大小为 36 km/h ,轿车速度大小为 18km/h,刚追尾后两车视为紧靠在一起,此时两车的速度多大
分析:以两车组成的系统为研究对象,该系统受到的外力有重力、支持力和摩擦力。由于碰 撞时间很短,碰撞过程中系统所受合外力通常远小于系统内力,可近似认为在该碰撞过程 中系统动量守恒。根据动量守恒定律,可求出两车的共同速度。
解:设货车质量为 m1,轿车质量为m2,碰撞前货车速度为v1、轿车速度为v2,碰撞后两车速度为 v。选定两车碰撞前的速度方向为正方向
由题意可知, m1 = 1.8 10 3kg ,m2 = 1.2 103kg, v1=36km/h, v2=18km/h
由动量守恒定律得m1v1 + m2v2 =(m1 + m2)v
=28.8km/h
所以,刚追尾后两车的速度为 28.8 km/h。
应用动量守恒定律解题的思路
明确研究对象,确定系统的组成
受力分析,分清内力、外力,确定动量是否守恒
规定正方向,确定初、末动量
根据动量守恒定律,建立方程
代入数据,求出结果并讨论说明
将气球充气后松口释放,气球会沿着与喷气方向相反的方向飞去
反冲运动
章鱼的运动
火箭的发射
1. 定义:系统在内力作用下,当一部分向某一方向的运动时,剩余部分沿相反方向运动的现象。
知识点二:反冲运动与火箭
(1)物体的不同部分在内力作用下向相反方向运动。
(2)反冲运动和碰撞、爆炸有相似之处,相互作用力常为变力,且作用力大,一般都满足内力 外力,所以反冲运动可用动量守恒定律来处理。
(3)反冲过程中,由于有其他形式的能转化为机械能,所以系统的总动能增加。
2.特点
反冲运动是系统内力作用的结果。在发生反冲运动的过程中,系统所受到的外力远远小于内力,遵循动量守恒定律。
作用前:P = 0
作用后: P' = m1 v 1+ m2 v2
则根据动量守恒定律有: P' = P
即 m1v1 + m2v2 = 0 故有:v2 = ( m1 / m2 ) v1
负号就表示作用后的两部分运动方向相反
3. 反冲运动的原理
4. 反冲现象的应用及防止
(1)反冲现象的应用
灌溉喷水器
礼花燃放
海上冲水
(2)反冲现象的防止
大炮止退犁
步枪射击
枪身的反冲会影响射击的准确性,用步枪射击时要把枪身抵在肩部,以减少反冲的影响。
炮车的履带表面有较深的突起抓地钩型设计和是为了增大摩擦力,止退犁和两个液压缓冲器,都是为了在火炮连射时起到“止退”的作用,提高命中精度而精心设计的。
古代的火箭(模型)
思考:火箭的飞行应用了什么原理,它是靠什么作用来获得巨大速度的?
箭杆上捆了一个前端封闭的火药筒,点燃后生成的燃气以很大速度向后喷出,箭杆由于反冲而向前运动。
1.原理:火箭的飞行应用了反冲的原理,靠喷出气流的反冲作用来获得巨大速度。
当火箭推进剂燃烧时,从尾部喷出的气体具有很大的动量,火箭获得大小相等、方向相反的动量,因而发生连续的反冲现象,随着燃料的消耗,火箭质量减小,加速度增大,当燃料完全消耗后,火箭即以获得的速度沿着预定轨道飞行。
2.结构:为了提高速度,实行多级(不超过四级)火箭发射。
3.作用:发射洲际导弹、人造卫星、宇宙飞船。
1.(多选)关于动量守恒的条件,下面说法正确的是( )
A.只要系统内有摩擦力,动量就不可能守恒
B.只要系统所受合外力为零,系统动量就守恒
C.系统加速度为零,系统动量一定守恒
D.只要系统所受合外力不为零,则系统在任何方向上动量都不可能守恒
BC
2.如图所示,一辆小车静止在光滑的水平面上,小车立柱上固定一条长为 L、系有小球的水平细绳,小球由静止释放,不计一切摩擦,下列说法正确的是( )
A.小球的机械能守恒,动量不守恒
B.小球的机械能不守恒,动量也不守恒
C.球、车系统的机械能守恒,动量守恒
D.球、车系统的机械能守恒,水平方向动量守恒
L
BD
v
m1
m-m1
火箭炸裂前的总动量为
炸裂后的总动量为
根据动量守恒定律可得:
解出
3.一枚在空中飞行的火箭质量为m,在某时刻的速度为v,方向水平,燃料即将耗尽。此时,火箭突然炸裂成两块(如图),其中质量为m1的一块沿着与v相反的方向飞去,速度为v1。求炸裂后另一块的速度v2。
解:炸裂过程中内力远大于外力,炸裂的两部分组成的系统动量守恒。以v方向为正。
同课章节目录
- 第1章 动量及其守恒定律
- 第1节 动量和动量定理
- 第2节 动量守恒定律及其应用
- 第3节 科学验证:动量守恒定律
- 第4节 弹性碰撞与非弹性碰撞
- 第2章 机械振动
- 第1节 简谐运动
- 第2节 振动的描述
- 第3节 单摆
- 第4节 科学测量:用单摆测量重力加速度
- 第5节 生活中的振动
- 第3章 机械波
- 第1节 波的形成和描述
- 第2节 波的反射和折射
- 第3节 波的干涉和衍射
- 第4节 多普勒效应及其应用
- 第4章 光的折射和全反射
- 第1节 光的折射
- 第2节 科学测量:玻璃的折射率
- 第3节 光的全反射
- 第4节 光导纤维及其应用
- 第5章 光的干涉、衍射和偏振
- 第1节 光的干涉
- 第2节 科学测量:用双缝干涉测光的波长
- 第3节 光的衍射
- 第4节 光的偏振
- 第5节 激光与全息照相
