2.2 课时1 速度与时间的关系(21张PPT)课件 2024-2025学年高一物理粤教版(2019)必修第一册
文档属性
| 名称 | 2.2 课时1 速度与时间的关系(21张PPT)课件 2024-2025学年高一物理粤教版(2019)必修第一册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 粤教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-08-08 00:00:00 | ||
图片预览




文档简介
(共21张PPT)
第二章 匀变速直线运动
第2节 课时1 速度与时间的关系
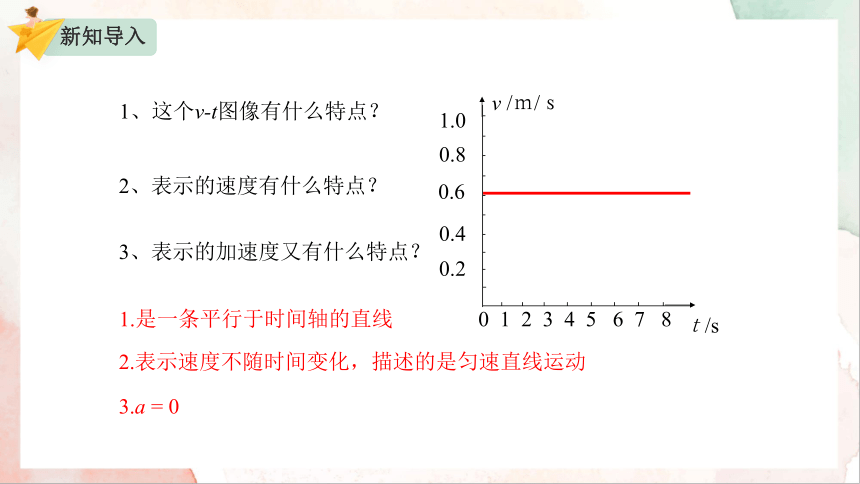
1、这个v-t图像有什么特点?
0 1 2 3 4 5 6 7 8
0.2
0.4
0.6
0.8
1.0
v /m/s
t/s
2、表示的速度有什么特点?
3、表示的加速度又有什么特点?
1.是一条平行于时间轴的直线
2.表示速度不随时间变化,描述的是匀速直线运动
3.a = 0
1.理解匀变速直线运动的v-t图像特点。
2.理解匀变速直线运动的速度公式,并会用公式解决匀变速直线运动问题。
01 速度与时间的关系
1.数学推导
物体开始运动记为0时刻,初速度为v0,t 时刻速度为vt.
v = v 0 + at
v - v 0 = at
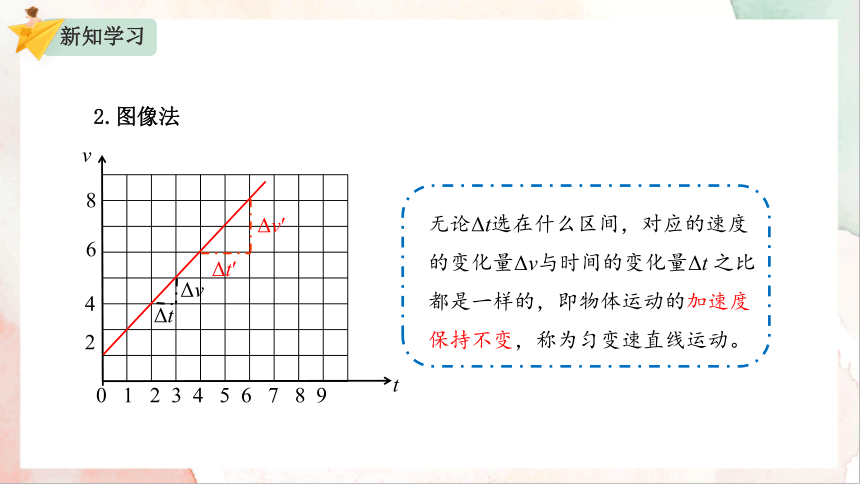
2.图像法
v
t
Δt
Δv
Δt
Δv
0 1 2 3 4 5 6 7 8 9
4 2
6
8
无论Δt选在什么区间,对应的速度的变化量Δv与时间的变化量Δt 之比都是一样的,即物体运动的加速度保持不变,称为匀变速直线运动。
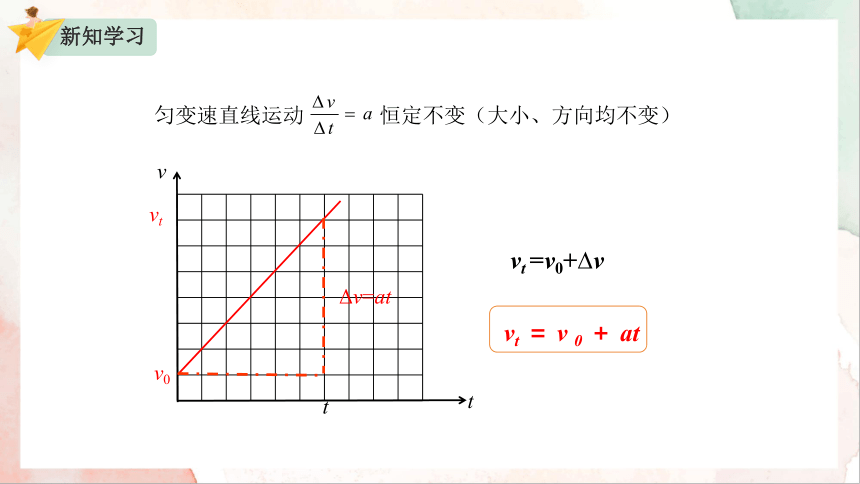
匀变速直线运动 恒定不变(大小、方向均不变)
v
t
v0
Δv=at
vt
t
vt =v0+ v
vt = v 0 + at
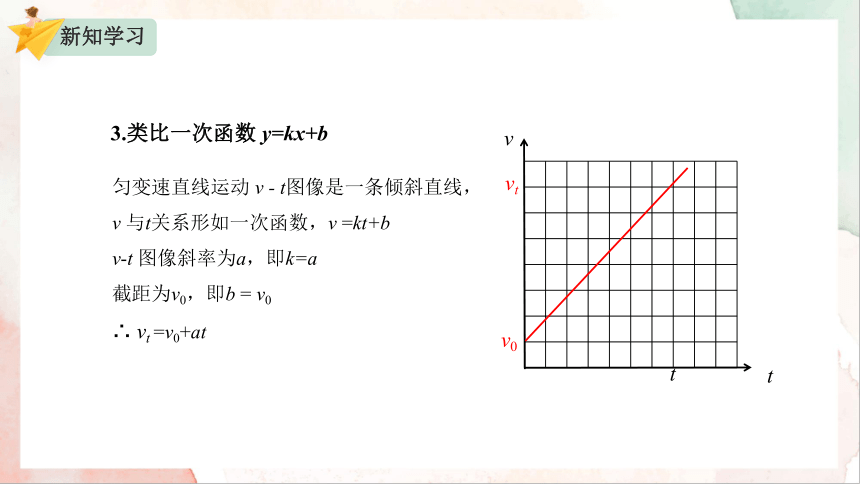
3.类比一次函数 y=kx+b
匀变速直线运动 v - t图像是一条倾斜直线,
v 与t关系形如一次函数,v =kt+b
v-t 图像斜率为a,即k=a
截距为v0,即b = v0
∴ vt =v0+at
v
t
v0
vt
t
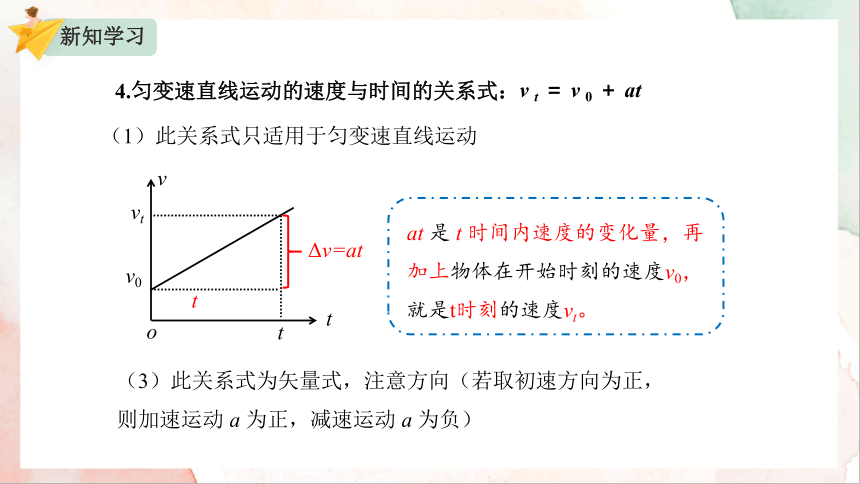
4.匀变速直线运动的速度与时间的关系式:
v t = v 0 + at
at 是 t 时间内速度的变化量,再加上物体在开始时刻的速度v0, 就是t时刻的速度vt。
vt
t
v
t
o
v0
t
Δv=at
(1)此关系式只适用于匀变速直线运动
(3)此关系式为矢量式,注意方向(若取初速方向为正,则加速运动 a 为正,减速运动 a 为负)
(1)当 v 0= 0 时,v t = at
物体做初速度为零的匀加速直线运动
(2)当 a = 0 时, v t = v0
物体做匀速直线运动
5. v t= v 0 + at的特殊形式
讨论与交流1:如图所示是三个质点的v-t图像,图线①②③表示的运动情况是怎样的?图像中图线的交点表示什么含义?
①匀加速直线运动
②匀速直线运动
③匀减速直线运动
当两图线有交点时,
表示两物体在此时刻速度相等。
讨论与交流2:如图所示是某质点运动的v-t图像。试描述该图像与物体运动实际情况的对应关系。请求出该物体每个时间段的加速度。
①在0~1s内,物体做初速度为零的匀加速直线运动至1s末速度为4m/s
③在3~4s内,物体做匀减速直线运动至4s末速度为零
②在1~3s内,物体做匀变速直线运动至3s末速度为-4m/s (在1~2s内,物体做匀减速直线运动至2s末速度为零,2~3s内,物体做反向匀加速直线运动至3s末速度为-4m/s)
①
②
③
例题:一辆汽车以 36 km/h 的速度在平直公路上匀速行驶。从某时刻起,它以 0.6 m/s2的加速度加速,10s 末因故突然紧急刹车,随后汽车停了下来。刹车时做匀减速运动的加速度大小是 6 m/s2 。
(1)汽车在 10 s 末的速度是多少?
(2)汽车从刹车到停下来用了多长时间?
分析:依题意,汽车加速和减速过程都是在做匀变速直线运动。第(1)问是已知加速的时间求末速度。
第(2)问是已知末速度求减速的时间。两个问题都需要用匀变速直线运动的速度与时间关系式来求解。其中,第(2)问汽车加速度的方向跟速度、位移的方向相反,需要建立坐标系处理物理量之间的正负号问题。
解:(1)汽车做匀加速直线运动。
初速度 v0=36 km/h =10 m/s,加速度 a=0.6 m/s2 ,时间 t=10 s根据匀变速直线运动速度与时间的关系式,有
v=v0+at =10 m/s+0.6 m/s2 ×10 s=16 m/s
(2)以汽车运动方向为正方向建立一维坐标系(如图 ),与正方向一致的量取正号,相反的取负号。
v
a
0
x
汽车从第 10 s 末开始做匀减速直线运动,因此初速度 v0=16 m/s,末速度 v=0,加速度 a=-6 m/s 2 。
根据 v=v0 +at 得:
汽车 10 s 末的速度为 16 m/s,从刹车到停下来要用 2.67 s。
解题步骤:
1.认真审题,分析已知量和待求量;
2.弄清题意画示意图,明确初速度v0、末速度v、加速度a和时间t及各量的正负号。
3.将已知量带入公式求未知量,若所求量是矢量,要说明方向。
4.对计算结果和结论进行验算。
图中是一个物体运动的 v-t 图像。它的速度怎样变化?在相等的时间间隔内,即Δt ′ = Δt 时,速度的变化量Δv′和 Δv总是相等的吗?物体在做匀变速运动吗?
它的速度随着时间的增加逐渐增加;在相等的时间间隔内,即Δt ′ = Δt 时,速度的变化量Δv′小于Δv;物体在做加速度逐渐减小的加速运动
t1
t2
t3
t4
v
t
v2
v1
v3
v4
Δt
Δt ′
Δv′
Δv
思考:
1.某小汽车从静止开始,以a1=1.6m/s2的加速度沿直线匀加速行驶了t1=4s后,又以a2=1.2m/s2的加速度沿直线匀减速行驶了t2=3s,然后做匀速直线运动,则此小汽车做匀速直线运动的速度大小是( )
A.2.8m/s B.8m/s C.6.4m/s D.10m/s
A
2.在光滑足够长的斜面上,有一物体以10m/s的初速度沿斜面向上运动,如果物体的加速度大小始终为5m/s2,方向沿斜面向下,那么经过4s后物体的速度大小和方向是( )
A.30m/s,沿斜面向下 B.10m/s,沿斜面向下
C.20m/s,沿斜面向上 D.30m/s,沿斜面向上
B
3.甲、乙两物体在同一直线上做匀变速直线运动的速度-时间图像如图所示。由此可知( )
A.甲和乙的初速度方向相同,大小之比为3∶1
B.在t=4s时,两者的瞬时速度大小相等
C.甲和乙的加速度方向相同,大小之比为3∶1
D.甲和乙的加速度方向相反,大小之比为2∶1
A
4.如图所示是某质点运动的v-t图像,下列判断正确的是( )
A.在第2 s末,质点的速度方向发生改变
B.在0~2 s内,质点做直线运动,在2~4 s内,
质点做曲线运动
C.在0~2 s内,质点的加速度大小和方向均不变,质点做匀变速运动
D.在2~4 s内,质点的加速度不断减小,方向发生了改变
C
速度与时间的关系
公式: vt =v0+at
适用条件
特殊情况
第二章 匀变速直线运动
第2节 课时1 速度与时间的关系
1、这个v-t图像有什么特点?
0 1 2 3 4 5 6 7 8
0.2
0.4
0.6
0.8
1.0
v /m/s
t/s
2、表示的速度有什么特点?
3、表示的加速度又有什么特点?
1.是一条平行于时间轴的直线
2.表示速度不随时间变化,描述的是匀速直线运动
3.a = 0
1.理解匀变速直线运动的v-t图像特点。
2.理解匀变速直线运动的速度公式,并会用公式解决匀变速直线运动问题。
01 速度与时间的关系
1.数学推导
物体开始运动记为0时刻,初速度为v0,t 时刻速度为vt.
v = v 0 + at
v - v 0 = at
2.图像法
v
t
Δt
Δv
Δt
Δv
0 1 2 3 4 5 6 7 8 9
4 2
6
8
无论Δt选在什么区间,对应的速度的变化量Δv与时间的变化量Δt 之比都是一样的,即物体运动的加速度保持不变,称为匀变速直线运动。
匀变速直线运动 恒定不变(大小、方向均不变)
v
t
v0
Δv=at
vt
t
vt =v0+ v
vt = v 0 + at
3.类比一次函数 y=kx+b
匀变速直线运动 v - t图像是一条倾斜直线,
v 与t关系形如一次函数,v =kt+b
v-t 图像斜率为a,即k=a
截距为v0,即b = v0
∴ vt =v0+at
v
t
v0
vt
t
4.匀变速直线运动的速度与时间的关系式:
v t = v 0 + at
at 是 t 时间内速度的变化量,再加上物体在开始时刻的速度v0, 就是t时刻的速度vt。
vt
t
v
t
o
v0
t
Δv=at
(1)此关系式只适用于匀变速直线运动
(3)此关系式为矢量式,注意方向(若取初速方向为正,则加速运动 a 为正,减速运动 a 为负)
(1)当 v 0= 0 时,v t = at
物体做初速度为零的匀加速直线运动
(2)当 a = 0 时, v t = v0
物体做匀速直线运动
5. v t= v 0 + at的特殊形式
讨论与交流1:如图所示是三个质点的v-t图像,图线①②③表示的运动情况是怎样的?图像中图线的交点表示什么含义?
①匀加速直线运动
②匀速直线运动
③匀减速直线运动
当两图线有交点时,
表示两物体在此时刻速度相等。
讨论与交流2:如图所示是某质点运动的v-t图像。试描述该图像与物体运动实际情况的对应关系。请求出该物体每个时间段的加速度。
①在0~1s内,物体做初速度为零的匀加速直线运动至1s末速度为4m/s
③在3~4s内,物体做匀减速直线运动至4s末速度为零
②在1~3s内,物体做匀变速直线运动至3s末速度为-4m/s (在1~2s内,物体做匀减速直线运动至2s末速度为零,2~3s内,物体做反向匀加速直线运动至3s末速度为-4m/s)
①
②
③
例题:一辆汽车以 36 km/h 的速度在平直公路上匀速行驶。从某时刻起,它以 0.6 m/s2的加速度加速,10s 末因故突然紧急刹车,随后汽车停了下来。刹车时做匀减速运动的加速度大小是 6 m/s2 。
(1)汽车在 10 s 末的速度是多少?
(2)汽车从刹车到停下来用了多长时间?
分析:依题意,汽车加速和减速过程都是在做匀变速直线运动。第(1)问是已知加速的时间求末速度。
第(2)问是已知末速度求减速的时间。两个问题都需要用匀变速直线运动的速度与时间关系式来求解。其中,第(2)问汽车加速度的方向跟速度、位移的方向相反,需要建立坐标系处理物理量之间的正负号问题。
解:(1)汽车做匀加速直线运动。
初速度 v0=36 km/h =10 m/s,加速度 a=0.6 m/s2 ,时间 t=10 s根据匀变速直线运动速度与时间的关系式,有
v=v0+at =10 m/s+0.6 m/s2 ×10 s=16 m/s
(2)以汽车运动方向为正方向建立一维坐标系(如图 ),与正方向一致的量取正号,相反的取负号。
v
a
0
x
汽车从第 10 s 末开始做匀减速直线运动,因此初速度 v0=16 m/s,末速度 v=0,加速度 a=-6 m/s 2 。
根据 v=v0 +at 得:
汽车 10 s 末的速度为 16 m/s,从刹车到停下来要用 2.67 s。
解题步骤:
1.认真审题,分析已知量和待求量;
2.弄清题意画示意图,明确初速度v0、末速度v、加速度a和时间t及各量的正负号。
3.将已知量带入公式求未知量,若所求量是矢量,要说明方向。
4.对计算结果和结论进行验算。
图中是一个物体运动的 v-t 图像。它的速度怎样变化?在相等的时间间隔内,即Δt ′ = Δt 时,速度的变化量Δv′和 Δv总是相等的吗?物体在做匀变速运动吗?
它的速度随着时间的增加逐渐增加;在相等的时间间隔内,即Δt ′ = Δt 时,速度的变化量Δv′小于Δv;物体在做加速度逐渐减小的加速运动
t1
t2
t3
t4
v
t
v2
v1
v3
v4
Δt
Δt ′
Δv′
Δv
思考:
1.某小汽车从静止开始,以a1=1.6m/s2的加速度沿直线匀加速行驶了t1=4s后,又以a2=1.2m/s2的加速度沿直线匀减速行驶了t2=3s,然后做匀速直线运动,则此小汽车做匀速直线运动的速度大小是( )
A.2.8m/s B.8m/s C.6.4m/s D.10m/s
A
2.在光滑足够长的斜面上,有一物体以10m/s的初速度沿斜面向上运动,如果物体的加速度大小始终为5m/s2,方向沿斜面向下,那么经过4s后物体的速度大小和方向是( )
A.30m/s,沿斜面向下 B.10m/s,沿斜面向下
C.20m/s,沿斜面向上 D.30m/s,沿斜面向上
B
3.甲、乙两物体在同一直线上做匀变速直线运动的速度-时间图像如图所示。由此可知( )
A.甲和乙的初速度方向相同,大小之比为3∶1
B.在t=4s时,两者的瞬时速度大小相等
C.甲和乙的加速度方向相同,大小之比为3∶1
D.甲和乙的加速度方向相反,大小之比为2∶1
A
4.如图所示是某质点运动的v-t图像,下列判断正确的是( )
A.在第2 s末,质点的速度方向发生改变
B.在0~2 s内,质点做直线运动,在2~4 s内,
质点做曲线运动
C.在0~2 s内,质点的加速度大小和方向均不变,质点做匀变速运动
D.在2~4 s内,质点的加速度不断减小,方向发生了改变
C
速度与时间的关系
公式: vt =v0+at
适用条件
特殊情况
同课章节目录
- 第一章 运动的描述
- 第一节 质点 参考系 时间
- 第二节 位置 位移
- 第三节 速度
- 第四节 测量直线运动物体的瞬时速度
- 第五节 加速度
- 第二章 匀变速直线运动
- 第一节 匀变速直线运动的特点
- 第二节 匀变速直线运动的规律
- 第三节 测量匀变速直线运动的加速度
- 第四节 自由落体运动
- 第五节 匀变速直线运动与汽车安全行驶
- 第三章 相互作用
- 第一节 重力
- 第二节 弹力
- 第三节 摩擦力
- 第四节 力的合成
- 第五节 力的分解
- 第六节 共点力的平衡条件及其应用
- 第四章 牛顿运动定律
- 第一节 牛顿第一定律
- 第二节 加速度与力、质量之间的关系
- 第三节 牛顿第二定律
- 第四节 牛顿第三定律
- 第五节 牛顿运动定律的应用
- 第六节 失重和超重
- 第七节 力学单位
