2.2 课时2 位移与时间、速度与时间的关系(24张PPT)课件 2024-2025学年高一物理粤教版(2019)必修第一册
文档属性
| 名称 | 2.2 课时2 位移与时间、速度与时间的关系(24张PPT)课件 2024-2025学年高一物理粤教版(2019)必修第一册 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 粤教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-08-08 14:19:33 | ||
图片预览




文档简介
(共24张PPT)
第二章 匀变速直线运动
第2节 课时2 位移与时间、速度与时间的关系
结论:匀速直线运动的v – t 图象与t轴所围的矩形“面积”就等于“位移”。
v
(m·s-1)
/
t
s
/
v0
o
t
匀变速直线运动的位移是否也可以用v-t图象与t轴所围的“面积”表示呢?
1.知道匀速直线运动的位移与v-t图像中图线与坐标轴所围面积的对应关系。
2.理解匀变速直线运动的位移公式的推导方法,感受利用极限思想解决物理问题的科学思维方法。
3.理解匀变速直线运动的位移公式、速度与位移的关系式,会应用公式分析匀变速直线运动问题。
01 匀变速直线运动的位移
1
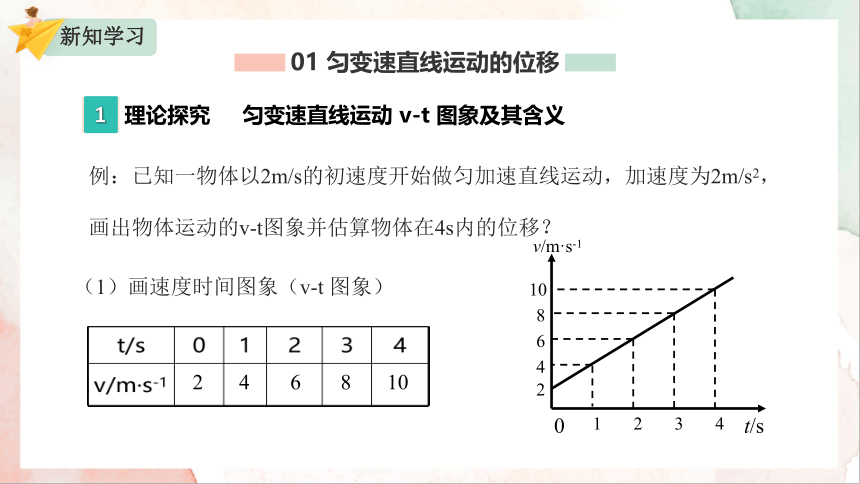
理论探究 匀变速直线运动 v-t 图象及其含义
例:已知一物体以2m/s的初速度开始做匀加速直线运动,加速度为2m/s2,画出物体运动的v-t图象并估算物体在4s内的位移?
t/s
4
3
2
1
0
2
4
6
10
8
v/m·s-1
(1)画速度时间图象(v-t 图象)
2
4
6
8
10
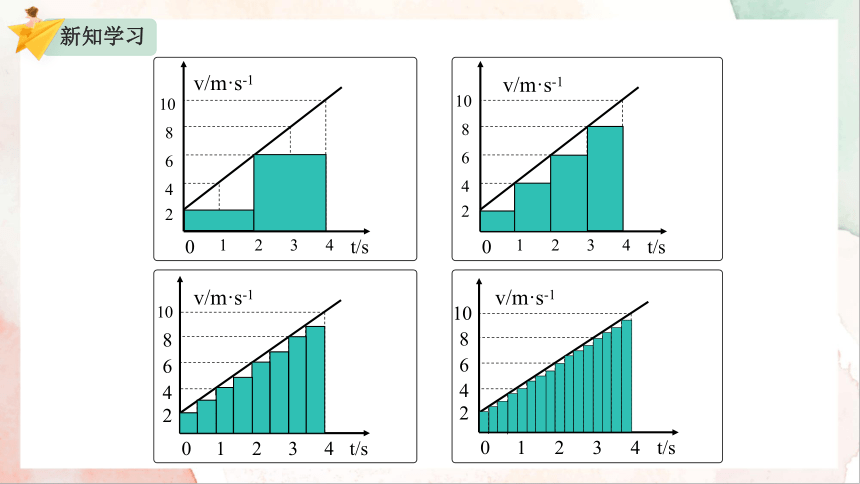
将“匀变速”转化为“匀速”
分 段
科学思想方法:先把过程无限分割(微分),逐渐逼近,以“不变”近似代替“变”;然后再进行累加(积分),逐渐吻合的思想 。
t/s
4
3
2
1
0
2
4
6
10
8
v/m·s-1
t/s
4
3
2
1
0
2
4
6
10
8
v/m·s-1
t/s
4
3
2
1
0
2
4
6
10
8
v/m·s-1
t/s
4
3
2
1
0
2
4
6
10
8
v/m·s-1
t/s
4
3
2
1
0
2
4
6
10
8
v/m·s-1
t/s
4
3
2
1
0
2
4
6
10
8
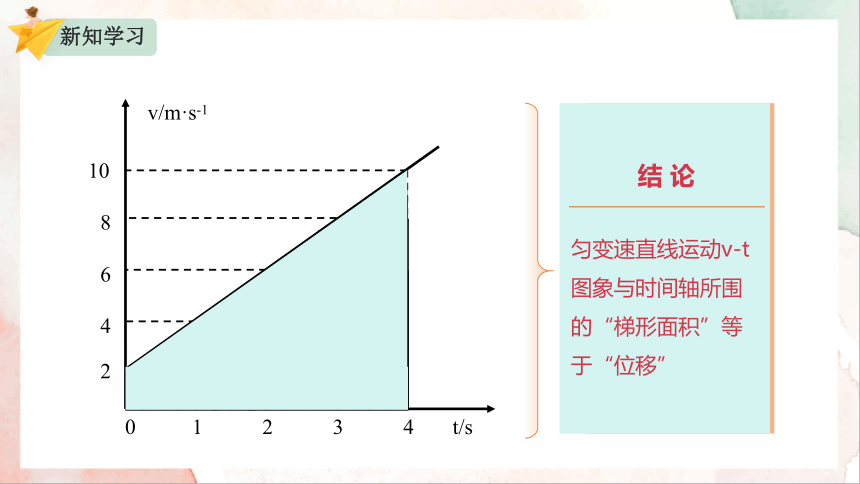
结 论
匀变速直线运动v-t 图象与时间轴所围的“梯形面积”等于“位移”
v/m·s-1
2
推导匀变速直线运动的位移公式
由图可知:梯形OABC的面积
S=(OC+AB)×OA/2
代入各物理量得:
又v=v0+at
v
v0
v
B
A
o
t
t
C
得:
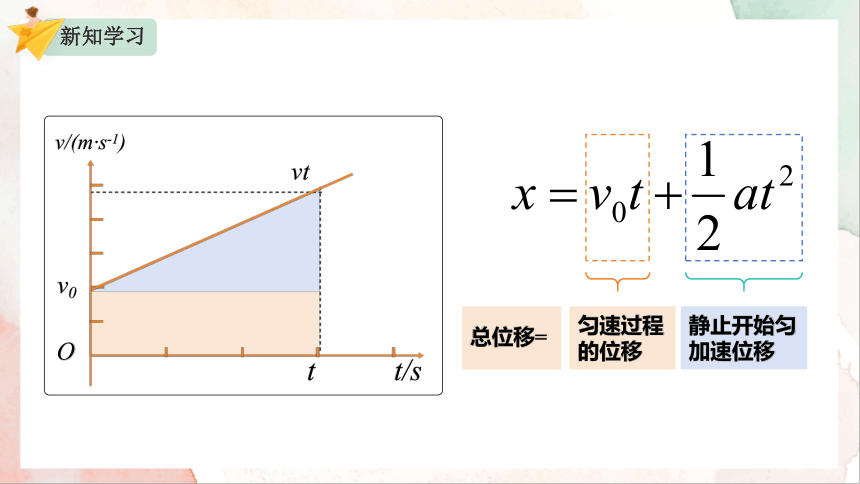
匀变速直线运动位移与
时间的关系式(简称位移公式)
v/(m·s-1)
O
t
t/s
v0
vt
总位移=
匀速过程的位移
静止开始匀加速位移
(5)公式中4个物理量(不涉及末速度),知任三求剩一;代入数据时,各物理量的单位要统一 (一般用国际制单位) 。
(1)反映了匀变速直线运动的位移与时间是二次函数关系,x-t图象是一元二次函数曲线(抛物线)。
(2)公式适用于匀变速(包括匀加速或匀减速)直线运动。
(3)是矢量式,使用公式时应先规定正方向。(一般取v0的方向为正方向)若物体做匀加速运动,a取正值;若物体做匀减速运动,则a取负值。
(4) 若位移的计算结果为正值,说明位移方向与规定的正方向相同;若位移的计算结果为负值,说明位移方向与规定的正方向相反。
3
对位移公式的理解
① 当v0=0时,x= ,即由静止开始的匀加速直线运动,位移x与t2成正比。
② 当a=0时,x=v0t,即匀速直线运动的位移公式。
注 意
逆向思维法:末速度为 0 的匀减速直线运动可视为反方向的初速度为 0 的匀加速直线运动。
4
位移与时间关系的两种特殊形式
A、B表示物体做匀速直线运动,C表示物体处于静止状态,D 表示物体做什么运动呢(是一条抛物线)?
提示:当v0=0,由x= 。
知其x-t图是一条过原点的抛物线,如图D所示。
认识匀变速直线运动的x-t图
【例题】航空母舰的舰载机既要在航母上起飞,也要在航母上降落。
(1)某舰载机起飞时,采用弹射装置使飞机获得 10 m/s 的速度后,由机上发动机使飞机获得 25 m/s2 的加速度在航母跑道上匀加速前进,2.4 s 后离舰升空。飞机匀加速滑行的距离是多少?
(2)飞机在航母上降落时,需用阻拦索使飞机迅
速停下来。若某次飞机着舰时的速度为 80 m/s,
飞机钩住阻拦索后经过 2.5 s停下来。将这段运
动视为匀减速直线运动,此过程中飞机加速度的
大小及滑行的距离各是多少?
【分析 】两个问题都是已知匀变速直线运动的时间来计算位移。
第(1)问需要用匀变速直线运动的位移与时间的关系式计算。
第(2)问中,飞机着舰做匀减速直线运动的加速度需要根据速度与时间的关系式计算。匀减速运动各矢量的方向较为复杂,因此需要建立一维坐标系来确定它们的正负。
【解析】(1)根据匀变速直线运动的位移与时间的关系式,有
(2)沿飞机滑行方向建立一维坐标系,飞机初速度v0=80 m/s,
末速度v=0,根据匀变速直线运动的速度与时间的关系式,有
加速度为负值表示方向与 x 轴正方向相反。再根据匀变速直线
运动的位移与时间的关系式,有
a不变
位移
v=v0+at
?
时间
位移
速度
速度时间关系
位移时间关系
速度位移关系
【问题】在某城市的一条道路上,规定车辆行驶速度不得超过30km/h,在一次交通事故中,肇事车是一辆客车,量得这辆车紧急刹车时留下的刹车痕迹长为7.6m,已知该客车刹车时的加速度大小为7m/s2。请判断该车是否超速。
【解析】以客车开始刹车时的位置为原点,沿客车行驶方向建立坐标轴,则
x=7.6m
v0
a=-7m/s2
v=0
v2 – v02 = 2ax
①
②
由①式有
③
将③式代入②式,有
可 得
(2)若 v0=0,
说 明
(1)只适用于匀变速直线运动;
1.速度与位移公式的推导
02 速度与位移的关系
2.速度与位移图像
v2-x 图像
斜率:k=2a
x-v2 图像
斜率:k=1/2a
1.100m决赛中,某运动员的起跑反应时间是0.170s,加速过程可以看成匀加速直线运动,加速时间约为2.5s,最大速度约为12m/s,则该运动员在加速阶段的加速度与位移约为( )
A.4.8m/s2 16m B.4.8m/s2 15m
C.4.5m/s2 16m D.4.5m/s2 15m
B
A.甲的初速度为36m/s
B.甲的加速度为2m/s2
C.两车在6m处相遇
D.甲停止前,两车在2s时相距最远
2.甲、乙两辆汽车同时同地出发,沿同方向做直线运动,两车速度的平方 v2 随位移 x 的变化图象如图所示,下列说法正确的是( )
D
3.动车铁轨旁两相邻里程碑之间的距离是1km。某同学乘坐动车时,通过观察里程碑和车厢内电子屏上显示的动车速度来估算动车减速进站时的加速度大小。当他身边的窗户经过某一里程碑时,
屏幕显示的动车速度是126km/h。动车又前
进了 3 个里程碑时,速度变为54 km/h。把
动车进站过程视为匀减速直线运动。那么动
车进站的加速度是多少?它还要行驶多远才
能停下来?
【解析】 沿动车运动方向为正方向建立一维坐标系。把动车通过 3 000 m 的运动称为前一过程,之后到停下来称为后一过程。
设在前一过程中的末位置为 M 点。 初速度 v0 =126km/h=35m/s,
末速度 vM=54 km/h=15 m/s,位移x1=3000m。
对前一过程,根据匀变速直线运动的速度与位移的关系式,有
对后一过程,末速度 v = 0,初速度 vM = 15 m/s由
v2 = vM2 + 2ax2,有
a=
x2=
五个量知道
了三个量,
就能求出其
余两个量。
不涉及时间
不涉及位移
不涉及末速度
第二章 匀变速直线运动
第2节 课时2 位移与时间、速度与时间的关系
结论:匀速直线运动的v – t 图象与t轴所围的矩形“面积”就等于“位移”。
v
(m·s-1)
/
t
s
/
v0
o
t
匀变速直线运动的位移是否也可以用v-t图象与t轴所围的“面积”表示呢?
1.知道匀速直线运动的位移与v-t图像中图线与坐标轴所围面积的对应关系。
2.理解匀变速直线运动的位移公式的推导方法,感受利用极限思想解决物理问题的科学思维方法。
3.理解匀变速直线运动的位移公式、速度与位移的关系式,会应用公式分析匀变速直线运动问题。
01 匀变速直线运动的位移
1
理论探究 匀变速直线运动 v-t 图象及其含义
例:已知一物体以2m/s的初速度开始做匀加速直线运动,加速度为2m/s2,画出物体运动的v-t图象并估算物体在4s内的位移?
t/s
4
3
2
1
0
2
4
6
10
8
v/m·s-1
(1)画速度时间图象(v-t 图象)
2
4
6
8
10
将“匀变速”转化为“匀速”
分 段
科学思想方法:先把过程无限分割(微分),逐渐逼近,以“不变”近似代替“变”;然后再进行累加(积分),逐渐吻合的思想 。
t/s
4
3
2
1
0
2
4
6
10
8
v/m·s-1
t/s
4
3
2
1
0
2
4
6
10
8
v/m·s-1
t/s
4
3
2
1
0
2
4
6
10
8
v/m·s-1
t/s
4
3
2
1
0
2
4
6
10
8
v/m·s-1
t/s
4
3
2
1
0
2
4
6
10
8
v/m·s-1
t/s
4
3
2
1
0
2
4
6
10
8
结 论
匀变速直线运动v-t 图象与时间轴所围的“梯形面积”等于“位移”
v/m·s-1
2
推导匀变速直线运动的位移公式
由图可知:梯形OABC的面积
S=(OC+AB)×OA/2
代入各物理量得:
又v=v0+at
v
v0
v
B
A
o
t
t
C
得:
匀变速直线运动位移与
时间的关系式(简称位移公式)
v/(m·s-1)
O
t
t/s
v0
vt
总位移=
匀速过程的位移
静止开始匀加速位移
(5)公式中4个物理量(不涉及末速度),知任三求剩一;代入数据时,各物理量的单位要统一 (一般用国际制单位) 。
(1)反映了匀变速直线运动的位移与时间是二次函数关系,x-t图象是一元二次函数曲线(抛物线)。
(2)公式适用于匀变速(包括匀加速或匀减速)直线运动。
(3)是矢量式,使用公式时应先规定正方向。(一般取v0的方向为正方向)若物体做匀加速运动,a取正值;若物体做匀减速运动,则a取负值。
(4) 若位移的计算结果为正值,说明位移方向与规定的正方向相同;若位移的计算结果为负值,说明位移方向与规定的正方向相反。
3
对位移公式的理解
① 当v0=0时,x= ,即由静止开始的匀加速直线运动,位移x与t2成正比。
② 当a=0时,x=v0t,即匀速直线运动的位移公式。
注 意
逆向思维法:末速度为 0 的匀减速直线运动可视为反方向的初速度为 0 的匀加速直线运动。
4
位移与时间关系的两种特殊形式
A、B表示物体做匀速直线运动,C表示物体处于静止状态,D 表示物体做什么运动呢(是一条抛物线)?
提示:当v0=0,由x= 。
知其x-t图是一条过原点的抛物线,如图D所示。
认识匀变速直线运动的x-t图
【例题】航空母舰的舰载机既要在航母上起飞,也要在航母上降落。
(1)某舰载机起飞时,采用弹射装置使飞机获得 10 m/s 的速度后,由机上发动机使飞机获得 25 m/s2 的加速度在航母跑道上匀加速前进,2.4 s 后离舰升空。飞机匀加速滑行的距离是多少?
(2)飞机在航母上降落时,需用阻拦索使飞机迅
速停下来。若某次飞机着舰时的速度为 80 m/s,
飞机钩住阻拦索后经过 2.5 s停下来。将这段运
动视为匀减速直线运动,此过程中飞机加速度的
大小及滑行的距离各是多少?
【分析 】两个问题都是已知匀变速直线运动的时间来计算位移。
第(1)问需要用匀变速直线运动的位移与时间的关系式计算。
第(2)问中,飞机着舰做匀减速直线运动的加速度需要根据速度与时间的关系式计算。匀减速运动各矢量的方向较为复杂,因此需要建立一维坐标系来确定它们的正负。
【解析】(1)根据匀变速直线运动的位移与时间的关系式,有
(2)沿飞机滑行方向建立一维坐标系,飞机初速度v0=80 m/s,
末速度v=0,根据匀变速直线运动的速度与时间的关系式,有
加速度为负值表示方向与 x 轴正方向相反。再根据匀变速直线
运动的位移与时间的关系式,有
a不变
位移
v=v0+at
?
时间
位移
速度
速度时间关系
位移时间关系
速度位移关系
【问题】在某城市的一条道路上,规定车辆行驶速度不得超过30km/h,在一次交通事故中,肇事车是一辆客车,量得这辆车紧急刹车时留下的刹车痕迹长为7.6m,已知该客车刹车时的加速度大小为7m/s2。请判断该车是否超速。
【解析】以客车开始刹车时的位置为原点,沿客车行驶方向建立坐标轴,则
x=7.6m
v0
a=-7m/s2
v=0
v2 – v02 = 2ax
①
②
由①式有
③
将③式代入②式,有
可 得
(2)若 v0=0,
说 明
(1)只适用于匀变速直线运动;
1.速度与位移公式的推导
02 速度与位移的关系
2.速度与位移图像
v2-x 图像
斜率:k=2a
x-v2 图像
斜率:k=1/2a
1.100m决赛中,某运动员的起跑反应时间是0.170s,加速过程可以看成匀加速直线运动,加速时间约为2.5s,最大速度约为12m/s,则该运动员在加速阶段的加速度与位移约为( )
A.4.8m/s2 16m B.4.8m/s2 15m
C.4.5m/s2 16m D.4.5m/s2 15m
B
A.甲的初速度为36m/s
B.甲的加速度为2m/s2
C.两车在6m处相遇
D.甲停止前,两车在2s时相距最远
2.甲、乙两辆汽车同时同地出发,沿同方向做直线运动,两车速度的平方 v2 随位移 x 的变化图象如图所示,下列说法正确的是( )
D
3.动车铁轨旁两相邻里程碑之间的距离是1km。某同学乘坐动车时,通过观察里程碑和车厢内电子屏上显示的动车速度来估算动车减速进站时的加速度大小。当他身边的窗户经过某一里程碑时,
屏幕显示的动车速度是126km/h。动车又前
进了 3 个里程碑时,速度变为54 km/h。把
动车进站过程视为匀减速直线运动。那么动
车进站的加速度是多少?它还要行驶多远才
能停下来?
【解析】 沿动车运动方向为正方向建立一维坐标系。把动车通过 3 000 m 的运动称为前一过程,之后到停下来称为后一过程。
设在前一过程中的末位置为 M 点。 初速度 v0 =126km/h=35m/s,
末速度 vM=54 km/h=15 m/s,位移x1=3000m。
对前一过程,根据匀变速直线运动的速度与位移的关系式,有
对后一过程,末速度 v = 0,初速度 vM = 15 m/s由
v2 = vM2 + 2ax2,有
a=
x2=
五个量知道
了三个量,
就能求出其
余两个量。
不涉及时间
不涉及位移
不涉及末速度
同课章节目录
- 第一章 运动的描述
- 第一节 质点 参考系 时间
- 第二节 位置 位移
- 第三节 速度
- 第四节 测量直线运动物体的瞬时速度
- 第五节 加速度
- 第二章 匀变速直线运动
- 第一节 匀变速直线运动的特点
- 第二节 匀变速直线运动的规律
- 第三节 测量匀变速直线运动的加速度
- 第四节 自由落体运动
- 第五节 匀变速直线运动与汽车安全行驶
- 第三章 相互作用
- 第一节 重力
- 第二节 弹力
- 第三节 摩擦力
- 第四节 力的合成
- 第五节 力的分解
- 第六节 共点力的平衡条件及其应用
- 第四章 牛顿运动定律
- 第一节 牛顿第一定律
- 第二节 加速度与力、质量之间的关系
- 第三节 牛顿第二定律
- 第四节 牛顿第三定律
- 第五节 牛顿运动定律的应用
- 第六节 失重和超重
- 第七节 力学单位
