2.3 课时1 匀变速直线运动的位移与时间关系(22张PPT)课件 2024-2025学年高一物理人教版(2019)必修第一册
文档属性
| 名称 | 2.3 课时1 匀变速直线运动的位移与时间关系(22张PPT)课件 2024-2025学年高一物理人教版(2019)必修第一册 |  | |
| 格式 | pptx | ||
| 文件大小 | 623.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-08-08 14:33:00 | ||
图片预览






文档简介
(共22张PPT)
第二章 匀变速直线运动的研究
第3节 课时2 匀变速直线运动的推论
匀速直线运动的位移与时间的的关系:
x=vt,它的v-t图象是平行于t轴的一条直线。
0
v/(m s-1)
t/s
t
v
如图v – t 图线与t轴所夹的矩形“面积”就是匀速直线运动的位移。
x=vt
做匀变速直线运动的物体,在时间t内的位移与时间会有怎样的关系?
1.知道匀变速直线运动v-t图像的特点,理解图像的物理意义。
2.掌握匀变速直线运动的速度与时间关系式,并能利用所学公式分析解决相关问题。
知识点一:匀变速速直线运动的位移
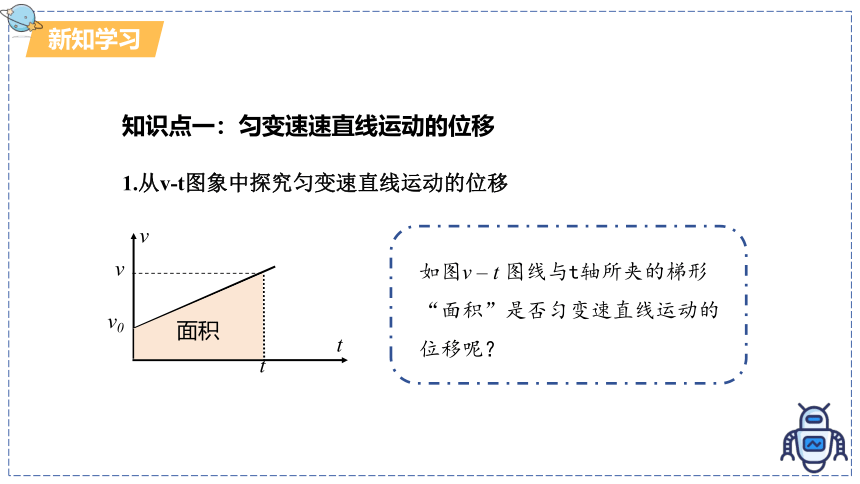
1.从v-t图象中探究匀变速直线运动的位移
v
t
v0
v
t
面积
如图v – t 图线与t轴所夹的梯形“面积”是否匀变速直线运动的位移呢?
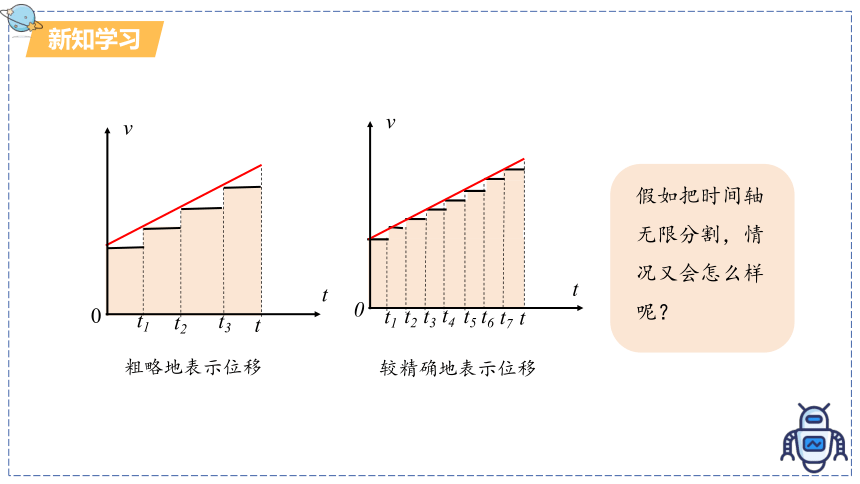
粗略地表示位移
较精确地表示位移
v
t
0
t
t1
t2
t3
v
t
0
t
t1
t2
t3
t4
t5
t6
t7
假如把时间轴无限分割,情况又会怎么样呢?
v0
v
0
t
t
如果把整个运动过程分割得非常非常细,很多很多小矩形的面积之和就能非常精确地代表物体的位移了。这是物理上常用的微元法。
匀变速直线运动的位移仍可用图线与坐标轴所围的面积表示。
v
下面请同学们依据这个结论和v-t图象,求得位移的计算式。
v0
0
t/s
t
由图可知梯形的面积:S梯形=
v
v
即位移:
将 v = v 0 + at 代入上式,有
v/(m s-1)
2.匀变速速直线运动的位移公式:
(1)t是指物体运动的实际时间(刹车问题)
(2)使用公式时应先规定正方向,一般以v0的方向为正方向,若a与v0同向,则a取正值;若a与v0反向,则a取负值;
(3)如果初速度为 0,
(4)解题时先用字母代表物理量,再代入数值进行计算,代入数据时,各物理量的单位要统一。
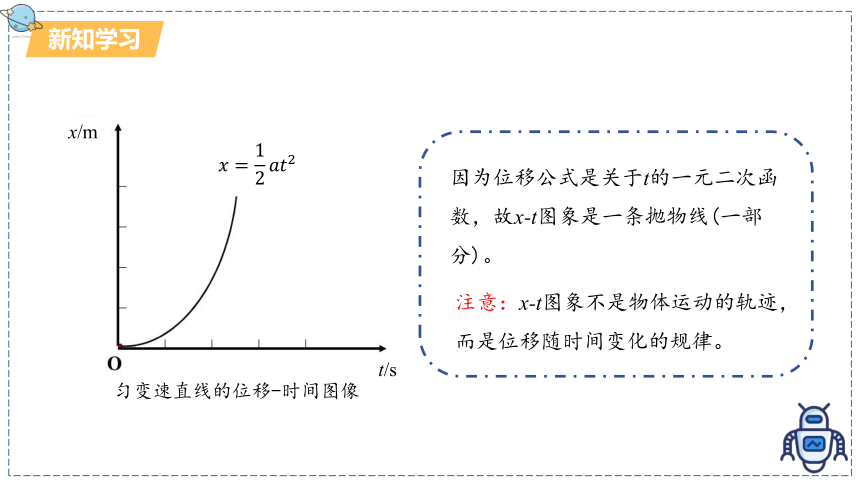
匀变速直线的位移-时间图像
因为位移公式是关于t的一元二次函数,故x-t图象是一条抛物线(一部分)。
注意:x-t图象不是物体运动的轨迹,而是位移随时间变化的规律。
x/m
t/s
【例题】航空母舰的舰载机既要在航母上起飞,也要在航母上降落。
(1)某舰载机起飞时,采用弹射装置使飞机获得10 m/s的速度后,由机上发动机使飞机获得25 m/s2 的加速度在航母跑道上匀加速前进,2.4 s后离舰升空。飞机匀加速滑行的距离是多少?
(2)飞机在航母上降落时,需用阻拦索使飞机迅速停下来。若某次飞机着舰时的速度为80 m/s,飞机钩住阻拦索后经过2.5 s 停下来。将这段运动视为匀减速直线运动,此过程中飞机加速度的大小及滑行的距离各是多少?
分析:两个问题都是已知匀变速直线运动的时间来计算位移。
第(1)问需要用匀变速直线运动的位移与时间的关系式计算。
第(2)问中,飞机着舰做匀减速直线运动的加速度需要根据速度与时间的关系式计算。匀减速运动各矢量的方向较为复杂,因此需要建立一维坐标系来确定它们的正负。
解 (1)根据匀变速直线运动的位移与时间的关系式,有
= 10 m/s×2.4 s +1/2×25 m/s 2 ×(2.4 s)2= 96 m
(2)沿飞机滑行方向建立一维坐标系如图所示,飞机初速度v0=80 m/s,
末速度v=0,根据匀变速直线运动的速度与时间的关系式,有
v0
O
x
加速度为负值表示方向与x轴正方向相反。
再根据匀变速直线运动的位移与时间的关系式,有
= v0t + ×(- )t2
= v0t = ×80 m/s×2.5 s = 100 m
飞机起飞时滑行距离为96 m。着舰过程中加速度的大小为32 m/s2 ,滑行距离为100 m。
射击时,燃气膨胀推动弹头加速运动。若把子弹在枪筒中的运动看做匀加速直线运动,设子弹的加速度a=5×105m/s2,枪筒长x=0.64m,求子弹射出枪口时的速度。
t=1.6×10-3s
v=at=800m/s
知识点三:匀变速直线运动速度与位移的关系
解:以子弹射出枪口时速度 v 方向为正方向
由位移公式:
又由速度公式: v=v0+at
在此问题中,时间 t 只是一个中间量,因此要分步解决,能不能用一个不含时间的公式直接解决呢?
可得:
v==800m/s
公式变形
注意:
1.该公式只适用匀变速直线运动
2.该公式是矢量式
因为v0、v、α、x均为矢量,使用公式时应先规定正方向。
(一般以v0的方向为正方向)
若物体做匀加速运动,a取正值,
若物体做匀减速运动,则a取负值.
1.一物体以2 m/s的初速度做匀加速直线运动,4 s内的位移为16 m,则 ( )
A.物体的加速度大小为2 m/s2
B.物体在4 s内的平均速度大小为6 m/s
C.物体在4 s末的瞬时速度大小为6 m/s
D.物体在第2 s内的位移大小为6 m
C
2.飞机的起飞过程是飞机在直跑道上由静止开始加速前进,达到一定速度时离地。已知飞机加速前进的路程为1600 m,所用的时间为40 s。假设这段时间内飞机的运动为匀加速运动,用a表示加速度,用v表示离地时的速度,则 ( )
A.a=2 m/s2,v=80 m/s
B.a=1 m/s2,v=40 m/s
C.a=2 m/s2,v=40 m/s
D.a=1 m/s2,v=80 m/s
A
3.(多选)由静止开始做匀加速直线运动的火车,在第10 s末的速度为2 m/s,下列叙述中正确的是( )
A.前10 s内,火车通过的位移为10 m
B.火车每秒速度变化0.2 m/s
C.前10 s内,火车的平均速度为1 m/s
D.第10 s内,火车通过的位移为2 m
ABC
4.一空间探测器从某一星球表面竖直升空,其速度随时间的变化情况如图所示,图线上A、B、C三点对应的时刻分别为9 s、25 s和45 s,下列说法正确的是 ( )
A.上升和下落两个过程中,探测器的加速度之比为9∶16
B.探测器9 s后开始下落
C.探测器上升的最大高度为288 m
D.图中BC过程中探测器的平均速度大小为40 m/s
D
匀变速直线运动的位移与时间的关系
v-t图象所围面积的意义
位移——时间公式x=v0t+ at2的推导和应用
速度——位移公式v2–v02 =2ax的推导和应用
第二章 匀变速直线运动的研究
第3节 课时2 匀变速直线运动的推论
匀速直线运动的位移与时间的的关系:
x=vt,它的v-t图象是平行于t轴的一条直线。
0
v/(m s-1)
t/s
t
v
如图v – t 图线与t轴所夹的矩形“面积”就是匀速直线运动的位移。
x=vt
做匀变速直线运动的物体,在时间t内的位移与时间会有怎样的关系?
1.知道匀变速直线运动v-t图像的特点,理解图像的物理意义。
2.掌握匀变速直线运动的速度与时间关系式,并能利用所学公式分析解决相关问题。
知识点一:匀变速速直线运动的位移
1.从v-t图象中探究匀变速直线运动的位移
v
t
v0
v
t
面积
如图v – t 图线与t轴所夹的梯形“面积”是否匀变速直线运动的位移呢?
粗略地表示位移
较精确地表示位移
v
t
0
t
t1
t2
t3
v
t
0
t
t1
t2
t3
t4
t5
t6
t7
假如把时间轴无限分割,情况又会怎么样呢?
v0
v
0
t
t
如果把整个运动过程分割得非常非常细,很多很多小矩形的面积之和就能非常精确地代表物体的位移了。这是物理上常用的微元法。
匀变速直线运动的位移仍可用图线与坐标轴所围的面积表示。
v
下面请同学们依据这个结论和v-t图象,求得位移的计算式。
v0
0
t/s
t
由图可知梯形的面积:S梯形=
v
v
即位移:
将 v = v 0 + at 代入上式,有
v/(m s-1)
2.匀变速速直线运动的位移公式:
(1)t是指物体运动的实际时间(刹车问题)
(2)使用公式时应先规定正方向,一般以v0的方向为正方向,若a与v0同向,则a取正值;若a与v0反向,则a取负值;
(3)如果初速度为 0,
(4)解题时先用字母代表物理量,再代入数值进行计算,代入数据时,各物理量的单位要统一。
匀变速直线的位移-时间图像
因为位移公式是关于t的一元二次函数,故x-t图象是一条抛物线(一部分)。
注意:x-t图象不是物体运动的轨迹,而是位移随时间变化的规律。
x/m
t/s
【例题】航空母舰的舰载机既要在航母上起飞,也要在航母上降落。
(1)某舰载机起飞时,采用弹射装置使飞机获得10 m/s的速度后,由机上发动机使飞机获得25 m/s2 的加速度在航母跑道上匀加速前进,2.4 s后离舰升空。飞机匀加速滑行的距离是多少?
(2)飞机在航母上降落时,需用阻拦索使飞机迅速停下来。若某次飞机着舰时的速度为80 m/s,飞机钩住阻拦索后经过2.5 s 停下来。将这段运动视为匀减速直线运动,此过程中飞机加速度的大小及滑行的距离各是多少?
分析:两个问题都是已知匀变速直线运动的时间来计算位移。
第(1)问需要用匀变速直线运动的位移与时间的关系式计算。
第(2)问中,飞机着舰做匀减速直线运动的加速度需要根据速度与时间的关系式计算。匀减速运动各矢量的方向较为复杂,因此需要建立一维坐标系来确定它们的正负。
解 (1)根据匀变速直线运动的位移与时间的关系式,有
= 10 m/s×2.4 s +1/2×25 m/s 2 ×(2.4 s)2= 96 m
(2)沿飞机滑行方向建立一维坐标系如图所示,飞机初速度v0=80 m/s,
末速度v=0,根据匀变速直线运动的速度与时间的关系式,有
v0
O
x
加速度为负值表示方向与x轴正方向相反。
再根据匀变速直线运动的位移与时间的关系式,有
= v0t + ×(- )t2
= v0t = ×80 m/s×2.5 s = 100 m
飞机起飞时滑行距离为96 m。着舰过程中加速度的大小为32 m/s2 ,滑行距离为100 m。
射击时,燃气膨胀推动弹头加速运动。若把子弹在枪筒中的运动看做匀加速直线运动,设子弹的加速度a=5×105m/s2,枪筒长x=0.64m,求子弹射出枪口时的速度。
t=1.6×10-3s
v=at=800m/s
知识点三:匀变速直线运动速度与位移的关系
解:以子弹射出枪口时速度 v 方向为正方向
由位移公式:
又由速度公式: v=v0+at
在此问题中,时间 t 只是一个中间量,因此要分步解决,能不能用一个不含时间的公式直接解决呢?
可得:
v==800m/s
公式变形
注意:
1.该公式只适用匀变速直线运动
2.该公式是矢量式
因为v0、v、α、x均为矢量,使用公式时应先规定正方向。
(一般以v0的方向为正方向)
若物体做匀加速运动,a取正值,
若物体做匀减速运动,则a取负值.
1.一物体以2 m/s的初速度做匀加速直线运动,4 s内的位移为16 m,则 ( )
A.物体的加速度大小为2 m/s2
B.物体在4 s内的平均速度大小为6 m/s
C.物体在4 s末的瞬时速度大小为6 m/s
D.物体在第2 s内的位移大小为6 m
C
2.飞机的起飞过程是飞机在直跑道上由静止开始加速前进,达到一定速度时离地。已知飞机加速前进的路程为1600 m,所用的时间为40 s。假设这段时间内飞机的运动为匀加速运动,用a表示加速度,用v表示离地时的速度,则 ( )
A.a=2 m/s2,v=80 m/s
B.a=1 m/s2,v=40 m/s
C.a=2 m/s2,v=40 m/s
D.a=1 m/s2,v=80 m/s
A
3.(多选)由静止开始做匀加速直线运动的火车,在第10 s末的速度为2 m/s,下列叙述中正确的是( )
A.前10 s内,火车通过的位移为10 m
B.火车每秒速度变化0.2 m/s
C.前10 s内,火车的平均速度为1 m/s
D.第10 s内,火车通过的位移为2 m
ABC
4.一空间探测器从某一星球表面竖直升空,其速度随时间的变化情况如图所示,图线上A、B、C三点对应的时刻分别为9 s、25 s和45 s,下列说法正确的是 ( )
A.上升和下落两个过程中,探测器的加速度之比为9∶16
B.探测器9 s后开始下落
C.探测器上升的最大高度为288 m
D.图中BC过程中探测器的平均速度大小为40 m/s
D
匀变速直线运动的位移与时间的关系
v-t图象所围面积的意义
位移——时间公式x=v0t+ at2的推导和应用
速度——位移公式v2–v02 =2ax的推导和应用
