4.2.1 指数函数的概念 课件(共30张PPT) 高一数学人教A版(2019)必修第一册
文档属性
| 名称 | 4.2.1 指数函数的概念 课件(共30张PPT) 高一数学人教A版(2019)必修第一册 |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-07 00:00:00 | ||
图片预览

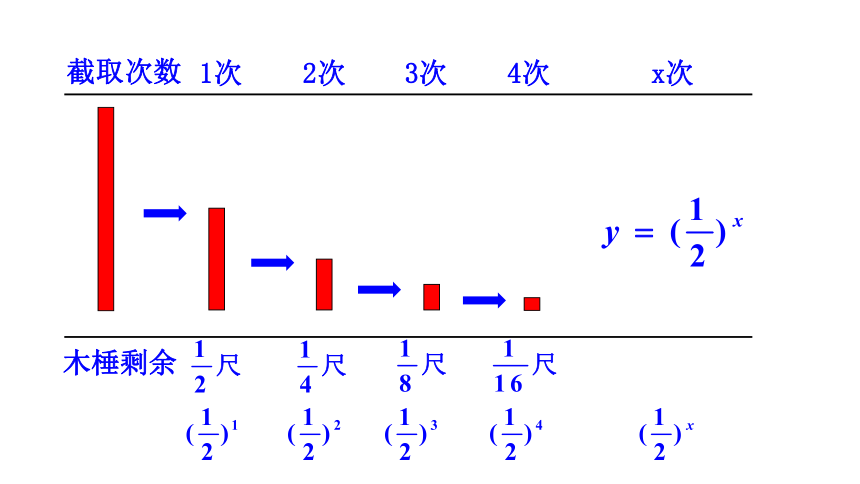









文档简介
(共30张PPT)
《庄子·天下篇》中写道:“一尺之棰,日取其半,万世不竭。”请你写出截取x次后,木棰剩余量y关于x的函数关系式?
截取次数
木棰剩余
1次
2次
3次
4次
x次
通过具体实例引入指数函数的定义,培养数学抽象的核心素养通过指数型函数的实际应用,培养数学建模的核心素养。
理解指数函数的定义,会求函数的定义域以及定区间的值域。
体会课堂探究的乐趣,
汲取新知识的营养,
让我们一起 吧!
进
走
课
堂
①底数是大于0,且不等于1的常数.
②指数是自变量x.
③ax的系数必须是1.
【解析】选C.因为函数y=(a-2)ax是指数函数,所以a-2=1,解得a=3.
C
y=N(1+p)x(x∈N)
增长
衰减
提示: 当a>1时为指数增长型函数,当01%
10%
C
【解析】选D.因为函数f(x)=(2a-3)ax是指数函数,所以2a-3=1,解得a=2.所以f(x)=2x,所以f(1)=2.
D
64
729
y=a·0.85x(x∈N*)
【解析】选C.设荷叶覆盖水面的初始面积为a,则x天后荷叶覆盖水面的面积为y=a·2x(x∈N*),根据题意,令2(a·2x)=a·220,解得x=19.
C
指数函数
的概念
核心知识
方法总结
易错提醒
核心素养
指数函数的定义
指数型函数模型
指数型函数模型公式:原有量为N,每次的增长(衰减)率为p,经过x次增长(衰减),该量增长到y,则
y=N(1±p)x(x N)
指数函数的底数大于0且不等于1
指数型函数的实际应用中,忽视自变量的取值范围
数学抽象:通过具体实例引入指数函数的定义,培养数学抽象的核心素养
数学建模:通过指数型函数的实际应用,培养数学建模的核心素养
1.下列各函数中,是指数函数的是
A.y=(-4)x B.y=-4x C.y=3x-1 D.y=
解析 A中函数的底数不满足大于零且不等于1,故不是指数函数;
B中函数式中幂值的系数不是1,故不是指数函数;
C中的指数是x-1,不是指数函数.
2.若函数y=(a2-3a+3)ax是指数函数,则( )
A.a>1且a≠1 B.a=1
C.a=1或a=2 D.a=2
【解析】若函数y=(a2-3a+3)ax是指数函数,
则a2-3a+3=1,解得a=2或a=1,
又因为指数函数的底数a>0且a≠1,故a=2.
D
定义是考查的重点
3.若函数f(x)=(4-3a)x是指数函数,则实数的取值范围是__________________.
4.据报道,某淡水湖的湖水在50年内减少了10%,若每年以相同的衰减
率呈指数衰减,按此规律,设2020年的湖水量为m,从2020年起,经过
x年后湖水量y与x的函数关系为( C )
A.y= B.y= C.y= D.y=(1-0.150x)m
解析 设每年的衰减率为q%,
则(1-q%)50=0.9,所以1-q%= ,
所以y=m·(1-q%)x= .
成功和失败本是同一片旷野,它是会令你溺水的深潭,也是能为你解渴的甘泉。
《庄子·天下篇》中写道:“一尺之棰,日取其半,万世不竭。”请你写出截取x次后,木棰剩余量y关于x的函数关系式?
截取次数
木棰剩余
1次
2次
3次
4次
x次
通过具体实例引入指数函数的定义,培养数学抽象的核心素养通过指数型函数的实际应用,培养数学建模的核心素养。
理解指数函数的定义,会求函数的定义域以及定区间的值域。
体会课堂探究的乐趣,
汲取新知识的营养,
让我们一起 吧!
进
走
课
堂
①底数是大于0,且不等于1的常数.
②指数是自变量x.
③ax的系数必须是1.
【解析】选C.因为函数y=(a-2)ax是指数函数,所以a-2=1,解得a=3.
C
y=N(1+p)x(x∈N)
增长
衰减
提示: 当a>1时为指数增长型函数,当0
10%
C
【解析】选D.因为函数f(x)=(2a-3)ax是指数函数,所以2a-3=1,解得a=2.所以f(x)=2x,所以f(1)=2.
D
64
729
y=a·0.85x(x∈N*)
【解析】选C.设荷叶覆盖水面的初始面积为a,则x天后荷叶覆盖水面的面积为y=a·2x(x∈N*),根据题意,令2(a·2x)=a·220,解得x=19.
C
指数函数
的概念
核心知识
方法总结
易错提醒
核心素养
指数函数的定义
指数型函数模型
指数型函数模型公式:原有量为N,每次的增长(衰减)率为p,经过x次增长(衰减),该量增长到y,则
y=N(1±p)x(x N)
指数函数的底数大于0且不等于1
指数型函数的实际应用中,忽视自变量的取值范围
数学抽象:通过具体实例引入指数函数的定义,培养数学抽象的核心素养
数学建模:通过指数型函数的实际应用,培养数学建模的核心素养
1.下列各函数中,是指数函数的是
A.y=(-4)x B.y=-4x C.y=3x-1 D.y=
解析 A中函数的底数不满足大于零且不等于1,故不是指数函数;
B中函数式中幂值的系数不是1,故不是指数函数;
C中的指数是x-1,不是指数函数.
2.若函数y=(a2-3a+3)ax是指数函数,则( )
A.a>1且a≠1 B.a=1
C.a=1或a=2 D.a=2
【解析】若函数y=(a2-3a+3)ax是指数函数,
则a2-3a+3=1,解得a=2或a=1,
又因为指数函数的底数a>0且a≠1,故a=2.
D
定义是考查的重点
3.若函数f(x)=(4-3a)x是指数函数,则实数的取值范围是__________________.
4.据报道,某淡水湖的湖水在50年内减少了10%,若每年以相同的衰减
率呈指数衰减,按此规律,设2020年的湖水量为m,从2020年起,经过
x年后湖水量y与x的函数关系为( C )
A.y= B.y= C.y= D.y=(1-0.150x)m
解析 设每年的衰减率为q%,
则(1-q%)50=0.9,所以1-q%= ,
所以y=m·(1-q%)x= .
成功和失败本是同一片旷野,它是会令你溺水的深潭,也是能为你解渴的甘泉。
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
