4.5.1 函数的零点与方程的解 课件(共38张PPT) 高一数学人教A版(2019)必修第一册
文档属性
| 名称 | 4.5.1 函数的零点与方程的解 课件(共38张PPT) 高一数学人教A版(2019)必修第一册 |  | |
| 格式 | ppt | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-07 23:10:14 | ||
图片预览









文档简介
(共38张PPT)
4.5 函数的应用(二)
4.5.1 函数的零点与方程的解
我国古代数学家已比较系统地解决了部分方程的求解的问题.如约公元50~100年编成的《九章算术》,就给出了求一次方程、二次方程和三次方程根的具体方法……
11世纪,北宋数学家贾宪给出了三次及三次以上的方程的解法.
13世纪,南宋数学家秦九韶给出了求任意次代数方程的正根的解法
今天我们来学习方程的根与函数的零点!
你会求什么方程的根呢?
1.理解函数零点的概念,了解函数零点与方程根的关系.(难点)
2.学习函数零点的判断方法并会判断函数零点的个数.(易错点)
3.学习掌握求函数的零点.(重点)
通过确定函数零点个数及所在区间,培养直观想象的核心素养
体会课堂探究的乐趣,
汲取新知识的营养,
让我们一起 吧!
进
走
课
堂
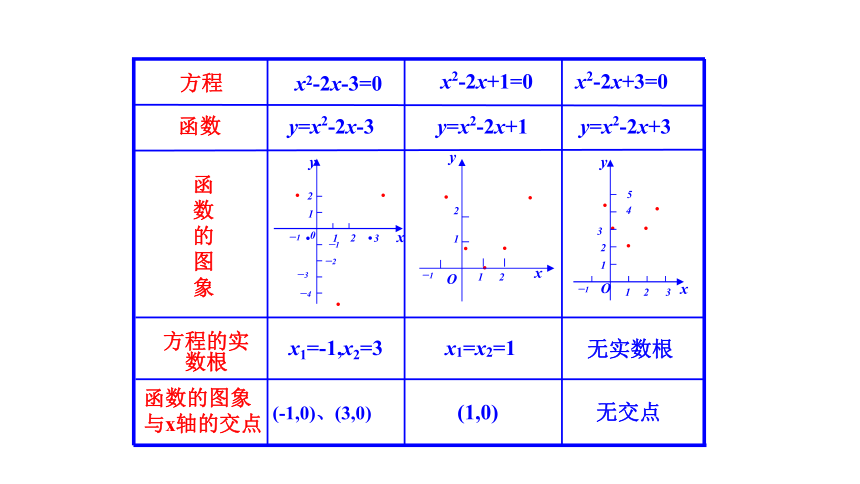
微课1:求出下列一元二次方程的根并作出相应的二次
函数的图象,观察二者有何联系?
(1)方程x2-2x-3=0与函数y=x2-2x-3
(2)方程x2-2x+1=0与函数y=x2-2x+1
(3)方程x2-2x+3=0与函数y=x2-2x+3
你知道方程对应的函数是怎么找的吗?
方程
x2-2x+1=0
x2-2x+3=0
y=x2-2x-3
y=x2-2x+1
函数
函
数
的
图
象
方程的实数根
x1=-1,x2=3
x1=x2=1
无实数根
(-1,0)、(3,0)
(1,0)
无交点
x2-2x-3=0
.
.
.
.
.
x
y
O
-1
3
2
1
1
2
5
4
3
y=x2-2x+3
函数的图象
与x轴的交点
.
.
.
.
.
y
x
-1
2
1
1
2
O
x
y
-1
3
2
1
1
2
-1
-2
-3
-4
.
.
.
.
0
.
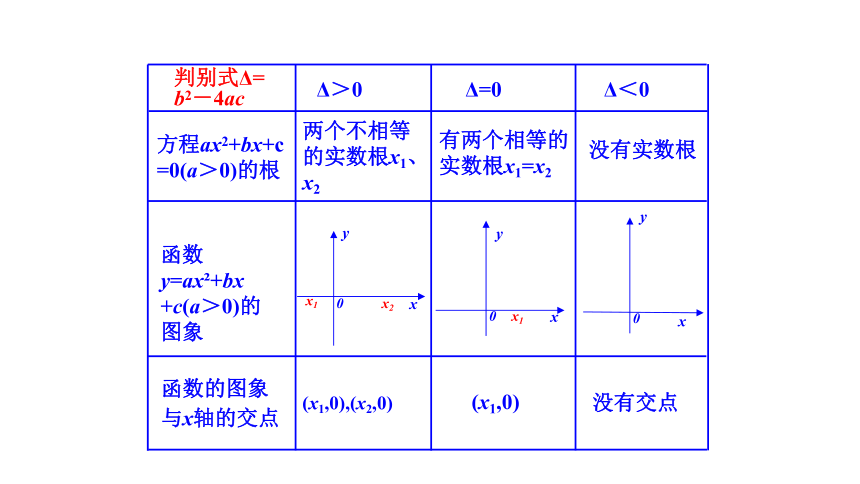
方程ax2+bx+c
=0(a>0)的根
函数y=ax +bx
+c(a>0)的图象
判别式Δ=
b2-4ac
Δ>0
Δ=0
Δ<0
函数的图象
与x轴的交点
有两个相等的
实数根x1=x2
没有实数根
x
y
x1
x2
0
x
y
0
x1
x
y
0
(x1,0),(x2,0)
(x1,0)
没有交点
两个不相等
的实数根x1、
x2
一般结论
一般地,方程f(x)=0的实数根,也就是其对应函数y=f(x)的图象与x轴交点的横坐标.
即方程f(x)=0有实数根
函数y=f(x)的图象与x轴有交点
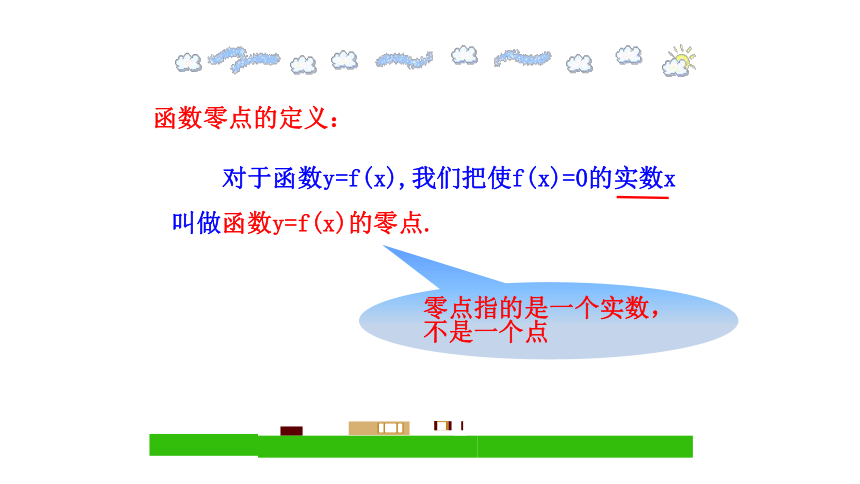
对于函数y=f(x),我们把使f(x)=0的实数x
叫做函数y=f(x)的零点.
函数零点的定义:
零点指的是一个实数,
不是一个点
方程f(x)=0有实数根
函数y=f(x)的图象与x轴有交点
函数y=f(x)有零点
结论
现在知道 如何求没有公式的方程的根了吗?
A
【即时训练】
例1 函数f(x)=x(x-4)的零点为( )
A.(0,0),(2,0) B.0
C.(4,0),(0,0), D.4,0
D
【解析】选D.由x(x-4)=0得x=0或x=4.
注意:函数的零点是实数,而不是点.
解方程是求函数零点的一种方法
B
【变式练习】
1
2
3
4
5
1
2
3
4
5
x
y
O
-1
-2
-1
-4
-3
-2
微课2:
对于不能通过求方程根的方法确定零点的函数该如何确定零点呢?
观察二次函数f(x)=x2-2x-3的图象:
在区间[-2,1]上有零点______;
f(-2)=_______,f(1)=_______,
f(-2)·f(1)___0(填“<”或“>”).
在区间(2,4)上有零点______;
f(2)·f(4)____0(填“<”或
“>”).
x=-1
-4
5
<
x=3
<
1
2
3
4
5
1
2
3
4
5
x
y
O
-2
-1
-4
-3
-2
-1
x
y
O
a
b
c
d
思考:观察图象填空
有
<
有
<
有
<
①在区间(a,b)上,f(a)·f(b)____0(填“<”或
“>”).在区间(a,b)上,______(填“有”或“无”)零
点;
②在区间(b,c)上,f(b)·f(c) ___0(填“<”或
“>”).在区间(b,c)上,______(填“有”或“无”)零
点;
③在区间(c,d)上f(c)·f(d) ___0(填“<”或
“>”).在区间(c,d)上,____(填“有”或“无”)
零点;
x
y
O
a
b
c
函数零点存在的判断
如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有f(a)·f(b)<0,那么,函数y=f(x)在区间(a,b)内有零点,即存在c∈(a,b),使得f(c)=0,这个c也就是方程f(x)=0的一个根.
方程lnx= 必有一个根的区间是( )
A.(1,2) B.(2,3)
C.( ,1) D.(3,+∞)
B
【解题关键】
将方程转化为函数,利用零点的存在性定理判断
【即时训练】
例2 判断正误,若不正确,请使用函数图象举出反例
(1)已知函数y=f(x)在区间[a,b]上连续,且f(a)·
f(b)<0,则f(x)在区间(a,b)内有且仅有一个零点.( )
(2)已知函数y=f(x)在区间[a,b]上连续,且f(a)·
f(b)≥0,则f(x)在区间(a,b)内没有零点.( )
(3)已知函数y=f(x)在区间[a,b]上满足f(a)·f(b)<0,
则f(x)在区间(a,b)内一定存在零点.( )
解析:(1)已知函数y=f (x)在区间[a,b]上连续,且
f(a)·f(b)< 0 ,则f(x)在区间(a,b)内有且仅有一
个零点. ( )
a
b
O
x
y
如图,
函数y=f(x)在区间(a,b)上有3个零点,故“在区间(a,b) 内有且仅有一个零点”的说法是错误的.
满足条件一定有零点,但不确定有几个
可知,函数y=f(x)在区间[a,b]上连续,f(a)·f(b)≥0,但f(x)在区间(a,b)内有零点.
故论断不正确.
(2)已知函数y=f(x)在区间[a,b]上连续,且
f(a)·f(b) ≥0,则f(x)在区间(a,b)内没有零点.
( )
a
b
O
x
y
如图,
虽然函数y=f(x)在区间[a,b]上满足f(a)·f(b)< 0,但是图象不是连续的曲线,则f(x)在区间(a,b)内不一定存在零点,故论断不正确.
(3)已知函数y=f(x)在区间[a,b]上满足f(a)·f(b)<0,
则f(x)在区间(a,b)内一定存在零点.( )
a
b
O
x
y
如图,
若函数y=5x2-7x-1在区间[a,b]上的图象
是连续不断的曲线,且函数y=5x2-7x-1在(a,
b)内有零点,则f(a)·f(b)的值( )
A.大于0 B.小于0
C.无法判断 D.等于0
C
【变式练习】
f(a)f(b)<0,则函数y=f(x)在(a,b)上一定有零点,
但是函数y=f(x)在(a,b)上有零点,f(a)f(b)<0不一定成立.
由表可知f(2)<0,f(3)>0,
由于函数f(x)在定义域(0,+∞)内是增函数,所以它仅有一个零点.
用计算器或计算机作出x,f(x)的对应值表和图象;
例3.求函数f(x)=lnx+2x-6的零点的个数.
解:
x 1 2 3 4 5 6 7 8 9
f(x)
-4
-1.306 9
1.098 6
3.386 3
5.609 4
7.791 8
9.945 9
12.079 4
14.197 2
方法一
f(x)=lnx+2x-6
从而f(2)·f(3)<0,∴函数f(x)在区间(2,3)内有零点.
10
8
6
4
2
-2
-4
5
1
2
3
4
6
x
y
O
y=-2x+6
y=lnx
6
O
x
1
2
3
4
y
即求方程lnx+2x-6=0的根的个数,即求lnx=6-2x的根的个数,即判断函数y=lnx与函数y=6-2x的交点个数.
如图可知,只有一个交点,即方程只有一根,函数f(x)只有一个零点.
方法二:
函数零点
方程的根
图象交点
转化
1.求方程2-x =x的根的个数,并确定根所在的区间[n,n+1](n∈Z).
解析:求方程 的根的个数,即求方程
的根的个数,即判断函数
与
的图象交点个数.由图可
知只有一个解.
y=x
1
O
x
1
2
3
4
y
【变式练习】
数形结合
估算f(x)在各整数处的取值的正负:
令
由上表可知,方程的根所在区间为
x 0 1 2 3
f(x)
-
+
+
+
可根据图象确定大体区间
C
函数的零点
与方程的解
核心知识
方法总结
易错提醒
核心素养
直观想象:通过确定函数零点个数及所在区间,培养直观想象的核心素养
应用函数零点存在定理时注意函数图象的连续性
数形结合:借助函数图象与x轴交点确定零点及方程的根
转化法:函数的零点转化为方程的根,转化为函数图象与x轴的交点
函数零点的定义
函数零点、方程的根、函数的图象与x轴交点的关系
函数的零点存在定理
1.在二次函数 中,ac<0,则其零点的个
数为( )
A.1 B.2 C.3 D.不存在
2.若 不是常数函数且最小值为1,则
的零点个数( )
A.0
B.1
C.0或1
D.不确定
D
B
(-∞,0)∪(0,1)∪(1,+∞)
1
3
6.若方程ax2-x-1=0在(0,1)内恰有一个零点,求实数a的取值范围.
【解析】 (1)当a=0时,f(x)=-x-1,其零点为-1 (0,1),所以a≠0; (2)当a≠0时,因为方程ax2-x-1=0在(0,1)内恰有一解,即二次函数f(x)=ax2-x-1在(0,1)内恰有一个零点,所以f(0) f(1)<0, 即-1×(a-2)<0,解得a>2.
故a的取值范围为(2,+∞).
如果你不知道你要到哪儿去,那通常你哪儿也去不了.
4.5 函数的应用(二)
4.5.1 函数的零点与方程的解
我国古代数学家已比较系统地解决了部分方程的求解的问题.如约公元50~100年编成的《九章算术》,就给出了求一次方程、二次方程和三次方程根的具体方法……
11世纪,北宋数学家贾宪给出了三次及三次以上的方程的解法.
13世纪,南宋数学家秦九韶给出了求任意次代数方程的正根的解法
今天我们来学习方程的根与函数的零点!
你会求什么方程的根呢?
1.理解函数零点的概念,了解函数零点与方程根的关系.(难点)
2.学习函数零点的判断方法并会判断函数零点的个数.(易错点)
3.学习掌握求函数的零点.(重点)
通过确定函数零点个数及所在区间,培养直观想象的核心素养
体会课堂探究的乐趣,
汲取新知识的营养,
让我们一起 吧!
进
走
课
堂
微课1:求出下列一元二次方程的根并作出相应的二次
函数的图象,观察二者有何联系?
(1)方程x2-2x-3=0与函数y=x2-2x-3
(2)方程x2-2x+1=0与函数y=x2-2x+1
(3)方程x2-2x+3=0与函数y=x2-2x+3
你知道方程对应的函数是怎么找的吗?
方程
x2-2x+1=0
x2-2x+3=0
y=x2-2x-3
y=x2-2x+1
函数
函
数
的
图
象
方程的实数根
x1=-1,x2=3
x1=x2=1
无实数根
(-1,0)、(3,0)
(1,0)
无交点
x2-2x-3=0
.
.
.
.
.
x
y
O
-1
3
2
1
1
2
5
4
3
y=x2-2x+3
函数的图象
与x轴的交点
.
.
.
.
.
y
x
-1
2
1
1
2
O
x
y
-1
3
2
1
1
2
-1
-2
-3
-4
.
.
.
.
0
.
方程ax2+bx+c
=0(a>0)的根
函数y=ax +bx
+c(a>0)的图象
判别式Δ=
b2-4ac
Δ>0
Δ=0
Δ<0
函数的图象
与x轴的交点
有两个相等的
实数根x1=x2
没有实数根
x
y
x1
x2
0
x
y
0
x1
x
y
0
(x1,0),(x2,0)
(x1,0)
没有交点
两个不相等
的实数根x1、
x2
一般结论
一般地,方程f(x)=0的实数根,也就是其对应函数y=f(x)的图象与x轴交点的横坐标.
即方程f(x)=0有实数根
函数y=f(x)的图象与x轴有交点
对于函数y=f(x),我们把使f(x)=0的实数x
叫做函数y=f(x)的零点.
函数零点的定义:
零点指的是一个实数,
不是一个点
方程f(x)=0有实数根
函数y=f(x)的图象与x轴有交点
函数y=f(x)有零点
结论
现在知道 如何求没有公式的方程的根了吗?
A
【即时训练】
例1 函数f(x)=x(x-4)的零点为( )
A.(0,0),(2,0) B.0
C.(4,0),(0,0), D.4,0
D
【解析】选D.由x(x-4)=0得x=0或x=4.
注意:函数的零点是实数,而不是点.
解方程是求函数零点的一种方法
B
【变式练习】
1
2
3
4
5
1
2
3
4
5
x
y
O
-1
-2
-1
-4
-3
-2
微课2:
对于不能通过求方程根的方法确定零点的函数该如何确定零点呢?
观察二次函数f(x)=x2-2x-3的图象:
在区间[-2,1]上有零点______;
f(-2)=_______,f(1)=_______,
f(-2)·f(1)___0(填“<”或“>”).
在区间(2,4)上有零点______;
f(2)·f(4)____0(填“<”或
“>”).
x=-1
-4
5
<
x=3
<
1
2
3
4
5
1
2
3
4
5
x
y
O
-2
-1
-4
-3
-2
-1
x
y
O
a
b
c
d
思考:观察图象填空
有
<
有
<
有
<
①在区间(a,b)上,f(a)·f(b)____0(填“<”或
“>”).在区间(a,b)上,______(填“有”或“无”)零
点;
②在区间(b,c)上,f(b)·f(c) ___0(填“<”或
“>”).在区间(b,c)上,______(填“有”或“无”)零
点;
③在区间(c,d)上f(c)·f(d) ___0(填“<”或
“>”).在区间(c,d)上,____(填“有”或“无”)
零点;
x
y
O
a
b
c
函数零点存在的判断
如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有f(a)·f(b)<0,那么,函数y=f(x)在区间(a,b)内有零点,即存在c∈(a,b),使得f(c)=0,这个c也就是方程f(x)=0的一个根.
方程lnx= 必有一个根的区间是( )
A.(1,2) B.(2,3)
C.( ,1) D.(3,+∞)
B
【解题关键】
将方程转化为函数,利用零点的存在性定理判断
【即时训练】
例2 判断正误,若不正确,请使用函数图象举出反例
(1)已知函数y=f(x)在区间[a,b]上连续,且f(a)·
f(b)<0,则f(x)在区间(a,b)内有且仅有一个零点.( )
(2)已知函数y=f(x)在区间[a,b]上连续,且f(a)·
f(b)≥0,则f(x)在区间(a,b)内没有零点.( )
(3)已知函数y=f(x)在区间[a,b]上满足f(a)·f(b)<0,
则f(x)在区间(a,b)内一定存在零点.( )
解析:(1)已知函数y=f (x)在区间[a,b]上连续,且
f(a)·f(b)< 0 ,则f(x)在区间(a,b)内有且仅有一
个零点. ( )
a
b
O
x
y
如图,
函数y=f(x)在区间(a,b)上有3个零点,故“在区间(a,b) 内有且仅有一个零点”的说法是错误的.
满足条件一定有零点,但不确定有几个
可知,函数y=f(x)在区间[a,b]上连续,f(a)·f(b)≥0,但f(x)在区间(a,b)内有零点.
故论断不正确.
(2)已知函数y=f(x)在区间[a,b]上连续,且
f(a)·f(b) ≥0,则f(x)在区间(a,b)内没有零点.
( )
a
b
O
x
y
如图,
虽然函数y=f(x)在区间[a,b]上满足f(a)·f(b)< 0,但是图象不是连续的曲线,则f(x)在区间(a,b)内不一定存在零点,故论断不正确.
(3)已知函数y=f(x)在区间[a,b]上满足f(a)·f(b)<0,
则f(x)在区间(a,b)内一定存在零点.( )
a
b
O
x
y
如图,
若函数y=5x2-7x-1在区间[a,b]上的图象
是连续不断的曲线,且函数y=5x2-7x-1在(a,
b)内有零点,则f(a)·f(b)的值( )
A.大于0 B.小于0
C.无法判断 D.等于0
C
【变式练习】
f(a)f(b)<0,则函数y=f(x)在(a,b)上一定有零点,
但是函数y=f(x)在(a,b)上有零点,f(a)f(b)<0不一定成立.
由表可知f(2)<0,f(3)>0,
由于函数f(x)在定义域(0,+∞)内是增函数,所以它仅有一个零点.
用计算器或计算机作出x,f(x)的对应值表和图象;
例3.求函数f(x)=lnx+2x-6的零点的个数.
解:
x 1 2 3 4 5 6 7 8 9
f(x)
-4
-1.306 9
1.098 6
3.386 3
5.609 4
7.791 8
9.945 9
12.079 4
14.197 2
方法一
f(x)=lnx+2x-6
从而f(2)·f(3)<0,∴函数f(x)在区间(2,3)内有零点.
10
8
6
4
2
-2
-4
5
1
2
3
4
6
x
y
O
y=-2x+6
y=lnx
6
O
x
1
2
3
4
y
即求方程lnx+2x-6=0的根的个数,即求lnx=6-2x的根的个数,即判断函数y=lnx与函数y=6-2x的交点个数.
如图可知,只有一个交点,即方程只有一根,函数f(x)只有一个零点.
方法二:
函数零点
方程的根
图象交点
转化
1.求方程2-x =x的根的个数,并确定根所在的区间[n,n+1](n∈Z).
解析:求方程 的根的个数,即求方程
的根的个数,即判断函数
与
的图象交点个数.由图可
知只有一个解.
y=x
1
O
x
1
2
3
4
y
【变式练习】
数形结合
估算f(x)在各整数处的取值的正负:
令
由上表可知,方程的根所在区间为
x 0 1 2 3
f(x)
-
+
+
+
可根据图象确定大体区间
C
函数的零点
与方程的解
核心知识
方法总结
易错提醒
核心素养
直观想象:通过确定函数零点个数及所在区间,培养直观想象的核心素养
应用函数零点存在定理时注意函数图象的连续性
数形结合:借助函数图象与x轴交点确定零点及方程的根
转化法:函数的零点转化为方程的根,转化为函数图象与x轴的交点
函数零点的定义
函数零点、方程的根、函数的图象与x轴交点的关系
函数的零点存在定理
1.在二次函数 中,ac<0,则其零点的个
数为( )
A.1 B.2 C.3 D.不存在
2.若 不是常数函数且最小值为1,则
的零点个数( )
A.0
B.1
C.0或1
D.不确定
D
B
(-∞,0)∪(0,1)∪(1,+∞)
1
3
6.若方程ax2-x-1=0在(0,1)内恰有一个零点,求实数a的取值范围.
【解析】 (1)当a=0时,f(x)=-x-1,其零点为-1 (0,1),所以a≠0; (2)当a≠0时,因为方程ax2-x-1=0在(0,1)内恰有一解,即二次函数f(x)=ax2-x-1在(0,1)内恰有一个零点,所以f(0) f(1)<0, 即-1×(a-2)<0,解得a>2.
故a的取值范围为(2,+∞).
如果你不知道你要到哪儿去,那通常你哪儿也去不了.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
