5.1.2 弧度制 课件(共32张PPT) 高一数学人教A版(2019)必修第一册
文档属性
| 名称 | 5.1.2 弧度制 课件(共32张PPT) 高一数学人教A版(2019)必修第一册 |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-07 23:16:48 | ||
图片预览










文档简介
(共32张PPT)
5.1.2 弧度制
思 考
有人问:上海到南京有多远时,有人回答约300公里,但也有人回答约188英里,请问哪一种回答是正确的?(已知1英里=1.6公里)
1.掌握弧度制的定义.
2.学会弧度与角度的互化.(重点)
3.会推导弧度制下的弧长公式及扇形的面积
公式.(重点、难点)
4.熟记特殊角的弧度数.
1.通过扇形的弧长公式和面积公式的运用,培养数 学运算的核心素养(数学运算)
体会课堂探究的乐趣,
汲取新知识的营养,
让我们一起 吧!
进
走
课
堂
思考:每个小组发一个硬纸做成的圆形图片,一段细铁丝,让学生测量在不同的圆中, 等于半径长的圆弧所对圆心角,并观察所得到的结果有什么规律?
提示:大小相等
微课1 弧度制
把长度等于半径长的弧所对的圆心角叫做1弧度(radian)的角,用符号rad表示,读作弧度.
弧度的概念
规定:正角的弧度数为正数,负角的弧度数为负数,零角的弧度数为0;
r
l=r
O
A
B
如果半径为r的圆的圆心角α所对的弧长为l,那么,角α的弧度数的绝对值是
将分针拨快15分钟,则分针转过的弧度数是 ( )
A. B.
C. D.
C
【即时训练】
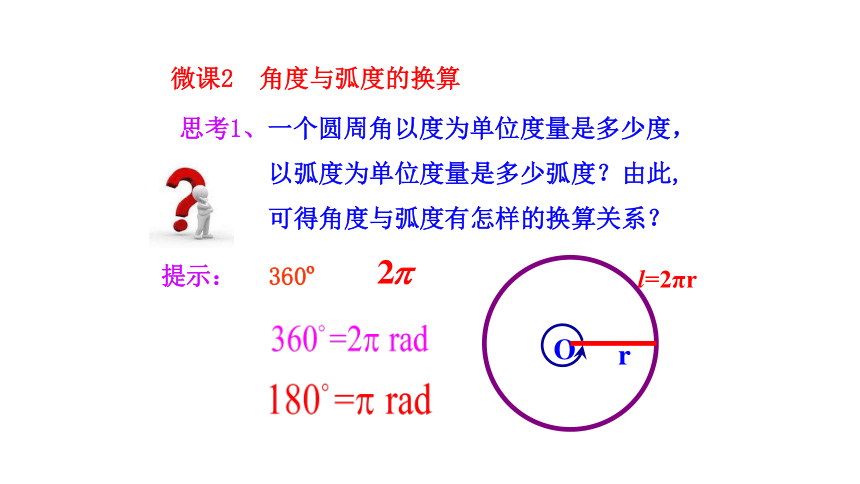
微课2 角度与弧度的换算
思考1、一个圆周角以度为单位度量是多少度,
以弧度为单位度量是多少弧度?由此,
可得角度与弧度有怎样的换算关系?
360
l=2πr
O
r
提示:
思考2、根据上述关系,1°等于多少弧度,1 rad等于多少度?
提示:
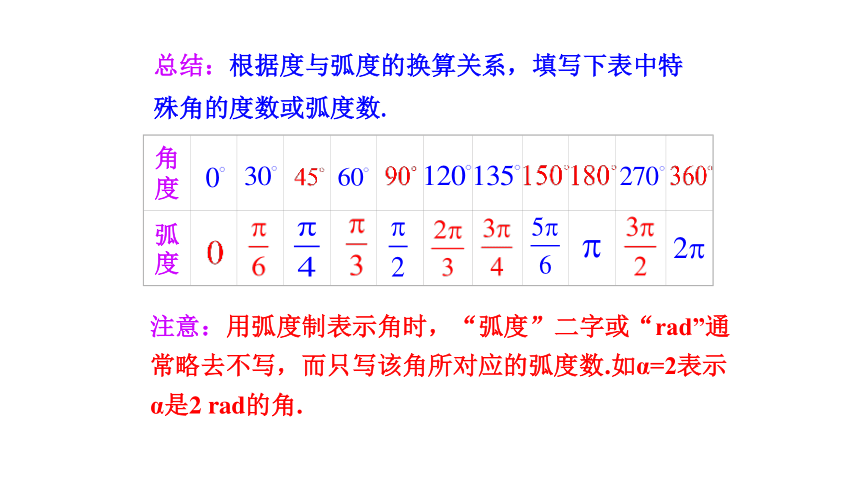
总结:根据度与弧度的换算关系,填写下表中特殊角的度数或弧度数.
注意:用弧度制表示角时,“弧度”二字或“rad”通常略去不写,而只写该角所对应的弧度数.如α=2表示α是2 rad的角.
角度
弧度
弧度制下角的集合与实数集的一一对应:
正角
零角
负角
正实数
零
负实数
任意角的集合
实数集R
15
30
-157
390
【即时训练】
思考1、已知一个扇形所在圆的半径为r,弧长为l,圆心角为α,那么扇形的面积如何计算?
提示:
微课3 弧度制的应用
思考2、在弧度制下,与角α终边相同的角如何表示?终边在坐标轴上的角如何表示?
终边在x轴上:
终边在y轴上:
提示:
D
【即时训练】
例1.按照下列要求,把 67°30′化成弧度:
(1)精确值; (2)精确到0.001的近似值.
(2)利用计算器有
MODE MODE 2
67 。, ,, 30 。, ,, SHIFT DRG 1 =
1.178 097 245.因此,67°30′≈1.178 rad.
【变式练习】
例2.将3.14 rad换算成角度(用度数表示,精确到0.001).
解:利用计算器
MODE MODE 1
3.14 SHIFT DRG 2 = 179.908 747 7.
因此,3.14 rad≈179.909°.
航海罗盘的圆周被分成32等份,把每一等份所对的圆心角的大小分别用度与弧度表示出来.
11.25°,
【变式练习】
证明:由公式 可得,
由于半径为R,圆心角为n°的扇形的弧长公式和面积公式 分别是:
将n°转换为弧度,得 于是,
将 代入上式,即得
例3.利用弧度制证明下列关于扇形的公式:
其中R是半径,l是弧长, 为圆心角,
S是扇形的面积.
一个半径为R的扇形,它的周长为4R,则这扇形的面积为( )
A.2 B.2
C. D.
D
【变式练习】
解:由计算器 2
MODE
MODE
sin
=
1.5
0.997 494 986
MODE
MODE
1
sin
。, , ,
85
0.996 194 698.
=
所以 sin 1.5>sin 85°.
例4.利用计算器比较sin 1.5和sin 85°的大小.
5 弧度的角所在的象限为( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
D
【变式练习】
1.1弧度角的定义;
2.“角度制”与“弧度制”的联系与区别;
3.弧长公式与扇形面积公式.
一、回顾本节课的收获
弧度制 角度制
度量单位 弧度 角度
单位规定 等于半径的长的圆弧所对应的圆心角叫1 rad 的角
周角的
为1度的角
换算关系
πrad=180°
1rad=
57°18′
1°=
rad=0.01745 rad
二、弧度制与角度制的比较
弧度制
核心知识
方法总结
易错提醒
核心素养
弧度制的概念
弧度制的计算及与角度制的互化
扇形的弧长和面积公式
弧度制表示角时,先将分、秒化成度,再化为弧度
根据已知图形写出区域角的集合时,先写始边和终边对应的角
数学运算:通过扇形的弧长公式和面积公式的运用,培养数学运算的核心素养
同一个式子中角度制与弧度制不能混用
写出区域角时注意始边和终边的虚实
C
不相等
相等
把希望建筑在意欲和心愿上面的人们,二十次中有十九次都会失望.
——大仲马
5.1.2 弧度制
思 考
有人问:上海到南京有多远时,有人回答约300公里,但也有人回答约188英里,请问哪一种回答是正确的?(已知1英里=1.6公里)
1.掌握弧度制的定义.
2.学会弧度与角度的互化.(重点)
3.会推导弧度制下的弧长公式及扇形的面积
公式.(重点、难点)
4.熟记特殊角的弧度数.
1.通过扇形的弧长公式和面积公式的运用,培养数 学运算的核心素养(数学运算)
体会课堂探究的乐趣,
汲取新知识的营养,
让我们一起 吧!
进
走
课
堂
思考:每个小组发一个硬纸做成的圆形图片,一段细铁丝,让学生测量在不同的圆中, 等于半径长的圆弧所对圆心角,并观察所得到的结果有什么规律?
提示:大小相等
微课1 弧度制
把长度等于半径长的弧所对的圆心角叫做1弧度(radian)的角,用符号rad表示,读作弧度.
弧度的概念
规定:正角的弧度数为正数,负角的弧度数为负数,零角的弧度数为0;
r
l=r
O
A
B
如果半径为r的圆的圆心角α所对的弧长为l,那么,角α的弧度数的绝对值是
将分针拨快15分钟,则分针转过的弧度数是 ( )
A. B.
C. D.
C
【即时训练】
微课2 角度与弧度的换算
思考1、一个圆周角以度为单位度量是多少度,
以弧度为单位度量是多少弧度?由此,
可得角度与弧度有怎样的换算关系?
360
l=2πr
O
r
提示:
思考2、根据上述关系,1°等于多少弧度,1 rad等于多少度?
提示:
总结:根据度与弧度的换算关系,填写下表中特殊角的度数或弧度数.
注意:用弧度制表示角时,“弧度”二字或“rad”通常略去不写,而只写该角所对应的弧度数.如α=2表示α是2 rad的角.
角度
弧度
弧度制下角的集合与实数集的一一对应:
正角
零角
负角
正实数
零
负实数
任意角的集合
实数集R
15
30
-157
390
【即时训练】
思考1、已知一个扇形所在圆的半径为r,弧长为l,圆心角为α,那么扇形的面积如何计算?
提示:
微课3 弧度制的应用
思考2、在弧度制下,与角α终边相同的角如何表示?终边在坐标轴上的角如何表示?
终边在x轴上:
终边在y轴上:
提示:
D
【即时训练】
例1.按照下列要求,把 67°30′化成弧度:
(1)精确值; (2)精确到0.001的近似值.
(2)利用计算器有
MODE MODE 2
67 。, ,, 30 。, ,, SHIFT DRG 1 =
1.178 097 245.因此,67°30′≈1.178 rad.
【变式练习】
例2.将3.14 rad换算成角度(用度数表示,精确到0.001).
解:利用计算器
MODE MODE 1
3.14 SHIFT DRG 2 = 179.908 747 7.
因此,3.14 rad≈179.909°.
航海罗盘的圆周被分成32等份,把每一等份所对的圆心角的大小分别用度与弧度表示出来.
11.25°,
【变式练习】
证明:由公式 可得,
由于半径为R,圆心角为n°的扇形的弧长公式和面积公式 分别是:
将n°转换为弧度,得 于是,
将 代入上式,即得
例3.利用弧度制证明下列关于扇形的公式:
其中R是半径,l是弧长, 为圆心角,
S是扇形的面积.
一个半径为R的扇形,它的周长为4R,则这扇形的面积为( )
A.2 B.2
C. D.
D
【变式练习】
解:由计算器 2
MODE
MODE
sin
=
1.5
0.997 494 986
MODE
MODE
1
sin
。, , ,
85
0.996 194 698.
=
所以 sin 1.5>sin 85°.
例4.利用计算器比较sin 1.5和sin 85°的大小.
5 弧度的角所在的象限为( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
D
【变式练习】
1.1弧度角的定义;
2.“角度制”与“弧度制”的联系与区别;
3.弧长公式与扇形面积公式.
一、回顾本节课的收获
弧度制 角度制
度量单位 弧度 角度
单位规定 等于半径的长的圆弧所对应的圆心角叫1 rad 的角
周角的
为1度的角
换算关系
πrad=180°
1rad=
57°18′
1°=
rad=0.01745 rad
二、弧度制与角度制的比较
弧度制
核心知识
方法总结
易错提醒
核心素养
弧度制的概念
弧度制的计算及与角度制的互化
扇形的弧长和面积公式
弧度制表示角时,先将分、秒化成度,再化为弧度
根据已知图形写出区域角的集合时,先写始边和终边对应的角
数学运算:通过扇形的弧长公式和面积公式的运用,培养数学运算的核心素养
同一个式子中角度制与弧度制不能混用
写出区域角时注意始边和终边的虚实
C
不相等
相等
把希望建筑在意欲和心愿上面的人们,二十次中有十九次都会失望.
——大仲马
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
