1.3 第2课时 正方形的判定 课件(共23张PPT) 北师版九年级上册
文档属性
| 名称 | 1.3 第2课时 正方形的判定 课件(共23张PPT) 北师版九年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 337.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-08 00:00:00 | ||
图片预览



文档简介
(共23张PPT)
1.3 正方形的性质与判定
北师版九年级上册 第一章
课程讲授
课程导入
习题解析
课堂总结
第二课时 正方形的判定
前 言
学习目标及重难点
1.探索并证明正方形的判定,了解平行四边形、矩形、菱形之间的联系和区别;(重点)
2.会运用正方形的判定条件进行有关的论证和计算 .(难点)
课程导入
什么是正方形?
正方形有哪些性质?
有一组邻边相等,并且有一个角是直角的平行四边形叫做正方形.
1.正方形的四个角都是直角,四条边相等.
2.正方形的两条对角线相等且互相垂直平分.
课程讲授
新课推进
探索1:正方形的判定
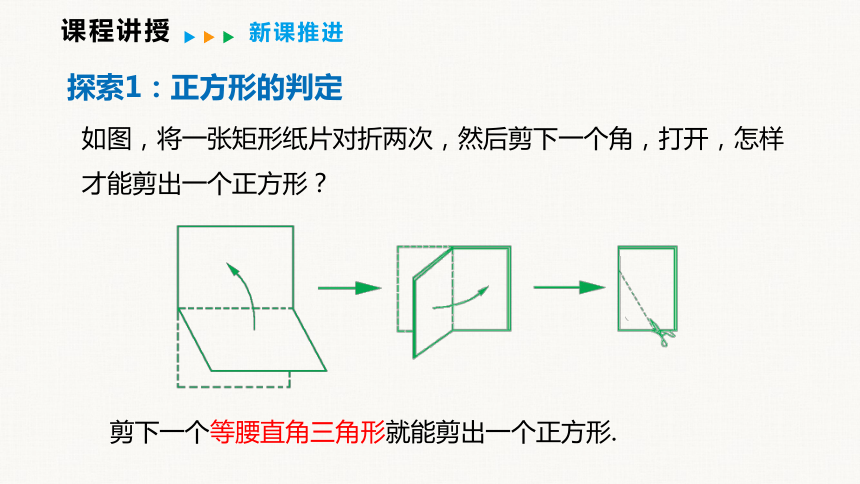
如图,将一张矩形纸片对折两次,然后剪下一个角,打开,怎样才能剪出一个正方形?
剪下一个等腰直角三角形就能剪出一个正方形.
课程讲授
新课推进
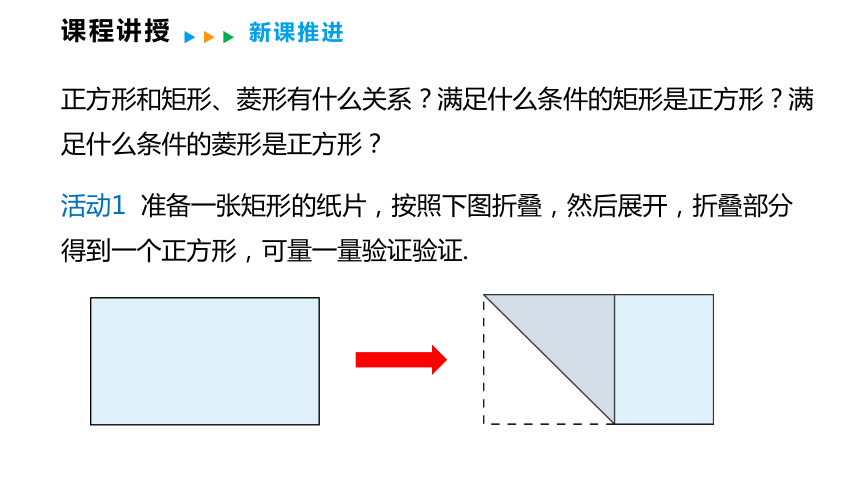
正方形和矩形、菱形有什么关系?满足什么条件的矩形是正方形?满足什么条件的菱形是正方形?
活动1 准备一张矩形的纸片,按照下图折叠,然后展开,折叠部分得到一个正方形,可量一量验证验证.
课程讲授
新课推进
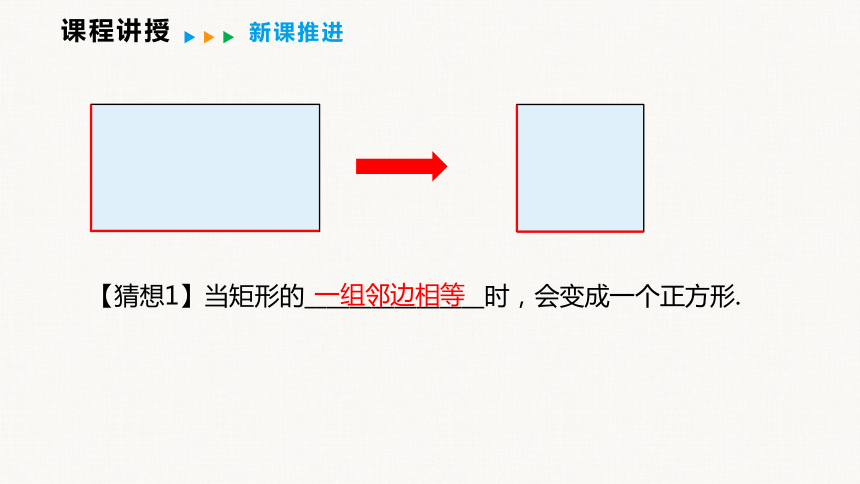
【猜想1】当矩形的________________时,会变成一个正方形.
一组邻边相等
课程讲授
新课推进
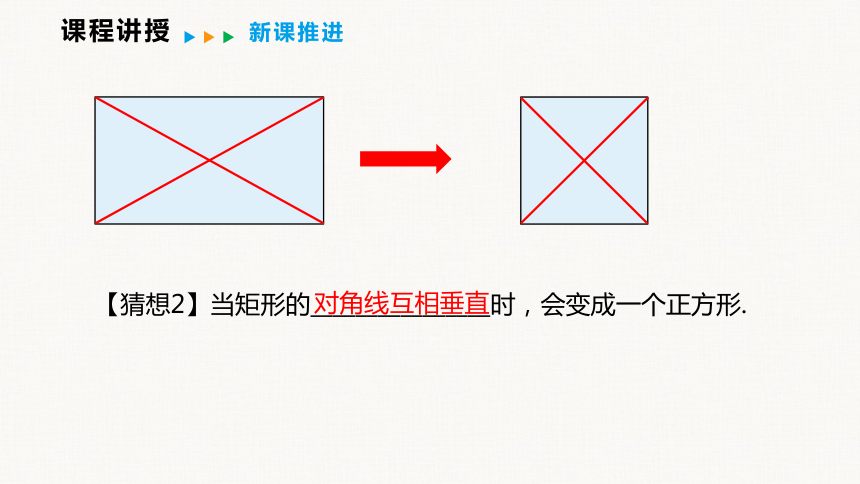
【猜想2】当矩形的________________时,会变成一个正方形.
对角线互相垂直
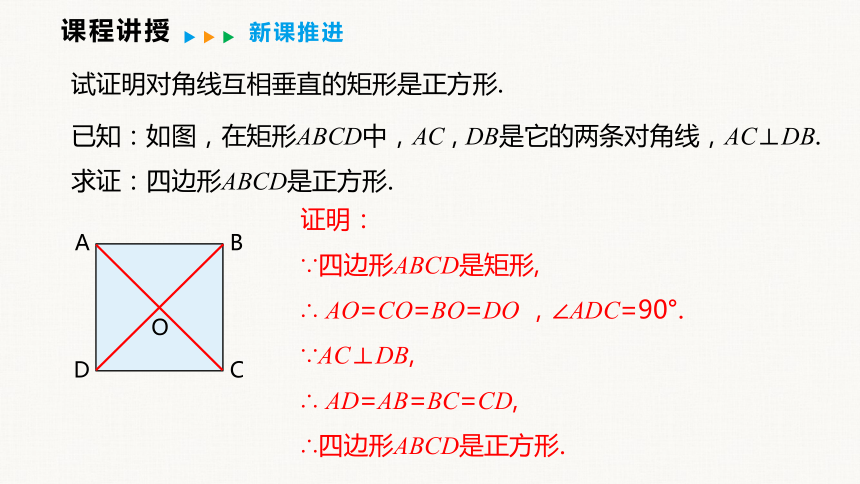
试证明对角线互相垂直的矩形是正方形.
已知:如图,在矩形ABCD中,AC , DB是它的两条对角线,AC⊥DB.
求证:四边形ABCD是正方形.
A
B
C
D
O
证明:
∵四边形ABCD是矩形,
∴ AO=CO=BO=DO ,∠ADC=90°.
∵AC⊥DB,
∴ AD=AB=BC=CD,
∴四边形ABCD是正方形.
课程讲授
新课推进
课程讲授
新课推进
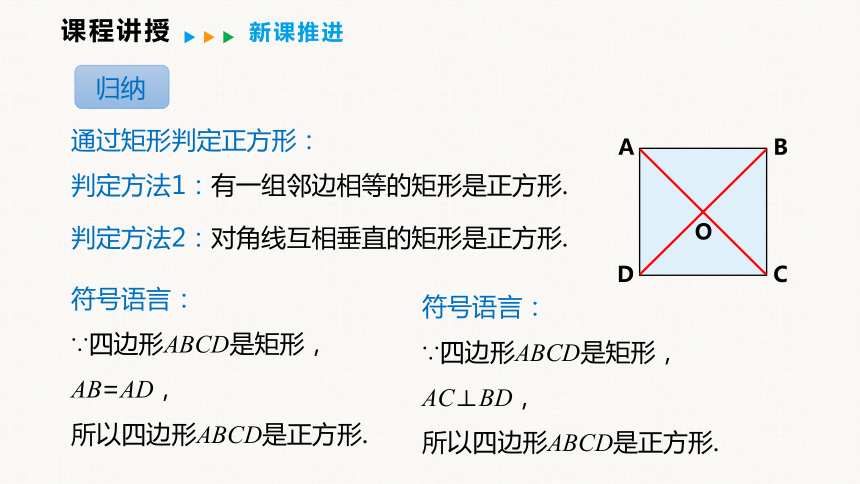
归纳
通过矩形判定正方形:
判定方法1:有一组邻边相等的矩形是正方形.
符号语言:
∵四边形ABCD是矩形,
AB=AD,
所以四边形ABCD是正方形.
判定方法2:对角线互相垂直的矩形是正方形.
符号语言:
∵四边形ABCD是矩形,
AC⊥BD,
所以四边形ABCD是正方形.
A
B
C
D
O
满足什么条件的菱形是正方形?
【猜想1】当菱形的________________时,会变成一个正方形.
一个角是直角
课程讲授
新课推进
课程讲授
新课推进
满足什么条件的菱形是正方形?
【猜想2】当菱形的________________时,会变成一个正方形.
对角线相等
试证明对角线相等的菱形是正方形.
已知:如图,在菱形ABCD中,AC , DB是它的两条对角线,AC=DB.
求证:四边形ABCD是正方形.
A
B
C
D
O
课程讲授
新课推进
课程讲授
新课推进
通过菱形判定正方形:
判定方法1:有一个角是直角的菱形是正方形.
符号语言:
∵四边形ABCD是菱形,
∠ABC=90°,
所以四边形ABCD是正方形.
判定方法2:对角线相等的菱形是正方形.
符号语言:
∵四边形ABCD是菱形,
AC=BD,
所以四边形ABCD是正方形.
A
B
C
D
O
归纳
课程讲授
新课推进
已知:如图,在矩形ABCD中,BE平分∠ABC,CE平分∠DCB,BF∥CE,CF∥BE. 求证:四边形BECF是正方形.
思考:通过什么方式证明四边形BECF是正方形?
思路一:先证明四边形BECF是菱形,然后证明四边形BECF中有一个角是直角;
思路二:先证明四边形BECF是矩形,然后证明四边形BECF中有一组邻边相等.
例1
课程讲授
新课推进
【思路二】
证明:∵四边形ABCD是矩形,∴∠ABC=∠DCB=90°.
∵BE平分∠ABC,CE平分∠DCB,∴∠EBC = 45°, ∠ECB = 45°, ∴ ∠EBC=∠ECB=45°,∴EB=EC. ∵BF∥CE,CF ∥BE,
∴∠FBC=∠ECB=45°,∠FCB=∠EBC=45°,
∴∠EBF=∠ECF=∠BEC=90°,∴矩形BECF是正方形.
课程讲授
新课推进
我们知道,任意画一个四边形,以四边的中点为顶点可以组成一个平行四边形.
任意画一个正方形,以四边的中点为顶点可以组成一个怎样的图形呢?先猜一猜,再证明.
A
D
C
B
A1
B1
C1
D1
以正方形四边的中点为顶点,可以组成一个正方形.
证明思路:
利用三角形的中位线证出A1D1=A1B1=C1D1
=C1B1,从而得到四边形A1B1C1D1是矩形,再根据一组邻边相等得出A1B1C1D1是正方形.
课程讲授
新课推进
习题解析
习题1
下列说法正确的是( )
A.一组对边平行另一组对边相等的四边形是平行四边形
B.对角线互相垂直平分的四边形是菱形
C.对角线相等的四边形是矩形
D.对角线互相垂直且相等的四边形是正方形
B
习题解析
习题2
如图,在△ABC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且BE=BF,添加一个条件,仍不能证明四边形BECF为正方形的是( )
A.BC=AC
B.BD=DF
C.AC=BF
D.CF⊥BF
C
习题3
习题解析
如图,在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.
(1)求证:△BED≌△CFD;
证明:∵DE⊥AB,DF⊥AC,
∴∠BED=∠CFD=90°.
∵AB=AC,∴∠B=∠C.
∵D是BC的中点,
∴BD=CD.
∴△BED≌△CFD.
习题解析
(2)若∠A=90°,求证:四边形DFAE是正方形.
解:∵DE⊥AB,DF⊥AC,
∴∠AED=∠AFD=90°.
又∵∠A=90°,∴四边形DFAE为矩形.
由(1)知,△BED≌△CFD,
∴DE=DF.
∴四边形DFAE是正方形.
习题解析
拓展提升
如图,等边三角形AEF的顶点E,F分别在矩形ABCD的边BC,CD上,且∠CEF=45°.
求证:矩形ABCD是正方形.
证明:∵四边形ABCD是矩形,∴∠B=∠D=∠C=90°.
∵△AEF是等边三角形,∴AE=AF,∠AEF=∠AFE=60°.
∵∠CEF=45°,∴∠CFE=∠CEF=45°.
∴∠AFD=∠AEB=180°-45°-60°=75°.
∴△ABE≌△ADF(AAS).∴AB=AD.
∴矩形ABCD是正方形.
课程总结
小结
5种判定方法
三个角是直角
四条边相等
一个角是直角
或对角线相等
一组邻边相等
或对角线垂直
一组邻边相等
或对角线垂直
一个角是直角
或对角线相等
一个角是直角且一组邻边相等
平行四边形、矩形、菱形、正方形的判定小结
1.3 正方形的性质与判定
北师版九年级上册 第一章
课程讲授
课程导入
习题解析
课堂总结
第二课时 正方形的判定
前 言
学习目标及重难点
1.探索并证明正方形的判定,了解平行四边形、矩形、菱形之间的联系和区别;(重点)
2.会运用正方形的判定条件进行有关的论证和计算 .(难点)
课程导入
什么是正方形?
正方形有哪些性质?
有一组邻边相等,并且有一个角是直角的平行四边形叫做正方形.
1.正方形的四个角都是直角,四条边相等.
2.正方形的两条对角线相等且互相垂直平分.
课程讲授
新课推进
探索1:正方形的判定
如图,将一张矩形纸片对折两次,然后剪下一个角,打开,怎样才能剪出一个正方形?
剪下一个等腰直角三角形就能剪出一个正方形.
课程讲授
新课推进
正方形和矩形、菱形有什么关系?满足什么条件的矩形是正方形?满足什么条件的菱形是正方形?
活动1 准备一张矩形的纸片,按照下图折叠,然后展开,折叠部分得到一个正方形,可量一量验证验证.
课程讲授
新课推进
【猜想1】当矩形的________________时,会变成一个正方形.
一组邻边相等
课程讲授
新课推进
【猜想2】当矩形的________________时,会变成一个正方形.
对角线互相垂直
试证明对角线互相垂直的矩形是正方形.
已知:如图,在矩形ABCD中,AC , DB是它的两条对角线,AC⊥DB.
求证:四边形ABCD是正方形.
A
B
C
D
O
证明:
∵四边形ABCD是矩形,
∴ AO=CO=BO=DO ,∠ADC=90°.
∵AC⊥DB,
∴ AD=AB=BC=CD,
∴四边形ABCD是正方形.
课程讲授
新课推进
课程讲授
新课推进
归纳
通过矩形判定正方形:
判定方法1:有一组邻边相等的矩形是正方形.
符号语言:
∵四边形ABCD是矩形,
AB=AD,
所以四边形ABCD是正方形.
判定方法2:对角线互相垂直的矩形是正方形.
符号语言:
∵四边形ABCD是矩形,
AC⊥BD,
所以四边形ABCD是正方形.
A
B
C
D
O
满足什么条件的菱形是正方形?
【猜想1】当菱形的________________时,会变成一个正方形.
一个角是直角
课程讲授
新课推进
课程讲授
新课推进
满足什么条件的菱形是正方形?
【猜想2】当菱形的________________时,会变成一个正方形.
对角线相等
试证明对角线相等的菱形是正方形.
已知:如图,在菱形ABCD中,AC , DB是它的两条对角线,AC=DB.
求证:四边形ABCD是正方形.
A
B
C
D
O
课程讲授
新课推进
课程讲授
新课推进
通过菱形判定正方形:
判定方法1:有一个角是直角的菱形是正方形.
符号语言:
∵四边形ABCD是菱形,
∠ABC=90°,
所以四边形ABCD是正方形.
判定方法2:对角线相等的菱形是正方形.
符号语言:
∵四边形ABCD是菱形,
AC=BD,
所以四边形ABCD是正方形.
A
B
C
D
O
归纳
课程讲授
新课推进
已知:如图,在矩形ABCD中,BE平分∠ABC,CE平分∠DCB,BF∥CE,CF∥BE. 求证:四边形BECF是正方形.
思考:通过什么方式证明四边形BECF是正方形?
思路一:先证明四边形BECF是菱形,然后证明四边形BECF中有一个角是直角;
思路二:先证明四边形BECF是矩形,然后证明四边形BECF中有一组邻边相等.
例1
课程讲授
新课推进
【思路二】
证明:∵四边形ABCD是矩形,∴∠ABC=∠DCB=90°.
∵BE平分∠ABC,CE平分∠DCB,∴∠EBC = 45°, ∠ECB = 45°, ∴ ∠EBC=∠ECB=45°,∴EB=EC. ∵BF∥CE,CF ∥BE,
∴∠FBC=∠ECB=45°,∠FCB=∠EBC=45°,
∴∠EBF=∠ECF=∠BEC=90°,∴矩形BECF是正方形.
课程讲授
新课推进
我们知道,任意画一个四边形,以四边的中点为顶点可以组成一个平行四边形.
任意画一个正方形,以四边的中点为顶点可以组成一个怎样的图形呢?先猜一猜,再证明.
A
D
C
B
A1
B1
C1
D1
以正方形四边的中点为顶点,可以组成一个正方形.
证明思路:
利用三角形的中位线证出A1D1=A1B1=C1D1
=C1B1,从而得到四边形A1B1C1D1是矩形,再根据一组邻边相等得出A1B1C1D1是正方形.
课程讲授
新课推进
习题解析
习题1
下列说法正确的是( )
A.一组对边平行另一组对边相等的四边形是平行四边形
B.对角线互相垂直平分的四边形是菱形
C.对角线相等的四边形是矩形
D.对角线互相垂直且相等的四边形是正方形
B
习题解析
习题2
如图,在△ABC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且BE=BF,添加一个条件,仍不能证明四边形BECF为正方形的是( )
A.BC=AC
B.BD=DF
C.AC=BF
D.CF⊥BF
C
习题3
习题解析
如图,在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.
(1)求证:△BED≌△CFD;
证明:∵DE⊥AB,DF⊥AC,
∴∠BED=∠CFD=90°.
∵AB=AC,∴∠B=∠C.
∵D是BC的中点,
∴BD=CD.
∴△BED≌△CFD.
习题解析
(2)若∠A=90°,求证:四边形DFAE是正方形.
解:∵DE⊥AB,DF⊥AC,
∴∠AED=∠AFD=90°.
又∵∠A=90°,∴四边形DFAE为矩形.
由(1)知,△BED≌△CFD,
∴DE=DF.
∴四边形DFAE是正方形.
习题解析
拓展提升
如图,等边三角形AEF的顶点E,F分别在矩形ABCD的边BC,CD上,且∠CEF=45°.
求证:矩形ABCD是正方形.
证明:∵四边形ABCD是矩形,∴∠B=∠D=∠C=90°.
∵△AEF是等边三角形,∴AE=AF,∠AEF=∠AFE=60°.
∵∠CEF=45°,∴∠CFE=∠CEF=45°.
∴∠AFD=∠AEB=180°-45°-60°=75°.
∴△ABE≌△ADF(AAS).∴AB=AD.
∴矩形ABCD是正方形.
课程总结
小结
5种判定方法
三个角是直角
四条边相等
一个角是直角
或对角线相等
一组邻边相等
或对角线垂直
一组邻边相等
或对角线垂直
一个角是直角
或对角线相等
一个角是直角且一组邻边相等
平行四边形、矩形、菱形、正方形的判定小结
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
