人教版八年级上册数学同步练习卷 第十三章 轴对称单元测试(含解析)
文档属性
| 名称 | 人教版八年级上册数学同步练习卷 第十三章 轴对称单元测试(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 762.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-08 09:59:39 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
人教版八年级上册数学同步练习卷
13 本章复习与测试
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图.△ABC中,AB=AC,AB的垂直平分线交AC于P点,若AB=6cm,BC=4cm,△PBC的周长等于( )
A.4cm B.6cm C.8cm D.10cm
2.剪纸是中国的民间艺术,如图是一种剪纸方法的图示(先将纸折叠,然后再剪,展开后即得到图案),下列四幅图案,不能用上述方法剪出的是( )
A.
B.
C.
D.
3.等腰三角形有一个角为80°,顶角等于( )
A.80° B.20° C.80°或20° D.80°或100°
4.如图,中,,的中垂线交于,交于,若,,则的周长为( )
A.16 B.14 C.20 D.18
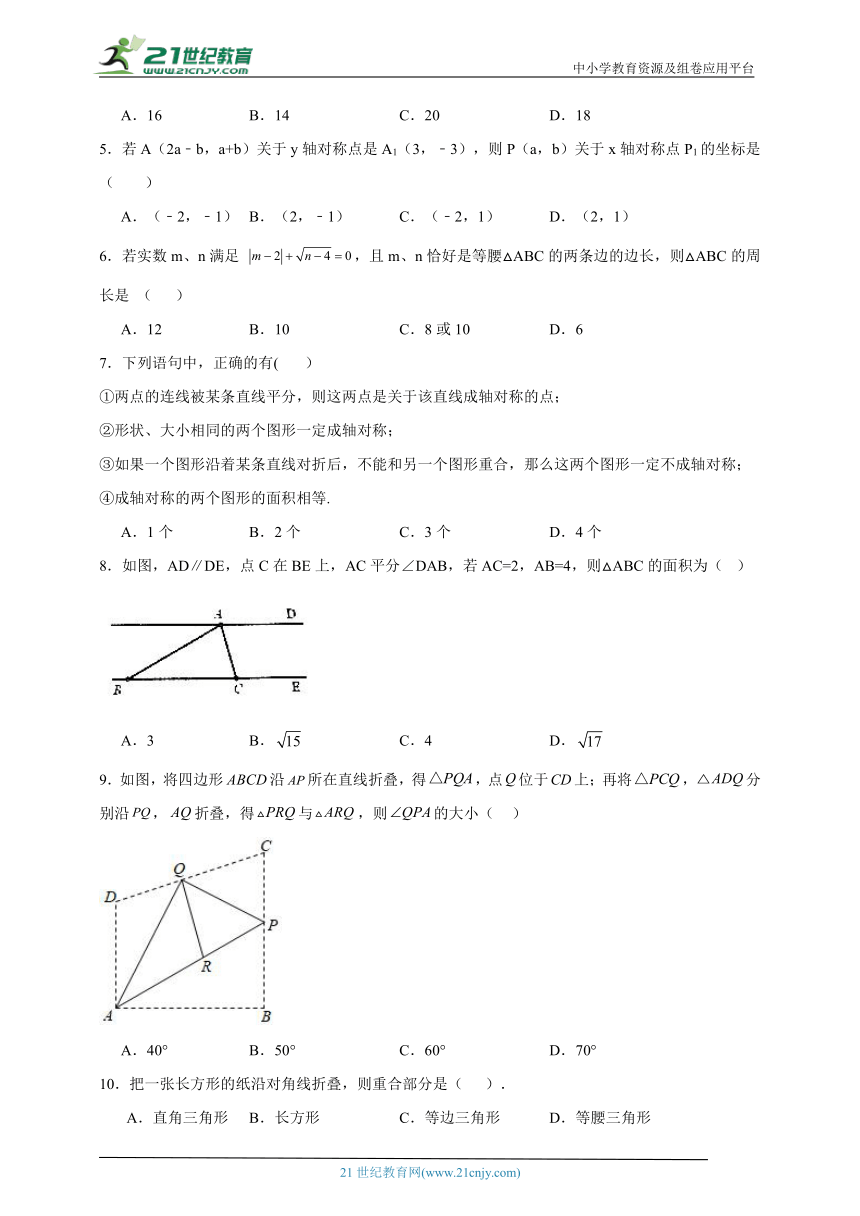
5.若A(2a﹣b,a+b)关于y轴对称点是A1(3,﹣3),则P(a,b)关于x轴对称点P1的坐标是( )
A.(﹣2,﹣1) B.(2,﹣1) C.(﹣2,1) D.(2,1)
6.若实数m、n满足 ,且m、n恰好是等腰△ABC的两条边的边长,则△ABC的周长是 ( )
A.12 B.10 C.8或10 D.6
7.下列语句中,正确的有( )
①两点的连线被某条直线平分,则这两点是关于该直线成轴对称的点;
②形状、大小相同的两个图形一定成轴对称;
③如果一个图形沿着某条直线对折后,不能和另一个图形重合,那么这两个图形一定不成轴对称;
④成轴对称的两个图形的面积相等.
A.1个 B.2个 C.3个 D.4个
8.如图,AD∥DE,点C在BE上,AC平分∠DAB,若AC=2,AB=4,则△ABC的面积为( )
A.3 B. C.4 D.
9.如图,将四边形沿所在直线折叠,得,点位于上;再将,分别沿,折叠,得与,则的大小( )
A.40° B.50° C.60° D.70°
10.把一张长方形的纸沿对角线折叠,则重合部分是( ).
A.直角三角形 B.长方形 C.等边三角形 D.等腰三角形
二、填空题
11.等腰三角形顶角的平分线、底边上的中线、底边上的高 (也称“ ”),它们所在的直线都是等腰三角形的 .
12.关于轴对称的两个图形,沿对称轴折叠后
13.不重合的两点的对称轴是 .
14.等腰三角形一腰上的中线将它的周长分别为8和12两部分,则它的腰长、底边长分别为 .
15.已知:如图,△ABC中,AB=AC,点D为BC的中点,连接AD.
(1)请你写出两个正确结论:① ;② ;
(2)当∠B=60°时,还可以得出正确结论: ;(只需写出一个)
16.△ABC与△ADE关于直线MN成轴对称,连接CE交MN于点F,∠BAC=90°,∠DAC=30°,CE=6,则∠CAE的度数为 ,点E到直线MN的距离为 .
17.如图,,平行线间有一点C,使得平分,平分,连接交于点E.若E为的中点,且,则等于 ;
三、解答题
18.有一些整数你无论从左往右看,还是从右往左看,数字都是完全一样,例如:22,131,1991,123321,…,像这样的数,我们称为“回文数”.回文数实际上是由左右排列对称的自然数构成的,有趣的是,当你遇到一个普通的数(两位以上),经过一定的计算,可以变成“回文数”.办法很简单:只要将这个数加上它的逆序数就可以了,若一次不成功,反复进行下去,一定能得到一个回文数,比如:①132+231=363;②7299+9927=17226,17226+62271=79497.
(1)你能用上述方法,将下列各数“变”成回文数吗?
①237;
②362.
(2)请写出一个四位数,并用上述方法将它变成回文数.
19.在△ABC中,AB=AC≠BC,点D和点A在直线BC的同侧,BD=BC,∠BAC=α,∠DBC=β,且α+β=120°,连接AD,求∠ADB的度数.(不必解答)
(1)小聪先从特殊问题开始研究,当α=90°,β=30°时,利用轴对称知识,以AB为对称轴构造△ABD的轴对称图形△ABD′,连接CD′(如图2),然后利用α=90°,β=30°以及等边三角形等相关知识便可解决这个问题.
请结合小聪研究问题的过程和思路,在这种特殊情况下填空:△D′BC的形状是 三角形;∠ADB的度数为 .
(2)在原问题中,当∠DBC<∠ABC(如图1)时,请计算∠ADB的度数;
(3)在原问题中,过点A作直线AE⊥BD,交直线BD于E,其他条件不变若BC=7,AD=2.请直接写出线段BE的长为 .
20.如图,在中,,,,在中,,,,
、两点在上,、两边分别与边交于点、.固定不动,从点与点
B重合的位置出发,沿边以每秒个单位的速度向点运动;同时点从点出发,在折线上
以每秒个单位的速度向点运动.当点到达点时,和点同时停止运动.设运动时间为(秒).
(1)当时,__________,__________.
(2)当为何值时,为等腰三角形?请说明理由.
(3)当为何值时,点与点重合?写出计算过程.
参考答案:
1.D
【详解】AB=AC,AB的垂直平分线交AC于P点,所以AP=BP=BC=4,PC=2,所以△PBC周长是10.故选D.
2.A
【详解】由题意知,剪出的图形一定是轴对称图形,四个选项中,只有A不是轴对称图形,
所以A不能用上述方法剪出
3.C
【详解】分析:本题只要根据等腰三角形的性质分两种情况进行讨论即可得出答案.
详解:当80°为顶角时,则顶角为80°;当80°为底角时,则顶角为180°-80°×2=20°,
4.A
【详解】由题可知,DE是AB的垂直平分线,
∴,
∵,
∴,
又∵,
∴的周长.
5.C
【详解】解:由A(2a-b,a+b)关于y轴对称点是A1(3,-3),
得,
解得,
∴P(-2,-1).
P(-2,-1)关于x轴对称点P1的坐标是(-2,1),
6.B
【详解】由题意得:m-2=0,n-4=0,∴m=2,n=4,
又∵m、n恰好是等腰△ABC的两条边的边长,
①若腰为2,底为4,此时不能构成三角形,舍去,
②若腰为4,底为2,则周长为:4+4+2=10,
7.A
【详解】①两点的连线被某条直线平分,则这两点是关于该直线成轴对称的点;错误;
②形状、大小相同的两个图形一定成轴对称;错误;
③如果一个图形沿着某条直线对折后,不能和另一个图形重合,那么这两个图形一定不成轴对称;错误,关键是看这条直线是否为对称轴了;
④成轴对称的两个图形的面积相等.正确,成轴对称的两个图形一定是全等的.故面积相等.
8.B
【详解】试题解析:过点作于
AC平分∠DAB,
AD∥DE,
是等腰三角形,
9.C
【详解】解:由折叠可得∠BPA=∠QPA=∠QPC,
∵∠BPA+∠QPA+∠QPC=180°,
∴3∠QPA =180°,
∴∠QPA =60°,
10.D
【详解】折叠后的图形如图所示,
根据轴对称的性质可得AF=CD=AB,∠F=∠D=90°
又∠FHA=∠DHC,
∴△FAH≌△DCH(AAS)
∴CH=AH,即重合部分为等腰三角形.
11. 重合, 三线合一, 对称轴
【详解】等腰三角形顶角的平分线、底边上的中线、底边上的高重合(也称“三线合一”),它们所在的直线都是等腰三角形的对称轴.
12.重合
【详解】关于轴对称的两个图形,沿对称轴折叠后重合.
13.连结这两点所成线段的垂直平分线和两点所在的直线
【详解】∵两点之间线段最短
∴连结已知不重合两点,得一线段
∴原题变成求一条线段的对称轴
而线段的对称轴是它的垂直平分线
∴不重合的两点的对称轴是连结这两点所成线段的垂直平分线.
14.8,8,4或
【详解】设底边长a,腰长b,则有
(1)a+=8,
b+=12,
解得:a=4,b=8,
即腰长、底边长分别为:8,8,4;
(2)a+=12,
b+=8,
得a= ,b=,
即腰长、底边长分别为:,,,
综上,腰长、底边长分别为:8,8,4或,,,
15. AD⊥BC △ABD≌△ACD △ABC是等边三角形
【详解】:(1)根据三线合一的性质及全等三角形的判定,写出两个结论即可;
(2)根据等边三角形的判定定理可得△ABC是等边三角形.
详解:(1)①AD⊥BC;②△ABD≌△ACD;
故答案为AD⊥BC,△ABD≌△ACD.
(2)∵AB=AC,∠B=60°,∴△ABC是等边三角形.
16. 60° 3
【详解】由题意可得:∠DAE=∠BAC=90°,CF=EF=CE,
∴∠CAE=∠DAE-∠DAC=90°-30°=60°,
EF=×6=3,
17./50度
【详解】解:如图,过点C作交于点N,
,
为的中点,
,
,
,
平分,
,
,
,
,
平分,
,
,
,
,
平分,
,
,
,
,
18.(1)①969;②625;(2)2662
【详解】:(1)①,要将237“变”成回文数,可用237+732计算.同理,还可完成②;
(2)根据回文数的定义写出一个四位数,并将其“变”成回文数即可,答案不唯一.
试题解析:(1)①237+732=969,②362+263=625,
(2)1151+1511=2662.
19.(1)①△D′BC是等边三角形,②∠ADB=30°(2)∠ADB=30°;(3)7+或7﹣
【详解】(1)①如图2中,作∠ABD′=∠ABD,BD′=BD,连接CD′,AD′,
∵AB=AC,∠BAC=90°,
∴∠ABC=45°,
∵∠DBC=30°,
∴∠ABD=∠ABC﹣∠DBC=15°,
在△ABD和△ABD′中,
∴△ABD≌△ABD′,
∴∠ABD=∠ABD′=15°,∠ADB=∠AD′B,
∴∠D′BC=∠ABD′+∠ABC=60°,
∵BD=BD′,BD=BC,
∴BD′=BC,
∴△D′BC是等边三角形,
②∵△D′BC是等边三角形,
∴D′B=D′C,∠BD′C=60°,
在△AD′B和△AD′C中,
∴△AD′B≌△AD′C,
∴∠AD′B=∠AD′C,
∴∠AD′B=∠BD′C=30°,
∴∠ADB=30°.
(2)∵∠DBC<∠ABC,
∴60°<α≤120°,
如图3中,作∠ABD′=∠ABD,BD′=BD,连接CD′,AD′,
∵AB=AC,
∴∠ABC=∠ACB,
∵∠BAC=α,
∴∠ABC=(180°﹣α)=90°﹣α,
∴∠ABD=∠ABC﹣∠DBC=90°﹣α﹣β,
同(1)①可证△ABD≌△ABD′,
∴∠ABD=∠ABD′=90°﹣α﹣β,BD=BD′,∠ADB=∠AD′B
∴∠D′BC=∠ABD′+∠ABC=90°﹣α﹣β+90°﹣α=180°﹣(α+β),
∵α+β=120°,
∴∠D′BC=60°,
由(1)②可知,△AD′B≌△AD′C,
∴∠AD′B=∠AD′C,
∴∠AD′B=∠BD′C=30°,
∴∠ADB=30°.
(3)第①情况:当60°<α<120°时,如图3﹣1,
由(2)知,∠ADB=30°,
作AE⊥BD,
在Rt△ADE中,∠ADB=30°,AD=2,
∴DE=,
∵△BCD'是等边三角形,
∴BD'=BC=7,
∴BD=BD'=7,
∴BE=BD﹣DE=7﹣;
第②情况:当0°<α<60°时,
如图4中,作∠ABD′=∠ABD,BD′=BD,连接CD′,AD′.
同理可得:∠ABC=(180°﹣α)=90°﹣α,
∴∠ABD=∠DBC﹣∠ABC=β﹣(90°﹣α),
同(1)①可证△ABD≌△ABD′,
∴∠ABD=∠ABD′=β﹣(90°﹣α),BD=BD′,∠ADB=∠AD′B,
∴∠D′BC=∠ABC﹣∠ABD′=90°﹣α﹣[β﹣(90°﹣α)]=180°﹣(α+β),
∴D′B=D′C,∠BD′C=60°.
同(1)②可证△AD′B≌△AD′C,
∴∠AD′B=∠AD′C,
∵∠AD′B+∠AD′C+∠BD′C=360°,
∴∠ADB=∠AD′B=150°,
在Rt△ADE中,∠ADE=30°,AD=2,
∴DE=,
∴BE=BD+DE=7+,
20.(),;
()时,为等腰三角形,明理由见解析;
()时,点与点重合,计算过程见解析.
【详解】分析:(1)当t=2,得到BF=2,PF=4,根据BF:BC=HF:AC,即可求出HF,从而得到PH;BE=8,利用Rt△BEG∽Rt△BAC,可求出EG,得到DG;
(2)根据题意得到PD=PE,则BF=t,PF=2t,DF=8,得到PD=DF-PF=8-2t.在Rt△PEF中,利用勾股定理得到4t +36=(8-2t) ,解得t= .(3)设当△DEF和点P运动的时间是t时,点P与点G重合,此时点P一定在DE边上,DP=DG.根据正切的定义得到tanB=tanD=,则FH=t,DH=,得到DG=,而DP+DF=2t,于是有2t-8=,即可解得t的值.
本题解析:
()∵,,∴,∴,,
∴,∴,即,,,∴,
∴当时,∵,又∵,
∴,∴,
∵,∴,∴,
,,
,∴当时,.
()只有点在边上运动时,才能成为等腰三角形,且.
∵,,,
∴,
在中,,
,
∵ ∴,
即,
∴,
∴当时,为等腰三角形.
(3)设当和点运动的时间是时,点与点重合,
此时,点在上,,
由已知可得:,,
∴,
∵,
∴,
∴,
∴,
,
,
∵,
∴,
∵,
∴,
∵,则此时点在上,
当时,点与点重合.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
人教版八年级上册数学同步练习卷
13 本章复习与测试
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图.△ABC中,AB=AC,AB的垂直平分线交AC于P点,若AB=6cm,BC=4cm,△PBC的周长等于( )
A.4cm B.6cm C.8cm D.10cm
2.剪纸是中国的民间艺术,如图是一种剪纸方法的图示(先将纸折叠,然后再剪,展开后即得到图案),下列四幅图案,不能用上述方法剪出的是( )
A.
B.
C.
D.
3.等腰三角形有一个角为80°,顶角等于( )
A.80° B.20° C.80°或20° D.80°或100°
4.如图,中,,的中垂线交于,交于,若,,则的周长为( )
A.16 B.14 C.20 D.18
5.若A(2a﹣b,a+b)关于y轴对称点是A1(3,﹣3),则P(a,b)关于x轴对称点P1的坐标是( )
A.(﹣2,﹣1) B.(2,﹣1) C.(﹣2,1) D.(2,1)
6.若实数m、n满足 ,且m、n恰好是等腰△ABC的两条边的边长,则△ABC的周长是 ( )
A.12 B.10 C.8或10 D.6
7.下列语句中,正确的有( )
①两点的连线被某条直线平分,则这两点是关于该直线成轴对称的点;
②形状、大小相同的两个图形一定成轴对称;
③如果一个图形沿着某条直线对折后,不能和另一个图形重合,那么这两个图形一定不成轴对称;
④成轴对称的两个图形的面积相等.
A.1个 B.2个 C.3个 D.4个
8.如图,AD∥DE,点C在BE上,AC平分∠DAB,若AC=2,AB=4,则△ABC的面积为( )
A.3 B. C.4 D.
9.如图,将四边形沿所在直线折叠,得,点位于上;再将,分别沿,折叠,得与,则的大小( )
A.40° B.50° C.60° D.70°
10.把一张长方形的纸沿对角线折叠,则重合部分是( ).
A.直角三角形 B.长方形 C.等边三角形 D.等腰三角形
二、填空题
11.等腰三角形顶角的平分线、底边上的中线、底边上的高 (也称“ ”),它们所在的直线都是等腰三角形的 .
12.关于轴对称的两个图形,沿对称轴折叠后
13.不重合的两点的对称轴是 .
14.等腰三角形一腰上的中线将它的周长分别为8和12两部分,则它的腰长、底边长分别为 .
15.已知:如图,△ABC中,AB=AC,点D为BC的中点,连接AD.
(1)请你写出两个正确结论:① ;② ;
(2)当∠B=60°时,还可以得出正确结论: ;(只需写出一个)
16.△ABC与△ADE关于直线MN成轴对称,连接CE交MN于点F,∠BAC=90°,∠DAC=30°,CE=6,则∠CAE的度数为 ,点E到直线MN的距离为 .
17.如图,,平行线间有一点C,使得平分,平分,连接交于点E.若E为的中点,且,则等于 ;
三、解答题
18.有一些整数你无论从左往右看,还是从右往左看,数字都是完全一样,例如:22,131,1991,123321,…,像这样的数,我们称为“回文数”.回文数实际上是由左右排列对称的自然数构成的,有趣的是,当你遇到一个普通的数(两位以上),经过一定的计算,可以变成“回文数”.办法很简单:只要将这个数加上它的逆序数就可以了,若一次不成功,反复进行下去,一定能得到一个回文数,比如:①132+231=363;②7299+9927=17226,17226+62271=79497.
(1)你能用上述方法,将下列各数“变”成回文数吗?
①237;
②362.
(2)请写出一个四位数,并用上述方法将它变成回文数.
19.在△ABC中,AB=AC≠BC,点D和点A在直线BC的同侧,BD=BC,∠BAC=α,∠DBC=β,且α+β=120°,连接AD,求∠ADB的度数.(不必解答)
(1)小聪先从特殊问题开始研究,当α=90°,β=30°时,利用轴对称知识,以AB为对称轴构造△ABD的轴对称图形△ABD′,连接CD′(如图2),然后利用α=90°,β=30°以及等边三角形等相关知识便可解决这个问题.
请结合小聪研究问题的过程和思路,在这种特殊情况下填空:△D′BC的形状是 三角形;∠ADB的度数为 .
(2)在原问题中,当∠DBC<∠ABC(如图1)时,请计算∠ADB的度数;
(3)在原问题中,过点A作直线AE⊥BD,交直线BD于E,其他条件不变若BC=7,AD=2.请直接写出线段BE的长为 .
20.如图,在中,,,,在中,,,,
、两点在上,、两边分别与边交于点、.固定不动,从点与点
B重合的位置出发,沿边以每秒个单位的速度向点运动;同时点从点出发,在折线上
以每秒个单位的速度向点运动.当点到达点时,和点同时停止运动.设运动时间为(秒).
(1)当时,__________,__________.
(2)当为何值时,为等腰三角形?请说明理由.
(3)当为何值时,点与点重合?写出计算过程.
参考答案:
1.D
【详解】AB=AC,AB的垂直平分线交AC于P点,所以AP=BP=BC=4,PC=2,所以△PBC周长是10.故选D.
2.A
【详解】由题意知,剪出的图形一定是轴对称图形,四个选项中,只有A不是轴对称图形,
所以A不能用上述方法剪出
3.C
【详解】分析:本题只要根据等腰三角形的性质分两种情况进行讨论即可得出答案.
详解:当80°为顶角时,则顶角为80°;当80°为底角时,则顶角为180°-80°×2=20°,
4.A
【详解】由题可知,DE是AB的垂直平分线,
∴,
∵,
∴,
又∵,
∴的周长.
5.C
【详解】解:由A(2a-b,a+b)关于y轴对称点是A1(3,-3),
得,
解得,
∴P(-2,-1).
P(-2,-1)关于x轴对称点P1的坐标是(-2,1),
6.B
【详解】由题意得:m-2=0,n-4=0,∴m=2,n=4,
又∵m、n恰好是等腰△ABC的两条边的边长,
①若腰为2,底为4,此时不能构成三角形,舍去,
②若腰为4,底为2,则周长为:4+4+2=10,
7.A
【详解】①两点的连线被某条直线平分,则这两点是关于该直线成轴对称的点;错误;
②形状、大小相同的两个图形一定成轴对称;错误;
③如果一个图形沿着某条直线对折后,不能和另一个图形重合,那么这两个图形一定不成轴对称;错误,关键是看这条直线是否为对称轴了;
④成轴对称的两个图形的面积相等.正确,成轴对称的两个图形一定是全等的.故面积相等.
8.B
【详解】试题解析:过点作于
AC平分∠DAB,
AD∥DE,
是等腰三角形,
9.C
【详解】解:由折叠可得∠BPA=∠QPA=∠QPC,
∵∠BPA+∠QPA+∠QPC=180°,
∴3∠QPA =180°,
∴∠QPA =60°,
10.D
【详解】折叠后的图形如图所示,
根据轴对称的性质可得AF=CD=AB,∠F=∠D=90°
又∠FHA=∠DHC,
∴△FAH≌△DCH(AAS)
∴CH=AH,即重合部分为等腰三角形.
11. 重合, 三线合一, 对称轴
【详解】等腰三角形顶角的平分线、底边上的中线、底边上的高重合(也称“三线合一”),它们所在的直线都是等腰三角形的对称轴.
12.重合
【详解】关于轴对称的两个图形,沿对称轴折叠后重合.
13.连结这两点所成线段的垂直平分线和两点所在的直线
【详解】∵两点之间线段最短
∴连结已知不重合两点,得一线段
∴原题变成求一条线段的对称轴
而线段的对称轴是它的垂直平分线
∴不重合的两点的对称轴是连结这两点所成线段的垂直平分线.
14.8,8,4或
【详解】设底边长a,腰长b,则有
(1)a+=8,
b+=12,
解得:a=4,b=8,
即腰长、底边长分别为:8,8,4;
(2)a+=12,
b+=8,
得a= ,b=,
即腰长、底边长分别为:,,,
综上,腰长、底边长分别为:8,8,4或,,,
15. AD⊥BC △ABD≌△ACD △ABC是等边三角形
【详解】:(1)根据三线合一的性质及全等三角形的判定,写出两个结论即可;
(2)根据等边三角形的判定定理可得△ABC是等边三角形.
详解:(1)①AD⊥BC;②△ABD≌△ACD;
故答案为AD⊥BC,△ABD≌△ACD.
(2)∵AB=AC,∠B=60°,∴△ABC是等边三角形.
16. 60° 3
【详解】由题意可得:∠DAE=∠BAC=90°,CF=EF=CE,
∴∠CAE=∠DAE-∠DAC=90°-30°=60°,
EF=×6=3,
17./50度
【详解】解:如图,过点C作交于点N,
,
为的中点,
,
,
,
平分,
,
,
,
,
平分,
,
,
,
,
平分,
,
,
,
,
18.(1)①969;②625;(2)2662
【详解】:(1)①,要将237“变”成回文数,可用237+732计算.同理,还可完成②;
(2)根据回文数的定义写出一个四位数,并将其“变”成回文数即可,答案不唯一.
试题解析:(1)①237+732=969,②362+263=625,
(2)1151+1511=2662.
19.(1)①△D′BC是等边三角形,②∠ADB=30°(2)∠ADB=30°;(3)7+或7﹣
【详解】(1)①如图2中,作∠ABD′=∠ABD,BD′=BD,连接CD′,AD′,
∵AB=AC,∠BAC=90°,
∴∠ABC=45°,
∵∠DBC=30°,
∴∠ABD=∠ABC﹣∠DBC=15°,
在△ABD和△ABD′中,
∴△ABD≌△ABD′,
∴∠ABD=∠ABD′=15°,∠ADB=∠AD′B,
∴∠D′BC=∠ABD′+∠ABC=60°,
∵BD=BD′,BD=BC,
∴BD′=BC,
∴△D′BC是等边三角形,
②∵△D′BC是等边三角形,
∴D′B=D′C,∠BD′C=60°,
在△AD′B和△AD′C中,
∴△AD′B≌△AD′C,
∴∠AD′B=∠AD′C,
∴∠AD′B=∠BD′C=30°,
∴∠ADB=30°.
(2)∵∠DBC<∠ABC,
∴60°<α≤120°,
如图3中,作∠ABD′=∠ABD,BD′=BD,连接CD′,AD′,
∵AB=AC,
∴∠ABC=∠ACB,
∵∠BAC=α,
∴∠ABC=(180°﹣α)=90°﹣α,
∴∠ABD=∠ABC﹣∠DBC=90°﹣α﹣β,
同(1)①可证△ABD≌△ABD′,
∴∠ABD=∠ABD′=90°﹣α﹣β,BD=BD′,∠ADB=∠AD′B
∴∠D′BC=∠ABD′+∠ABC=90°﹣α﹣β+90°﹣α=180°﹣(α+β),
∵α+β=120°,
∴∠D′BC=60°,
由(1)②可知,△AD′B≌△AD′C,
∴∠AD′B=∠AD′C,
∴∠AD′B=∠BD′C=30°,
∴∠ADB=30°.
(3)第①情况:当60°<α<120°时,如图3﹣1,
由(2)知,∠ADB=30°,
作AE⊥BD,
在Rt△ADE中,∠ADB=30°,AD=2,
∴DE=,
∵△BCD'是等边三角形,
∴BD'=BC=7,
∴BD=BD'=7,
∴BE=BD﹣DE=7﹣;
第②情况:当0°<α<60°时,
如图4中,作∠ABD′=∠ABD,BD′=BD,连接CD′,AD′.
同理可得:∠ABC=(180°﹣α)=90°﹣α,
∴∠ABD=∠DBC﹣∠ABC=β﹣(90°﹣α),
同(1)①可证△ABD≌△ABD′,
∴∠ABD=∠ABD′=β﹣(90°﹣α),BD=BD′,∠ADB=∠AD′B,
∴∠D′BC=∠ABC﹣∠ABD′=90°﹣α﹣[β﹣(90°﹣α)]=180°﹣(α+β),
∴D′B=D′C,∠BD′C=60°.
同(1)②可证△AD′B≌△AD′C,
∴∠AD′B=∠AD′C,
∵∠AD′B+∠AD′C+∠BD′C=360°,
∴∠ADB=∠AD′B=150°,
在Rt△ADE中,∠ADE=30°,AD=2,
∴DE=,
∴BE=BD+DE=7+,
20.(),;
()时,为等腰三角形,明理由见解析;
()时,点与点重合,计算过程见解析.
【详解】分析:(1)当t=2,得到BF=2,PF=4,根据BF:BC=HF:AC,即可求出HF,从而得到PH;BE=8,利用Rt△BEG∽Rt△BAC,可求出EG,得到DG;
(2)根据题意得到PD=PE,则BF=t,PF=2t,DF=8,得到PD=DF-PF=8-2t.在Rt△PEF中,利用勾股定理得到4t +36=(8-2t) ,解得t= .(3)设当△DEF和点P运动的时间是t时,点P与点G重合,此时点P一定在DE边上,DP=DG.根据正切的定义得到tanB=tanD=,则FH=t,DH=,得到DG=,而DP+DF=2t,于是有2t-8=,即可解得t的值.
本题解析:
()∵,,∴,∴,,
∴,∴,即,,,∴,
∴当时,∵,又∵,
∴,∴,
∵,∴,∴,
,,
,∴当时,.
()只有点在边上运动时,才能成为等腰三角形,且.
∵,,,
∴,
在中,,
,
∵ ∴,
即,
∴,
∴当时,为等腰三角形.
(3)设当和点运动的时间是时,点与点重合,
此时,点在上,,
由已知可得:,,
∴,
∵,
∴,
∴,
∴,
,
,
∵,
∴,
∵,
∴,
∵,则此时点在上,
当时,点与点重合.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
