人教版八年级上册数学同步练习卷 13.1.1 轴对称(含解析)
文档属性
| 名称 | 人教版八年级上册数学同步练习卷 13.1.1 轴对称(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-08 10:31:02 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
人教版八年级上册数学同步练习卷
13.1.1 轴对称
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图1,将长方形ABCD沿CE(点E在AB上,不与点A,B重合)折叠,点B落在点处,连接,,设,.变化长方形的大小如图2所示,若的值增大了,且保持不变,则的值( )
A.增大了 B.减小了 C.增大了 D.减小了
2.下列标志中,可以看作是轴对称图形的是( )
A. B. C. D.
3.以下会徽是轴对称图形的是( ).
A. B.
C. D.
4.下列国产车标属于轴对称图形的是( )
A. B. C. D.
5.下列常见平面图形不是轴对称图形的是( )
A. B. C. D.
6.下列说法中,正确的是( )
A.等腰直角三角形不是轴对称图形 B.角的平分线是角的对称轴
C.线段的垂直平分线是线段的一条对称轴 D.轴对称图形是由两个图形组成的
7.在下列图形中,为轴对称图形的是( )
A. B. C. D.
8.下列图形中对称轴最多的是( )
A. B.
C. D.
9.下列城市的地铁图标中,不是轴对称图形的是( )
A. B. C. D.
10.如图是同学们生活中常见的品牌,其中,不是轴对称图形的是( )
A. B. C. D.
11.如图,将四边形纸片ABCD沿MN折叠,点A、D分别落在点A1、D1处.若∠1+∠2=130°,则∠B+∠C=( )
A.115° B.130° C.135 ° D.150°
12.如图,在中,点,分别是,上两点,将沿折叠,使点落在点处,若,,则的度数是( )
A. B. C. D.
二、填空题
13.如图,点P是内一点,点Q,R分别是点P关于,的对称点,与交于点M,与交于点N.若已知的周长为8cm,则 .
14.如图,将一张长方形纸片折叠成如图所示的形状,若,则的度数为
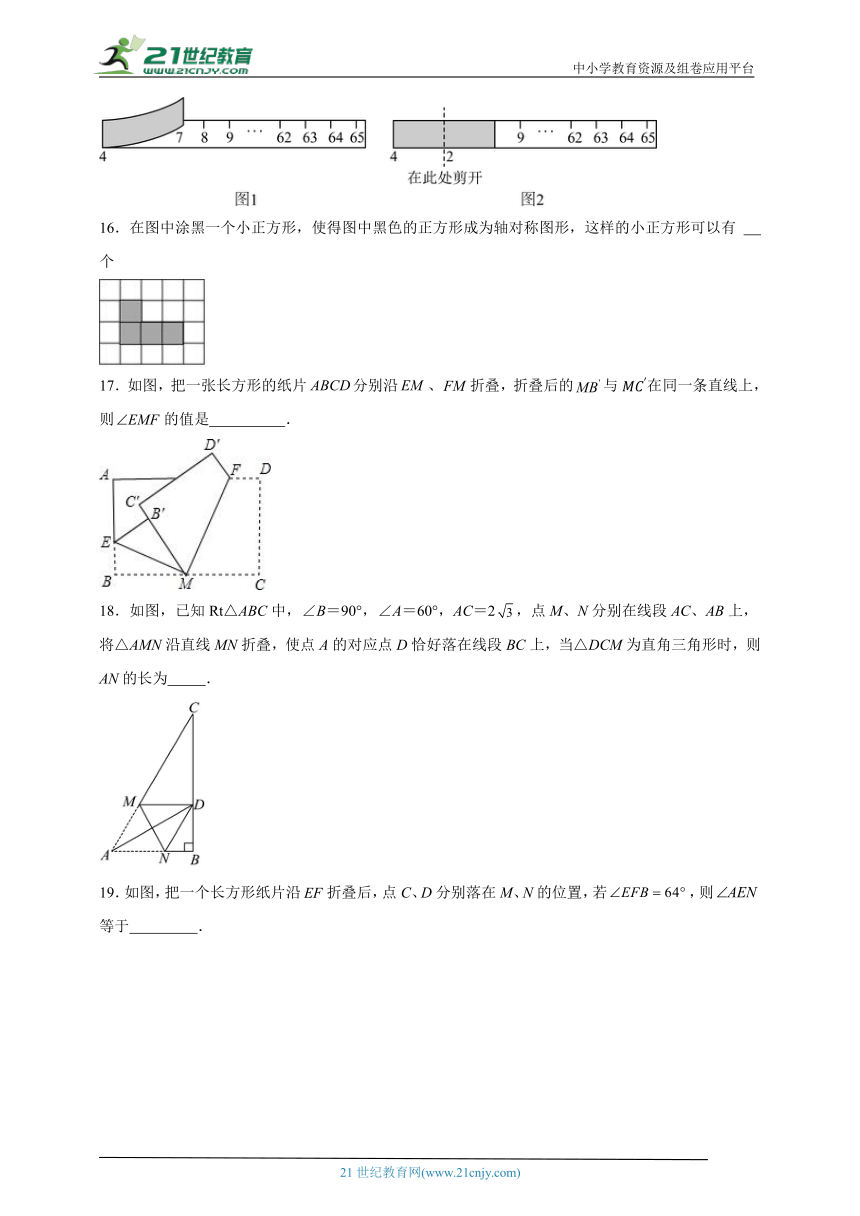
15.有一条长的卷尺.若在刻度4处折叠(如图1所示),折叠后,在重叠部分刻度为2和6的位置用剪刀剪开(如图2所示),可将该卷尺剪成三段.若小桐将该卷尺在刻度30处折叠,并在整数刻度处剪开,她剪下的三段卷尺中的两段,其中一段是另一段的3倍,则剪开处的刻度可以是 .(写出其中一种即可)
16.在图中涂黑一个小正方形,使得图中黑色的正方形成为轴对称图形,这样的小正方形可以有 个
17.如图,把一张长方形的纸片分别沿、折叠,折叠后的与在同一条直线上,则的值是 .
18.如图,已知Rt△ABC中,∠B=90°,∠A=60°,AC=2,点M、N分别在线段AC、AB上,将△AMN沿直线MN折叠,使点A的对应点D恰好落在线段BC上,当△DCM为直角三角形时,则AN的长为 .
19.如图,把一个长方形纸片沿折叠后,点C、D分别落在M、N的位置,若,则等于 .
20.若点,关于轴对称,则的值为 .
三、解答题
21.(1)将一张长方形纸片按如图1所示的方式折叠,、为折痕,求的度数;
(2)将一张长方形纸片按如图2所示的方式折叠,、为折痕,若,求的度数;
(3)将一张长方形纸片按如图3所示的方式折叠,、为折痕,若,请直接写出的度数(用含的式子表示)
22.如图,点P在四边形的内部,且点P与点M关于对称,交于点G,点P与点N关于对称,交于点H,分别交于点.
(1)连接,若求的周长;
(2)若,求的度数.
23.如图①,将一张长方形纸片沿EF对折,使AB落在的位置;
(1)若∠1的度数为a,试求∠2的度数(用含a的代数式表示);
(2)如图②,再将纸片沿GH对折,使得CD落在的位置.
①若,∠1的度数为a,试求∠3的度数(用含a的代数式表示):
②若,∠3的度数比∠1的度数大20°,试计算∠1的度数.
24.小明同学学习了轴对称后,忽然想起了做过的一道题:如图,有一组数排列成方阵,试计算这组数的和.小明想方阵就像正方形,正方形是轴对称图形,能不能用轴对称的思想来解决方阵的计算问题呢?小明试了试,竞得到非常巧妙的方法,你也能试试看吗?
参考答案:
1.C
【详解】解:∵将长方形ABCD沿CE(点E在AB上,不与点A,B重合)折叠,点B落在点处,
∴,
∵,
∴,
∵,
∴,
∵的值增大了,
∴,
∴的值增大了,
2.C
【详解】解:A、B、D选项中的汉字都不能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形;C选项中的汉字能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形;
3.A
【详解】解:A. 是轴对称图形;
B.不是轴对称图形;
C.不是轴对称图形;
D.不是轴对称图形,
4.A
【详解】A、是轴对称图形,故正确;
B、不是轴对称图形,故错误;
C、不是轴对称图形,故错误;
D、不是轴对称图形,故错误.
5.C
【详解】A.等腰三角形是轴对称图形,故A不符合题意;
B.正方形是轴对称图形,故B不符合题意;
C.平行四边形不是轴对称图形,故C符合题意;
D.圆形是轴对称图形,故D不符合题意.
6.C
【详解】解:A、等腰直角三角形是轴对称图形,原说法错误,不符合题意.
B、角的平分线所在的直线是角的对称轴,原说法错误,不符合题意.
C、线段的垂直平分线是线段的一条对称轴,正确,符合题意.
D、轴对称图形是由一个图形组成的,原说法错误,不符合题意.
7.C
【详解】如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形(axially symmetric figure),这条直线叫做对称轴(axis of symmetric);这时,我们也说这个图形 关于这条直线的轴对称.C图符合
8.A
【详解】解:圆有无数条对称轴,正六边形有条对称轴,正方形有4条对称轴,等边三角形有3条对称轴,
9.D
【详解】解:A.是轴对称图形,故本选项不合题意;
B.是轴对称图形,故本选项不合题意;
C.是轴对称图形,故本选项不合题意;
D.不是轴对称图形,故本选项符合题意;
10.B
【详解】解:A、是轴对称图形,不符合题意;
B、不是轴对称图形,符合题意;
C、是轴对称图形,不符合题意;
D、是轴对称图形,不符合题意;
11.A
【详解】解:∵∠1+∠2=130°,
∴∠AMN+∠DNM=,
∵∠A+∠D+∠AMN+∠DNM=360°,∠A+∠D+∠B+∠C=360°,
∴∠B+∠C=∠AMN+∠DNM=115°,
12.C
【详解】解:由折叠可得:,,
,
,
,
,
,
,
.
13.8cm
【详解】解:点,分别是点关于射线,的对称点,
,,
的周长,
的周长为,
.
14./40度
【详解】解:∵四边形是长方形,
∴,,
∴
由折叠的性质可得出:,,
∴,,
∴,
∴,
又∵,
∴,
15.12和48或25和35或9和51(写出其中任意一组即可)
【详解】解:设在重叠部分刻度为和的位置用剪刀剪开,则剪下的三段卷尺的长分别为,,
①取 ,,则或,
解得:(不符合题意,舍去)或,
,
剪开处的刻度可以是12和48;
②取,,则或,
解得:(不符合题意,舍去)或(不符合题意,舍去);
③取,,则或,
解得:,,
当时,;
当时,,
剪开处的刻度可以是9和51,25和35.
16.3
【详解】如图,涂黑一个小正方形,使得图中黑色的正方形成为轴对称图形,这样的小正方形共有3个.
故答案为:3.
17.90°
【详解】解:∵△B'ME是△BME沿直线EM翻折变换而成,四边形CMFD'是四边形CMFD翻折变换而成,
∴∠BME=∠B'ME=∠BMB',∠CMF=∠C'MF=∠CMC',
∵∠BMB'+∠CMC'=180°,
∴∠B'ME+∠C'MF=90°,
∴∠EMF=90°.
18.或4﹣6.
【详解】解:分两种情况:
①如图,当∠CDM=90°时,△CDM是直角三角形,
∵在Rt△ABC中,∠B=90°,∠A=60°,AC=2,
∴∠C=30°,AB=AC=,
由折叠可得,∠MDN=∠A=60°,
∴∠BDN=30°,
∴BN=DN=AN,
∴BN=AB=,
∴AN=2BN=;
②如图,当∠CMD=90°时,△CDM是直角三角形,
由题意可得,∠CDM=60°,∠A=∠MDN=60°,
∴∠BDN=60°,∠BND=30°,
∴BD=DN=AN,BN=BD,
又∵AB=,
∴2BD+BD=,
解得:BD=2﹣3,
∴AN=2BD=4﹣6;
19.52°/52度
【详解】解:∵∠EFB=64°,ADCB,
∴∠DEF=64°,
由折叠可得∠NEF=∠DEF=64°,
∴∠AEN=180°-64°-64°=52°,
20.
【详解】解: 点,关于轴对称,
21.(1);(2);(3).
【详解】解:(1)由折叠的性质知,,
∴,,
∴;
(2)由折叠的性质知,,
∴,,
∵,
∴,
∴;
(3)由折叠的性质知,,
∴,,
∵,
∴,则,
∴.
22.(1)12cm (2)134°
【详解】(1)如图,∵点P与点M关于对称,
∴,
∵点P与点N关于对称,
∴,
∵,
∴的周长为.
(2)解:∵点P与点M 关于对称,
∴,
即,
∵点P 与点N 关于 对称,
∴,
即,
∵,,
∴,
∵,
∴.
23.(1);(2)①;②50°
【详解】解:(1)如图,
由题意可知,A′E//B′F,
∴∠4=∠1=α,
∵AD//BC,
∴∠4=∠B′FC=α,
由折叠的性质可知,∠2=∠BFE,
∵∠BFE+∠2+∠B′FC=180°,
∴∠2=×(180°-α)=;
(2)①由(1)知,∠BFE=90°-α,
∵EF//C′G,
∴∠BFE=∠C′GB=,
再由折叠的性质可知,∠3+∠HGC=180°-,
∴∠3=∠HGC=;
②由(1)知,∠BFE=∠EFB′=90°-∠1,
由B′F⊥C′G可知,∠B′FC+∠FGC′=90°,
∴180°-2×(90°-∠1)+(180°-2∠3)=90°,
即∠1+180°-2∠3=90°,
∵∠3=∠1+20°,
∴∠1=50°.
24.【详解】解:从方阵中的数看出,一条对角线上的数都是5,把这条对角线当作轴,把正方形翻折一下,对称位置的两数之和都是10,
所以这样方阵中数的和=10×(1+2+3+4)+5×5=10×10+25=100+25=125.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
人教版八年级上册数学同步练习卷
13.1.1 轴对称
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图1,将长方形ABCD沿CE(点E在AB上,不与点A,B重合)折叠,点B落在点处,连接,,设,.变化长方形的大小如图2所示,若的值增大了,且保持不变,则的值( )
A.增大了 B.减小了 C.增大了 D.减小了
2.下列标志中,可以看作是轴对称图形的是( )
A. B. C. D.
3.以下会徽是轴对称图形的是( ).
A. B.
C. D.
4.下列国产车标属于轴对称图形的是( )
A. B. C. D.
5.下列常见平面图形不是轴对称图形的是( )
A. B. C. D.
6.下列说法中,正确的是( )
A.等腰直角三角形不是轴对称图形 B.角的平分线是角的对称轴
C.线段的垂直平分线是线段的一条对称轴 D.轴对称图形是由两个图形组成的
7.在下列图形中,为轴对称图形的是( )
A. B. C. D.
8.下列图形中对称轴最多的是( )
A. B.
C. D.
9.下列城市的地铁图标中,不是轴对称图形的是( )
A. B. C. D.
10.如图是同学们生活中常见的品牌,其中,不是轴对称图形的是( )
A. B. C. D.
11.如图,将四边形纸片ABCD沿MN折叠,点A、D分别落在点A1、D1处.若∠1+∠2=130°,则∠B+∠C=( )
A.115° B.130° C.135 ° D.150°
12.如图,在中,点,分别是,上两点,将沿折叠,使点落在点处,若,,则的度数是( )
A. B. C. D.
二、填空题
13.如图,点P是内一点,点Q,R分别是点P关于,的对称点,与交于点M,与交于点N.若已知的周长为8cm,则 .
14.如图,将一张长方形纸片折叠成如图所示的形状,若,则的度数为
15.有一条长的卷尺.若在刻度4处折叠(如图1所示),折叠后,在重叠部分刻度为2和6的位置用剪刀剪开(如图2所示),可将该卷尺剪成三段.若小桐将该卷尺在刻度30处折叠,并在整数刻度处剪开,她剪下的三段卷尺中的两段,其中一段是另一段的3倍,则剪开处的刻度可以是 .(写出其中一种即可)
16.在图中涂黑一个小正方形,使得图中黑色的正方形成为轴对称图形,这样的小正方形可以有 个
17.如图,把一张长方形的纸片分别沿、折叠,折叠后的与在同一条直线上,则的值是 .
18.如图,已知Rt△ABC中,∠B=90°,∠A=60°,AC=2,点M、N分别在线段AC、AB上,将△AMN沿直线MN折叠,使点A的对应点D恰好落在线段BC上,当△DCM为直角三角形时,则AN的长为 .
19.如图,把一个长方形纸片沿折叠后,点C、D分别落在M、N的位置,若,则等于 .
20.若点,关于轴对称,则的值为 .
三、解答题
21.(1)将一张长方形纸片按如图1所示的方式折叠,、为折痕,求的度数;
(2)将一张长方形纸片按如图2所示的方式折叠,、为折痕,若,求的度数;
(3)将一张长方形纸片按如图3所示的方式折叠,、为折痕,若,请直接写出的度数(用含的式子表示)
22.如图,点P在四边形的内部,且点P与点M关于对称,交于点G,点P与点N关于对称,交于点H,分别交于点.
(1)连接,若求的周长;
(2)若,求的度数.
23.如图①,将一张长方形纸片沿EF对折,使AB落在的位置;
(1)若∠1的度数为a,试求∠2的度数(用含a的代数式表示);
(2)如图②,再将纸片沿GH对折,使得CD落在的位置.
①若,∠1的度数为a,试求∠3的度数(用含a的代数式表示):
②若,∠3的度数比∠1的度数大20°,试计算∠1的度数.
24.小明同学学习了轴对称后,忽然想起了做过的一道题:如图,有一组数排列成方阵,试计算这组数的和.小明想方阵就像正方形,正方形是轴对称图形,能不能用轴对称的思想来解决方阵的计算问题呢?小明试了试,竞得到非常巧妙的方法,你也能试试看吗?
参考答案:
1.C
【详解】解:∵将长方形ABCD沿CE(点E在AB上,不与点A,B重合)折叠,点B落在点处,
∴,
∵,
∴,
∵,
∴,
∵的值增大了,
∴,
∴的值增大了,
2.C
【详解】解:A、B、D选项中的汉字都不能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形;C选项中的汉字能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形;
3.A
【详解】解:A. 是轴对称图形;
B.不是轴对称图形;
C.不是轴对称图形;
D.不是轴对称图形,
4.A
【详解】A、是轴对称图形,故正确;
B、不是轴对称图形,故错误;
C、不是轴对称图形,故错误;
D、不是轴对称图形,故错误.
5.C
【详解】A.等腰三角形是轴对称图形,故A不符合题意;
B.正方形是轴对称图形,故B不符合题意;
C.平行四边形不是轴对称图形,故C符合题意;
D.圆形是轴对称图形,故D不符合题意.
6.C
【详解】解:A、等腰直角三角形是轴对称图形,原说法错误,不符合题意.
B、角的平分线所在的直线是角的对称轴,原说法错误,不符合题意.
C、线段的垂直平分线是线段的一条对称轴,正确,符合题意.
D、轴对称图形是由一个图形组成的,原说法错误,不符合题意.
7.C
【详解】如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形(axially symmetric figure),这条直线叫做对称轴(axis of symmetric);这时,我们也说这个图形 关于这条直线的轴对称.C图符合
8.A
【详解】解:圆有无数条对称轴,正六边形有条对称轴,正方形有4条对称轴,等边三角形有3条对称轴,
9.D
【详解】解:A.是轴对称图形,故本选项不合题意;
B.是轴对称图形,故本选项不合题意;
C.是轴对称图形,故本选项不合题意;
D.不是轴对称图形,故本选项符合题意;
10.B
【详解】解:A、是轴对称图形,不符合题意;
B、不是轴对称图形,符合题意;
C、是轴对称图形,不符合题意;
D、是轴对称图形,不符合题意;
11.A
【详解】解:∵∠1+∠2=130°,
∴∠AMN+∠DNM=,
∵∠A+∠D+∠AMN+∠DNM=360°,∠A+∠D+∠B+∠C=360°,
∴∠B+∠C=∠AMN+∠DNM=115°,
12.C
【详解】解:由折叠可得:,,
,
,
,
,
,
,
.
13.8cm
【详解】解:点,分别是点关于射线,的对称点,
,,
的周长,
的周长为,
.
14./40度
【详解】解:∵四边形是长方形,
∴,,
∴
由折叠的性质可得出:,,
∴,,
∴,
∴,
又∵,
∴,
15.12和48或25和35或9和51(写出其中任意一组即可)
【详解】解:设在重叠部分刻度为和的位置用剪刀剪开,则剪下的三段卷尺的长分别为,,
①取 ,,则或,
解得:(不符合题意,舍去)或,
,
剪开处的刻度可以是12和48;
②取,,则或,
解得:(不符合题意,舍去)或(不符合题意,舍去);
③取,,则或,
解得:,,
当时,;
当时,,
剪开处的刻度可以是9和51,25和35.
16.3
【详解】如图,涂黑一个小正方形,使得图中黑色的正方形成为轴对称图形,这样的小正方形共有3个.
故答案为:3.
17.90°
【详解】解:∵△B'ME是△BME沿直线EM翻折变换而成,四边形CMFD'是四边形CMFD翻折变换而成,
∴∠BME=∠B'ME=∠BMB',∠CMF=∠C'MF=∠CMC',
∵∠BMB'+∠CMC'=180°,
∴∠B'ME+∠C'MF=90°,
∴∠EMF=90°.
18.或4﹣6.
【详解】解:分两种情况:
①如图,当∠CDM=90°时,△CDM是直角三角形,
∵在Rt△ABC中,∠B=90°,∠A=60°,AC=2,
∴∠C=30°,AB=AC=,
由折叠可得,∠MDN=∠A=60°,
∴∠BDN=30°,
∴BN=DN=AN,
∴BN=AB=,
∴AN=2BN=;
②如图,当∠CMD=90°时,△CDM是直角三角形,
由题意可得,∠CDM=60°,∠A=∠MDN=60°,
∴∠BDN=60°,∠BND=30°,
∴BD=DN=AN,BN=BD,
又∵AB=,
∴2BD+BD=,
解得:BD=2﹣3,
∴AN=2BD=4﹣6;
19.52°/52度
【详解】解:∵∠EFB=64°,ADCB,
∴∠DEF=64°,
由折叠可得∠NEF=∠DEF=64°,
∴∠AEN=180°-64°-64°=52°,
20.
【详解】解: 点,关于轴对称,
21.(1);(2);(3).
【详解】解:(1)由折叠的性质知,,
∴,,
∴;
(2)由折叠的性质知,,
∴,,
∵,
∴,
∴;
(3)由折叠的性质知,,
∴,,
∵,
∴,则,
∴.
22.(1)12cm (2)134°
【详解】(1)如图,∵点P与点M关于对称,
∴,
∵点P与点N关于对称,
∴,
∵,
∴的周长为.
(2)解:∵点P与点M 关于对称,
∴,
即,
∵点P 与点N 关于 对称,
∴,
即,
∵,,
∴,
∵,
∴.
23.(1);(2)①;②50°
【详解】解:(1)如图,
由题意可知,A′E//B′F,
∴∠4=∠1=α,
∵AD//BC,
∴∠4=∠B′FC=α,
由折叠的性质可知,∠2=∠BFE,
∵∠BFE+∠2+∠B′FC=180°,
∴∠2=×(180°-α)=;
(2)①由(1)知,∠BFE=90°-α,
∵EF//C′G,
∴∠BFE=∠C′GB=,
再由折叠的性质可知,∠3+∠HGC=180°-,
∴∠3=∠HGC=;
②由(1)知,∠BFE=∠EFB′=90°-∠1,
由B′F⊥C′G可知,∠B′FC+∠FGC′=90°,
∴180°-2×(90°-∠1)+(180°-2∠3)=90°,
即∠1+180°-2∠3=90°,
∵∠3=∠1+20°,
∴∠1=50°.
24.【详解】解:从方阵中的数看出,一条对角线上的数都是5,把这条对角线当作轴,把正方形翻折一下,对称位置的两数之和都是10,
所以这样方阵中数的和=10×(1+2+3+4)+5×5=10×10+25=100+25=125.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
