人教版八年级上册数学同步练习卷 13.1.2 线段的垂直平分线的性质(含解析)
文档属性
| 名称 | 人教版八年级上册数学同步练习卷 13.1.2 线段的垂直平分线的性质(含解析) |  | |
| 格式 | docx | ||
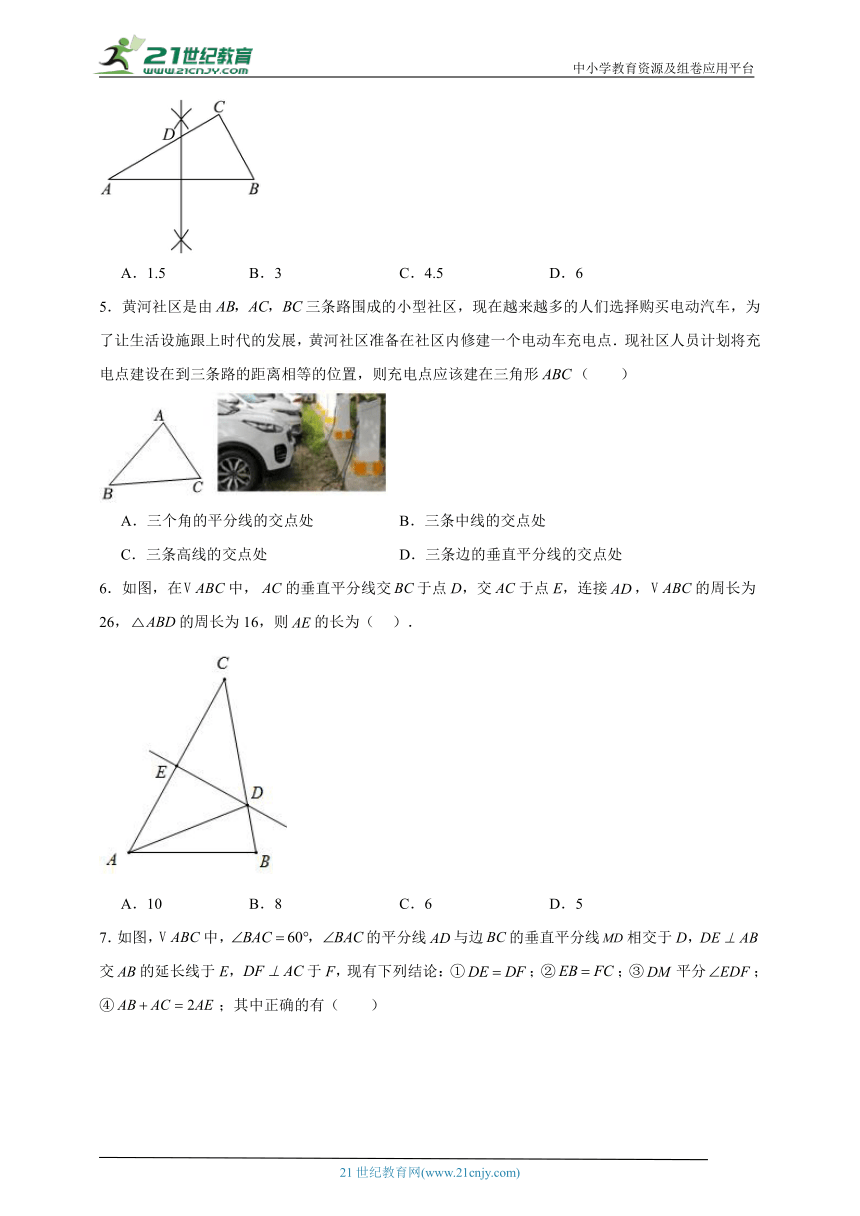
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
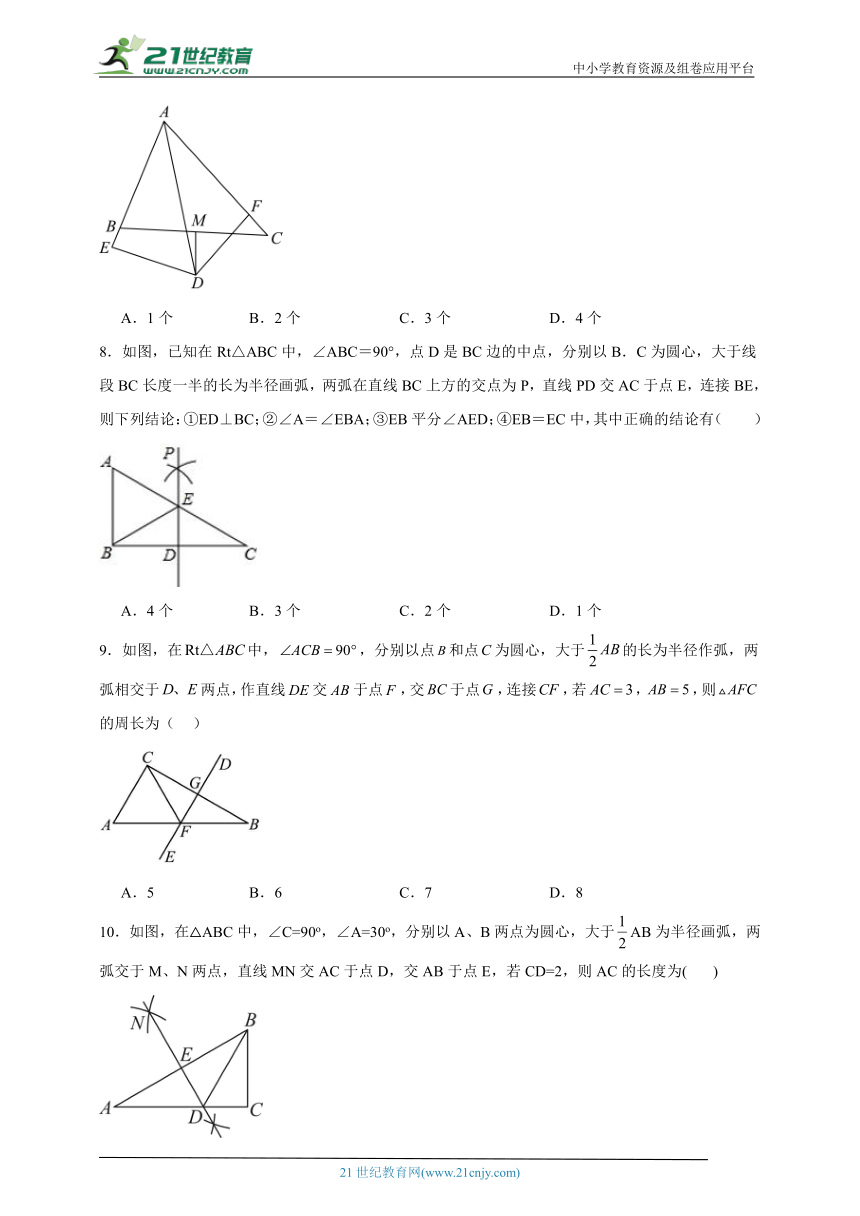
| 更新时间 | 2024-08-08 10:32:27 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
人教版八年级上册数学同步练习卷
13.1.2 线段的垂直平分线的性质
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列结论正确的个数有( )
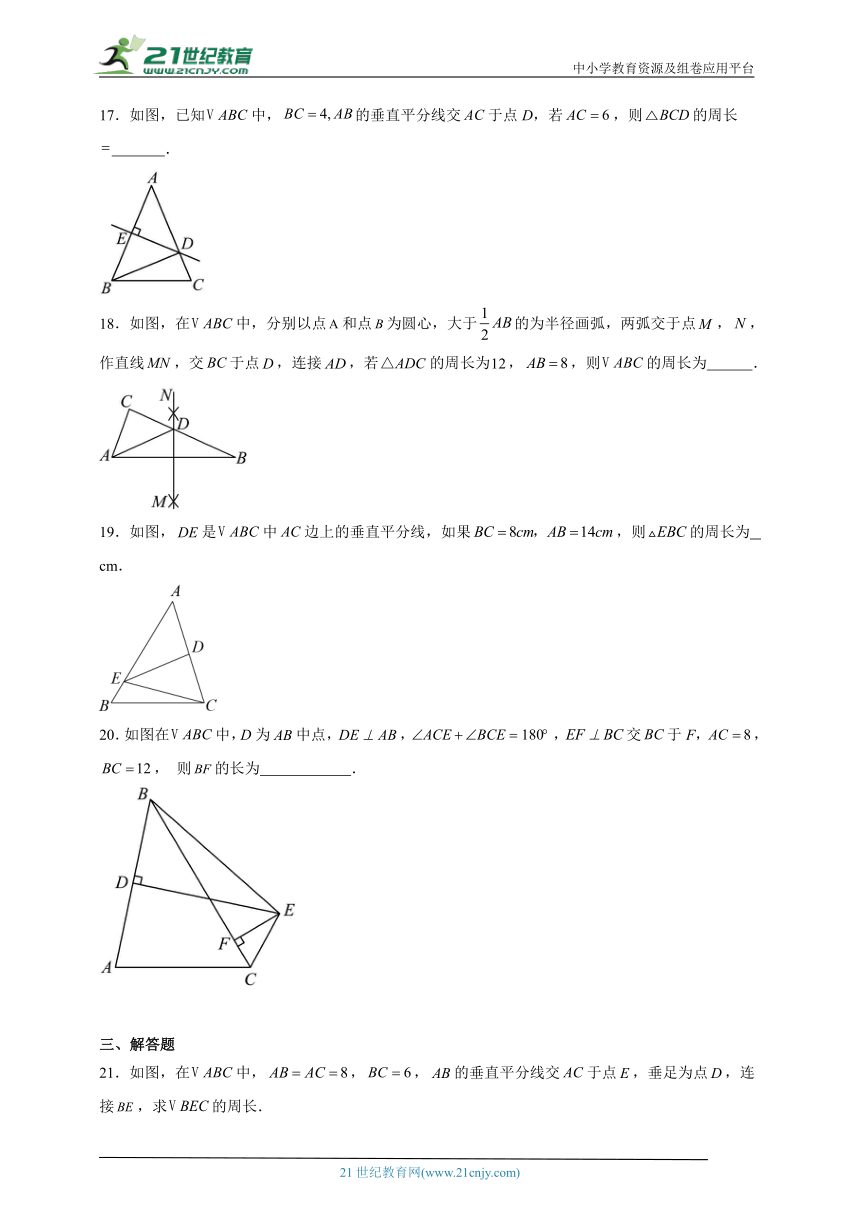
①有两边和一角对应相等的两个三角形全等;
②三角形三边的垂直平分线相交于一点;
③有两边对应相等的两个直角三角形全等;
④直线不是轴对称图形.
A.0个 B.1 个 C.2个 D.3个
2.如图所示,线段AC的垂直平分线交线段AB于点D,∠A=50°,则∠BDC=( )
A.50° B.100° C.120° D.130°
3.如图,由作图痕迹做出如下判断,其中正确的是( )
A. B. C. D.
4.如图,在中,,,用直尺和圆规作线段的垂直平分线交于点D,若,则的长为( )
A.1.5 B.3 C.4.5 D.6
5.黄河社区是由三条路围成的小型社区,现在越来越多的人们选择购买电动汽车,为了让生活设施跟上时代的发展,黄河社区准备在社区内修建一个电动车充电点.现社区人员计划将充电点建设在到三条路的距离相等的位置,则充电点应该建在三角形( )
A.三个角的平分线的交点处 B.三条中线的交点处
C.三条高线的交点处 D.三条边的垂直平分线的交点处
6.如图,在中,的垂直平分线交于点D,交于点E,连接,的周长为26,的周长为16,则的长为( ).
A.10 B.8 C.6 D.5
7.如图,中,的平分线与边的垂直平分线相交于D,交的延长线于E,于F,现有下列结论:①;②;③平分;④;其中正确的有( )
A.1个 B.2个 C.3个 D.4个
8.如图,已知在Rt△ABC中,∠ABC=90°,点D是BC边的中点,分别以B.C为圆心,大于线段BC长度一半的长为半径画弧,两弧在直线BC上方的交点为P,直线PD交AC于点E,连接BE,则下列结论:①ED⊥BC;②∠A=∠EBA;③EB平分∠AED;④EB=EC中,其中正确的结论有( )
A.4个 B.3个 C.2个 D.1个
9.如图,在中,,分别以点和点为圆心,大于的长为半径作弧,两弧相交于两点,作直线交于点,交于点,连接,若,,则的周长为( )
A.5 B.6 C.7 D.8
10.如图,在△ABC中,∠C=90o,∠A=30o,分别以A、B两点为圆心,大于AB为半径画弧,两弧交于M、N两点,直线MN交AC于点D,交AB于点E,若CD=2,则AC的长度为( )
A.9 B.6 C. D.
11.如图,若的周长为17,且边的垂直平分线分别交于,则对的周长描述正确的是( )
A.周长为17 B.周长为11 C.周长为11或17 D.周长不可求
12.如图,直线DE是ABC边AC的垂直平分线,且与AC相交于点E,与AB相交于点D,连接CD,已知BC=8cm,AB=12cm,则BCD的周长为( )
A.16cm B.18cm C.20cm D.22cm
二、填空题
13.如图,△ABC中,DE垂直平分BC,垂足为E,交AB于D,若AB=10 cm,AC=6 cm,则△ACD的周长为 cm.
14.如图,线段CD与线段BE互相垂直平分,,,则 .
15.“线段垂直平分线上的点到这条线段两个端点的距离相等”的逆命题 ,逆命题为 命题(填真、假)
16.△ABC中,AB、AC的垂直平分线分别交BC于点E、F,若∠BAC=115°,则∠EAF= .
17.如图,已知中,的垂直平分线交于点D,若,则的周长 .
18.如图,在中,分别以点和点为圆心,大于的为半径画弧,两弧交于点,,作直线,交于点,连接,若的周长为,,则的周长为 .
19.如图,是中边上的垂直平分线,如果,则的周长为 cm.
20.如图在中,D为中点,,,交于F,,, 则的长为 .
三、解答题
21.如图,在中,,,的垂直平分线交于点,垂足为点,连接,求的周长.
22.如图,在中,,分别以、为圆心,大于长为半径画弧,两弧相交于点、,作直线,与交于点,与交于点,连接.
(1)由作图可知:直线是线段的________;
(2)当,________;
(3)当,时,求的周长.
23.圣母大学计算机系的史戈宇教授带一家人去旅行,途中汽车被劫走报警911,警察无作为,汽车上安装的MS系统,可以提示汽车与手机APP间的直线距离.史教授用“贪心算法”把被盗车辆位置确定在了图中灰色的区域里,这是一个以暴乱和枪击闻名的地区.当史教授开车从E向A的方向行驶时,汽车与手机APP间的直线距离逐渐变小,从A向F的方向行驶时,汽车与手机APP问的直线距离逐渐变大.当史教授开车从F向B的方向行驶时,汽车与手机APP间的直线距离逐渐变小,从B向G的方向行驶时,汽车与手机APP间的直线距离逐渐变大. 史教授再次报警后,警察根据史教授确定的被盗汽车的位置,很快找到了被盗汽车根据你学的数学知识,在图中,画出被盗汽车的位置.
24.计算
(1).
(2).
(3)如图,已知:,,,求证:.
(4)如图,电信部门要在S区修建一座电视信号发射塔P,按照设计要求,发射塔到两个城镇A,B的距离必须相等,到两条高速公路m、n的距离也必须相等.试问发射塔应修在哪儿?在图上标出P点位置.(保留痕迹,不写作法)
参考答案:
1.C
【详解】试题分析:此题主要考查了三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
根据全等三角形的判定SAS定理可得①错误;根据线段垂直平分线的定义可得等边三角形三边的垂直平分线相交于一点,故②错误;根据直角三角形的判定定理可得③正确;根据轴对称图形的概念可得④正确.
解:①有两边和一角对应相等的两个三角形全等,说法错误,必须是夹角;
②三角形三边的垂直平分线相交于一点,说法错误;
③有两边对应相等的两个直角三角形全等,说法正确;
④直线不是轴对称图形,说法正确;
2.B
【详解】解:∵DE是线段AC的垂直平分线,
∴DA=DC,
∴∠DCA=∠A=50°,
∴∠BDC=∠DCA+∠A=100°,
3.D
【详解】解:根据作法得:PC平分∠APB,DE垂直平分PQ,
∴无法判断与的大小关系,故A、B选项不符合题意;
过点H作HM⊥AP于点M,如图,
∵PC平分∠APB,DE⊥PQ,
∴HM=HG,
在中,,
∴,故C选项不符合题意,D选项符合题意;
4.B
【详解】解:连接,如图,
∵点D为的垂直平分线与的交点,
∴,
∴,
∵,,
∴,
∴,
∴,
∴.
5.A
【详解】解:现社区人员计划将充电点建设在到三条路的距离相等的位置,则充电点应该建在三角形三个角的平分线的交点处,
6.D
【详解】解:∵的垂直平分线交于点D,交于点E,
∴AD=CD,
∴△ABD的周长=AB+AD+BD=AB+BC=16,
∵△ABC的周长=AC+BC+AB=26,
∴AC=△ABC的周长-△ACE的周长=26-16=10,
∴,
7.C
【详解】解:∵为的平分线,
∴.
∵,,
∴.
又∵,
∴,
∴,故①正确;
如图,连接,
∵为的垂直平分线,
∴,
∴,
∴,故②正确;
∵,
∴,即平分.
∵与不重合,
∴不平分,故③错误;
∵,
∴.
∵,,
∴,故④正确.
综上可知正确的有3个.
8.B
【详解】由作法得DE垂直平分BC,即ED⊥BC,所以①正确;
∴EB=EC,所以④正确;
∴∠EBC=∠C,
∵∠A+∠C=90°,∠EBA+∠EBC=90°,
∴∠A=∠EBA,所以②正确;
∵点D是BC边的中点,
∴DE为△ABC的中位线,
∴DE=AB,DE∥AB,
∴∠ABE=∠BED,
只有当∠A=60°时,∠ABE=∠AEB,BE平分∠AED,所以③不一定正确.
9.D
【详解】解:由作图可知,直线垂直平分,
∴,
∵,
∴的周长.
10.B
【详解】解:由作法得MN垂直平分AB,
∴DA=DB,
∴∠ABD=∠A=30°,
∵∠ABC=60°,
∴∠CBD=30°,
∴BD=2CD=4
∴AC=AD+CD=BD+CD=4+2=6.
11.B
【详解】解:的周长为17,
∴
垂直平分,
,
的周长
12.C
【详解】解:∵直线DE是AC的垂直平分线,
∴AD=CD,
∵BC=8cm,AB=12cm,
∴△BCD的周长=BC+CD+BD
=BC+AD+BD
=BC+AB
=8+12
=20(cm),
13.16
【详解】解:∵DE垂直平分BC
∴BD=CD
∵AB=10cm,AC=6 cm
∴△ACD的周长为AC+AD+DC=AC+AB=16cm.
14.72°
【详解】解:∵线段CD与线段BE互相垂直平分,
∴,
∴,
∵,
∴,
∴,
∴,
即:,
∵线段CD与线段BE互相垂直平分,
∴AC=AD,
∴,
∴.
15. 到线段两个端点的距离相等的点在这条线段垂直平分线上 真
【详解】解:命题“线段垂直平分线上的点到这条线段两个端点的距离相等”的逆命题是:到线段两个端点的距离相等的点在这条线段垂直平分线上,它是真命题,
16.50°
【详解】AB、AC的垂直平分线分别交BC于点E,F,
所以:(1)EA=EB,则∠B=∠EAG,
设∠B=∠EAG=x度,
(2)FA=FC,则∠C=∠FAH,
设∠C=∠FAH=y,
因为∠BAC=115°,
所以x+y+∠EAF=115°,
根据三角形内角和定理,x+y+x+y+∠EAF=180°,
解得∠EAF=50°.
17.10
【详解】解:∵是线段的垂直平分线,
∴,
∴的周长,
18.
【详解】解:∵分别以点和点为圆心,大于的为半径画弧,两弧交于点,,作直线,交于点,连接,
∴是直线的垂直平分线,
∴,
∵若的周长为12,
∴,
∴,
∵,
∴的周长为:,
19.22
【详解】解:是中边上的垂直平分线,
,
,
的周长为:(cm).
20.
【详解】解:如图,连接,过点E作交的延长线于点G,
为中点,,
,
,
,
,
,,
,
在和中,
,
(),
,
同理可得:,
,
,
,
解得:,
,
21.的周长为14.
【详解】解:是的垂直平分线,
,
周长,
,,
周长.
22.(1)垂直平分线 (2) (3)7
【详解】(1)解:由作图痕迹可知,直线是线段的垂直平分线;
(2)根据(1)得,,则,
∴,
则;
(3)
.
23.【详解】解:如图,连接EF,FG,分别过点A,B作EF,FG的垂线AN,BM,直线AN,BM交于点P,点P即为被盗汽车的位置.
24.(1) (2)
【详解】(1)
;
(2)
;
(3)∵,
∴,
∴,
∵,,
∴,
∴;
(4)设两条高速公路m、n的交于点E,以E为圆心画圆,分别交高速公路m、n于点M、N,再分别以M、N为圆心,以大于一半的长度为半径画圆弧,两弧交于点F,连接;连接,再分别以A、B为圆心,以大于一半的长度为半径画圆弧,两弧分别交于点G、H,连接,交于点P,作图如下:
即P点即为所求.
根据作图可知:是线段垂直平分线,是的角平分线,
又∵交于点P,
∴根据垂直平分线和角平分线的性质可知:点P到两个城镇A,B的距离相等,到两条高速公路m、n的距离也相等,
∴即P点即为所求.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
人教版八年级上册数学同步练习卷
13.1.2 线段的垂直平分线的性质
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列结论正确的个数有( )
①有两边和一角对应相等的两个三角形全等;
②三角形三边的垂直平分线相交于一点;
③有两边对应相等的两个直角三角形全等;
④直线不是轴对称图形.
A.0个 B.1 个 C.2个 D.3个
2.如图所示,线段AC的垂直平分线交线段AB于点D,∠A=50°,则∠BDC=( )
A.50° B.100° C.120° D.130°
3.如图,由作图痕迹做出如下判断,其中正确的是( )
A. B. C. D.
4.如图,在中,,,用直尺和圆规作线段的垂直平分线交于点D,若,则的长为( )
A.1.5 B.3 C.4.5 D.6
5.黄河社区是由三条路围成的小型社区,现在越来越多的人们选择购买电动汽车,为了让生活设施跟上时代的发展,黄河社区准备在社区内修建一个电动车充电点.现社区人员计划将充电点建设在到三条路的距离相等的位置,则充电点应该建在三角形( )
A.三个角的平分线的交点处 B.三条中线的交点处
C.三条高线的交点处 D.三条边的垂直平分线的交点处
6.如图,在中,的垂直平分线交于点D,交于点E,连接,的周长为26,的周长为16,则的长为( ).
A.10 B.8 C.6 D.5
7.如图,中,的平分线与边的垂直平分线相交于D,交的延长线于E,于F,现有下列结论:①;②;③平分;④;其中正确的有( )
A.1个 B.2个 C.3个 D.4个
8.如图,已知在Rt△ABC中,∠ABC=90°,点D是BC边的中点,分别以B.C为圆心,大于线段BC长度一半的长为半径画弧,两弧在直线BC上方的交点为P,直线PD交AC于点E,连接BE,则下列结论:①ED⊥BC;②∠A=∠EBA;③EB平分∠AED;④EB=EC中,其中正确的结论有( )
A.4个 B.3个 C.2个 D.1个
9.如图,在中,,分别以点和点为圆心,大于的长为半径作弧,两弧相交于两点,作直线交于点,交于点,连接,若,,则的周长为( )
A.5 B.6 C.7 D.8
10.如图,在△ABC中,∠C=90o,∠A=30o,分别以A、B两点为圆心,大于AB为半径画弧,两弧交于M、N两点,直线MN交AC于点D,交AB于点E,若CD=2,则AC的长度为( )
A.9 B.6 C. D.
11.如图,若的周长为17,且边的垂直平分线分别交于,则对的周长描述正确的是( )
A.周长为17 B.周长为11 C.周长为11或17 D.周长不可求
12.如图,直线DE是ABC边AC的垂直平分线,且与AC相交于点E,与AB相交于点D,连接CD,已知BC=8cm,AB=12cm,则BCD的周长为( )
A.16cm B.18cm C.20cm D.22cm
二、填空题
13.如图,△ABC中,DE垂直平分BC,垂足为E,交AB于D,若AB=10 cm,AC=6 cm,则△ACD的周长为 cm.
14.如图,线段CD与线段BE互相垂直平分,,,则 .
15.“线段垂直平分线上的点到这条线段两个端点的距离相等”的逆命题 ,逆命题为 命题(填真、假)
16.△ABC中,AB、AC的垂直平分线分别交BC于点E、F,若∠BAC=115°,则∠EAF= .
17.如图,已知中,的垂直平分线交于点D,若,则的周长 .
18.如图,在中,分别以点和点为圆心,大于的为半径画弧,两弧交于点,,作直线,交于点,连接,若的周长为,,则的周长为 .
19.如图,是中边上的垂直平分线,如果,则的周长为 cm.
20.如图在中,D为中点,,,交于F,,, 则的长为 .
三、解答题
21.如图,在中,,,的垂直平分线交于点,垂足为点,连接,求的周长.
22.如图,在中,,分别以、为圆心,大于长为半径画弧,两弧相交于点、,作直线,与交于点,与交于点,连接.
(1)由作图可知:直线是线段的________;
(2)当,________;
(3)当,时,求的周长.
23.圣母大学计算机系的史戈宇教授带一家人去旅行,途中汽车被劫走报警911,警察无作为,汽车上安装的MS系统,可以提示汽车与手机APP间的直线距离.史教授用“贪心算法”把被盗车辆位置确定在了图中灰色的区域里,这是一个以暴乱和枪击闻名的地区.当史教授开车从E向A的方向行驶时,汽车与手机APP间的直线距离逐渐变小,从A向F的方向行驶时,汽车与手机APP问的直线距离逐渐变大.当史教授开车从F向B的方向行驶时,汽车与手机APP间的直线距离逐渐变小,从B向G的方向行驶时,汽车与手机APP间的直线距离逐渐变大. 史教授再次报警后,警察根据史教授确定的被盗汽车的位置,很快找到了被盗汽车根据你学的数学知识,在图中,画出被盗汽车的位置.
24.计算
(1).
(2).
(3)如图,已知:,,,求证:.
(4)如图,电信部门要在S区修建一座电视信号发射塔P,按照设计要求,发射塔到两个城镇A,B的距离必须相等,到两条高速公路m、n的距离也必须相等.试问发射塔应修在哪儿?在图上标出P点位置.(保留痕迹,不写作法)
参考答案:
1.C
【详解】试题分析:此题主要考查了三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
根据全等三角形的判定SAS定理可得①错误;根据线段垂直平分线的定义可得等边三角形三边的垂直平分线相交于一点,故②错误;根据直角三角形的判定定理可得③正确;根据轴对称图形的概念可得④正确.
解:①有两边和一角对应相等的两个三角形全等,说法错误,必须是夹角;
②三角形三边的垂直平分线相交于一点,说法错误;
③有两边对应相等的两个直角三角形全等,说法正确;
④直线不是轴对称图形,说法正确;
2.B
【详解】解:∵DE是线段AC的垂直平分线,
∴DA=DC,
∴∠DCA=∠A=50°,
∴∠BDC=∠DCA+∠A=100°,
3.D
【详解】解:根据作法得:PC平分∠APB,DE垂直平分PQ,
∴无法判断与的大小关系,故A、B选项不符合题意;
过点H作HM⊥AP于点M,如图,
∵PC平分∠APB,DE⊥PQ,
∴HM=HG,
在中,,
∴,故C选项不符合题意,D选项符合题意;
4.B
【详解】解:连接,如图,
∵点D为的垂直平分线与的交点,
∴,
∴,
∵,,
∴,
∴,
∴,
∴.
5.A
【详解】解:现社区人员计划将充电点建设在到三条路的距离相等的位置,则充电点应该建在三角形三个角的平分线的交点处,
6.D
【详解】解:∵的垂直平分线交于点D,交于点E,
∴AD=CD,
∴△ABD的周长=AB+AD+BD=AB+BC=16,
∵△ABC的周长=AC+BC+AB=26,
∴AC=△ABC的周长-△ACE的周长=26-16=10,
∴,
7.C
【详解】解:∵为的平分线,
∴.
∵,,
∴.
又∵,
∴,
∴,故①正确;
如图,连接,
∵为的垂直平分线,
∴,
∴,
∴,故②正确;
∵,
∴,即平分.
∵与不重合,
∴不平分,故③错误;
∵,
∴.
∵,,
∴,故④正确.
综上可知正确的有3个.
8.B
【详解】由作法得DE垂直平分BC,即ED⊥BC,所以①正确;
∴EB=EC,所以④正确;
∴∠EBC=∠C,
∵∠A+∠C=90°,∠EBA+∠EBC=90°,
∴∠A=∠EBA,所以②正确;
∵点D是BC边的中点,
∴DE为△ABC的中位线,
∴DE=AB,DE∥AB,
∴∠ABE=∠BED,
只有当∠A=60°时,∠ABE=∠AEB,BE平分∠AED,所以③不一定正确.
9.D
【详解】解:由作图可知,直线垂直平分,
∴,
∵,
∴的周长.
10.B
【详解】解:由作法得MN垂直平分AB,
∴DA=DB,
∴∠ABD=∠A=30°,
∵∠ABC=60°,
∴∠CBD=30°,
∴BD=2CD=4
∴AC=AD+CD=BD+CD=4+2=6.
11.B
【详解】解:的周长为17,
∴
垂直平分,
,
的周长
12.C
【详解】解:∵直线DE是AC的垂直平分线,
∴AD=CD,
∵BC=8cm,AB=12cm,
∴△BCD的周长=BC+CD+BD
=BC+AD+BD
=BC+AB
=8+12
=20(cm),
13.16
【详解】解:∵DE垂直平分BC
∴BD=CD
∵AB=10cm,AC=6 cm
∴△ACD的周长为AC+AD+DC=AC+AB=16cm.
14.72°
【详解】解:∵线段CD与线段BE互相垂直平分,
∴,
∴,
∵,
∴,
∴,
∴,
即:,
∵线段CD与线段BE互相垂直平分,
∴AC=AD,
∴,
∴.
15. 到线段两个端点的距离相等的点在这条线段垂直平分线上 真
【详解】解:命题“线段垂直平分线上的点到这条线段两个端点的距离相等”的逆命题是:到线段两个端点的距离相等的点在这条线段垂直平分线上,它是真命题,
16.50°
【详解】AB、AC的垂直平分线分别交BC于点E,F,
所以:(1)EA=EB,则∠B=∠EAG,
设∠B=∠EAG=x度,
(2)FA=FC,则∠C=∠FAH,
设∠C=∠FAH=y,
因为∠BAC=115°,
所以x+y+∠EAF=115°,
根据三角形内角和定理,x+y+x+y+∠EAF=180°,
解得∠EAF=50°.
17.10
【详解】解:∵是线段的垂直平分线,
∴,
∴的周长,
18.
【详解】解:∵分别以点和点为圆心,大于的为半径画弧,两弧交于点,,作直线,交于点,连接,
∴是直线的垂直平分线,
∴,
∵若的周长为12,
∴,
∴,
∵,
∴的周长为:,
19.22
【详解】解:是中边上的垂直平分线,
,
,
的周长为:(cm).
20.
【详解】解:如图,连接,过点E作交的延长线于点G,
为中点,,
,
,
,
,
,,
,
在和中,
,
(),
,
同理可得:,
,
,
,
解得:,
,
21.的周长为14.
【详解】解:是的垂直平分线,
,
周长,
,,
周长.
22.(1)垂直平分线 (2) (3)7
【详解】(1)解:由作图痕迹可知,直线是线段的垂直平分线;
(2)根据(1)得,,则,
∴,
则;
(3)
.
23.【详解】解:如图,连接EF,FG,分别过点A,B作EF,FG的垂线AN,BM,直线AN,BM交于点P,点P即为被盗汽车的位置.
24.(1) (2)
【详解】(1)
;
(2)
;
(3)∵,
∴,
∴,
∵,,
∴,
∴;
(4)设两条高速公路m、n的交于点E,以E为圆心画圆,分别交高速公路m、n于点M、N,再分别以M、N为圆心,以大于一半的长度为半径画圆弧,两弧交于点F,连接;连接,再分别以A、B为圆心,以大于一半的长度为半径画圆弧,两弧分别交于点G、H,连接,交于点P,作图如下:
即P点即为所求.
根据作图可知:是线段垂直平分线,是的角平分线,
又∵交于点P,
∴根据垂直平分线和角平分线的性质可知:点P到两个城镇A,B的距离相等,到两条高速公路m、n的距离也相等,
∴即P点即为所求.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
