人教版八年级上册数学同步练习卷 13.2 画轴对称图形(含解析)
文档属性
| 名称 | 人教版八年级上册数学同步练习卷 13.2 画轴对称图形(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 658.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-08 10:35:08 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
人教版八年级上册数学同步练习卷
13.2 画轴对称图形
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,在平面直角坐标系中,关于直线(直线上各点的坐标都为1)对称,点的坐标为,则点的坐标为( )
A. B. C. D.
2.在平面直角坐标系中,点A(﹣2,3)关于y轴对称的点A′的坐标是( )
A.(-2,6) B.(2,3) C.(-2,-3) D.(2,-3)
3.若点,,,,,是平面直角坐标系内的6个点,选择其中三个点连成一个三角形,剩下三个点连成另一个三角形,若这两个三角形关于y轴对称,称为一组对称三角形,则平面直角坐标系中可找出的对称三角形有( )
A.2组 B.3组 C.4组 D.5组
4.在坐标系中,点关于x轴对称的点的坐标为( )
A. B. C. D.
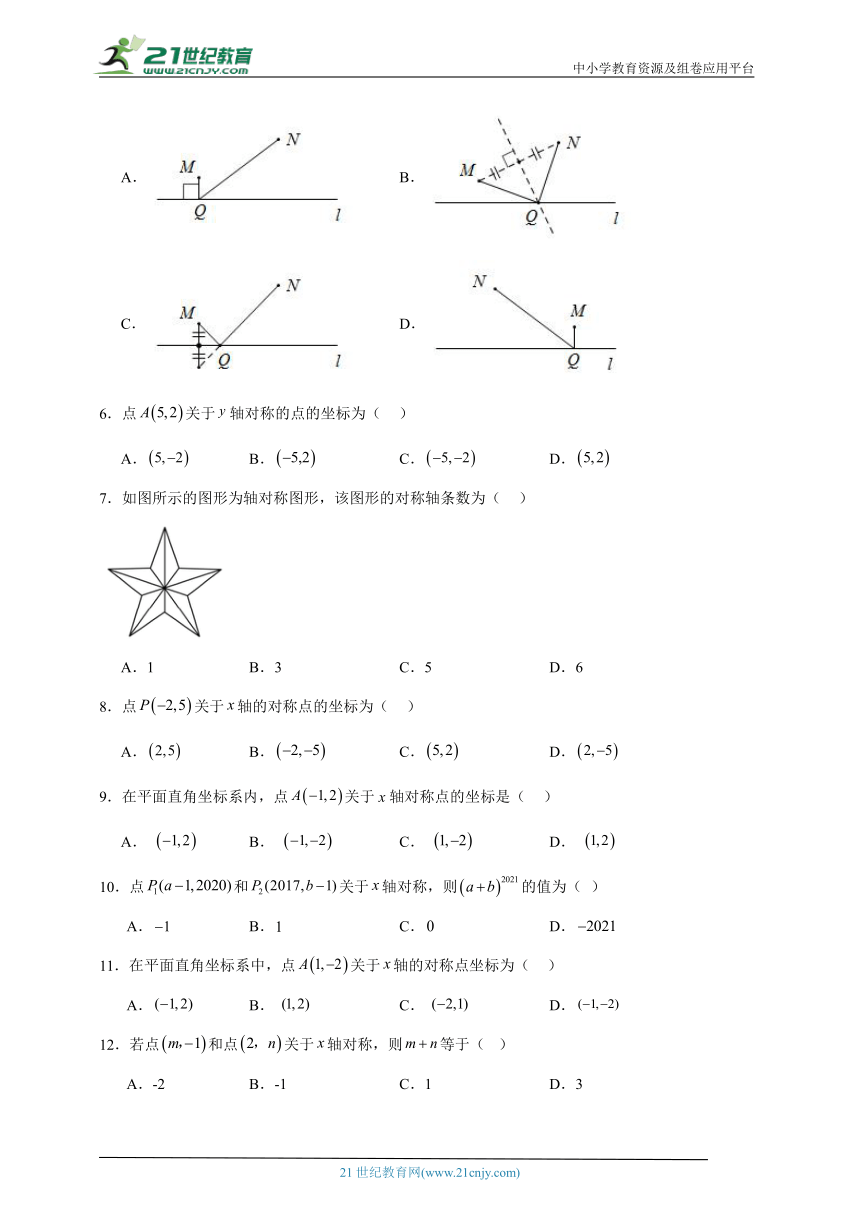
5.如图,点M,N在直线l的同侧,小东同学想通过作图在直线l上确定一点Q,使MQ与QN的和最小,那么下面的操作正确的是( )
A. B.
C. D.
6.点关于轴对称的点的坐标为( )
A. B. C. D.
7.如图所示的图形为轴对称图形,该图形的对称轴条数为( )
A.1 B.3 C.5 D.6
8.点关于轴的对称点的坐标为( )
A. B. C. D.
9.在平面直角坐标系内,点关于x轴对称点的坐标是( )
A. B. C. D.
10.点和关于轴对称,则的值为( )
A. B. C. D.
11.在平面直角坐标系中,点关于轴的对称点坐标为( )
A. B. C. D.
12.若点和点关于轴对称,则等于( )
A.-2 B.-1 C.1 D.3
二、填空题
13.在平面直角坐标系中,点A与点关于x轴对称,点A与点关于y轴对称,已知点的坐标为,则点的坐标为 .
14.若点P(a+2,3)与点Q(﹣1,b+1)关于y轴对称,则ab= .
15.在平面直角坐标系中,已知,关于y轴对称,则 .
16.在如图所示的正方形网格中,每个小正方形的边长为1各单位,格点三角形(顶点是网格线的交点的三角形)△ABC的顶点A,B的坐标分别为(1,4),(﹣3,1).
(1)请在网格所在的平面内作出符合上述表述的平面直角坐标系;
(2)请你将A、B、C的横坐标不变,纵坐标乘以﹣1所得到的点A1、B1、C1描在坐标系中,并画出△A1B1C1,其中点C1的坐标为 .
(3)△ABC的面积是 .
17.如图,有一个英语单词,四个字母都关于直线l对称,请写出这个单词 .
18.已知点A关于x轴的对称点B的坐标为(1,﹣2),则点A的坐标为 .
19.当m= 时,点P(-4,3m-5)与Q(-4,2m-10)关于x轴对称;
20.若点和点关于轴对称,则 .
三、解答题
21.已知点.
(1)若M、N关于x轴对称,试求a,b的值;
(2)若M、N关于y轴对称,试求的值.
22.如图是的正方形网格,按下列要求操作并计算.
(1)在的正方形网格中建立平面直角坐标系,使点A的坐标为,点B的坐标为.
(2)先作点A关于y轴的对称点,然后点再向下平移5个单位得到点C,画出三角形,并写出点C的坐标.
(3)填空:的面积为________.
23.已知点与关于x轴对称,求的值.
24.在一平直河岸l同侧有A,B两个村庄,A,B到l的距离分别是3km和2km,AB=akm(a>1).现计划在河岸l上建一抽水站P,用输水管向两个村庄供水.
方案设计
某班数学兴趣小组设计了两种铺设管道方案:图1是方案一的示意图,设该方案中管道长度为d1,且d1=PB+BA(km)(其中BP⊥l于点P);图2是方案二的示意图,设该方案中管道长度为d2,且d2=PA+PB(km)(其中点A′与点A关于l对称,A′B与l交于点P).
观察计算
(1)在方案一中,d1= km(用含a的式子表示)
(2)在方案二中,组长小宇为了计算d2的长,作了如图3所示的辅助线,请你按小宇同学的思路计算,d2= km(用含a的式子表示).
探索归纳
(1)①当a=4时,比较大小:d1 d2(填“>”、“=”或“<”);②当a=6时,比较大小:d1 d2(填“>”、“=”或“<”);
(2)请你参考方框中的方法指导,就a(当a>1时)的所有取值情况进行分析,要使铺设的管道长度较短,应选择方案一还是方案二?
参考答案:
1.B
【详解】解:∵△ABC关于直线m(直线m上各点的横坐标都为1)对称,
∴C,B关于直线m对称,即关于直线x=1对称,
∵点C的坐标为(4,1),
∴设B(x,1)则,解得x=-2
2.B
【详解】试题分析:关于y轴对称的两个点横坐标互为相反数,纵坐标相等.
3.C
【详解】解:分析易得,A和B的坐标,横坐标互为相反数,纵坐标相等,则A,B关于y轴对称,
同理C和D,E和F都关于y轴对称,
故在A和B,C和D,E和F三组点中,各任取一个点,连接后形成的三角形与剩下三个点连成另一个三角形是对称三角形,
进而可得,共4组不同的取法,
4.B
【详解】解:∵关于x轴对称,则横坐标不变,纵坐标变为相反数,
∴点关于x轴对称的点坐标为:,
5.C
【详解】作点M关于直线l的对称点M′,再连接M′N交l于点Q,则MQ+NQ=M′Q+NQ=M′N,由“两点之间,线段最短”,可知点Q即为所求.
6.B
【详解】解:点关于轴对称的点的坐标为.
7.C
【详解】解:由题意可知该图的对称轴如图所示:
由图可知该图形的对称轴有5条.
8.B
【详解】根据两点关于x轴对称,横坐标不变,纵坐标互为相反数,
则点P(-2,5)关于x轴的对称点P′的坐标是(-2,-5).
9.B
【详解】解:点关于轴的对称点的坐标是,
10.A
【详解】解:∵和关于轴对称,得
a-1=2017,1-b=2020.
解得a=2018,b=-2019,
∴
11.B
【详解】根据关于轴对称的点的特点:横坐标相同,纵坐标互为相反数,可知
点关于轴的对称点坐标为.
12.D
【详解】∵点和点关于轴对称,
∴m=2,n=1,
∴m+n=3,
13.
【详解】解:∵点A与点关于x轴对称,已知点,
∴点A的坐标为,
∵点A与点关于y轴对称,
∴点的坐标为,
14.﹣6.
【详解】点P(a+2,3)与点Q(-1,b+1)关于y轴对称,
a+2=-1, ,b+1=3
解得a=-3,b=2,
所以ab=(-3)2=-6
15.19
【详解】解:∵,关于y轴对称,
∴,,
∴,
16.(1)【详解】解:(1)平面直角坐标系如图所示;
(2)如图所示,△A1B1C1即为所求,其中点C1的坐标为(5,2);
(3)△ABC的面积是×6×(3+3)=18.
17.BOOK
【详解】解:如图,
这个单词是BOOK.
18.
【详解】解:∵点A关于x轴的对称点B的坐标为(1,﹣2),
∴点A的坐标为
19.3
【详解】解:由点P(-4,3m-5)与Q(-4,2m-10)关于x轴对称,得
3m-5+2m-10=0.
解得m=3
20.12
【详解】∵点和点关于轴对称,
∴,
∴,
21.(1); (2)1.
【详解】(1)解:∵M、N关于x轴对称,
∴,
解得;
(2)∵M、N关于y轴对称,
∴,
解得,
∴
22.【详解】(1)解:如图,即为所求;
(2)如图,即为所求;
其中;
(3)的面积.
23.
【详解】解:∵点与关于x轴对称,
∴,
∴,
∴.
24.观察计算:(1)a+2;(2);探索归纳:(1)①<,②>;(2)当a>5时,选方案二;当a=5时,选方案一或方案二;当1<a<5时,选方案一.
【详解】(1)由题意可得PB=2,,
d1=PB+BA=a+2;
故答案为a+2;
(2)因为BK2=a2﹣1,
A'B2=BK2+A'K2=a2﹣1+52=a2+24
∴d2=;
故答案为;
探索归纳:
(1)①当a=4时,d1=6,d2= ,d1<d2;
②当a=6时,d1=8,d2=,d1>d2;
故答案为<,>;
(2)d12﹣d22=(a+2)2﹣()2=4a﹣20.
①当4a﹣20>0,即a>5时,d12﹣d22>0,
∴d1﹣d2>0,
∴d1>d2;
②当4a﹣20=0,即a=5时,d12﹣d22=0,
∴d1﹣d2=0,
∴d1=d2
③当4a﹣20<0,即a<5时,d12﹣d22<0,
∴d1﹣d2<0,
∴d1<d2
综上可知:当a>5时,选方案二;
当a=5时,选方案一或方案二;
当1<a<5时,选方案一.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
人教版八年级上册数学同步练习卷
13.2 画轴对称图形
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,在平面直角坐标系中,关于直线(直线上各点的坐标都为1)对称,点的坐标为,则点的坐标为( )
A. B. C. D.
2.在平面直角坐标系中,点A(﹣2,3)关于y轴对称的点A′的坐标是( )
A.(-2,6) B.(2,3) C.(-2,-3) D.(2,-3)
3.若点,,,,,是平面直角坐标系内的6个点,选择其中三个点连成一个三角形,剩下三个点连成另一个三角形,若这两个三角形关于y轴对称,称为一组对称三角形,则平面直角坐标系中可找出的对称三角形有( )
A.2组 B.3组 C.4组 D.5组
4.在坐标系中,点关于x轴对称的点的坐标为( )
A. B. C. D.
5.如图,点M,N在直线l的同侧,小东同学想通过作图在直线l上确定一点Q,使MQ与QN的和最小,那么下面的操作正确的是( )
A. B.
C. D.
6.点关于轴对称的点的坐标为( )
A. B. C. D.
7.如图所示的图形为轴对称图形,该图形的对称轴条数为( )
A.1 B.3 C.5 D.6
8.点关于轴的对称点的坐标为( )
A. B. C. D.
9.在平面直角坐标系内,点关于x轴对称点的坐标是( )
A. B. C. D.
10.点和关于轴对称,则的值为( )
A. B. C. D.
11.在平面直角坐标系中,点关于轴的对称点坐标为( )
A. B. C. D.
12.若点和点关于轴对称,则等于( )
A.-2 B.-1 C.1 D.3
二、填空题
13.在平面直角坐标系中,点A与点关于x轴对称,点A与点关于y轴对称,已知点的坐标为,则点的坐标为 .
14.若点P(a+2,3)与点Q(﹣1,b+1)关于y轴对称,则ab= .
15.在平面直角坐标系中,已知,关于y轴对称,则 .
16.在如图所示的正方形网格中,每个小正方形的边长为1各单位,格点三角形(顶点是网格线的交点的三角形)△ABC的顶点A,B的坐标分别为(1,4),(﹣3,1).
(1)请在网格所在的平面内作出符合上述表述的平面直角坐标系;
(2)请你将A、B、C的横坐标不变,纵坐标乘以﹣1所得到的点A1、B1、C1描在坐标系中,并画出△A1B1C1,其中点C1的坐标为 .
(3)△ABC的面积是 .
17.如图,有一个英语单词,四个字母都关于直线l对称,请写出这个单词 .
18.已知点A关于x轴的对称点B的坐标为(1,﹣2),则点A的坐标为 .
19.当m= 时,点P(-4,3m-5)与Q(-4,2m-10)关于x轴对称;
20.若点和点关于轴对称,则 .
三、解答题
21.已知点.
(1)若M、N关于x轴对称,试求a,b的值;
(2)若M、N关于y轴对称,试求的值.
22.如图是的正方形网格,按下列要求操作并计算.
(1)在的正方形网格中建立平面直角坐标系,使点A的坐标为,点B的坐标为.
(2)先作点A关于y轴的对称点,然后点再向下平移5个单位得到点C,画出三角形,并写出点C的坐标.
(3)填空:的面积为________.
23.已知点与关于x轴对称,求的值.
24.在一平直河岸l同侧有A,B两个村庄,A,B到l的距离分别是3km和2km,AB=akm(a>1).现计划在河岸l上建一抽水站P,用输水管向两个村庄供水.
方案设计
某班数学兴趣小组设计了两种铺设管道方案:图1是方案一的示意图,设该方案中管道长度为d1,且d1=PB+BA(km)(其中BP⊥l于点P);图2是方案二的示意图,设该方案中管道长度为d2,且d2=PA+PB(km)(其中点A′与点A关于l对称,A′B与l交于点P).
观察计算
(1)在方案一中,d1= km(用含a的式子表示)
(2)在方案二中,组长小宇为了计算d2的长,作了如图3所示的辅助线,请你按小宇同学的思路计算,d2= km(用含a的式子表示).
探索归纳
(1)①当a=4时,比较大小:d1 d2(填“>”、“=”或“<”);②当a=6时,比较大小:d1 d2(填“>”、“=”或“<”);
(2)请你参考方框中的方法指导,就a(当a>1时)的所有取值情况进行分析,要使铺设的管道长度较短,应选择方案一还是方案二?
参考答案:
1.B
【详解】解:∵△ABC关于直线m(直线m上各点的横坐标都为1)对称,
∴C,B关于直线m对称,即关于直线x=1对称,
∵点C的坐标为(4,1),
∴设B(x,1)则,解得x=-2
2.B
【详解】试题分析:关于y轴对称的两个点横坐标互为相反数,纵坐标相等.
3.C
【详解】解:分析易得,A和B的坐标,横坐标互为相反数,纵坐标相等,则A,B关于y轴对称,
同理C和D,E和F都关于y轴对称,
故在A和B,C和D,E和F三组点中,各任取一个点,连接后形成的三角形与剩下三个点连成另一个三角形是对称三角形,
进而可得,共4组不同的取法,
4.B
【详解】解:∵关于x轴对称,则横坐标不变,纵坐标变为相反数,
∴点关于x轴对称的点坐标为:,
5.C
【详解】作点M关于直线l的对称点M′,再连接M′N交l于点Q,则MQ+NQ=M′Q+NQ=M′N,由“两点之间,线段最短”,可知点Q即为所求.
6.B
【详解】解:点关于轴对称的点的坐标为.
7.C
【详解】解:由题意可知该图的对称轴如图所示:
由图可知该图形的对称轴有5条.
8.B
【详解】根据两点关于x轴对称,横坐标不变,纵坐标互为相反数,
则点P(-2,5)关于x轴的对称点P′的坐标是(-2,-5).
9.B
【详解】解:点关于轴的对称点的坐标是,
10.A
【详解】解:∵和关于轴对称,得
a-1=2017,1-b=2020.
解得a=2018,b=-2019,
∴
11.B
【详解】根据关于轴对称的点的特点:横坐标相同,纵坐标互为相反数,可知
点关于轴的对称点坐标为.
12.D
【详解】∵点和点关于轴对称,
∴m=2,n=1,
∴m+n=3,
13.
【详解】解:∵点A与点关于x轴对称,已知点,
∴点A的坐标为,
∵点A与点关于y轴对称,
∴点的坐标为,
14.﹣6.
【详解】点P(a+2,3)与点Q(-1,b+1)关于y轴对称,
a+2=-1, ,b+1=3
解得a=-3,b=2,
所以ab=(-3)2=-6
15.19
【详解】解:∵,关于y轴对称,
∴,,
∴,
16.(1)【详解】解:(1)平面直角坐标系如图所示;
(2)如图所示,△A1B1C1即为所求,其中点C1的坐标为(5,2);
(3)△ABC的面积是×6×(3+3)=18.
17.BOOK
【详解】解:如图,
这个单词是BOOK.
18.
【详解】解:∵点A关于x轴的对称点B的坐标为(1,﹣2),
∴点A的坐标为
19.3
【详解】解:由点P(-4,3m-5)与Q(-4,2m-10)关于x轴对称,得
3m-5+2m-10=0.
解得m=3
20.12
【详解】∵点和点关于轴对称,
∴,
∴,
21.(1); (2)1.
【详解】(1)解:∵M、N关于x轴对称,
∴,
解得;
(2)∵M、N关于y轴对称,
∴,
解得,
∴
22.【详解】(1)解:如图,即为所求;
(2)如图,即为所求;
其中;
(3)的面积.
23.
【详解】解:∵点与关于x轴对称,
∴,
∴,
∴.
24.观察计算:(1)a+2;(2);探索归纳:(1)①<,②>;(2)当a>5时,选方案二;当a=5时,选方案一或方案二;当1<a<5时,选方案一.
【详解】(1)由题意可得PB=2,,
d1=PB+BA=a+2;
故答案为a+2;
(2)因为BK2=a2﹣1,
A'B2=BK2+A'K2=a2﹣1+52=a2+24
∴d2=;
故答案为;
探索归纳:
(1)①当a=4时,d1=6,d2= ,d1<d2;
②当a=6时,d1=8,d2=,d1>d2;
故答案为<,>;
(2)d12﹣d22=(a+2)2﹣()2=4a﹣20.
①当4a﹣20>0,即a>5时,d12﹣d22>0,
∴d1﹣d2>0,
∴d1>d2;
②当4a﹣20=0,即a=5时,d12﹣d22=0,
∴d1﹣d2=0,
∴d1=d2
③当4a﹣20<0,即a<5时,d12﹣d22<0,
∴d1﹣d2<0,
∴d1<d2
综上可知:当a>5时,选方案二;
当a=5时,选方案一或方案二;
当1<a<5时,选方案一.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
