九年级数学上册 22.3 相似三角形的性质 导学案(知识清单 典型例题 巩固提升)
文档属性
| 名称 | 九年级数学上册 22.3 相似三角形的性质 导学案(知识清单 典型例题 巩固提升) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-08 13:20:33 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
22.3 相似三角形的性质 导学案
(一)学习目标:
1.明确相似三角形中对应线段与相似比的关系.
2.掌握相似三角形的周长比等于相似比、面积比等于相似比的平方及其在实际中的应用.
(二)学习重难点
重点:明确相似三角形中对应线段与相似比的关系.
难点:相似三角形的性质定理解决简单的实际问题.
阅读课本,识记知识:
性质1:相似三角形的对应角相等,对应边对应成比例.
性质2:相似三角形中的重要线段的比等于相似比.
相似三角形对应高,对应中线,对应角平分线的比都等于相似比.
注意:要特别注意“对应”两个字,在应用时,要注意找准对应线段.
性质3:相似三角形周长的比等于相似比
如图一: ∽,则
由比例性质可得:
性质4:相似三角形面积的比等于相似比的平方
如图二,∽,则分别作出与的高和,则
注意:相似三角形的性质是通过比例线段的性质推证出来的.
射影定理
射影定理:如图,Rt△ABC,∠C=90 ,CD⊥AB
则,1.CD2=AD·BD
2.BC2=BD·AB
AC2=AD·AB
很容易推出:.
AC·BC=AB·CD.
BC2+AC2=AB2.
.
AC+BC<AB+CD.
用图中小写字母a、b、c、p、q、h(常称为勾股六线段)表达以上关系:
① h2=pq ;② a2=pc ;③ b2=qc ;④ ;⑤ ab=ch ;
⑥ a2+b2=c2 ;⑦ ;⑧ a+b<c+h;⑨ c=p+q.
利用上述关系式, “知二可求四” ,即在a、b、c、p、q、h这六个量中,已知两个量就可求出其余四个量来。同学们自己可任意设出两个量,练习求另外四个量(在设的时候,要注意构成直角三角形的基本条件:斜边大于直角边
【例1】如图,在中,中线相交于点G,下列说法错误的是( )
A.点G为的重心 B.
C.当为等边三角形时, D.
【答案】D
【分析】根据三角形的重心性质可判断选项A、B;根据等边三角形的性质得到,可判断选项C;根据三角形的中线将三角形的面积平分可判断选项D.
【详解】解:A、∵的中线相交于点G,
∴点G为的重心,故选项A正确,不符合题意;
B、∵点G 为的重心,
∴,即,故选项B正确,不符合题意;
C、∵为等边三角形,
∴,
∵,,
∴,,
∴,故选项C正确,不符合题意;
D、∵,
∴,则,
∴,故选项D错误,符合题意,
故选:D.
【点睛】本题考查三角形的重心性质、等边三角形的性质、三角形的中线性质,解答的关键是熟练掌握三角形的中线性质和重心性质:三角形的重心到顶点的距离与重心到对边中点的距离之比为.
【例2】 《笛卡尔几何学》一书中引入单位线段1来表示线段的乘除.如图,已知,则,若规定为单位线段1,则,若规定为单位线段1,则为( )
A. B. C. D.
【答案】C
【分析】由,可得,根据比例的性质可得,即,由于规定为单位线段1,则,即可解答.
【详解】解:∵,
∴,
∴,
即,
∴,
∵规定为单位线段1,
∴.
故选:C.
【点睛】本题考查相似三角形的性质,比例的性质,读懂题意,正确使用比例的性质是解题的关键.
选择题
1.若两个相似三角形的面积之比为1∶9,则它们对应角的平分线之比为 ( )
A. B.3 C. D.3
2.如图,在中,为上一点,连接,,且与相交于点,,则( )
A. B. C. D.
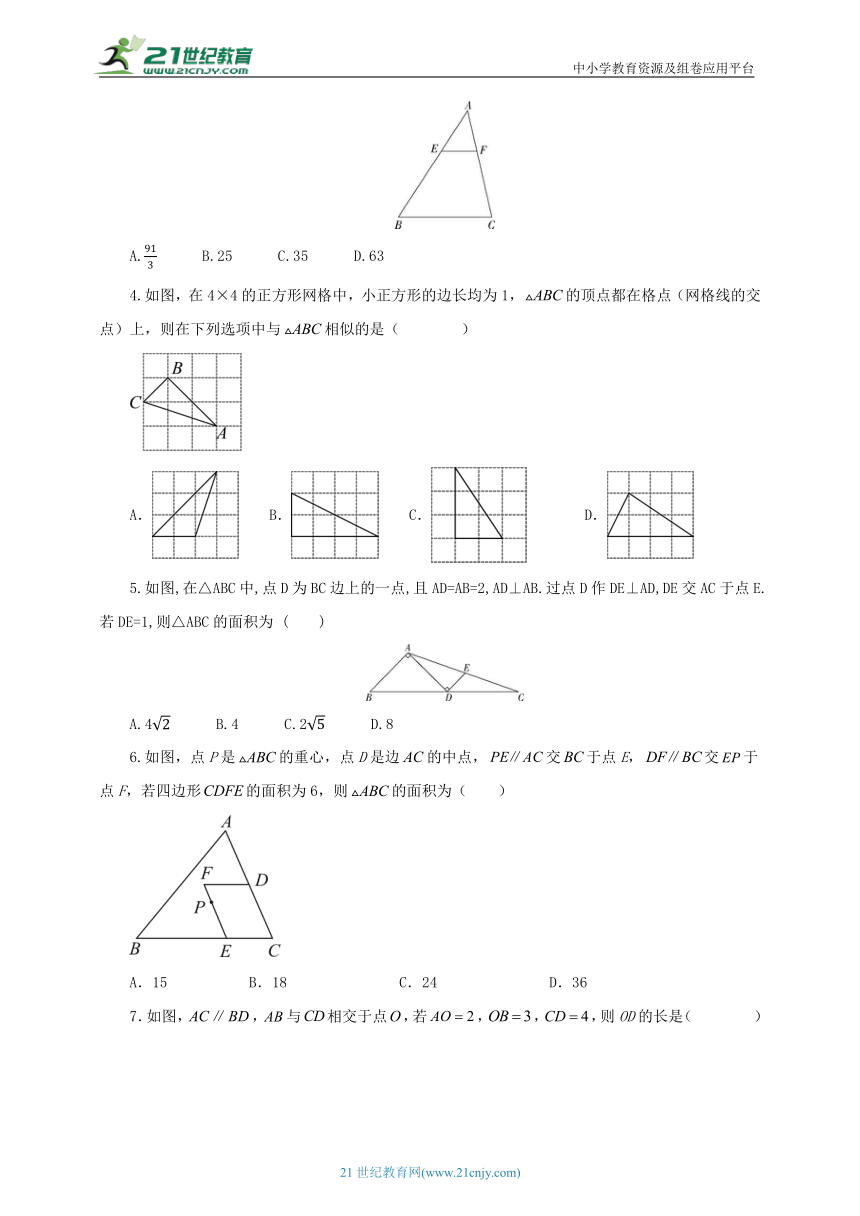
3.如图,在△ABC中,EF∥BC,=,四边形BCFE的面积为21,则△ABC的面积是 ( )
A. B.25 C.35 D.63
4.如图,在4×4的正方形网格中,小正方形的边长均为1,的顶点都在格点(网格线的交点)上,则在下列选项中与相似的是( )
A. B. C. D.
5.如图,在△ABC中,点D为BC边上的一点,且AD=AB=2,AD⊥AB.过点D作DE⊥AD,DE交AC于点E.若DE=1,则△ABC的面积为 ( )
A.4 B.4 C.2 D.8
6.如图,点P是的重心,点D是边的中点,交于点E,交于点F,若四边形的面积为6,则的面积为( )
A.15 B.18 C.24 D.36
7.如图,,与相交于点,若,,,则OD的长是( )
A.3 B. C.2 D.
8.如图,的顶点均在正方形网格的格点上,下列阴影部分的三角形与相似的是( )
A. B. C. D.
9.如图,中,,,,D为的中点,若动点E以的速度从A点出发,沿着A→B的方向运动,设E点的运动时间为t秒(),连接,当以B、D、E为顶点的三角形与相似时,t的值为( )
A.2 B.2.5或3.5 C.2或3.5 D.2或2.5
10.如图,在平面直角坐标系中,已知,,点与坐标原点关于直线对称.将沿轴向右平移,当线段扫过的面积为20时,此时点的对应点的坐标为( )
A. B. C. D.
填空题
11. 已知△ABC∽△DEF,且面积比为1∶9,若△ABC的周长为8 cm,则△DEF的周长是 cm.
12.如图,在中,是中线,G是重心,,交于D.若,则 .
13.如图,已知每个小方格的边长均为1,则△ABC与△CDE的周长比为 .
14.如图,在中,分别平分与,延长交于点D,连接,作,垂足为E,若,,,则的面积为 .
15.如图,若点,,,,,,,,都是方格纸中的格点,为使,则点应是,,,四点中的 点.
三、解答题
16.如图,G为的重心,,求的值.
17.如图,在△ABC中,点D、E、F分别在AB、BC、AC边上,DE∥AC,EF∥AB.
(1)求证:△BDE∽△EFC;
(2)若=,且S△DBE=2,求△ABC的面积.
18.如图所示,中,,,,点从点出发,以的速度沿边向终点运动,过点作于点,并作关于直线对称的,设点的运动时间为,与的重叠面积为.
(1)当点在边上时, ______(用含的代数式表示).
(2)当点与点重合时,求的值;
(3)求与的函数关系式,并直接写出自变量的取值范围.
(一)课后反思:
本节课我学会了:
本节课存在的问题:
把本节课所学知识画出思维导图
参考答案
【答案】 A
【分析】∵两个相似三角形的面积比为1∶9,∴它们对应角的平分线之比为1∶=1∶3=.故选A.
2.D
【分析】根据平行四边形的性质得到,得到,根据相似三角形的性质计算即可.
【详解】解:四边形是平行四边形,
,,
,
∴,
,
∴,
故选:D.
【点睛】本题考查的是相似三角形的性质、平行四边形的性质,掌握相似三角形的面积比等于相似比的平方是解题的关键.
3.【答案】 B
【分析】∵EF∥BC,∴△AEF∽△ABC,∴===,∴S△AEF=S△ABC.∵S四边形BCFE=S△ABC-S△AEF=21,即S△ABC=21,∴S△ABC=25.故选B.
4.B
【分析】可利用正方形的边把对应的线段表示出来,利用三边对应成比例两个三角形相似,分别计算各边的长度即可解题.
【详解】解:由网格的特点知,、都是正方形的角平分线,
则,,
显然,选项A、D都不是直角三角形,不符合题意;
选项B中,夹直角的两边的比为,符合题意;
选项C中,夹直角的两边的比为,不符合题意;
故选:B.
【点睛】此题考查了勾股定理在直角三角形中的运用,有一角相等及夹这角的两边对应成比例判定三角形相似的方法,本题中根据网格的特点求得,是解题的关键.
【答案】 B
【分析】∵AB⊥AD,DE⊥AD,
∴AB∥DE,
∴△CDE∽△CBA.
∴===,
∴S△CDE=S△CBA,∴S四边形ABDE=S△CBA.
∵S四边形ABDE=S△ABD+S△ADE=AB·AD+AD·DE=×2×2+×2×1=3,∴S△CBA=S四边形ABDE=×3=4.
故选B.
6.B
【分析】连接,根据三角形重心的性质可知:P在上,由三角形中线平分三角形的面积可知:,证明和,根据相似三角形面积的比等于相似比的平方可解答.
【详解】解:如图,连接,
点P是的重心,点D是边的中点,P在上,
,
,
,
,
,
,
,
设的面积为m,则的面积为,的面积为,
四边形的面积为6,
,
,
的面积为9,
的面积是18.
故选:B.
【点睛】本题主要考查了三角形重心的性质,相似三角形的判定与性质,难度适中,准确作出辅助线是解题的关键.
7.B
【分析】根据可得,根据相似三角形的性质以及已知条件,可得,进而即可求解.
【详解】解:∵
∴
∴
∵,,
∴
∵,
∴
故选:B.
【点睛】本题考查了相似三角形的性质与判定,熟练掌握相似三角形的性质与判定是解题的关键.
8.A
【分析】应用两三角形相似判定定理,三边对应成比例,分别对各选项进行分析即可得出答案.
【详解】解:在中,
,,,
A、三边分别为,,,则,故与相似,符合题意;
B、三边分别为,,,则,故与不相似,不符合题意;
C、三边分别为,,,则,故与不相似,不符合题意;
D、三边分别为,,,则,故与不相似,不符合题意;
故选:A.
【点睛】本题考查三角形相似判定定理以及勾股定理,是基础知识要熟练掌握.
9.C
【分析】求出,分两种情况:①当时,,,得出,即可得出;②当时,证出,得出,因此,得出,;即可得出结果.
【详解】解:∵,,
∴,
∴,
分两种情况:
①当时,
,,
∵D为的中点,
∴,E为的中点,,
∴;
②当时,
∵,
∴,
∴,
∴,
∴,
∴;
综上所述:当以B、D、E为顶点的三角形与相似时,t的值为2或3.5;
故选:C.
【点睛】本题考查了相似三角形的判定、平行线的性质、含30度角的直角三角形的性质等知识;熟记相似三角形的判定方法是解决问题的关键,注意分类讨论.
10.B
【分析】连接AA1、BB1,过C点作CE⊥x轴于E点,过B点作BD⊥CE,交EC的延长线于点D,根据A(-2,0)、B(0,4),OA=2,OB=4,进而得到AC=2,BC=4,再证Rt△DBC∽Rt△ECA,得到,设AE=x,则有CD=2x,OE=AO+AE=2+x,在Rt△ACE中,,即有,解方程求出x,即可求出AE,则C点坐标可求,再根据AB扫过的面积为20,求得,可知△ABC向右平移了5个单位,则问题得解.
【详解】平移后的效果如图,连接AA1、BB1,过C点作CE⊥x轴于E点,过B点作BD⊥CE,交EC的延长线于点D,
根据平移的性质可知AA1=BB1,且,
即有四边形是平行四边形.
∵CE⊥x轴,BD⊥CE,
∴∠D=∠CEA=90°,
根据对称的性质可知△AOB≌△ACB,
∴∠ACB=∠AOB=90°,AO=AC,OB=BC,
∵A(-2,0)、B(0,4),
∴OA=2,OB=4,
∴AO=AC=2,OB=BC=4,
∵∠ACB=90°=∠D,
∴∠DCB+∠ACE=90°,∠DCB+∠DBC=90°,
∴∠ACE=∠CBD,
∴Rt△DBC∽Rt△ECA,
∴,
设AE=x,则有CD=2x,
∴OE=AO+AE=2+x,
∵∠D=∠CEA=90°=∠AOB,
∴四边形OBDE是矩形,
∴BD=OE,即BD=2+x,
∵,
∴,
∴在Rt△ACE中,,
∴有,解得,(负值舍去),
∴,
∴,,
∴C点坐标为,
根据平移的性质可知直线AB扫过的图形为是平行四边形,
∴根据题意有,
∵,
∴,
∴,
∴可知△ABC向右平移了5个单位,
∴C也向右平移了5个单位才得到C1,
∴即,
∴C1点坐标为,
故选:B.
【点睛】本题考查了平移的性质、平行四边形的判定与性质、勾股定理、相似三角形的判定与性质、一元二次方程的应用等知识,求出C点的坐标是解答本题的关键.
11.【答案】 24
【解析】 ∵△ABC∽△DEF,且面积比为1∶9,∴△ABC与△DEF的相似比为1∶3,∴△ABC与△DEF的周长比为1∶3,∵△ABC的周长为8 cm,∴△DEF的周长是3×8=24(cm).
12. 2
【分析】先求解,证明,可得,由三角形的重心的性质可得,再建立方程即可.
【详解】解:∵是中线,,
∴,
∵,
∴,
∴,
∵G是的重心,
∴,
∴,
∴;
故答案为:2.
【点睛】本题考查的是三角形的中线的性质,三角形的重心的性质,相似三角形的判定与性质,熟记三角形的重心的性质是解本题的关键.
13.【答案】 2∶1
【解析】 由题图知AB∥DE,AB==2,DE==,∴△ABC∽△DEC,∴△ABC的周长∶△CDE的周长=AB∶DE=2∶=2∶1.
14.
【分析】过D点作交于点F,则,得到,可求出的长,利用角平分线得到,进而求出长,计算面积即可.
【详解】解:如图,过D点作交于点F,
∴,
∴,
∵
∴DF
∵
∴
∵平分
∴
∴
∴
∵
∴
故答案为:.
【点睛】本题考查相似三角形的判定和性质,等腰三角形的判定,作辅助线构造相似三角形是解题的关键.
15.
【分析】相似三角形两个角对应相等,且对应边成比例,据此解答.
【详解】解:由图知,点应位于线段的中垂线上,
所以要使,
所以只能是点,
其他点均不符合题意,
故答案为:.
【点睛】本题考查了相似三角形,熟练掌握相似三角形的判定,要注意联系实际图形进行判定.
16.24
【分析】G为的重心,判断出点是边的中点,即可判断出;即可得出,求出即可得出结论.
【详解】解: 点为的重心,
,
∴
,
,
点为的重心,
点是边的中点,
;
点为的重心,
,
,
,
∴.
【点睛】此题主要考查了三角形的重心的性质和应用以及相似,要熟练掌握,解答此题的关键是要明确:重心就是三条中线的交点,重心到顶点的距离与重心到对边中点的距离之比为.
17.【解析】 (1)证明:∵DE∥AC,
∴∠BED=∠C.
∵EF∥AB,
∴∠B=∠CEF,
∴△BDE∽△EFC.
(2)∵DE∥AC,EF∥AB,
∴四边形ADEF为平行四边形,
∴AF=DE.
∵=,
∴=,
∵DE∥AC,
∴△BDE∽△BAC,
∴==,
∴S△ABC=9S△BDE=9×2=18.
18.(1)
(2)
(3)
【分析】(1)由勾股定理得出,由题意得出,通过证明,得出,即,进行计算即可得到答案;
(2)由(1)知:,可得,即,,由题意得出,即可求得答案;
(3)分三种情况:当时,重叠部分为,且;当时,重叠部分为四边形,利用计算即可得到答案;当时,重叠部分为直角三角形,运用相似三角形的性质即可求得答案.
【详解】(1)解:中,,,,
,
点从点出发,以的速度沿边向终点运动,
当点在边上时,,
,,
,
,
,
,即,
解得:,
故答案为:;
(2)解:当点与点重合时,如图①,
,
,
由(1)知:,
,即,
,
由题意知:当时,,
,
解得,
故当点与点重合时,的值为;
(3)解:当时,如图②,,
,
由(1)知:,,
,即,
,,
,
与关于直线对称,
,
;
当时,如图③,设交于,取的中点,作交于,连接,
,
则,
,
,,
,
,
,,
,
,
,
,
,
,
,
,
;
当时,如图④,过点作于,
,
,,
,
,即,
,,
,
,
,
,,
,
,
,即,
,即,
综上所述,与的函数关系式为.
【点睛】本题主要考查了相似三角形的判定与性质、勾股定理、三角形面积等知识,解题的关键是灵活运用分类讨论思想解决问题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
22.3 相似三角形的性质 导学案
(一)学习目标:
1.明确相似三角形中对应线段与相似比的关系.
2.掌握相似三角形的周长比等于相似比、面积比等于相似比的平方及其在实际中的应用.
(二)学习重难点
重点:明确相似三角形中对应线段与相似比的关系.
难点:相似三角形的性质定理解决简单的实际问题.
阅读课本,识记知识:
性质1:相似三角形的对应角相等,对应边对应成比例.
性质2:相似三角形中的重要线段的比等于相似比.
相似三角形对应高,对应中线,对应角平分线的比都等于相似比.
注意:要特别注意“对应”两个字,在应用时,要注意找准对应线段.
性质3:相似三角形周长的比等于相似比
如图一: ∽,则
由比例性质可得:
性质4:相似三角形面积的比等于相似比的平方
如图二,∽,则分别作出与的高和,则
注意:相似三角形的性质是通过比例线段的性质推证出来的.
射影定理
射影定理:如图,Rt△ABC,∠C=90 ,CD⊥AB
则,1.CD2=AD·BD
2.BC2=BD·AB
AC2=AD·AB
很容易推出:.
AC·BC=AB·CD.
BC2+AC2=AB2.
.
AC+BC<AB+CD.
用图中小写字母a、b、c、p、q、h(常称为勾股六线段)表达以上关系:
① h2=pq ;② a2=pc ;③ b2=qc ;④ ;⑤ ab=ch ;
⑥ a2+b2=c2 ;⑦ ;⑧ a+b<c+h;⑨ c=p+q.
利用上述关系式, “知二可求四” ,即在a、b、c、p、q、h这六个量中,已知两个量就可求出其余四个量来。同学们自己可任意设出两个量,练习求另外四个量(在设的时候,要注意构成直角三角形的基本条件:斜边大于直角边
【例1】如图,在中,中线相交于点G,下列说法错误的是( )
A.点G为的重心 B.
C.当为等边三角形时, D.
【答案】D
【分析】根据三角形的重心性质可判断选项A、B;根据等边三角形的性质得到,可判断选项C;根据三角形的中线将三角形的面积平分可判断选项D.
【详解】解:A、∵的中线相交于点G,
∴点G为的重心,故选项A正确,不符合题意;
B、∵点G 为的重心,
∴,即,故选项B正确,不符合题意;
C、∵为等边三角形,
∴,
∵,,
∴,,
∴,故选项C正确,不符合题意;
D、∵,
∴,则,
∴,故选项D错误,符合题意,
故选:D.
【点睛】本题考查三角形的重心性质、等边三角形的性质、三角形的中线性质,解答的关键是熟练掌握三角形的中线性质和重心性质:三角形的重心到顶点的距离与重心到对边中点的距离之比为.
【例2】 《笛卡尔几何学》一书中引入单位线段1来表示线段的乘除.如图,已知,则,若规定为单位线段1,则,若规定为单位线段1,则为( )
A. B. C. D.
【答案】C
【分析】由,可得,根据比例的性质可得,即,由于规定为单位线段1,则,即可解答.
【详解】解:∵,
∴,
∴,
即,
∴,
∵规定为单位线段1,
∴.
故选:C.
【点睛】本题考查相似三角形的性质,比例的性质,读懂题意,正确使用比例的性质是解题的关键.
选择题
1.若两个相似三角形的面积之比为1∶9,则它们对应角的平分线之比为 ( )
A. B.3 C. D.3
2.如图,在中,为上一点,连接,,且与相交于点,,则( )
A. B. C. D.
3.如图,在△ABC中,EF∥BC,=,四边形BCFE的面积为21,则△ABC的面积是 ( )
A. B.25 C.35 D.63
4.如图,在4×4的正方形网格中,小正方形的边长均为1,的顶点都在格点(网格线的交点)上,则在下列选项中与相似的是( )
A. B. C. D.
5.如图,在△ABC中,点D为BC边上的一点,且AD=AB=2,AD⊥AB.过点D作DE⊥AD,DE交AC于点E.若DE=1,则△ABC的面积为 ( )
A.4 B.4 C.2 D.8
6.如图,点P是的重心,点D是边的中点,交于点E,交于点F,若四边形的面积为6,则的面积为( )
A.15 B.18 C.24 D.36
7.如图,,与相交于点,若,,,则OD的长是( )
A.3 B. C.2 D.
8.如图,的顶点均在正方形网格的格点上,下列阴影部分的三角形与相似的是( )
A. B. C. D.
9.如图,中,,,,D为的中点,若动点E以的速度从A点出发,沿着A→B的方向运动,设E点的运动时间为t秒(),连接,当以B、D、E为顶点的三角形与相似时,t的值为( )
A.2 B.2.5或3.5 C.2或3.5 D.2或2.5
10.如图,在平面直角坐标系中,已知,,点与坐标原点关于直线对称.将沿轴向右平移,当线段扫过的面积为20时,此时点的对应点的坐标为( )
A. B. C. D.
填空题
11. 已知△ABC∽△DEF,且面积比为1∶9,若△ABC的周长为8 cm,则△DEF的周长是 cm.
12.如图,在中,是中线,G是重心,,交于D.若,则 .
13.如图,已知每个小方格的边长均为1,则△ABC与△CDE的周长比为 .
14.如图,在中,分别平分与,延长交于点D,连接,作,垂足为E,若,,,则的面积为 .
15.如图,若点,,,,,,,,都是方格纸中的格点,为使,则点应是,,,四点中的 点.
三、解答题
16.如图,G为的重心,,求的值.
17.如图,在△ABC中,点D、E、F分别在AB、BC、AC边上,DE∥AC,EF∥AB.
(1)求证:△BDE∽△EFC;
(2)若=,且S△DBE=2,求△ABC的面积.
18.如图所示,中,,,,点从点出发,以的速度沿边向终点运动,过点作于点,并作关于直线对称的,设点的运动时间为,与的重叠面积为.
(1)当点在边上时, ______(用含的代数式表示).
(2)当点与点重合时,求的值;
(3)求与的函数关系式,并直接写出自变量的取值范围.
(一)课后反思:
本节课我学会了:
本节课存在的问题:
把本节课所学知识画出思维导图
参考答案
【答案】 A
【分析】∵两个相似三角形的面积比为1∶9,∴它们对应角的平分线之比为1∶=1∶3=.故选A.
2.D
【分析】根据平行四边形的性质得到,得到,根据相似三角形的性质计算即可.
【详解】解:四边形是平行四边形,
,,
,
∴,
,
∴,
故选:D.
【点睛】本题考查的是相似三角形的性质、平行四边形的性质,掌握相似三角形的面积比等于相似比的平方是解题的关键.
3.【答案】 B
【分析】∵EF∥BC,∴△AEF∽△ABC,∴===,∴S△AEF=S△ABC.∵S四边形BCFE=S△ABC-S△AEF=21,即S△ABC=21,∴S△ABC=25.故选B.
4.B
【分析】可利用正方形的边把对应的线段表示出来,利用三边对应成比例两个三角形相似,分别计算各边的长度即可解题.
【详解】解:由网格的特点知,、都是正方形的角平分线,
则,,
显然,选项A、D都不是直角三角形,不符合题意;
选项B中,夹直角的两边的比为,符合题意;
选项C中,夹直角的两边的比为,不符合题意;
故选:B.
【点睛】此题考查了勾股定理在直角三角形中的运用,有一角相等及夹这角的两边对应成比例判定三角形相似的方法,本题中根据网格的特点求得,是解题的关键.
【答案】 B
【分析】∵AB⊥AD,DE⊥AD,
∴AB∥DE,
∴△CDE∽△CBA.
∴===,
∴S△CDE=S△CBA,∴S四边形ABDE=S△CBA.
∵S四边形ABDE=S△ABD+S△ADE=AB·AD+AD·DE=×2×2+×2×1=3,∴S△CBA=S四边形ABDE=×3=4.
故选B.
6.B
【分析】连接,根据三角形重心的性质可知:P在上,由三角形中线平分三角形的面积可知:,证明和,根据相似三角形面积的比等于相似比的平方可解答.
【详解】解:如图,连接,
点P是的重心,点D是边的中点,P在上,
,
,
,
,
,
,
,
设的面积为m,则的面积为,的面积为,
四边形的面积为6,
,
,
的面积为9,
的面积是18.
故选:B.
【点睛】本题主要考查了三角形重心的性质,相似三角形的判定与性质,难度适中,准确作出辅助线是解题的关键.
7.B
【分析】根据可得,根据相似三角形的性质以及已知条件,可得,进而即可求解.
【详解】解:∵
∴
∴
∵,,
∴
∵,
∴
故选:B.
【点睛】本题考查了相似三角形的性质与判定,熟练掌握相似三角形的性质与判定是解题的关键.
8.A
【分析】应用两三角形相似判定定理,三边对应成比例,分别对各选项进行分析即可得出答案.
【详解】解:在中,
,,,
A、三边分别为,,,则,故与相似,符合题意;
B、三边分别为,,,则,故与不相似,不符合题意;
C、三边分别为,,,则,故与不相似,不符合题意;
D、三边分别为,,,则,故与不相似,不符合题意;
故选:A.
【点睛】本题考查三角形相似判定定理以及勾股定理,是基础知识要熟练掌握.
9.C
【分析】求出,分两种情况:①当时,,,得出,即可得出;②当时,证出,得出,因此,得出,;即可得出结果.
【详解】解:∵,,
∴,
∴,
分两种情况:
①当时,
,,
∵D为的中点,
∴,E为的中点,,
∴;
②当时,
∵,
∴,
∴,
∴,
∴,
∴;
综上所述:当以B、D、E为顶点的三角形与相似时,t的值为2或3.5;
故选:C.
【点睛】本题考查了相似三角形的判定、平行线的性质、含30度角的直角三角形的性质等知识;熟记相似三角形的判定方法是解决问题的关键,注意分类讨论.
10.B
【分析】连接AA1、BB1,过C点作CE⊥x轴于E点,过B点作BD⊥CE,交EC的延长线于点D,根据A(-2,0)、B(0,4),OA=2,OB=4,进而得到AC=2,BC=4,再证Rt△DBC∽Rt△ECA,得到,设AE=x,则有CD=2x,OE=AO+AE=2+x,在Rt△ACE中,,即有,解方程求出x,即可求出AE,则C点坐标可求,再根据AB扫过的面积为20,求得,可知△ABC向右平移了5个单位,则问题得解.
【详解】平移后的效果如图,连接AA1、BB1,过C点作CE⊥x轴于E点,过B点作BD⊥CE,交EC的延长线于点D,
根据平移的性质可知AA1=BB1,且,
即有四边形是平行四边形.
∵CE⊥x轴,BD⊥CE,
∴∠D=∠CEA=90°,
根据对称的性质可知△AOB≌△ACB,
∴∠ACB=∠AOB=90°,AO=AC,OB=BC,
∵A(-2,0)、B(0,4),
∴OA=2,OB=4,
∴AO=AC=2,OB=BC=4,
∵∠ACB=90°=∠D,
∴∠DCB+∠ACE=90°,∠DCB+∠DBC=90°,
∴∠ACE=∠CBD,
∴Rt△DBC∽Rt△ECA,
∴,
设AE=x,则有CD=2x,
∴OE=AO+AE=2+x,
∵∠D=∠CEA=90°=∠AOB,
∴四边形OBDE是矩形,
∴BD=OE,即BD=2+x,
∵,
∴,
∴在Rt△ACE中,,
∴有,解得,(负值舍去),
∴,
∴,,
∴C点坐标为,
根据平移的性质可知直线AB扫过的图形为是平行四边形,
∴根据题意有,
∵,
∴,
∴,
∴可知△ABC向右平移了5个单位,
∴C也向右平移了5个单位才得到C1,
∴即,
∴C1点坐标为,
故选:B.
【点睛】本题考查了平移的性质、平行四边形的判定与性质、勾股定理、相似三角形的判定与性质、一元二次方程的应用等知识,求出C点的坐标是解答本题的关键.
11.【答案】 24
【解析】 ∵△ABC∽△DEF,且面积比为1∶9,∴△ABC与△DEF的相似比为1∶3,∴△ABC与△DEF的周长比为1∶3,∵△ABC的周长为8 cm,∴△DEF的周长是3×8=24(cm).
12. 2
【分析】先求解,证明,可得,由三角形的重心的性质可得,再建立方程即可.
【详解】解:∵是中线,,
∴,
∵,
∴,
∴,
∵G是的重心,
∴,
∴,
∴;
故答案为:2.
【点睛】本题考查的是三角形的中线的性质,三角形的重心的性质,相似三角形的判定与性质,熟记三角形的重心的性质是解本题的关键.
13.【答案】 2∶1
【解析】 由题图知AB∥DE,AB==2,DE==,∴△ABC∽△DEC,∴△ABC的周长∶△CDE的周长=AB∶DE=2∶=2∶1.
14.
【分析】过D点作交于点F,则,得到,可求出的长,利用角平分线得到,进而求出长,计算面积即可.
【详解】解:如图,过D点作交于点F,
∴,
∴,
∵
∴DF
∵
∴
∵平分
∴
∴
∴
∵
∴
故答案为:.
【点睛】本题考查相似三角形的判定和性质,等腰三角形的判定,作辅助线构造相似三角形是解题的关键.
15.
【分析】相似三角形两个角对应相等,且对应边成比例,据此解答.
【详解】解:由图知,点应位于线段的中垂线上,
所以要使,
所以只能是点,
其他点均不符合题意,
故答案为:.
【点睛】本题考查了相似三角形,熟练掌握相似三角形的判定,要注意联系实际图形进行判定.
16.24
【分析】G为的重心,判断出点是边的中点,即可判断出;即可得出,求出即可得出结论.
【详解】解: 点为的重心,
,
∴
,
,
点为的重心,
点是边的中点,
;
点为的重心,
,
,
,
∴.
【点睛】此题主要考查了三角形的重心的性质和应用以及相似,要熟练掌握,解答此题的关键是要明确:重心就是三条中线的交点,重心到顶点的距离与重心到对边中点的距离之比为.
17.【解析】 (1)证明:∵DE∥AC,
∴∠BED=∠C.
∵EF∥AB,
∴∠B=∠CEF,
∴△BDE∽△EFC.
(2)∵DE∥AC,EF∥AB,
∴四边形ADEF为平行四边形,
∴AF=DE.
∵=,
∴=,
∵DE∥AC,
∴△BDE∽△BAC,
∴==,
∴S△ABC=9S△BDE=9×2=18.
18.(1)
(2)
(3)
【分析】(1)由勾股定理得出,由题意得出,通过证明,得出,即,进行计算即可得到答案;
(2)由(1)知:,可得,即,,由题意得出,即可求得答案;
(3)分三种情况:当时,重叠部分为,且;当时,重叠部分为四边形,利用计算即可得到答案;当时,重叠部分为直角三角形,运用相似三角形的性质即可求得答案.
【详解】(1)解:中,,,,
,
点从点出发,以的速度沿边向终点运动,
当点在边上时,,
,,
,
,
,
,即,
解得:,
故答案为:;
(2)解:当点与点重合时,如图①,
,
,
由(1)知:,
,即,
,
由题意知:当时,,
,
解得,
故当点与点重合时,的值为;
(3)解:当时,如图②,,
,
由(1)知:,,
,即,
,,
,
与关于直线对称,
,
;
当时,如图③,设交于,取的中点,作交于,连接,
,
则,
,
,,
,
,
,,
,
,
,
,
,
,
,
,
;
当时,如图④,过点作于,
,
,,
,
,即,
,,
,
,
,
,,
,
,
,即,
,即,
综上所述,与的函数关系式为.
【点睛】本题主要考查了相似三角形的判定与性质、勾股定理、三角形面积等知识,解题的关键是灵活运用分类讨论思想解决问题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
