九年级数学上册 22.4 图形的位似变换 导学案(知识清单 典型例题 巩固提升)
文档属性
| 名称 | 九年级数学上册 22.4 图形的位似变换 导学案(知识清单 典型例题 巩固提升) |

|
|
| 格式 | docx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-08 13:19:26 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
22.4 图形的位似变换 导学案
(一)学习目标:
1.知道位似图形的相关概念,会利用位似变换将一个图形放大或缩小.
2.知道位似与相似的联系与区别.
3.会在网格图中作位似图形,能找出位似图形的位似中心。
(二)学习重难点:
重点:作位似图形.
难点:位似变换与其他图形变换的综合问题.
阅读课本,识记知识:
1.位似变换
(1)位似图形的定义:
如果两个图形不仅是相似图形,而且对应顶点的连线相交于一点,对应边互相平行,那么这样的两个图形叫做位似图形,这个点叫做位似中心.
注意:①两个图形必须是相似形;
②对应点的连线都经过同一点;
③对应边平行.
(2)位似图形与坐标
在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或﹣k.
2.作图-位似变换
(1)画位似图形的一般步骤为:
①确定位似中心;②分别连接并延长位似中心和能代表原图的关键点;③根据位似比,确定能代表所作的位似图形的关键点;④顺次连接上述各点,得到放大或缩小的图形.
借助橡皮筋、方格纸、格点图等简易工具可将图形放大或缩小,借助计算机也很好地将一个图形放大或缩小.
注意:①画一个图形的位似图形时,位似中心的选择是任意的,这个点可以在图形的内部或外部或在图形上,对于具体问题要考虑画图方便且符合要求.②由于位似中心选择的任意性,因此作已知图形的位似图形的结果是不唯一的.
【例1】如图,与位似,点为位似中心,位似比为,若的周长为6,则的周长是( )
A.16 B.9 C.6 D.4
【答案】D
【分析】根据位似变换的定义、相似三角形的性质计算即可.
【详解】解:和是位似图形,位似比为,
和的相似比为,
的周长的周长,
故选:D.
【点睛】此题主要考查了位似图形的性质,熟练掌握位似图形的性质是解题关键.
【例2】如图,与位似,点O为位似中心,若的周长等于周长的.,则的长度为( )
A.4 B.6 C.8 D.10
【答案】C
【分析】根据位似变换的概念得到,根据周长之比得到相似比,继而求解.
【详解】解:∵与位似,
∴,
∵的周长等于周长的,
∴相似比为,
∵,
∴,
故选C.
【点睛】本题考查的是位似变换、相似三角形的性质,掌握相似三角形的周长比等于相似比是解题的关键.
选择题
1.下列各组图形中的两个三角形均满足△ABC∽△DEF,这两个三角形不是位似图形的是 ( )
A B C D
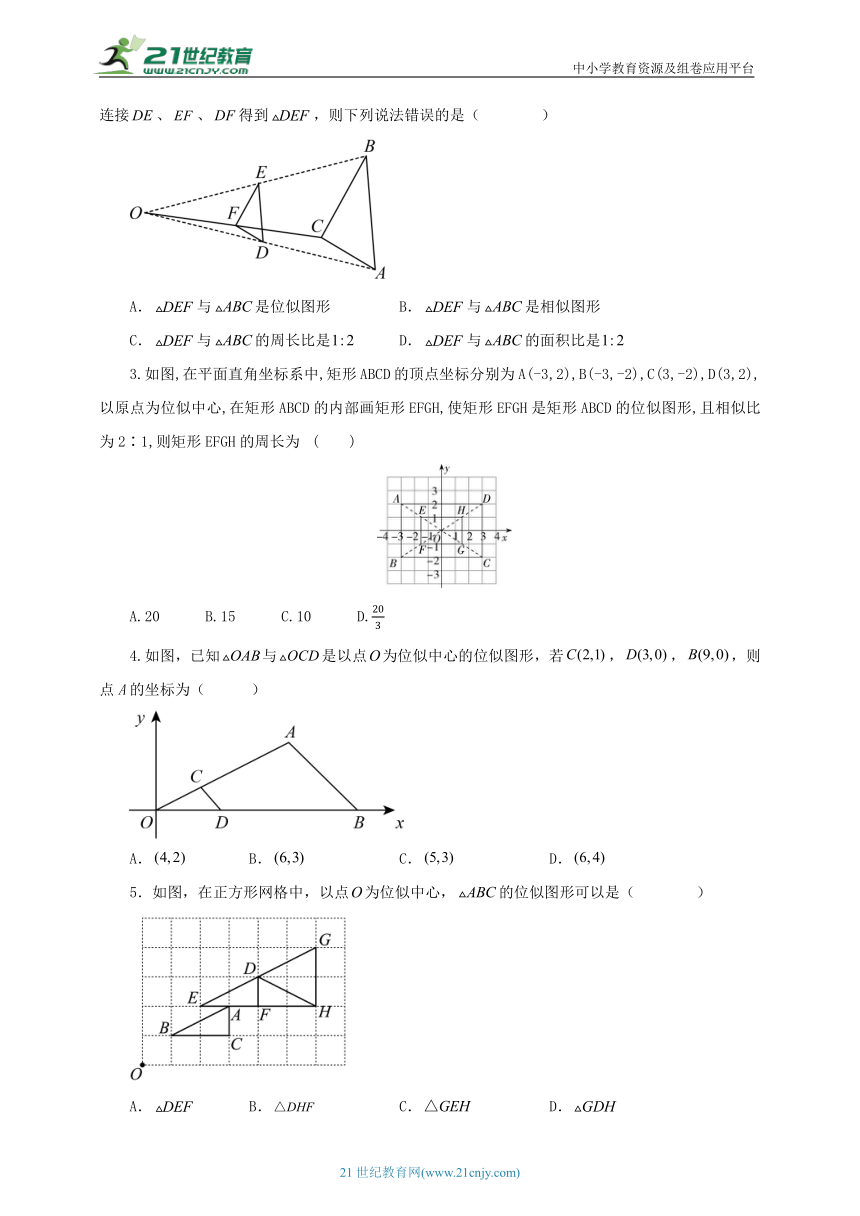
2.如图,在外任取一点,连接、、,并分别取它们的中点、、,顺次连接、、得到,则下列说法错误的是( )
A.与是位似图形 B.与是相似图形
C.与的周长比是 D.与的面积比是
3.如图,在平面直角坐标系中,矩形ABCD的顶点坐标分别为A(-3,2),B(-3,-2),C(3,-2),D(3,2),以原点为位似中心,在矩形ABCD的内部画矩形EFGH,使矩形EFGH是矩形ABCD的位似图形,且相似比为2∶1,则矩形EFGH的周长为 ( )
A.20 B.15 C.10 D.
4.如图,已知与是以点为位似中心的位似图形,若,,,则点A的坐标为( )
A. B. C. D.
5.如图,在正方形网格中,以点为位似中心,的位似图形可以是( )
A. B. C. D.
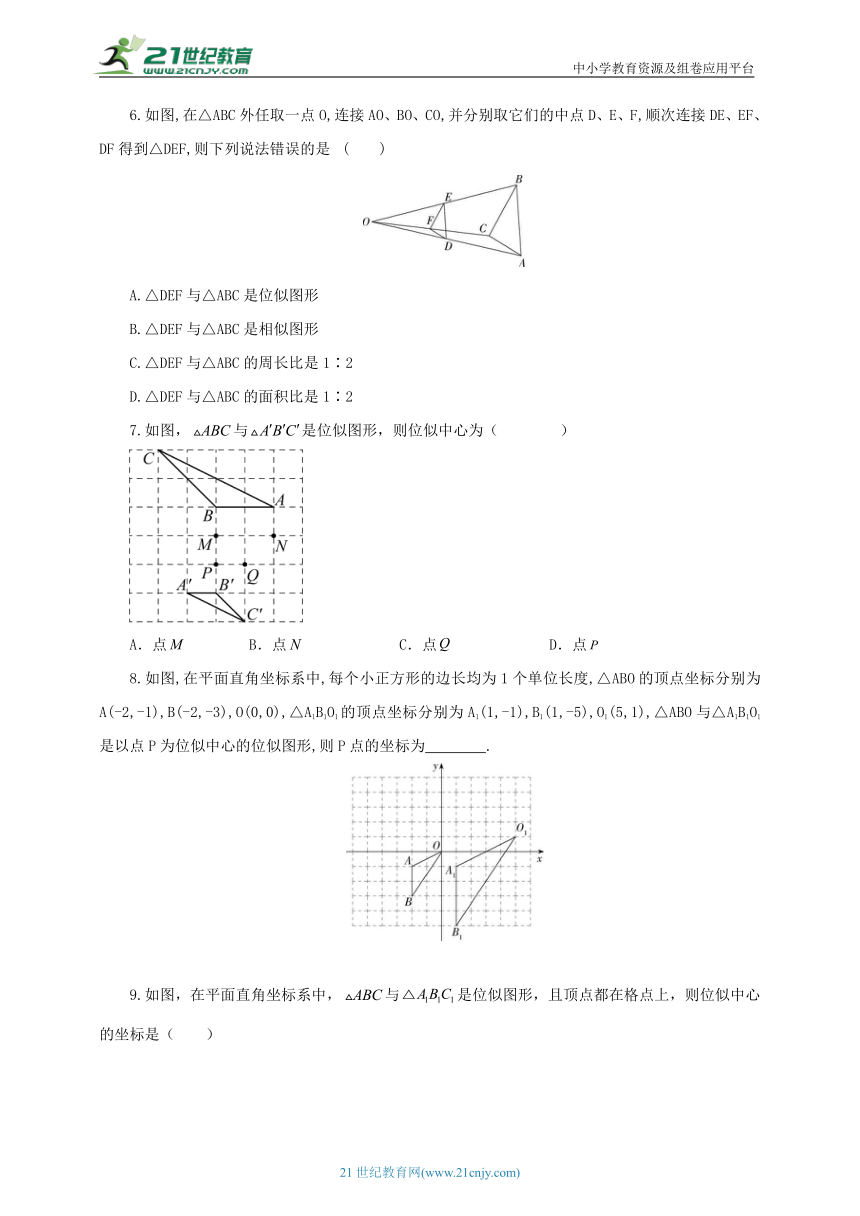
6.如图,在△ABC外任取一点O,连接AO、BO、CO,并分别取它们的中点D、E、F,顺次连接DE、EF、DF得到△DEF,则下列说法错误的是 ( )
A.△DEF与△ABC是位似图形
B.△DEF与△ABC是相似图形
C.△DEF与△ABC的周长比是1∶2
D.△DEF与△ABC的面积比是1∶2
7.如图,与是位似图形,则位似中心为( )
A.点 B.点 C.点 D.点
8.如图,在平面直角坐标系中,每个小正方形的边长均为1个单位长度,△ABO的顶点坐标分别为A(-2,-1),B(-2,-3),O(0,0),△A1B1O1的顶点坐标分别为A1(1,-1),B1(1,-5),O1(5,1),△ABO与△A1B1O1是以点P为位似中心的位似图形,则P点的坐标为 .
9.如图,在平面直角坐标系中,与是位似图形,且顶点都在格点上,则位似中心的坐标是( )
A. B. C. D.
10.如图,在直角坐标系中,与是位似图形,已知点,则位似中心的坐标是( )
A. B. C. D.
填空题
11.如图,在平面直角坐标系中,阴影所示的两个正方形是位似图形,若位似中心在两个正方形之间,则位似中心的坐标为 .
12.如图,△A'B'C'与△ABC是位似图形,点O为位似中心,若OA'=AA',则△A'B'C'与△ABC的面积比为 .
13.如图,与位似,点为位似中心,若,的周长为4,则的周长为 .
14.由12个有公共顶点O的直角三角形拼成如图所示的图形,.若,则图中与位似的三角形中,边对应边的长为 .
15.如图,在平面直角坐标系中,点、的坐标分别为、,点、的坐标分别为、.若线段和是位似图形,且位似中心在轴上,则位似中心的坐标为 .
三、解答题
16.如图,已知图中的每个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点,若与是位似图形且顶点均在格点上.
(1)在图中画出位似中心的位置,并写出位似中心的坐标;
(2)与的位似比为__________,面积比为__________.
17.如图,在平面直角坐标系中,△ABC和△A1B1C1关于点E成中心对称,
(1)在图中标出点E,且点E的坐标为 ;
(2)点P(a,b)是△ABC边AB上一点,△ABC经过平移后点P的对应点P'的坐标为(a-6,b+2),请画出上述平移后的△A2B2C2,此时A2的坐标为 ,C2的坐标为 ;
(3)若△A1B1C1和△A2B2C2关于点F成位似三角形,则点F的坐标为 .
18.如图,图中的小方格都是边长为的正方形,与是关于点为位似中心的位似图形,它们的顶点都在小正方形的顶点上.
(1)画出位似中心点;
(2)求出与的位似比;
(3)以点为位似中心,再画一个,使它与的位似比等于.
(一)课后反思:
本节课我学会了:
本节课存在的问题:
把本节课所学知识画出思维导图
参考答案
【答案】 B
【分析】根据位似图形的概念,A、C、D三个图形中的两个三角形都是位似图形,B中的两个三角形不符合位似图形的概念,故不是位似图形.故选B.
2.【答案】C
【分析】根据位似图形的性质得出与是位似图形,根据位似图形一定是相似图形得出与是相似图形,再根据周长比等于位似比以及根据面积比等于相似比的平方即可解答.
【详解】解:根据位似性质可得:
A、与是位似图形,故A选项正确,不符合题意;
B、与是相似图形,故B选项正确,不符合题意;
C、∵点D,E,F,为中点,
∴将的三边缩小到原来的得到,
∴与的周长之比为2:1,故C选项不正确,符合题意;
D、∵面积比等于相似比的平方,
∴与的面积之比为4:1,故D选项正确,不符合题意.
故选:C.
【点睛】本题主要考查了位似图形的性质,正确的记忆位似图形性质是解决问题的关键.
3.【答案】 C
【分析】∵矩形ABCD的顶点坐标分别为A(-3,2),B(-3,-2),C(3,-2),D(3,2),∴矩形ABCD的周长为4+6+4+6=20,∵矩形ABCD与矩形EFGH的相似比为2∶1,∴矩形ABCD与矩形EFGH的周长比为2∶1,∴矩形EFGH的周长为10.故选C.
4.【答案】B
【分析】根据位似变换的性质得到,相似比为,进而求出点A的坐标.
【详解】解:∵与是以点为位似中心的位似图形,,,
∴,相似比为,
∵,
点A的坐标为,
故选:B.
【点睛】本题考查的是位似变换的概念和性质,求出与的相似比为是解题的关键.
5.【答案】C
【分析】根据位似的性质,连接并延长,观察交点即可求解.
【详解】解:如图所示,连接并延长,
∴的位似图形是.
故选:C.
【点睛】本题考查了位似图形的性质,熟练掌握位似图形的性质是解题的关键.
【答案】 D
【分析】∵AO、BO、CO的中点分别为D、E、F,∴EF=BC,DF=AC,DE=AB,∴===,∴△DEF∽△ABC,∵△DEF与△ABC的对应点连线相交于点O,∴△DEF与△ABC是位似图形,位似中心为点O,∵△DEF与△ABC的相似比为1∶2,∴△DEF与△ABC的周长比是1∶2,△DEF与△ABC的面积比是1∶4,∴D选项说法错误.故选D.
7.【答案】D
【分析】根据位似中心是位似点连线的交点判断即可.
【详解】如图,根据位似中心是位似点连线的交点,可知点P为位似中心,
故选D.
【点睛】本题考查了三角形的位似,清楚位似中心是位似点连线的交点是解题的关键.
8.答案 (-5,-1)
解析 如图,P点的坐标为(-5,-1).
9.B
【分析】根据位似图形的定义,画出位似中心,即可得出结果.
【详解】解:∵与是位似图形,
连接并延长,交于点,则点即为位似中心,如图所示:
由图可知:;
故选B.
【点睛】本题考查坐标系下求位似中心的坐标.熟练掌握位似图形的定义,确定位似中心的位置,是解题的关键.
10.B
【分析】根据位似图形的对应顶点的连线交于一点并结合网格图中的格点特征确定位似中心.
【详解】连接,并延长,交于点,点即为位似中心,如图,
∴点坐标为,
故答案为:.
【点睛】此题考查了位似变换的概念、坐标与图形性质,掌握如果两个图形不仅是相似图形,而且对应顶点的连线相交于一点,对应边互相平行,那么这样的两个图形叫做位似图形,这个点叫做位似中心是解题的关键.
11.
【分析】连接各组对应点,它们在两个正方形之间相交于点,则点为位似中心,然后写出点坐标即可.
【详解】解:如图,点为位似中心,.
故答案为:.
【点睛】本题考查位似变换:位似的两个图形不仅是相似图形,而且对应顶点的连线相交于一点,对应边互相平行(或共线),掌握位似变换的性质是解题的关键.
12. 【答案】 1∶4
【解析】 ∵△A'B'C'与△ABC是位似图形,点O为位似中心,且OA'=AA',∴S△A'B'C'∶S△ABC=(OA'∶OA)2=(1∶2)2=1∶4.
13.2
【分析】根据与位似,得出,推出,进而得出,根据相似三角形周长比等于相似比,即可求解.
【详解】解:∵与位似,
∴,
∵,
∴,
∴,
∴,
∵的周长为4,
∴的周长为2,
故答案为:2.
【点睛】本题主要考查了相似三角形那个的判定和性质,位似三角形的性质,解题的关键是掌握相似三角形周长比等于相似比.
14./
【分析】根据勾股定理和直角三角形中30度角所对的直角边等于斜边的一半,求出,,找出规律得出,即可得出答案.
【详解】解:∵在中,,,
∴,
根据勾股定理得:,
即,
解得:,
同理可得:,
…
,
∵与位似,与是对应边,
∴边对应边的长为.
故答案为:.
【点睛】本题主要考查了勾股定理,直角三角形的性质,图形规律探索,位似图形的定义,解题的关键是熟练掌握勾股定理和直角三角形中30度角所对的直角边等于斜边的一半.
15.
【分析】根据题意,位似中心在轴上,如图所示,连接与轴交于点,则点是位似中心,运用待定系数法求出直线的解析式,令,即可求解.
【详解】解:如图所示,连接与轴交于点,则点是位似中心,
∵,,
∴设所在直线的解析式为,
∴,解得,,
∴直线的解析式为,
当时,,
∴位似中心的坐标是,
故答案为:.
【点睛】本题主要考查位似与一次函数的综合,掌握位似的定义,待定系数法求一次函数解析式是解题的关键.
16.(1)见解析
(2),
【分析】(1)连接、,两线相交于点D,根据位似中心的概念、结合图形解答即可;
(2)根据,,即可得出相似比和面积比.
【详解】(1)解:如图,位似中心的坐标为:.
(2)解:∵,,
∴与的位似比为:,
与的面积比为:.
故答案为:,.
【点睛】本题考查的是位似变换的概念和性质,如果两个图形不仅是相似图形,而且对应顶点的连线所在直线相交于一点,对应边互相平行,那么这样的两个图形叫做位似图形,这个点叫做位似中心.
17.【解析】 (1)如图,连接BB1,线段BB1的中点即为点E.
∵B(1,1),B1(-1,-3),
∴E(0,-1).
(2)∵点P(a,b)是△ABC边AB上一点,△ABC经过平移后点P的对应点P'的坐标为(a-6,b+2),
∴△ABC向左平移了6个单位,向上平移了2个单位,∴△A2B2C2如图所示.
∵A(3,2),C(4,0),
∴A2(-3,4),C2(-2,2).
(3)∵连接A1A2与B1B2,它们交于点(-3,0),
∴F(-3,0).
18.(1)见解析
(2)
(3)见解析
【分析】(1)连接,分别延长三条线段交于一点O,则点O即为所求;
(2)与的位似比等于与的比,也等于与在水平线上的投影比,即,即可得到答案;
(3)按照位似图形的作图方法作即可.
【详解】(1)解:如图,点即为所求.
(2)与的位似比等于与的比,也等于与在水平线上的投影比,即.
∴与的位似比为.
(3)如图,为所求.
【点睛】此题考查了位似图形和位似图形的作图,熟练掌握位似图形的作图和性质是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
22.4 图形的位似变换 导学案
(一)学习目标:
1.知道位似图形的相关概念,会利用位似变换将一个图形放大或缩小.
2.知道位似与相似的联系与区别.
3.会在网格图中作位似图形,能找出位似图形的位似中心。
(二)学习重难点:
重点:作位似图形.
难点:位似变换与其他图形变换的综合问题.
阅读课本,识记知识:
1.位似变换
(1)位似图形的定义:
如果两个图形不仅是相似图形,而且对应顶点的连线相交于一点,对应边互相平行,那么这样的两个图形叫做位似图形,这个点叫做位似中心.
注意:①两个图形必须是相似形;
②对应点的连线都经过同一点;
③对应边平行.
(2)位似图形与坐标
在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或﹣k.
2.作图-位似变换
(1)画位似图形的一般步骤为:
①确定位似中心;②分别连接并延长位似中心和能代表原图的关键点;③根据位似比,确定能代表所作的位似图形的关键点;④顺次连接上述各点,得到放大或缩小的图形.
借助橡皮筋、方格纸、格点图等简易工具可将图形放大或缩小,借助计算机也很好地将一个图形放大或缩小.
注意:①画一个图形的位似图形时,位似中心的选择是任意的,这个点可以在图形的内部或外部或在图形上,对于具体问题要考虑画图方便且符合要求.②由于位似中心选择的任意性,因此作已知图形的位似图形的结果是不唯一的.
【例1】如图,与位似,点为位似中心,位似比为,若的周长为6,则的周长是( )
A.16 B.9 C.6 D.4
【答案】D
【分析】根据位似变换的定义、相似三角形的性质计算即可.
【详解】解:和是位似图形,位似比为,
和的相似比为,
的周长的周长,
故选:D.
【点睛】此题主要考查了位似图形的性质,熟练掌握位似图形的性质是解题关键.
【例2】如图,与位似,点O为位似中心,若的周长等于周长的.,则的长度为( )
A.4 B.6 C.8 D.10
【答案】C
【分析】根据位似变换的概念得到,根据周长之比得到相似比,继而求解.
【详解】解:∵与位似,
∴,
∵的周长等于周长的,
∴相似比为,
∵,
∴,
故选C.
【点睛】本题考查的是位似变换、相似三角形的性质,掌握相似三角形的周长比等于相似比是解题的关键.
选择题
1.下列各组图形中的两个三角形均满足△ABC∽△DEF,这两个三角形不是位似图形的是 ( )
A B C D
2.如图,在外任取一点,连接、、,并分别取它们的中点、、,顺次连接、、得到,则下列说法错误的是( )
A.与是位似图形 B.与是相似图形
C.与的周长比是 D.与的面积比是
3.如图,在平面直角坐标系中,矩形ABCD的顶点坐标分别为A(-3,2),B(-3,-2),C(3,-2),D(3,2),以原点为位似中心,在矩形ABCD的内部画矩形EFGH,使矩形EFGH是矩形ABCD的位似图形,且相似比为2∶1,则矩形EFGH的周长为 ( )
A.20 B.15 C.10 D.
4.如图,已知与是以点为位似中心的位似图形,若,,,则点A的坐标为( )
A. B. C. D.
5.如图,在正方形网格中,以点为位似中心,的位似图形可以是( )
A. B. C. D.
6.如图,在△ABC外任取一点O,连接AO、BO、CO,并分别取它们的中点D、E、F,顺次连接DE、EF、DF得到△DEF,则下列说法错误的是 ( )
A.△DEF与△ABC是位似图形
B.△DEF与△ABC是相似图形
C.△DEF与△ABC的周长比是1∶2
D.△DEF与△ABC的面积比是1∶2
7.如图,与是位似图形,则位似中心为( )
A.点 B.点 C.点 D.点
8.如图,在平面直角坐标系中,每个小正方形的边长均为1个单位长度,△ABO的顶点坐标分别为A(-2,-1),B(-2,-3),O(0,0),△A1B1O1的顶点坐标分别为A1(1,-1),B1(1,-5),O1(5,1),△ABO与△A1B1O1是以点P为位似中心的位似图形,则P点的坐标为 .
9.如图,在平面直角坐标系中,与是位似图形,且顶点都在格点上,则位似中心的坐标是( )
A. B. C. D.
10.如图,在直角坐标系中,与是位似图形,已知点,则位似中心的坐标是( )
A. B. C. D.
填空题
11.如图,在平面直角坐标系中,阴影所示的两个正方形是位似图形,若位似中心在两个正方形之间,则位似中心的坐标为 .
12.如图,△A'B'C'与△ABC是位似图形,点O为位似中心,若OA'=AA',则△A'B'C'与△ABC的面积比为 .
13.如图,与位似,点为位似中心,若,的周长为4,则的周长为 .
14.由12个有公共顶点O的直角三角形拼成如图所示的图形,.若,则图中与位似的三角形中,边对应边的长为 .
15.如图,在平面直角坐标系中,点、的坐标分别为、,点、的坐标分别为、.若线段和是位似图形,且位似中心在轴上,则位似中心的坐标为 .
三、解答题
16.如图,已知图中的每个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点,若与是位似图形且顶点均在格点上.
(1)在图中画出位似中心的位置,并写出位似中心的坐标;
(2)与的位似比为__________,面积比为__________.
17.如图,在平面直角坐标系中,△ABC和△A1B1C1关于点E成中心对称,
(1)在图中标出点E,且点E的坐标为 ;
(2)点P(a,b)是△ABC边AB上一点,△ABC经过平移后点P的对应点P'的坐标为(a-6,b+2),请画出上述平移后的△A2B2C2,此时A2的坐标为 ,C2的坐标为 ;
(3)若△A1B1C1和△A2B2C2关于点F成位似三角形,则点F的坐标为 .
18.如图,图中的小方格都是边长为的正方形,与是关于点为位似中心的位似图形,它们的顶点都在小正方形的顶点上.
(1)画出位似中心点;
(2)求出与的位似比;
(3)以点为位似中心,再画一个,使它与的位似比等于.
(一)课后反思:
本节课我学会了:
本节课存在的问题:
把本节课所学知识画出思维导图
参考答案
【答案】 B
【分析】根据位似图形的概念,A、C、D三个图形中的两个三角形都是位似图形,B中的两个三角形不符合位似图形的概念,故不是位似图形.故选B.
2.【答案】C
【分析】根据位似图形的性质得出与是位似图形,根据位似图形一定是相似图形得出与是相似图形,再根据周长比等于位似比以及根据面积比等于相似比的平方即可解答.
【详解】解:根据位似性质可得:
A、与是位似图形,故A选项正确,不符合题意;
B、与是相似图形,故B选项正确,不符合题意;
C、∵点D,E,F,为中点,
∴将的三边缩小到原来的得到,
∴与的周长之比为2:1,故C选项不正确,符合题意;
D、∵面积比等于相似比的平方,
∴与的面积之比为4:1,故D选项正确,不符合题意.
故选:C.
【点睛】本题主要考查了位似图形的性质,正确的记忆位似图形性质是解决问题的关键.
3.【答案】 C
【分析】∵矩形ABCD的顶点坐标分别为A(-3,2),B(-3,-2),C(3,-2),D(3,2),∴矩形ABCD的周长为4+6+4+6=20,∵矩形ABCD与矩形EFGH的相似比为2∶1,∴矩形ABCD与矩形EFGH的周长比为2∶1,∴矩形EFGH的周长为10.故选C.
4.【答案】B
【分析】根据位似变换的性质得到,相似比为,进而求出点A的坐标.
【详解】解:∵与是以点为位似中心的位似图形,,,
∴,相似比为,
∵,
点A的坐标为,
故选:B.
【点睛】本题考查的是位似变换的概念和性质,求出与的相似比为是解题的关键.
5.【答案】C
【分析】根据位似的性质,连接并延长,观察交点即可求解.
【详解】解:如图所示,连接并延长,
∴的位似图形是.
故选:C.
【点睛】本题考查了位似图形的性质,熟练掌握位似图形的性质是解题的关键.
【答案】 D
【分析】∵AO、BO、CO的中点分别为D、E、F,∴EF=BC,DF=AC,DE=AB,∴===,∴△DEF∽△ABC,∵△DEF与△ABC的对应点连线相交于点O,∴△DEF与△ABC是位似图形,位似中心为点O,∵△DEF与△ABC的相似比为1∶2,∴△DEF与△ABC的周长比是1∶2,△DEF与△ABC的面积比是1∶4,∴D选项说法错误.故选D.
7.【答案】D
【分析】根据位似中心是位似点连线的交点判断即可.
【详解】如图,根据位似中心是位似点连线的交点,可知点P为位似中心,
故选D.
【点睛】本题考查了三角形的位似,清楚位似中心是位似点连线的交点是解题的关键.
8.答案 (-5,-1)
解析 如图,P点的坐标为(-5,-1).
9.B
【分析】根据位似图形的定义,画出位似中心,即可得出结果.
【详解】解:∵与是位似图形,
连接并延长,交于点,则点即为位似中心,如图所示:
由图可知:;
故选B.
【点睛】本题考查坐标系下求位似中心的坐标.熟练掌握位似图形的定义,确定位似中心的位置,是解题的关键.
10.B
【分析】根据位似图形的对应顶点的连线交于一点并结合网格图中的格点特征确定位似中心.
【详解】连接,并延长,交于点,点即为位似中心,如图,
∴点坐标为,
故答案为:.
【点睛】此题考查了位似变换的概念、坐标与图形性质,掌握如果两个图形不仅是相似图形,而且对应顶点的连线相交于一点,对应边互相平行,那么这样的两个图形叫做位似图形,这个点叫做位似中心是解题的关键.
11.
【分析】连接各组对应点,它们在两个正方形之间相交于点,则点为位似中心,然后写出点坐标即可.
【详解】解:如图,点为位似中心,.
故答案为:.
【点睛】本题考查位似变换:位似的两个图形不仅是相似图形,而且对应顶点的连线相交于一点,对应边互相平行(或共线),掌握位似变换的性质是解题的关键.
12. 【答案】 1∶4
【解析】 ∵△A'B'C'与△ABC是位似图形,点O为位似中心,且OA'=AA',∴S△A'B'C'∶S△ABC=(OA'∶OA)2=(1∶2)2=1∶4.
13.2
【分析】根据与位似,得出,推出,进而得出,根据相似三角形周长比等于相似比,即可求解.
【详解】解:∵与位似,
∴,
∵,
∴,
∴,
∴,
∵的周长为4,
∴的周长为2,
故答案为:2.
【点睛】本题主要考查了相似三角形那个的判定和性质,位似三角形的性质,解题的关键是掌握相似三角形周长比等于相似比.
14./
【分析】根据勾股定理和直角三角形中30度角所对的直角边等于斜边的一半,求出,,找出规律得出,即可得出答案.
【详解】解:∵在中,,,
∴,
根据勾股定理得:,
即,
解得:,
同理可得:,
…
,
∵与位似,与是对应边,
∴边对应边的长为.
故答案为:.
【点睛】本题主要考查了勾股定理,直角三角形的性质,图形规律探索,位似图形的定义,解题的关键是熟练掌握勾股定理和直角三角形中30度角所对的直角边等于斜边的一半.
15.
【分析】根据题意,位似中心在轴上,如图所示,连接与轴交于点,则点是位似中心,运用待定系数法求出直线的解析式,令,即可求解.
【详解】解:如图所示,连接与轴交于点,则点是位似中心,
∵,,
∴设所在直线的解析式为,
∴,解得,,
∴直线的解析式为,
当时,,
∴位似中心的坐标是,
故答案为:.
【点睛】本题主要考查位似与一次函数的综合,掌握位似的定义,待定系数法求一次函数解析式是解题的关键.
16.(1)见解析
(2),
【分析】(1)连接、,两线相交于点D,根据位似中心的概念、结合图形解答即可;
(2)根据,,即可得出相似比和面积比.
【详解】(1)解:如图,位似中心的坐标为:.
(2)解:∵,,
∴与的位似比为:,
与的面积比为:.
故答案为:,.
【点睛】本题考查的是位似变换的概念和性质,如果两个图形不仅是相似图形,而且对应顶点的连线所在直线相交于一点,对应边互相平行,那么这样的两个图形叫做位似图形,这个点叫做位似中心.
17.【解析】 (1)如图,连接BB1,线段BB1的中点即为点E.
∵B(1,1),B1(-1,-3),
∴E(0,-1).
(2)∵点P(a,b)是△ABC边AB上一点,△ABC经过平移后点P的对应点P'的坐标为(a-6,b+2),
∴△ABC向左平移了6个单位,向上平移了2个单位,∴△A2B2C2如图所示.
∵A(3,2),C(4,0),
∴A2(-3,4),C2(-2,2).
(3)∵连接A1A2与B1B2,它们交于点(-3,0),
∴F(-3,0).
18.(1)见解析
(2)
(3)见解析
【分析】(1)连接,分别延长三条线段交于一点O,则点O即为所求;
(2)与的位似比等于与的比,也等于与在水平线上的投影比,即,即可得到答案;
(3)按照位似图形的作图方法作即可.
【详解】(1)解:如图,点即为所求.
(2)与的位似比等于与的比,也等于与在水平线上的投影比,即.
∴与的位似比为.
(3)如图,为所求.
【点睛】此题考查了位似图形和位似图形的作图,熟练掌握位似图形的作图和性质是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
