九年级数学上册 23.2 解直角三角形及其应用 导学案(知识清单 典型例题 巩固提升)
文档属性
| 名称 | 九年级数学上册 23.2 解直角三角形及其应用 导学案(知识清单 典型例题 巩固提升) |

|
|
| 格式 | docx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-08 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
23.2 解直角三角形及其应用 导学案
(一)学习目标:
1.理解解直角三角形的含义,会运用勾股定理、直角三角形的两个锐角互余及锐角三角函数解直角三角形;
2.能通过作高线构造直角三角形解非直角三角形;
3.会用解直角三角形中的有关知识建立数学模型,解决某些简单的实际问题.
(二)学习重难点:
重点:会运用勾股定理、直角三角形的两个锐角互余及锐角三角函数解直角三角形
难点:会利用解直角三角形,解决简单的实际问题。
阅读课本,识记知识:
知识点一 解直角三角形
1.解直角三角形的概念
一般地,直角三角形中,除直角外,共有五个元素,即三条边和两个锐角.由直角三角形中的已知元素,求出其余未知元素的过程,叫做解直角三角形.
在直角三角形中,除直角外的五个元素中,已知其中的两个元素(至少有一个是边),可求出其余的三个未知元素(知二求三)
一个直角三角形可解,则其面积和周长可求.但在一个解直角三角形的题中,如无特别说明,则不包括求面积和周长
2.直角三角形中五个元素(除直角外的)之间的关系
如图,在Rt△ABC中,已知∠C=90°,
三边之间的关系:.(勾股定理)
∠A+∠B=90°
边角之间的关系: ;;;
;;;.
3.解直角三角形的类型和解法
条件 解法步骤 图示
两 边 ①两直角边 由,求; ;
②斜边,一直角边(如) 由,求; ;
一 边 一 角 一直角边 和一锐角 ③锐角,邻边 如() ;
④锐角,对边 如() ;
⑤斜边,锐角 如() ;
知识点二 解直角三角形在实际问题中的应用
利用解直角三角形的知识解决实际问题的一般步骤
(1)将实际问题抽象为数学问题;
(2)根据问题中的条件选用合适的锐角三角函数解直角三角形;
(3)得到数学问题的答案;
(4)得到实际问题的答案.
2.实际问题中,常见的基本图形及相应的关系式
图形 关系式 图形 关系式
3.解直角三角形的常见类型
仰角和俯角
在测量中,我们把在视线与水平线所成的角中,视线在水平线上方的叫做仰角.
视线在水平线下方的叫俯角.
如图所示,PQ 为水平线,视线为PA时,则∠APQ为仰角;视线为PB时,则∠BPQ为俯角.
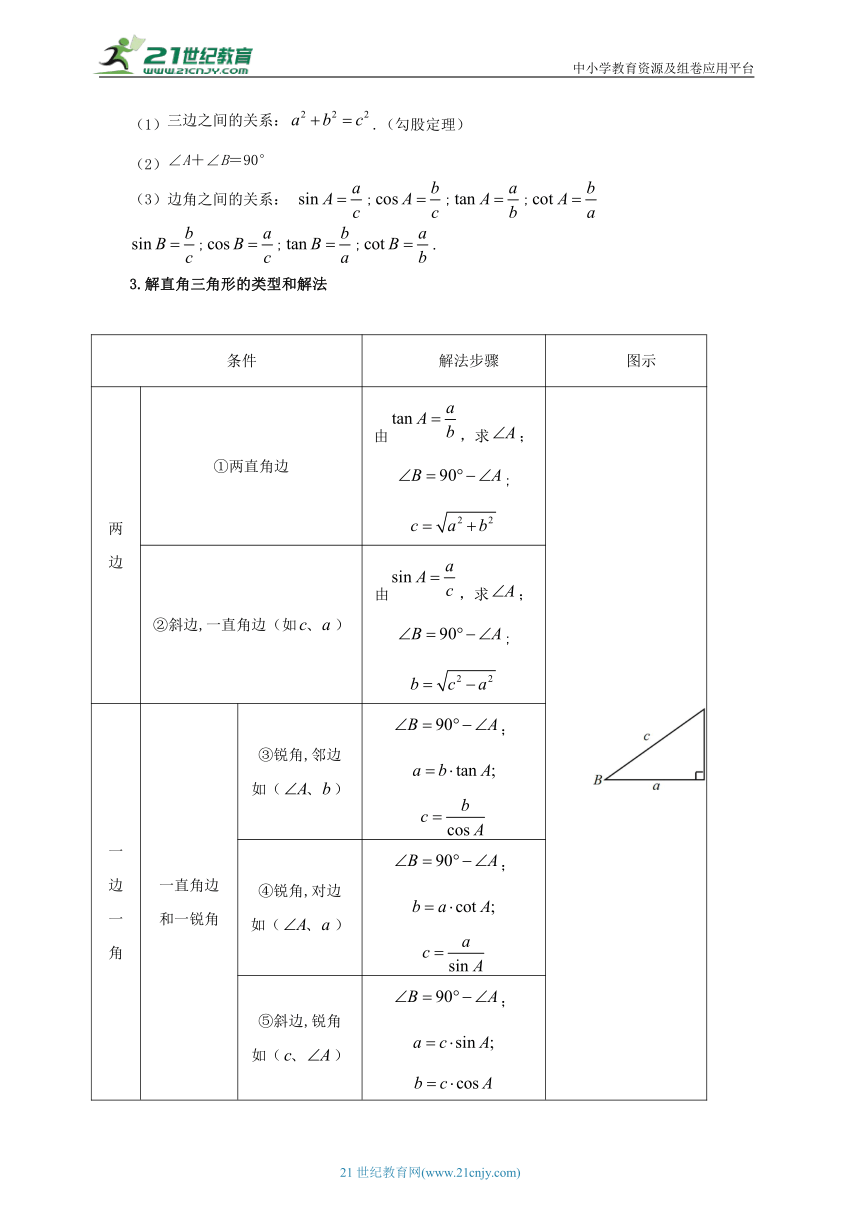
知识点三 方向角
指北或指南方向线与目标方向线所成的小于90°的角,叫方向角.
如图所示,目标方向线OA,OB,OC形成的方向角分别可以表示为北偏东30°、南偏东45°、北偏西30°,其中南偏东45°习惯上又叫做东南方向,北偏东 45°习惯上又叫做东北方向,北偏西45°习惯上又叫做西北方向,南偏西45习惯上又叫做西南方向.
知识点四 坡度与坡角
(1)坡角:坡面与水平面所成的夹角.如图中的
(2)坡度:我们通常把坡面的铅直高度和水平宽度的比叫做坡度.坡度也可写成的形式,在实际应用中常表示成的形式
(3)坡度与坡角的关系:.坡度是坡角的正切值,坡角越大,坡度也就越大
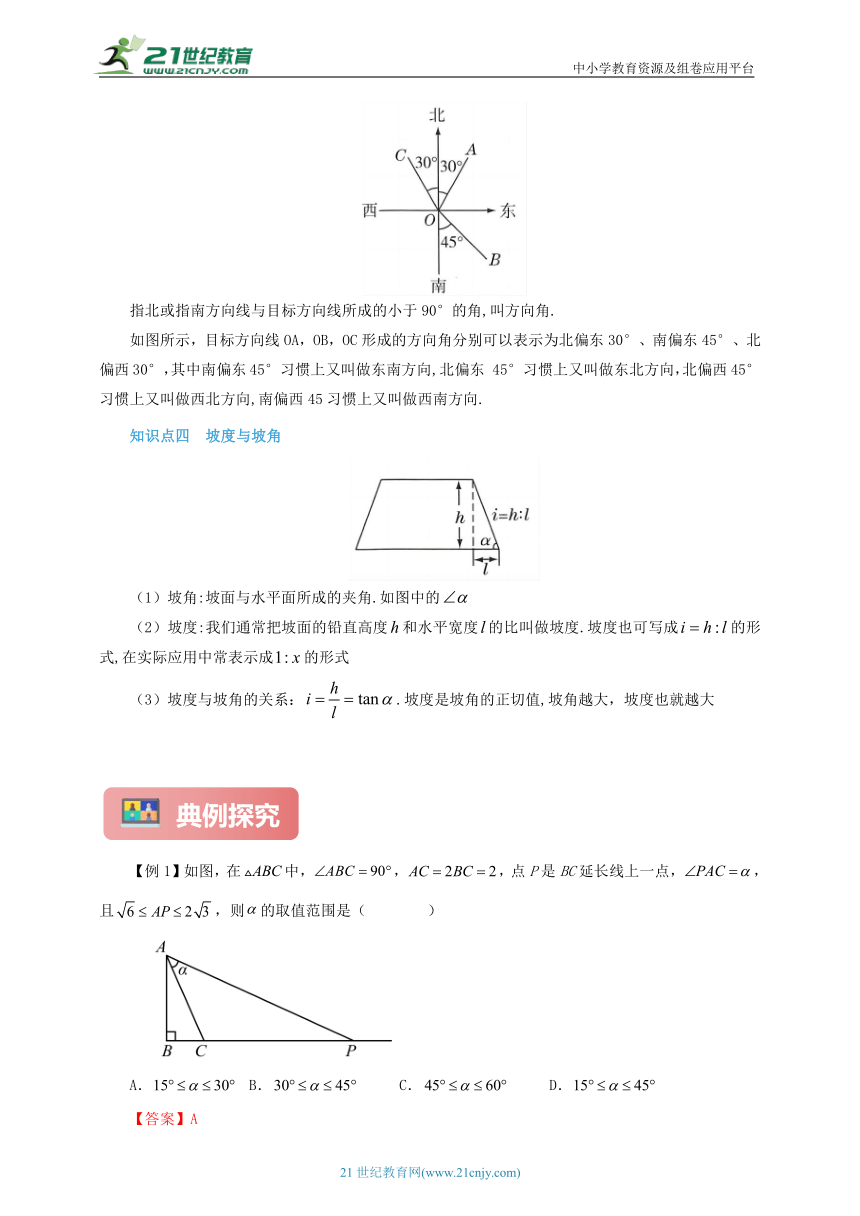
【例1】如图,在中,,,点P是BC延长线上一点,,且,则的取值范围是( )
A. B. C. D.
【答案】A
【分析】根据,,求出,则,求出,分别求出当时,当时的的度数,即可求出的取值范围.
【详解】解:∵,,
∴,
∴,
∴,
当时,
∴,
∴,则;
当时,
∴,
∴,则;
∵,
∴,
故选:A.
【点睛】本题主要考查了解直角三角形,解题的关键是掌握解直角三角形的方法和步骤,以及各个特殊角度的锐角三角函数值.
【例2】 如图,从航拍无人机看一栋楼顶部的仰角为,看这栋楼底部的俯角为,无人机与楼的水平距离为,则这栋楼的高度为( )
A. B. C. D.
【答案】B
【分析】过点作,垂足为,根据题意可得,然后分别在和中,利用锐角三角函数的定义求出的长,最后利用线段的和差关系进行计算即可解答.
【详解】解:过点作,垂足为,
根据题意可得,
在中,,
,
在中,,
,
.
故则这栋楼的高度为.
故选:B.
【点睛】本题考查了解直角三角形的应用,锐角三角函数的定义,根据题目的已知条件作出正确的辅助线是解题的关键.
选择题
1.如图,在中,,,,则的长为( )
A. B. C.4 D.5
2.如图,在四边形中,,,,,则四边形的面积为( )
A.48 B.50 C.52 D.54
3.如图,以的顶点O为坐标原点,所在直线为x轴,建立平面直角坐标系,若,,,,则点A的坐标是( )
A.(,) B.(,)
C.(,) D.(,)
4.如图,四边形ABCD的对角线AC、BD相交于O,∠AOD=60°,AC=BD=2,则这个四边形的面积是( )
A. B. C. D.
5.如图,,,底边BC上的高为,底边QR上的高为,则有( )
A. B. C. D.以上都有可能
6.如图,某农林部门用钢管为树木加固,已知钢管为4米,钢管与地面所成角,则固定点离地面的高度为( )米
A. B. C. D.
7.如图,小诚在距离旗杆底部B点的A处测得旗杆顶部C的仰角为,则旗杆BC的高为( )
A. B. C. D.
8.如图,在铁路建设中,需要确定隧道两洞口A和B的距离.点D,点E分别位于测绘点C的正北和正西方向.已知测得两定位点E和D与隧道口A和B的距离分别为和,测绘点H,G分别为,的中点,测绘方在测绘点H测得点G在点H的南偏西的方向上,且,则隧道的长约为( )(参考数据:)
A.1600m B.1300m C.980m D.900m
9.某区域平面示意图如图,点O在河的一侧,和表示两条互相垂直的公路.甲侦测员在处测得点位于北偏东,乙勘测员在处测得点位于南偏西,测得,,请求出点到的距离( ).(参考数据,,)
A.140 B.340 C.360 D.480
10.某兴趣小组开展了“笔记本电脑的张角大小、顶部边缘离桌面的高度与用眼舒适度关系”的实践探究活动,如图,当张角时,顶部边缘A处离桌面的高度AC的长为,此时用眼舒适度不太理想,小组成员调整张角大小继续探究,最后发现当张角(点是点的对应点),用眼舒适度较为理想,则此时顶部边缘处离地面的高度为( )
A. B. C. D.
填空题
11.如图,在中,,,是的中点,是的中点,,则线段的长为 .
12.如图,是边长为的等边三角形,点为高上的动点.连接,将绕点顺时针旋转得到.连接,,,则周长的最小值是 .
13.如图,在矩形中,,连接,点在上,平分 .
14.如图,热气球的探测器显示,从热气球看一栋楼顶部的仰角为,看这栋楼底部的俯角为,热气球与楼的水平距离,则这栋楼的高度约为 m(,,结果保留整数).
15.如图,小明在滨海大道的A处测得鸟岛P在北偏东的方向,他向正东方向前行200米到达B处,这时测得鸟岛P在他的北偏东方向,则岛P到滨海大道的A处的距离为 米(精确到1米).
三、解答题
16.如图,中,,点D为边上一点.
(1)求作四边形,使得四边形是菱形(尺规作图,保留作图痕迹);
(2)与的交点为O,连结,若, ,求的长.
17.如图,是的内接三角形,是的直径,,,点在上,连接并延长,交于点,连接,作,垂足为.
(1)求证:;
(2)若,求的长.
18.研学旅行继承和发展了我国传统游学“读万卷书,行万里路”的教育理念和人文精神,成为核心素养教育下的新内容和新方式.某中学组织学生进行研学活动,学生到达基地后,他们先从如图所示的基地门口A处沿南偏西方向走了400米,到达昆虫博览馆B处,再从B处向正东方向走了400米到达农耕体验区D处,然后从D处沿正北方向到达户外拓展区C处,最后再从C处沿北偏西方向回到A处.求户外拓展区C处与基地门口A处之间的距离.(参考数据:)
(一)课后反思:
本节课我学会了:
本节课存在的问题:
把本节课所学知识画出思维导图
参考答案
1.D
【分析】作于,根据,,算出和,再根据,算出,最后根据计算即可.
【详解】如下图,作于,
在中,,,
,,
在中,,
,
,
,
故选:D.
【点睛】本题考查了用锐角三角函数解非直角三角形,作垂直构造直角三角形是解题的关键.
2.A
【分析】连接AC,利用勾股定理求出AC,再根据进行计算即可求出结果.
【详解】解:连接,如图所示
,,
,
四边形的面积为48
故选:A.
【点睛】本题主要考查了四边形面积,解直角三角形的应用,勾股定理等知识,解题的关键是学会巧妙添加辅助线,构造直角三角形解决问题.
3.B
【分析】过点A作轴,垂足为B,根据正弦和余弦的定义,求出,,从而得到坐标.
【详解】解:如图,过点A作轴,垂足为B,
∴,,
∴,,
∴点A的坐标是(,),
故选B.
【点睛】本题考查了坐标与图形,解直角三角形,解题的关键是根据三角函数的定义求出,的长.
4.C
【分析】过B、D两点分别作AC的垂线,利用∠AOD=60°,可推出DG=DO,BH=BO,再利用四边形ABCD的面积等于△ACD的面积加上△ABC的面积,即可求出;
【详解】如图,过点D作DG⊥AC于点G,过点B作BH⊥AC于点H,
∵∠AOD=60°,
∴∠AOD=∠BOC=60°,
∴DG=DO,
同理可得:BH=BO,
S四边形ABCD=×AC×DG+×AC×BH
=×AC××(DO+BO)
=,
故选:C.
【点睛】本题考查含30°的直角三角形的性质和四边形面积的计算,熟练掌握含30°直角三角形的性质和不规则四边形面积的计算是解决本题的关键.
5.B
【分析】由已知可知高所对的斜边都为5,由正弦的定义可得到高关于正弦的表达式,比较正弦值即可得到答案.
【详解】解:如图,分别作出两三角形的高
∵
∴
∵
∴
∵
∴
故选:B.
【点睛】本题考查解直角三角形,依题意作高构造直角三角形是解题的关键.
6.D
【分析】根据题意可得:, 然后在 中, 利用锐角三角函数的定义,进行计算即可解答;
【详解】由题意得:
在中, 米,
∴ (米),
故选:D
【点睛】本题考查了解直角三角形的应用,熟练掌握锐角三角函数的定义是解题的关键
7.B
【分析】利用的正切求解即可.
【详解】解:由题意得,,,
∵,
∴.
故选B.
【点睛】本题考查了解直角三角形的应用,解决此问题的关键在于正确理解题意的基础上建立数学模型,把实际问题转化为数学问题.
8.B
【分析】先解直角三角形求出,然后根据三角形中位线定理求出,即可求解.
【详解】解:由题意知:,,,,
在中,,
∴,
∵点H,G分别为,的中点,
∴,
∴.
故选:B.
【点睛】本题考查解直角三角形的应用—方位角问题,三角形中位线定理等,明确题意,熟悉相关性质是解题的关键.
9.D
【分析】作于,于,设,根据矩形的性质用表示出、,根据正切的定义用表示出,根据题意列式计算即可.
【详解】解:作于,于,
则四边形为矩形,
,,
设,则,,
在中,,
,则,
在中,,
由题意得,,
解得,,
即点到的距离约为480,
故选:D.
【点睛】本题考查的是解直角三角形的应用,掌握锐角三角函数的定义、正确标注方向角是解题的关键.
10.B
【分析】根据,得到,再根据,得到,在中根据三角函数即可求解.
【详解】解:∵,
∴,
在中,,
∴,
由题意得:,
∵,
∴,
在中,
∴此时顶部边缘处离桌面的高度的长约为,
故选:B.
【点睛】本题主要考查了解直角三角形的应用,熟练掌握三角函数的定义是解题的关键.
11.
【分析】根据含角的直角三角形的性质可知,进一步可知,根据等腰三角形的性质可知,,根据,求出的长,再根据,即可求出的长.
【详解】解:,,
,,
是的中点,
,
,
是的中点,
平分,,
,,
,,
,
,
,
故答案为:.
【点睛】本题考查了含角的直角三角形的性质,等腰三角形的性质,特殊角的三角函数,熟练掌握这些知识是解题的关键.
12.
【分析】根据等边三角形的性质可得,,推得,根据全等三角形的判定和性质可得,,过点作,交的延长线于点,延长到,使得,连接,,与交于点,连接,,根据三角形内角和定理可得,根据含角的直角三角形的性质可得,根据等边三角形的判定可得为等边三角形,根据特殊角的锐角三角函数可求得,根据垂直平分线的性质可得,,求得,当与重合时,即、、三点共线时,的值最小,即可求解.
【详解】解:∵是等边三角形,
∴,,
∵,
∴,
∵,,,
∴,
∴,
∵是等边三角形,是高,
∴,,
过点作,交的延长线于点,延长到,使得,连接,,与交于点,连接,,如图:
则,
在中,,
∴,,
故,
∴,
∴为等边三角形,
在中,,
∵,,
即垂直平分,
∴,,
∴,
,
∴当与重合时,即、、三点共线时,的值最小为:,
∴的周长的最小值为.
故答案为:.
【点睛】本题主要考查了等边三角形的判定和性质,旋转的性质,全等三角形的判定和性质,解直角三角形,含角的直角三角形的性质,解题的关键在于证明三角形全等,确定点运动轨迹.
13./
【分析】过点D作,由平分可得是等腰直角三角形,再根据矩形性质和勾股定理易求对角线长,进而解三角形求出、即可解答.
【详解】解:过点D作,如图:
∵平分,
∴,
∴,
∵在矩形中,,
∴,,,
∴,
∴,,
∴,
,
∴,
故答案为:.
【点睛】本题主要考查了矩形性质和解三角形,解题关键是过点D作构造是等腰直角三角形,再解三角形.
14.273
【分析】根据题意可得:,然后分别在和中,利用锐角三角函数的定义求出和的长,从而利用线段的和差关系进行计算,即可解答.
【详解】解:由题意得:,
在中,,,
,
在中,,
,
,
这栋楼的高度约为,
故答案为:273.
【点睛】本题考查了解直角三角形的应用﹣仰角俯角问题,熟练掌握锐角三角函数的定义是解题的关键.
15.
【分析】在图中两个直角三角形中,先根据已知角的正切函数,分别求出,根据它们之间的关系,构建方程求出,再利用直角三角形30度角的性质求解即可.
【详解】过点P作于点D
由已知得,在中,,
在中,,
解得,,
∴(米),
∴(米),
答:岛P到滨海大道的A处的距离为米.
故答案为.
【点睛】此题考查的是解直角三角形的应用,关键明确解一般三角形的问题可以转化为解直角三角形的问题,解决的方法就是作高线.
16(1)见解析;
(2).
【分析】(1)如图所示,①作线段的垂直平分线,交于点D;②以点B为圆心,以为半径画弧,交垂直平分线于点E;即得所求.
(2)过点E作于点F,由菱形得,,,可证四边形是矩形,解得,,由勾股定理,由斜边中线定理,得.
【详解】(1)解:如图所示,①作线段的垂直平分线,交于点D;
②以点B为圆心,以为半径画弧,交垂直平分线于点E;
③连接,,,即得所求.
(2)过点E作于点F,
∵四边形是菱形,
∴,,
∵,
∴四边形是矩形,
∴,
在中,∵,
∴,
∴,
∴,
∴,
∴,
∵,O是的中点,
∴,
∴的长为.
【点睛】本题考查尺规作图,菱形的性质,矩形的判定和性质,解直角三角形;构造直角三角形求解线段是解题的关键.
17.(1)见解析
(2)
【分析】(1)根据圆周角定理得,进而可以证明结论;
(2)过点作,垂足为,证明,得,代入值即可解决问题.
【详解】(1)解:证明:为直径,
,
,
,
所对的圆周角为和,
,
;
(2)如图,过点作,垂足为,
,,,
,
,
,
,
,
AC=FC
,
,
,
,
,
.
【点睛】本题考查圆周角定理、相似三角形的判定与性质、解直角三角形、勾股定理等知识点,解决本题的关键是得到.
18.250米
【分析】过点A作于点E,过点C作于点F,解直角三角形,求出的长,进而求出的长,再解直角三角形,求出的长即可.
【详解】解∶如图,过点A作于点E,过点C作于点F,则四边形是矩形,
∴,
根据题意可知∶米,米,,
∴(米),,
∴(米),
∴米.
在中,,
∴(米).
答:户外拓展区C处与基地门口A处之间的距离为250米.
【点睛】本题考查解直角三角形的应用.解题的关键是添加辅助线,构造直角三角形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
23.2 解直角三角形及其应用 导学案
(一)学习目标:
1.理解解直角三角形的含义,会运用勾股定理、直角三角形的两个锐角互余及锐角三角函数解直角三角形;
2.能通过作高线构造直角三角形解非直角三角形;
3.会用解直角三角形中的有关知识建立数学模型,解决某些简单的实际问题.
(二)学习重难点:
重点:会运用勾股定理、直角三角形的两个锐角互余及锐角三角函数解直角三角形
难点:会利用解直角三角形,解决简单的实际问题。
阅读课本,识记知识:
知识点一 解直角三角形
1.解直角三角形的概念
一般地,直角三角形中,除直角外,共有五个元素,即三条边和两个锐角.由直角三角形中的已知元素,求出其余未知元素的过程,叫做解直角三角形.
在直角三角形中,除直角外的五个元素中,已知其中的两个元素(至少有一个是边),可求出其余的三个未知元素(知二求三)
一个直角三角形可解,则其面积和周长可求.但在一个解直角三角形的题中,如无特别说明,则不包括求面积和周长
2.直角三角形中五个元素(除直角外的)之间的关系
如图,在Rt△ABC中,已知∠C=90°,
三边之间的关系:.(勾股定理)
∠A+∠B=90°
边角之间的关系: ;;;
;;;.
3.解直角三角形的类型和解法
条件 解法步骤 图示
两 边 ①两直角边 由,求; ;
②斜边,一直角边(如) 由,求; ;
一 边 一 角 一直角边 和一锐角 ③锐角,邻边 如() ;
④锐角,对边 如() ;
⑤斜边,锐角 如() ;
知识点二 解直角三角形在实际问题中的应用
利用解直角三角形的知识解决实际问题的一般步骤
(1)将实际问题抽象为数学问题;
(2)根据问题中的条件选用合适的锐角三角函数解直角三角形;
(3)得到数学问题的答案;
(4)得到实际问题的答案.
2.实际问题中,常见的基本图形及相应的关系式
图形 关系式 图形 关系式
3.解直角三角形的常见类型
仰角和俯角
在测量中,我们把在视线与水平线所成的角中,视线在水平线上方的叫做仰角.
视线在水平线下方的叫俯角.
如图所示,PQ 为水平线,视线为PA时,则∠APQ为仰角;视线为PB时,则∠BPQ为俯角.
知识点三 方向角
指北或指南方向线与目标方向线所成的小于90°的角,叫方向角.
如图所示,目标方向线OA,OB,OC形成的方向角分别可以表示为北偏东30°、南偏东45°、北偏西30°,其中南偏东45°习惯上又叫做东南方向,北偏东 45°习惯上又叫做东北方向,北偏西45°习惯上又叫做西北方向,南偏西45习惯上又叫做西南方向.
知识点四 坡度与坡角
(1)坡角:坡面与水平面所成的夹角.如图中的
(2)坡度:我们通常把坡面的铅直高度和水平宽度的比叫做坡度.坡度也可写成的形式,在实际应用中常表示成的形式
(3)坡度与坡角的关系:.坡度是坡角的正切值,坡角越大,坡度也就越大
【例1】如图,在中,,,点P是BC延长线上一点,,且,则的取值范围是( )
A. B. C. D.
【答案】A
【分析】根据,,求出,则,求出,分别求出当时,当时的的度数,即可求出的取值范围.
【详解】解:∵,,
∴,
∴,
∴,
当时,
∴,
∴,则;
当时,
∴,
∴,则;
∵,
∴,
故选:A.
【点睛】本题主要考查了解直角三角形,解题的关键是掌握解直角三角形的方法和步骤,以及各个特殊角度的锐角三角函数值.
【例2】 如图,从航拍无人机看一栋楼顶部的仰角为,看这栋楼底部的俯角为,无人机与楼的水平距离为,则这栋楼的高度为( )
A. B. C. D.
【答案】B
【分析】过点作,垂足为,根据题意可得,然后分别在和中,利用锐角三角函数的定义求出的长,最后利用线段的和差关系进行计算即可解答.
【详解】解:过点作,垂足为,
根据题意可得,
在中,,
,
在中,,
,
.
故则这栋楼的高度为.
故选:B.
【点睛】本题考查了解直角三角形的应用,锐角三角函数的定义,根据题目的已知条件作出正确的辅助线是解题的关键.
选择题
1.如图,在中,,,,则的长为( )
A. B. C.4 D.5
2.如图,在四边形中,,,,,则四边形的面积为( )
A.48 B.50 C.52 D.54
3.如图,以的顶点O为坐标原点,所在直线为x轴,建立平面直角坐标系,若,,,,则点A的坐标是( )
A.(,) B.(,)
C.(,) D.(,)
4.如图,四边形ABCD的对角线AC、BD相交于O,∠AOD=60°,AC=BD=2,则这个四边形的面积是( )
A. B. C. D.
5.如图,,,底边BC上的高为,底边QR上的高为,则有( )
A. B. C. D.以上都有可能
6.如图,某农林部门用钢管为树木加固,已知钢管为4米,钢管与地面所成角,则固定点离地面的高度为( )米
A. B. C. D.
7.如图,小诚在距离旗杆底部B点的A处测得旗杆顶部C的仰角为,则旗杆BC的高为( )
A. B. C. D.
8.如图,在铁路建设中,需要确定隧道两洞口A和B的距离.点D,点E分别位于测绘点C的正北和正西方向.已知测得两定位点E和D与隧道口A和B的距离分别为和,测绘点H,G分别为,的中点,测绘方在测绘点H测得点G在点H的南偏西的方向上,且,则隧道的长约为( )(参考数据:)
A.1600m B.1300m C.980m D.900m
9.某区域平面示意图如图,点O在河的一侧,和表示两条互相垂直的公路.甲侦测员在处测得点位于北偏东,乙勘测员在处测得点位于南偏西,测得,,请求出点到的距离( ).(参考数据,,)
A.140 B.340 C.360 D.480
10.某兴趣小组开展了“笔记本电脑的张角大小、顶部边缘离桌面的高度与用眼舒适度关系”的实践探究活动,如图,当张角时,顶部边缘A处离桌面的高度AC的长为,此时用眼舒适度不太理想,小组成员调整张角大小继续探究,最后发现当张角(点是点的对应点),用眼舒适度较为理想,则此时顶部边缘处离地面的高度为( )
A. B. C. D.
填空题
11.如图,在中,,,是的中点,是的中点,,则线段的长为 .
12.如图,是边长为的等边三角形,点为高上的动点.连接,将绕点顺时针旋转得到.连接,,,则周长的最小值是 .
13.如图,在矩形中,,连接,点在上,平分 .
14.如图,热气球的探测器显示,从热气球看一栋楼顶部的仰角为,看这栋楼底部的俯角为,热气球与楼的水平距离,则这栋楼的高度约为 m(,,结果保留整数).
15.如图,小明在滨海大道的A处测得鸟岛P在北偏东的方向,他向正东方向前行200米到达B处,这时测得鸟岛P在他的北偏东方向,则岛P到滨海大道的A处的距离为 米(精确到1米).
三、解答题
16.如图,中,,点D为边上一点.
(1)求作四边形,使得四边形是菱形(尺规作图,保留作图痕迹);
(2)与的交点为O,连结,若, ,求的长.
17.如图,是的内接三角形,是的直径,,,点在上,连接并延长,交于点,连接,作,垂足为.
(1)求证:;
(2)若,求的长.
18.研学旅行继承和发展了我国传统游学“读万卷书,行万里路”的教育理念和人文精神,成为核心素养教育下的新内容和新方式.某中学组织学生进行研学活动,学生到达基地后,他们先从如图所示的基地门口A处沿南偏西方向走了400米,到达昆虫博览馆B处,再从B处向正东方向走了400米到达农耕体验区D处,然后从D处沿正北方向到达户外拓展区C处,最后再从C处沿北偏西方向回到A处.求户外拓展区C处与基地门口A处之间的距离.(参考数据:)
(一)课后反思:
本节课我学会了:
本节课存在的问题:
把本节课所学知识画出思维导图
参考答案
1.D
【分析】作于,根据,,算出和,再根据,算出,最后根据计算即可.
【详解】如下图,作于,
在中,,,
,,
在中,,
,
,
,
故选:D.
【点睛】本题考查了用锐角三角函数解非直角三角形,作垂直构造直角三角形是解题的关键.
2.A
【分析】连接AC,利用勾股定理求出AC,再根据进行计算即可求出结果.
【详解】解:连接,如图所示
,,
,
四边形的面积为48
故选:A.
【点睛】本题主要考查了四边形面积,解直角三角形的应用,勾股定理等知识,解题的关键是学会巧妙添加辅助线,构造直角三角形解决问题.
3.B
【分析】过点A作轴,垂足为B,根据正弦和余弦的定义,求出,,从而得到坐标.
【详解】解:如图,过点A作轴,垂足为B,
∴,,
∴,,
∴点A的坐标是(,),
故选B.
【点睛】本题考查了坐标与图形,解直角三角形,解题的关键是根据三角函数的定义求出,的长.
4.C
【分析】过B、D两点分别作AC的垂线,利用∠AOD=60°,可推出DG=DO,BH=BO,再利用四边形ABCD的面积等于△ACD的面积加上△ABC的面积,即可求出;
【详解】如图,过点D作DG⊥AC于点G,过点B作BH⊥AC于点H,
∵∠AOD=60°,
∴∠AOD=∠BOC=60°,
∴DG=DO,
同理可得:BH=BO,
S四边形ABCD=×AC×DG+×AC×BH
=×AC××(DO+BO)
=,
故选:C.
【点睛】本题考查含30°的直角三角形的性质和四边形面积的计算,熟练掌握含30°直角三角形的性质和不规则四边形面积的计算是解决本题的关键.
5.B
【分析】由已知可知高所对的斜边都为5,由正弦的定义可得到高关于正弦的表达式,比较正弦值即可得到答案.
【详解】解:如图,分别作出两三角形的高
∵
∴
∵
∴
∵
∴
故选:B.
【点睛】本题考查解直角三角形,依题意作高构造直角三角形是解题的关键.
6.D
【分析】根据题意可得:, 然后在 中, 利用锐角三角函数的定义,进行计算即可解答;
【详解】由题意得:
在中, 米,
∴ (米),
故选:D
【点睛】本题考查了解直角三角形的应用,熟练掌握锐角三角函数的定义是解题的关键
7.B
【分析】利用的正切求解即可.
【详解】解:由题意得,,,
∵,
∴.
故选B.
【点睛】本题考查了解直角三角形的应用,解决此问题的关键在于正确理解题意的基础上建立数学模型,把实际问题转化为数学问题.
8.B
【分析】先解直角三角形求出,然后根据三角形中位线定理求出,即可求解.
【详解】解:由题意知:,,,,
在中,,
∴,
∵点H,G分别为,的中点,
∴,
∴.
故选:B.
【点睛】本题考查解直角三角形的应用—方位角问题,三角形中位线定理等,明确题意,熟悉相关性质是解题的关键.
9.D
【分析】作于,于,设,根据矩形的性质用表示出、,根据正切的定义用表示出,根据题意列式计算即可.
【详解】解:作于,于,
则四边形为矩形,
,,
设,则,,
在中,,
,则,
在中,,
由题意得,,
解得,,
即点到的距离约为480,
故选:D.
【点睛】本题考查的是解直角三角形的应用,掌握锐角三角函数的定义、正确标注方向角是解题的关键.
10.B
【分析】根据,得到,再根据,得到,在中根据三角函数即可求解.
【详解】解:∵,
∴,
在中,,
∴,
由题意得:,
∵,
∴,
在中,
∴此时顶部边缘处离桌面的高度的长约为,
故选:B.
【点睛】本题主要考查了解直角三角形的应用,熟练掌握三角函数的定义是解题的关键.
11.
【分析】根据含角的直角三角形的性质可知,进一步可知,根据等腰三角形的性质可知,,根据,求出的长,再根据,即可求出的长.
【详解】解:,,
,,
是的中点,
,
,
是的中点,
平分,,
,,
,,
,
,
,
故答案为:.
【点睛】本题考查了含角的直角三角形的性质,等腰三角形的性质,特殊角的三角函数,熟练掌握这些知识是解题的关键.
12.
【分析】根据等边三角形的性质可得,,推得,根据全等三角形的判定和性质可得,,过点作,交的延长线于点,延长到,使得,连接,,与交于点,连接,,根据三角形内角和定理可得,根据含角的直角三角形的性质可得,根据等边三角形的判定可得为等边三角形,根据特殊角的锐角三角函数可求得,根据垂直平分线的性质可得,,求得,当与重合时,即、、三点共线时,的值最小,即可求解.
【详解】解:∵是等边三角形,
∴,,
∵,
∴,
∵,,,
∴,
∴,
∵是等边三角形,是高,
∴,,
过点作,交的延长线于点,延长到,使得,连接,,与交于点,连接,,如图:
则,
在中,,
∴,,
故,
∴,
∴为等边三角形,
在中,,
∵,,
即垂直平分,
∴,,
∴,
,
∴当与重合时,即、、三点共线时,的值最小为:,
∴的周长的最小值为.
故答案为:.
【点睛】本题主要考查了等边三角形的判定和性质,旋转的性质,全等三角形的判定和性质,解直角三角形,含角的直角三角形的性质,解题的关键在于证明三角形全等,确定点运动轨迹.
13./
【分析】过点D作,由平分可得是等腰直角三角形,再根据矩形性质和勾股定理易求对角线长,进而解三角形求出、即可解答.
【详解】解:过点D作,如图:
∵平分,
∴,
∴,
∵在矩形中,,
∴,,,
∴,
∴,,
∴,
,
∴,
故答案为:.
【点睛】本题主要考查了矩形性质和解三角形,解题关键是过点D作构造是等腰直角三角形,再解三角形.
14.273
【分析】根据题意可得:,然后分别在和中,利用锐角三角函数的定义求出和的长,从而利用线段的和差关系进行计算,即可解答.
【详解】解:由题意得:,
在中,,,
,
在中,,
,
,
这栋楼的高度约为,
故答案为:273.
【点睛】本题考查了解直角三角形的应用﹣仰角俯角问题,熟练掌握锐角三角函数的定义是解题的关键.
15.
【分析】在图中两个直角三角形中,先根据已知角的正切函数,分别求出,根据它们之间的关系,构建方程求出,再利用直角三角形30度角的性质求解即可.
【详解】过点P作于点D
由已知得,在中,,
在中,,
解得,,
∴(米),
∴(米),
答:岛P到滨海大道的A处的距离为米.
故答案为.
【点睛】此题考查的是解直角三角形的应用,关键明确解一般三角形的问题可以转化为解直角三角形的问题,解决的方法就是作高线.
16(1)见解析;
(2).
【分析】(1)如图所示,①作线段的垂直平分线,交于点D;②以点B为圆心,以为半径画弧,交垂直平分线于点E;即得所求.
(2)过点E作于点F,由菱形得,,,可证四边形是矩形,解得,,由勾股定理,由斜边中线定理,得.
【详解】(1)解:如图所示,①作线段的垂直平分线,交于点D;
②以点B为圆心,以为半径画弧,交垂直平分线于点E;
③连接,,,即得所求.
(2)过点E作于点F,
∵四边形是菱形,
∴,,
∵,
∴四边形是矩形,
∴,
在中,∵,
∴,
∴,
∴,
∴,
∴,
∵,O是的中点,
∴,
∴的长为.
【点睛】本题考查尺规作图,菱形的性质,矩形的判定和性质,解直角三角形;构造直角三角形求解线段是解题的关键.
17.(1)见解析
(2)
【分析】(1)根据圆周角定理得,进而可以证明结论;
(2)过点作,垂足为,证明,得,代入值即可解决问题.
【详解】(1)解:证明:为直径,
,
,
,
所对的圆周角为和,
,
;
(2)如图,过点作,垂足为,
,,,
,
,
,
,
,
AC=FC
,
,
,
,
,
.
【点睛】本题考查圆周角定理、相似三角形的判定与性质、解直角三角形、勾股定理等知识点,解决本题的关键是得到.
18.250米
【分析】过点A作于点E,过点C作于点F,解直角三角形,求出的长,进而求出的长,再解直角三角形,求出的长即可.
【详解】解∶如图,过点A作于点E,过点C作于点F,则四边形是矩形,
∴,
根据题意可知∶米,米,,
∴(米),,
∴(米),
∴米.
在中,,
∴(米).
答:户外拓展区C处与基地门口A处之间的距离为250米.
【点睛】本题考查解直角三角形的应用.解题的关键是添加辅助线,构造直角三角形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
