第十一章三角形单元测试(含答案)2024-2025学年人教版数学八年级上册
文档属性
| 名称 | 第十一章三角形单元测试(含答案)2024-2025学年人教版数学八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 443.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-08 14:51:34 | ||
图片预览

文档简介
第十一章三角形单元测试2024-2025学年人教版数学八年级上册
一、单选题
1.下列长度的三条线段不能组成三角形的是( )
A.,, B.,,
C.,, D.,,
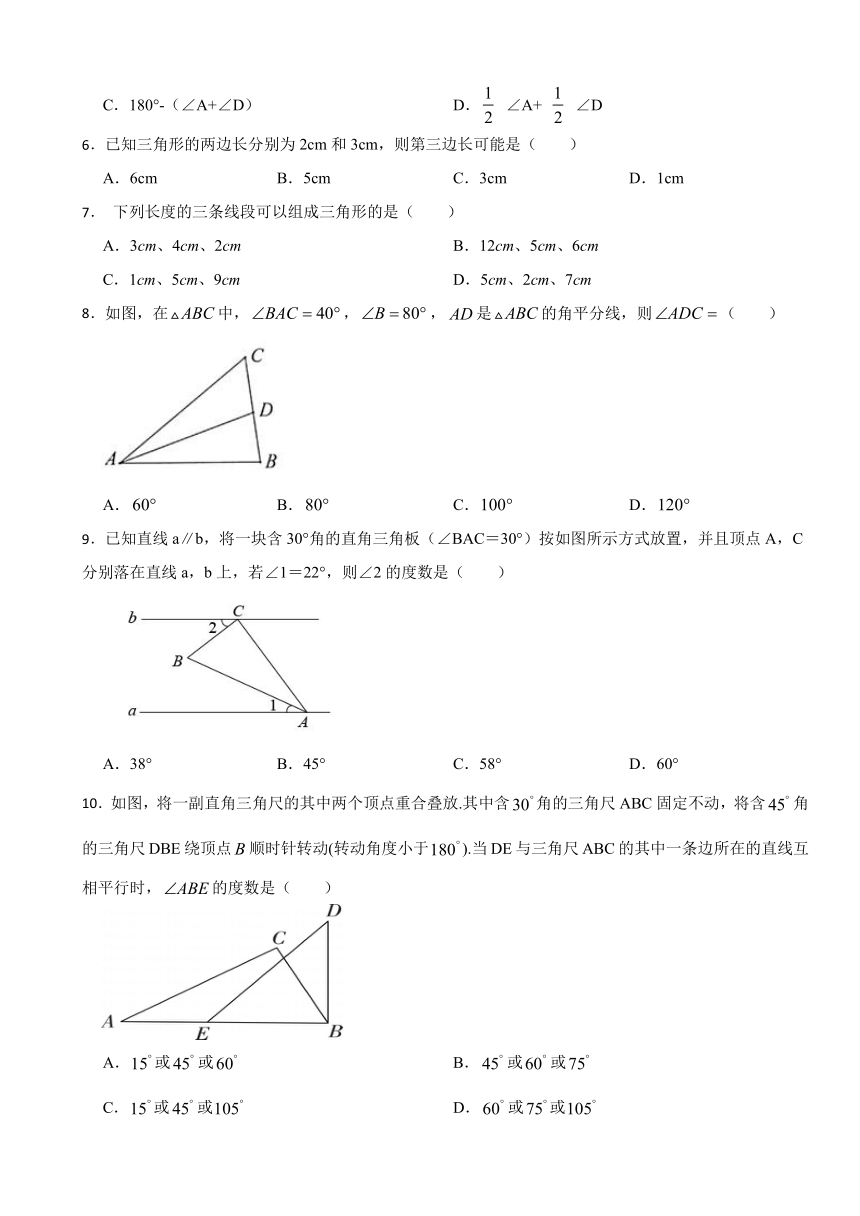
2.将一副直角三角板如图所示放置,使含 角的三角板的一条直角边和含 角的三角板的一条直角边在同一条直线上,则 的度数为( )
A. B. C. D.
3.直线a//b,其中∠1=20°, ∠2=36°,∠3为( )
A.56° B.124° C.34° D.36°
4.下列每组数分别是三根小木棒的长度,用它们能摆成三角形的是( )
A.3cm,4cm,8cm B.8cm,7cm,15cm
C.13cm,12cm,20cm D.5cm,5cm,11cm
5.如图,在四边形ABCD中,∠ABC与∠BCD的平分线的交点E恰好在AD边上,则∠BEC=( )
A.∠A+∠D-45° B. (∠A+∠D) +45°
C.180°-(∠A+∠D) D. ∠A+ ∠D
6.已知三角形的两边长分别为2cm和3cm,则第三边长可能是( )
A.6cm B.5cm C.3cm D.1cm
7. 下列长度的三条线段可以组成三角形的是( )
A.3cm、4cm、2cm B.12cm、5cm、6cm
C.1cm、5cm、9cm D.5cm、2cm、7cm
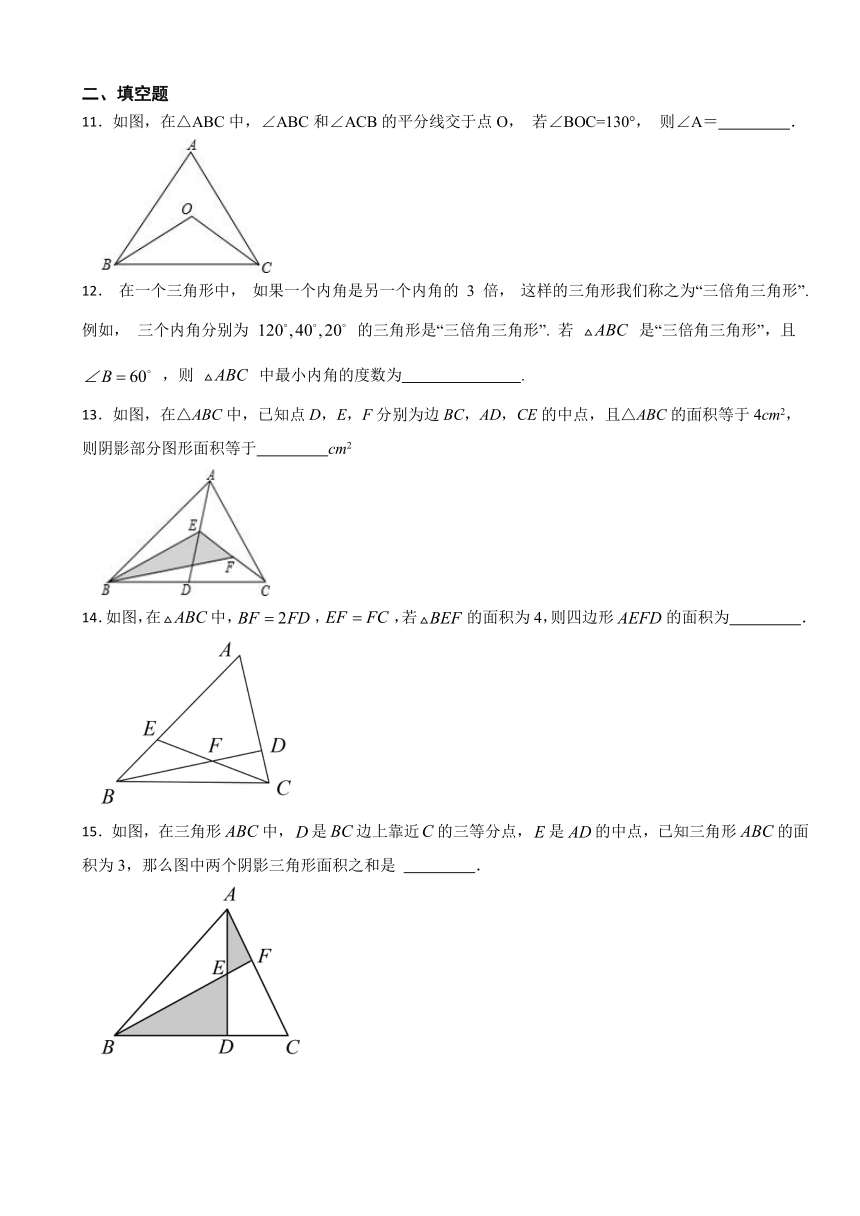
8.如图,在中,,,是的角平分线,则( )
A. B. C. D.
9.已知直线a∥b,将一块含30°角的直角三角板(∠BAC=30°)按如图所示方式放置,并且顶点A,C分别落在直线a,b上,若∠1=22°,则∠2的度数是( )
A.38° B.45° C.58° D.60°
10.如图,将一副直角三角尺的其中两个顶点重合叠放.其中含角的三角尺ABC固定不动,将含角的三角尺DBE绕顶点顺时针转动(转动角度小于).当DE与三角尺ABC的其中一条边所在的直线互相平行时,的度数是( )
A.或或 B.或或
C.或或 D.或或
二、填空题
11.如图,在△ABC中,∠ABC和∠ACB的平分线交于点O, 若∠BOC=130°, 则∠A= .
12. 在一个三角形中, 如果一个内角是另一个内角的 3 倍, 这样的三角形我们称之为“三倍角三角形”. 例如, 三个内角分别为 的三角形是“三倍角三角形”. 若 是“三倍角三角形”,且 ,则 中最小内角的度数为 .
13.如图,在△ABC中,已知点D,E,F分别为边BC,AD,CE的中点,且△ABC的面积等于4cm2,则阴影部分图形面积等于 cm2
14.如图,在中,,,若的面积为4,则四边形的面积为 .
15.如图,在三角形中,是边上靠近的三等分点,是的中点,已知三角形的面积为3,那么图中两个阴影三角形面积之和是 .
三、解答题
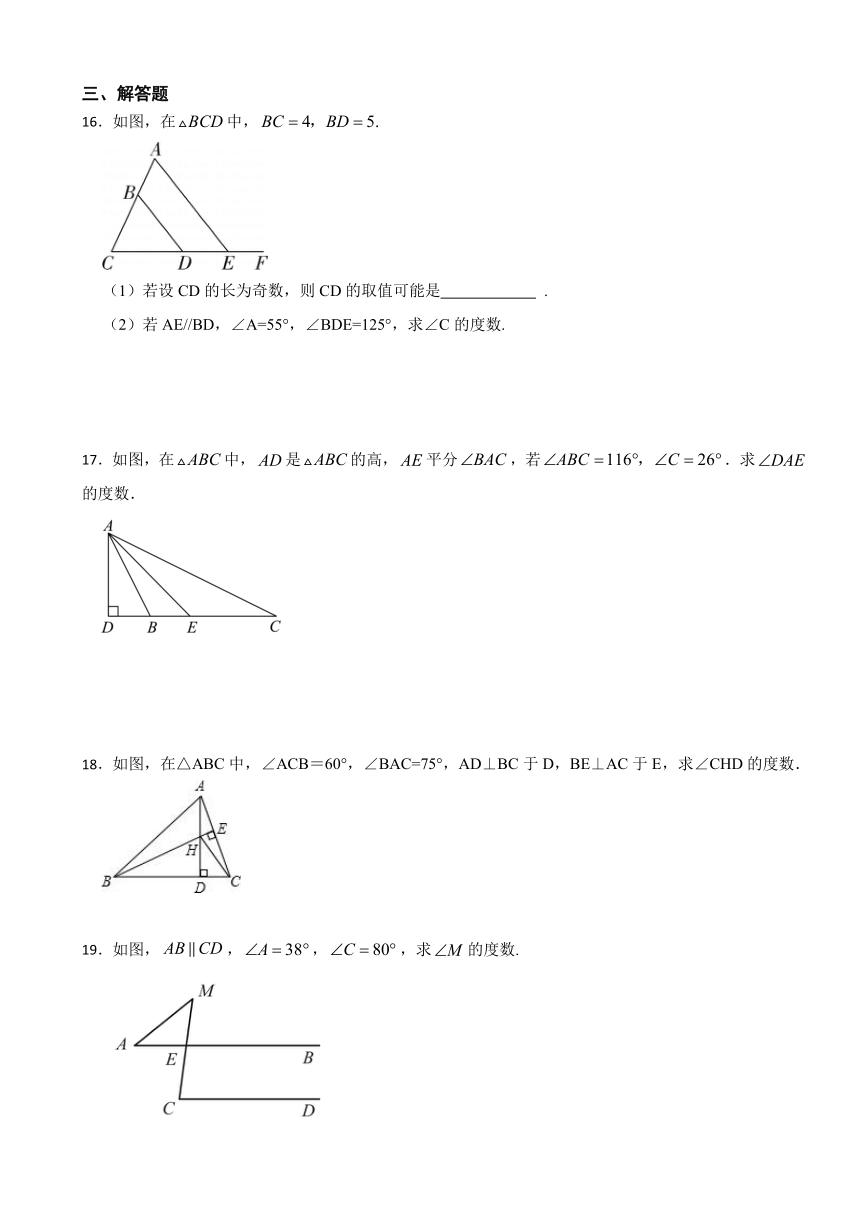
16.如图,在中,
(1)若设CD的长为奇数,则CD的取值可能是 .
(2)若AE//BD,∠A=55°,∠BDE=125°,求∠C的度数.
17.如图,在中,是的高,平分,若.求的度数.
18.如图,在△ABC中,∠ACB=60°,∠BAC=75°,AD⊥BC于D,BE⊥AC于E,求∠CHD的度数.
19.如图,,,,求的度数.
20.如图,在△ABC中,CE,BF是两条高,若∠A=70°,∠BCE=30°,求∠EBF与∠FBC的度数.
21.如图1,直线与直线、分别交于C,D两点,点M在直线上,射线平分交直线于点Q,.
(1)证明:;
(2)如图2,点P是上一点,射线交直线于点F,.
①若,直接写出的度数是 ▲ ;
②点N在射线上,满足,连接,请补全图形,探究与满足的等量关系,并证明.
答案解析部分
1.【答案】D
2.【答案】A
3.【答案】A
4.【答案】C
5.【答案】D
6.【答案】C
7.【答案】A
8.【答案】C
9.【答案】A
10.【答案】C
11.【答案】80°
12.【答案】20°或30°
13.【答案】1
14.【答案】14
15.【答案】
16.【答案】(1)3或5或7
(2)
17.【答案】.
18.【答案】解:延长CH交AB于F,
在△ABC中,三边的高交于一点,
∵∠BAC=75°,且CF⊥AB,
∵∠ACB=60°,
∴∠BCF=45°
在△CDH中,三内角之和为180°,
∴∠CHD=45°.
19.【答案】解:∵,,
∴,
∵,,
∴
20.【答案】解:在Rt△ABF中,∠A=70°,BF是两条高,
∴∠EBF=20°,∠ECA=20°,
又∵∠BCE=30°,
∴∠ACB=50°,
∴在Rt△BCF中∠FBC=40°.
21.【答案】(1)证明:平分,,
又,,,;
(2)解:①,
平分,,
又,,故答案为:;
②或,理由如下:
如图1,,,又,,
,;
如图2,由①可得
,,
,,
即:,
,
,
.
综上所述,与满足的等量关系为或.
一、单选题
1.下列长度的三条线段不能组成三角形的是( )
A.,, B.,,
C.,, D.,,
2.将一副直角三角板如图所示放置,使含 角的三角板的一条直角边和含 角的三角板的一条直角边在同一条直线上,则 的度数为( )
A. B. C. D.
3.直线a//b,其中∠1=20°, ∠2=36°,∠3为( )
A.56° B.124° C.34° D.36°
4.下列每组数分别是三根小木棒的长度,用它们能摆成三角形的是( )
A.3cm,4cm,8cm B.8cm,7cm,15cm
C.13cm,12cm,20cm D.5cm,5cm,11cm
5.如图,在四边形ABCD中,∠ABC与∠BCD的平分线的交点E恰好在AD边上,则∠BEC=( )
A.∠A+∠D-45° B. (∠A+∠D) +45°
C.180°-(∠A+∠D) D. ∠A+ ∠D
6.已知三角形的两边长分别为2cm和3cm,则第三边长可能是( )
A.6cm B.5cm C.3cm D.1cm
7. 下列长度的三条线段可以组成三角形的是( )
A.3cm、4cm、2cm B.12cm、5cm、6cm
C.1cm、5cm、9cm D.5cm、2cm、7cm
8.如图,在中,,,是的角平分线,则( )
A. B. C. D.
9.已知直线a∥b,将一块含30°角的直角三角板(∠BAC=30°)按如图所示方式放置,并且顶点A,C分别落在直线a,b上,若∠1=22°,则∠2的度数是( )
A.38° B.45° C.58° D.60°
10.如图,将一副直角三角尺的其中两个顶点重合叠放.其中含角的三角尺ABC固定不动,将含角的三角尺DBE绕顶点顺时针转动(转动角度小于).当DE与三角尺ABC的其中一条边所在的直线互相平行时,的度数是( )
A.或或 B.或或
C.或或 D.或或
二、填空题
11.如图,在△ABC中,∠ABC和∠ACB的平分线交于点O, 若∠BOC=130°, 则∠A= .
12. 在一个三角形中, 如果一个内角是另一个内角的 3 倍, 这样的三角形我们称之为“三倍角三角形”. 例如, 三个内角分别为 的三角形是“三倍角三角形”. 若 是“三倍角三角形”,且 ,则 中最小内角的度数为 .
13.如图,在△ABC中,已知点D,E,F分别为边BC,AD,CE的中点,且△ABC的面积等于4cm2,则阴影部分图形面积等于 cm2
14.如图,在中,,,若的面积为4,则四边形的面积为 .
15.如图,在三角形中,是边上靠近的三等分点,是的中点,已知三角形的面积为3,那么图中两个阴影三角形面积之和是 .
三、解答题
16.如图,在中,
(1)若设CD的长为奇数,则CD的取值可能是 .
(2)若AE//BD,∠A=55°,∠BDE=125°,求∠C的度数.
17.如图,在中,是的高,平分,若.求的度数.
18.如图,在△ABC中,∠ACB=60°,∠BAC=75°,AD⊥BC于D,BE⊥AC于E,求∠CHD的度数.
19.如图,,,,求的度数.
20.如图,在△ABC中,CE,BF是两条高,若∠A=70°,∠BCE=30°,求∠EBF与∠FBC的度数.
21.如图1,直线与直线、分别交于C,D两点,点M在直线上,射线平分交直线于点Q,.
(1)证明:;
(2)如图2,点P是上一点,射线交直线于点F,.
①若,直接写出的度数是 ▲ ;
②点N在射线上,满足,连接,请补全图形,探究与满足的等量关系,并证明.
答案解析部分
1.【答案】D
2.【答案】A
3.【答案】A
4.【答案】C
5.【答案】D
6.【答案】C
7.【答案】A
8.【答案】C
9.【答案】A
10.【答案】C
11.【答案】80°
12.【答案】20°或30°
13.【答案】1
14.【答案】14
15.【答案】
16.【答案】(1)3或5或7
(2)
17.【答案】.
18.【答案】解:延长CH交AB于F,
在△ABC中,三边的高交于一点,
∵∠BAC=75°,且CF⊥AB,
∵∠ACB=60°,
∴∠BCF=45°
在△CDH中,三内角之和为180°,
∴∠CHD=45°.
19.【答案】解:∵,,
∴,
∵,,
∴
20.【答案】解:在Rt△ABF中,∠A=70°,BF是两条高,
∴∠EBF=20°,∠ECA=20°,
又∵∠BCE=30°,
∴∠ACB=50°,
∴在Rt△BCF中∠FBC=40°.
21.【答案】(1)证明:平分,,
又,,,;
(2)解:①,
平分,,
又,,故答案为:;
②或,理由如下:
如图1,,,又,,
,;
如图2,由①可得
,,
,,
即:,
,
,
.
综上所述,与满足的等量关系为或.
