14.1勾股定理 华东师大版初中数学八年级上册同步练习(含详细答案解析)
文档属性
| 名称 | 14.1勾股定理 华东师大版初中数学八年级上册同步练习(含详细答案解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 705.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-08 16:04:26 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
14.1勾股定理华东师大版初中数学八年级上册同步练习
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.如图,在中,,平分,垂直平分,垂足为,若,则的长度为 ( )
A. B. C. D.
2.如图,已知在和中,,,,,,三点在同一条直线上,连接,有下列四个结论:;;;其中正确结论的个数为 ( )
A. B. C. D.
3.在中,,,,则不能作为判定是直角三角形的条件的是( )
A. B.
C. D.
4.如图,在中,,,是的角平分线,于点若,则的长为( )
A. B. C. D.
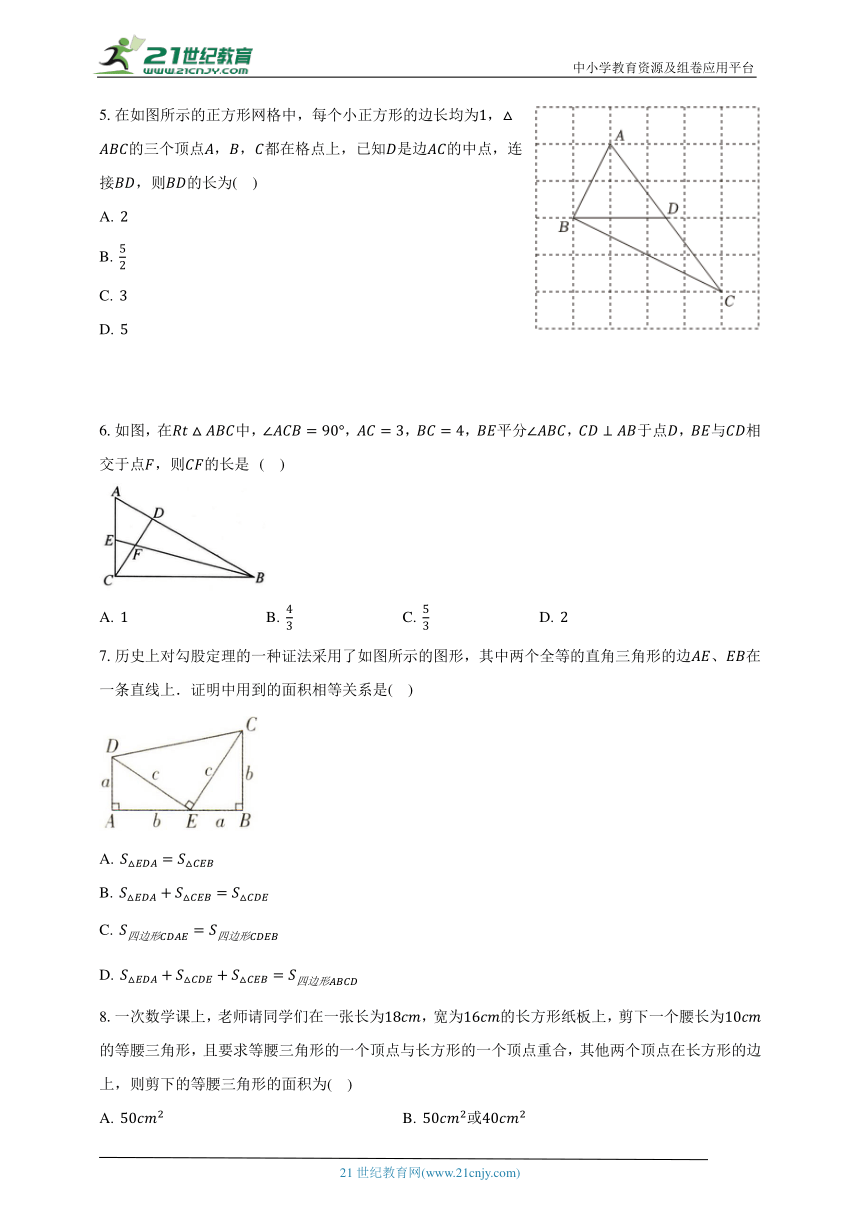
5.在如图所示的正方形网格中,每个小正方形的边长均为,的三个顶点,,都在格点上,已知是边的中点,连接,则的长为( )
A.
B.
C.
D.
6.如图,在中,,,,平分,于点,与相交于点,则的长是 ( )
A. B. C. D.
7.历史上对勾股定理的一种证法采用了如图所示的图形,其中两个全等的直角三角形的边、在一条直线上.证明中用到的面积相等关系是( )
A.
B.
C.
D.
8.一次数学课上,老师请同学们在一张长为,宽为的长方形纸板上,剪下一个腰长为的等腰三角形,且要求等腰三角形的一个顶点与长方形的一个顶点重合,其他两个顶点在长方形的边上,则剪下的等腰三角形的面积为( )
A. B. 或
C. 或或 D. 或或
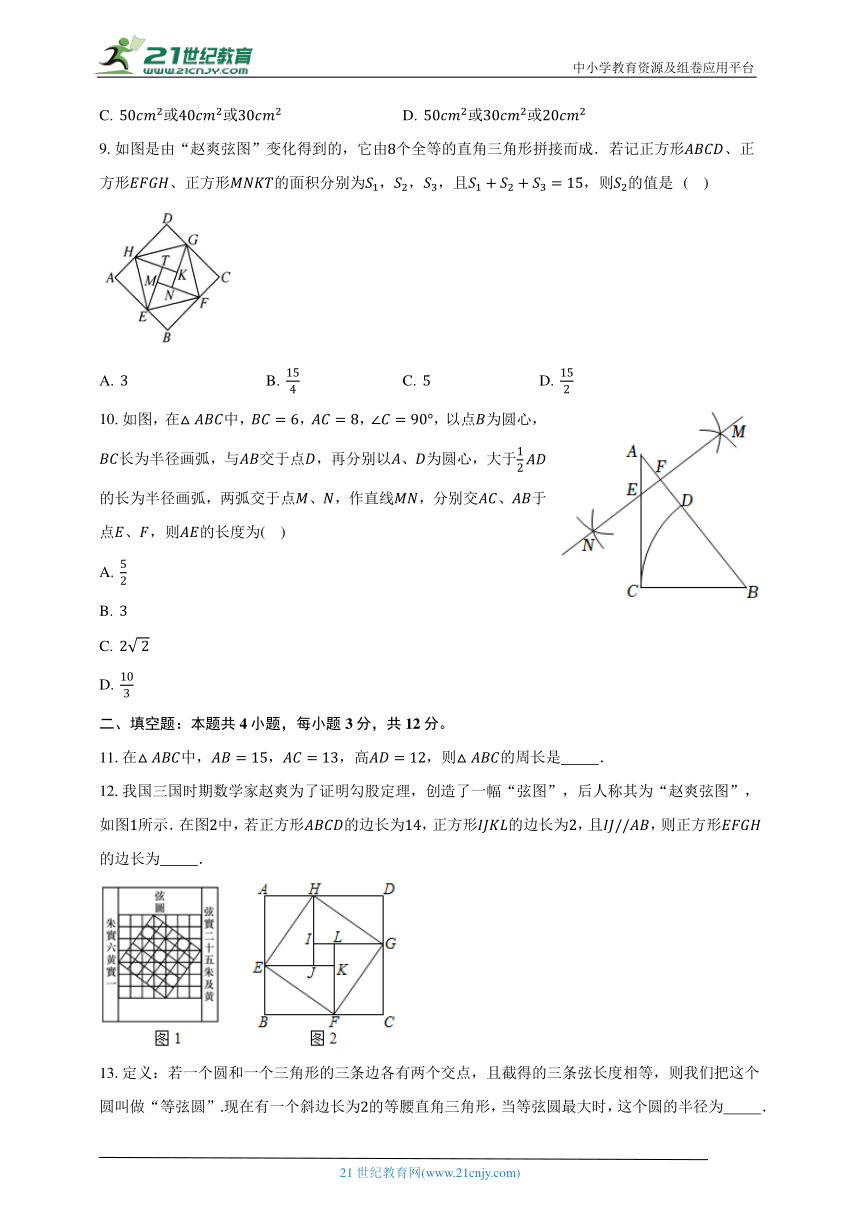
9.如图是由“赵爽弦图”变化得到的,它由个全等的直角三角形拼接而成.若记正方形、正方形、正方形的面积分别为,,,且,则的值是 ( )
A. B. C. D.
10.如图,在中,,,,以点为圆心,长为半径画弧,与交于点,再分别以、为圆心,大于的长为半径画弧,两弧交于点、,作直线,分别交、于点、,则的长度为( )
A.
B.
C.
D.
二、填空题:本题共4小题,每小题3分,共12分。
11.在中,,,高,则的周长是 .
12.我国三国时期数学家赵爽为了证明勾股定理,创造了一幅“弦图”,后人称其为“赵爽弦图”,如图所示.在图中,若正方形的边长为,正方形的边长为,且,则正方形的边长为 .
13.定义:若一个圆和一个三角形的三条边各有两个交点,且截得的三条弦长度相等,则我们把这个圆叫做“等弦圆”现在有一个斜边长为的等腰直角三角形,当等弦圆最大时,这个圆的半径为 .
14.如图,在四边形中,,,为的中点.若,,,则的长为 .
三、解答题:本题共6小题,共48分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
如图,在中,点是的中点,,连接,为上一点,,交于点,若,,求的长度.
16.本小题分
阅读下列题目的解题过程:
已知,,为三边的长,且满足,试判断的形状.
解:因为,
所以,
所以,
所以是直角三角形.
问:
上述解题过程,从第 填序号步开始出现错误;
错误的原因为 ;
本题正确的结论为 .
17.本小题分
已知方格纸中每个小正方形的边长均为,我们把以格点连线为边的多边形称为“格点多边形”.
在图中确定格点,画出一个以,,,为顶点的四边形,使其为轴对称图形.
在图中画出一个格点正方形,使其面积等于.
直接写出图中的面积是 .
18.本小题分
将沿折叠,使点刚好落在边上的点处,展开如图.
【操作观察】
如图,,.
;
若,则 ;
【理解应用】如图,若,求证:;
【拓展延伸】如图,,为的中点,且,是线段上的一个动点,连接,,求的最小值.
19.本小题分
如图,在的方格纸中,请按要求画格点线段端点在格点上,且线段的端点均不与点、、、重合.
在图中画格点线段、各一条,使点、、、分别落在边、、、上,且,不平行于;
在图中画格点线段、各一条,使点、、、分别落在边、、、上,且.
20.本小题分
如图,和都是等腰直角三角形,,,的顶点在的斜边上,连接.
求证:≌.
求证:.
如图,过点作于点并延长交于点,请写出线段,,之间的数量关系,并给出证明.
答案和解析
1.【答案】
【解析】解:平分,
,
垂直平分,
,
,
,
又,
,
解得,
设,则,
在中,,,
,即,
解得,即,
.
故选:.
先根据角平分线的定义、线段垂直平分线的性质、等腰三角形的性质可得,,再根据三角形的内角和定理可得,设,则,在中,根据含度角的直角三角形的性质即可得.
本题考查了线段垂直平分线的性质、等腰三角形的性质、含度角的直角三角形的性质等知识点,熟练掌握含度角的直角三角形的性质是解题关键.
2.【答案】
【解析】略
3.【答案】
【解析】解:、,,,能判定是直角三角形,故不符合题意;
B、,,即,根据勾股定理逆定理可判定是直角三角形,故不符合题意;
C、由::::可设,,,则有,根据勾股定理逆定理可判定是直角三角形,故不符合题意;
D、由::::可设,,,所以,解得,则,,,所以不能判定是直角三角形,故符合题意;
故选:.
根据三角形内角和及勾股定理可进行求解.
本题主要考查勾股定理逆定理和三角形内角和定理,熟练掌握勾股定理的逆定理是解题的关键.
4.【答案】
【解析】【分析】
本题主要考查角平分线的性质、全等三角形的判定和性质,掌握全等三角形的判定方法是解题的关键,即、、、和.
由角平分线的性质可得到,由等腰直角三角形可得,在中,由勾股定理可求得,可求得,则可求得;由证明≌,可得到,可求得的长.
【解答】
解:,,平分,
,
,
,
,
,
在中,由勾股定理可得,
,
.
在和中
≌,
,
.
5.【答案】
【解析】解:,,,
,
,
是边上的中线,
,
故选:.
根据勾股定理求出各边长度,根据勾股定理的逆定理判断出,利用直角三角形斜边上的中线等于斜边的一半即可得到结论.
本题考查了勾股定理及其逆定理,直角三角形的性质,熟练掌握直角三角形斜边上的中线等于斜边的一半即可得到结论.
6.【答案】
【解析】 提示:过点作于点因为于点,所以,所以因为,所以又因为平分,,所以在中,,,,所以易证≌,所以,所以,,所以设,则在中,由勾股定理,得,解得所以的长是.
7.【答案】
【解析】略
8.【答案】
【解析】本题可分三种情况讨论:如图,中,,;如图,中,,在中,,根据勾股定理可得,;如图,中,,在中,,根据勾股定理可得,故选C.
9.【答案】
【解析】提示:因为个直角三角形全等,四边形、四边形、四边形是正方形,所以,所以.,所以,所以,所以.
10.【答案】
【解析】解:在中,,,
,
,
,
由作图可知垂直平分线段,
,
,,
∽,
,
,
,
故选:.
利用勾股定理求出,再利用相似三角形的性质求出即可.
本题考查勾股定理,相似三角形的判定和性质等知识,解题的关键是正确寻找相似三角形解决问题,属于中考常考题型.
11.【答案】或
【解析】【分析】
本题考查了勾股定理以及分类讨论,熟练掌握勾股定理的应用与分类讨论是解题关键分为锐角三角形时和钝角三角形时解答即可.
【解答】
解:此题应分两种情况说明:
如图,当为锐角三角形时,
在中, ,
在中, ,,
,
的周长为
如图,当为钝角三角形时,
同理,在中, ,
在中,,
.
的周长为.
综上所述,的周长是或.
12.【答案】
【解析】【分析】
本题主要考查了勾股定理的证明,关键是熟练掌握正方形面积公式,以及面积的和差关系,难点是得到正方形的面积.
根据正方形面积公式,由面积的和差关系可得个直角三角形的面积,进一步得到个直角三角形的面积,再由面积的和差关系可得正方形的面积,进一步求出正方形的边长.
【解答】
解:每个直角三角形的面积是
,
正方形的面积是
,
则正方形的边长为.
答:正方形的边长为.
故答案为:.
13.【答案】
【解析】如图,当经过直角顶点时,最大,连接,过点分别作,,,垂足分别为,,由题意,得,所以由勾股定理,易证,即平分所以,即,,三点共线.因为是等腰直角三角形,所以,又,所以设的半径为,则又,所以,即所以在中,由勾股定理,得,所以,即所以又,所以,解得则这个圆的半径为.
14.【答案】
【解析】延长交于点因为,所以因为,所以,,因为为的中点,所以在和中,所以≌,所以,因为,所以因为,所以因为,所以,所以.
15.【答案】解:点是的中点,,
,
,
,
,
,
,
,
,
.
【解析】根据题意可得,根据先求出,再结合推出,即可求解.
本题考查了等腰三角形的性质以及勾股定理的应用,解答本题的关键是熟练掌握勾股定理:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.
16.【答案】【小题】
【小题】
没有考虑
【小题】
是直角三角形或等腰三角形.
【解析】 略
略
略
17.【答案】【小题】
解:如图所示答案不唯一.
【小题】
如图所示.
【小题】
【解析】 略
略
略
18.【答案】【小题】
【小题】
由折叠的性质,得,,因为,所以因为,所以,所以,所以,所以.
【小题】
连接,,由折叠的性质,得,,所以,即的最小值为的长.因为,所以是等边三角形.因为为的中点,,所以,,所以,所以,所以的最小值为,所以的最小值为.
【解析】 略
略
略
19.【答案】【小题】
如图,线段、即为所求
【小题】
如图,线段、即为所求
【解析】 略
略
20.【答案】【小题】
证明:因为,即,所以在和中,所以≌.
【小题】
证明:因为≌,所以,又因为,所以在中,根据勾股定理,得在中,根据勾股定理,得又因为,,所以.
【小题】
解:证明如下: 连接由,得,因为,,所以所以是的垂直平分线,所以在中,根据勾股定理,得,所以.
【解析】 略
略
略
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
14.1勾股定理华东师大版初中数学八年级上册同步练习
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.如图,在中,,平分,垂直平分,垂足为,若,则的长度为 ( )
A. B. C. D.
2.如图,已知在和中,,,,,,三点在同一条直线上,连接,有下列四个结论:;;;其中正确结论的个数为 ( )
A. B. C. D.
3.在中,,,,则不能作为判定是直角三角形的条件的是( )
A. B.
C. D.
4.如图,在中,,,是的角平分线,于点若,则的长为( )
A. B. C. D.
5.在如图所示的正方形网格中,每个小正方形的边长均为,的三个顶点,,都在格点上,已知是边的中点,连接,则的长为( )
A.
B.
C.
D.
6.如图,在中,,,,平分,于点,与相交于点,则的长是 ( )
A. B. C. D.
7.历史上对勾股定理的一种证法采用了如图所示的图形,其中两个全等的直角三角形的边、在一条直线上.证明中用到的面积相等关系是( )
A.
B.
C.
D.
8.一次数学课上,老师请同学们在一张长为,宽为的长方形纸板上,剪下一个腰长为的等腰三角形,且要求等腰三角形的一个顶点与长方形的一个顶点重合,其他两个顶点在长方形的边上,则剪下的等腰三角形的面积为( )
A. B. 或
C. 或或 D. 或或
9.如图是由“赵爽弦图”变化得到的,它由个全等的直角三角形拼接而成.若记正方形、正方形、正方形的面积分别为,,,且,则的值是 ( )
A. B. C. D.
10.如图,在中,,,,以点为圆心,长为半径画弧,与交于点,再分别以、为圆心,大于的长为半径画弧,两弧交于点、,作直线,分别交、于点、,则的长度为( )
A.
B.
C.
D.
二、填空题:本题共4小题,每小题3分,共12分。
11.在中,,,高,则的周长是 .
12.我国三国时期数学家赵爽为了证明勾股定理,创造了一幅“弦图”,后人称其为“赵爽弦图”,如图所示.在图中,若正方形的边长为,正方形的边长为,且,则正方形的边长为 .
13.定义:若一个圆和一个三角形的三条边各有两个交点,且截得的三条弦长度相等,则我们把这个圆叫做“等弦圆”现在有一个斜边长为的等腰直角三角形,当等弦圆最大时,这个圆的半径为 .
14.如图,在四边形中,,,为的中点.若,,,则的长为 .
三、解答题:本题共6小题,共48分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
如图,在中,点是的中点,,连接,为上一点,,交于点,若,,求的长度.
16.本小题分
阅读下列题目的解题过程:
已知,,为三边的长,且满足,试判断的形状.
解:因为,
所以,
所以,
所以是直角三角形.
问:
上述解题过程,从第 填序号步开始出现错误;
错误的原因为 ;
本题正确的结论为 .
17.本小题分
已知方格纸中每个小正方形的边长均为,我们把以格点连线为边的多边形称为“格点多边形”.
在图中确定格点,画出一个以,,,为顶点的四边形,使其为轴对称图形.
在图中画出一个格点正方形,使其面积等于.
直接写出图中的面积是 .
18.本小题分
将沿折叠,使点刚好落在边上的点处,展开如图.
【操作观察】
如图,,.
;
若,则 ;
【理解应用】如图,若,求证:;
【拓展延伸】如图,,为的中点,且,是线段上的一个动点,连接,,求的最小值.
19.本小题分
如图,在的方格纸中,请按要求画格点线段端点在格点上,且线段的端点均不与点、、、重合.
在图中画格点线段、各一条,使点、、、分别落在边、、、上,且,不平行于;
在图中画格点线段、各一条,使点、、、分别落在边、、、上,且.
20.本小题分
如图,和都是等腰直角三角形,,,的顶点在的斜边上,连接.
求证:≌.
求证:.
如图,过点作于点并延长交于点,请写出线段,,之间的数量关系,并给出证明.
答案和解析
1.【答案】
【解析】解:平分,
,
垂直平分,
,
,
,
又,
,
解得,
设,则,
在中,,,
,即,
解得,即,
.
故选:.
先根据角平分线的定义、线段垂直平分线的性质、等腰三角形的性质可得,,再根据三角形的内角和定理可得,设,则,在中,根据含度角的直角三角形的性质即可得.
本题考查了线段垂直平分线的性质、等腰三角形的性质、含度角的直角三角形的性质等知识点,熟练掌握含度角的直角三角形的性质是解题关键.
2.【答案】
【解析】略
3.【答案】
【解析】解:、,,,能判定是直角三角形,故不符合题意;
B、,,即,根据勾股定理逆定理可判定是直角三角形,故不符合题意;
C、由::::可设,,,则有,根据勾股定理逆定理可判定是直角三角形,故不符合题意;
D、由::::可设,,,所以,解得,则,,,所以不能判定是直角三角形,故符合题意;
故选:.
根据三角形内角和及勾股定理可进行求解.
本题主要考查勾股定理逆定理和三角形内角和定理,熟练掌握勾股定理的逆定理是解题的关键.
4.【答案】
【解析】【分析】
本题主要考查角平分线的性质、全等三角形的判定和性质,掌握全等三角形的判定方法是解题的关键,即、、、和.
由角平分线的性质可得到,由等腰直角三角形可得,在中,由勾股定理可求得,可求得,则可求得;由证明≌,可得到,可求得的长.
【解答】
解:,,平分,
,
,
,
,
,
在中,由勾股定理可得,
,
.
在和中
≌,
,
.
5.【答案】
【解析】解:,,,
,
,
是边上的中线,
,
故选:.
根据勾股定理求出各边长度,根据勾股定理的逆定理判断出,利用直角三角形斜边上的中线等于斜边的一半即可得到结论.
本题考查了勾股定理及其逆定理,直角三角形的性质,熟练掌握直角三角形斜边上的中线等于斜边的一半即可得到结论.
6.【答案】
【解析】 提示:过点作于点因为于点,所以,所以因为,所以又因为平分,,所以在中,,,,所以易证≌,所以,所以,,所以设,则在中,由勾股定理,得,解得所以的长是.
7.【答案】
【解析】略
8.【答案】
【解析】本题可分三种情况讨论:如图,中,,;如图,中,,在中,,根据勾股定理可得,;如图,中,,在中,,根据勾股定理可得,故选C.
9.【答案】
【解析】提示:因为个直角三角形全等,四边形、四边形、四边形是正方形,所以,所以.,所以,所以,所以.
10.【答案】
【解析】解:在中,,,
,
,
,
由作图可知垂直平分线段,
,
,,
∽,
,
,
,
故选:.
利用勾股定理求出,再利用相似三角形的性质求出即可.
本题考查勾股定理,相似三角形的判定和性质等知识,解题的关键是正确寻找相似三角形解决问题,属于中考常考题型.
11.【答案】或
【解析】【分析】
本题考查了勾股定理以及分类讨论,熟练掌握勾股定理的应用与分类讨论是解题关键分为锐角三角形时和钝角三角形时解答即可.
【解答】
解:此题应分两种情况说明:
如图,当为锐角三角形时,
在中, ,
在中, ,,
,
的周长为
如图,当为钝角三角形时,
同理,在中, ,
在中,,
.
的周长为.
综上所述,的周长是或.
12.【答案】
【解析】【分析】
本题主要考查了勾股定理的证明,关键是熟练掌握正方形面积公式,以及面积的和差关系,难点是得到正方形的面积.
根据正方形面积公式,由面积的和差关系可得个直角三角形的面积,进一步得到个直角三角形的面积,再由面积的和差关系可得正方形的面积,进一步求出正方形的边长.
【解答】
解:每个直角三角形的面积是
,
正方形的面积是
,
则正方形的边长为.
答:正方形的边长为.
故答案为:.
13.【答案】
【解析】如图,当经过直角顶点时,最大,连接,过点分别作,,,垂足分别为,,由题意,得,所以由勾股定理,易证,即平分所以,即,,三点共线.因为是等腰直角三角形,所以,又,所以设的半径为,则又,所以,即所以在中,由勾股定理,得,所以,即所以又,所以,解得则这个圆的半径为.
14.【答案】
【解析】延长交于点因为,所以因为,所以,,因为为的中点,所以在和中,所以≌,所以,因为,所以因为,所以因为,所以,所以.
15.【答案】解:点是的中点,,
,
,
,
,
,
,
,
,
.
【解析】根据题意可得,根据先求出,再结合推出,即可求解.
本题考查了等腰三角形的性质以及勾股定理的应用,解答本题的关键是熟练掌握勾股定理:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.
16.【答案】【小题】
【小题】
没有考虑
【小题】
是直角三角形或等腰三角形.
【解析】 略
略
略
17.【答案】【小题】
解:如图所示答案不唯一.
【小题】
如图所示.
【小题】
【解析】 略
略
略
18.【答案】【小题】
【小题】
由折叠的性质,得,,因为,所以因为,所以,所以,所以,所以.
【小题】
连接,,由折叠的性质,得,,所以,即的最小值为的长.因为,所以是等边三角形.因为为的中点,,所以,,所以,所以,所以的最小值为,所以的最小值为.
【解析】 略
略
略
19.【答案】【小题】
如图,线段、即为所求
【小题】
如图,线段、即为所求
【解析】 略
略
20.【答案】【小题】
证明:因为,即,所以在和中,所以≌.
【小题】
证明:因为≌,所以,又因为,所以在中,根据勾股定理,得在中,根据勾股定理,得又因为,,所以.
【小题】
解:证明如下: 连接由,得,因为,,所以所以是的垂直平分线,所以在中,根据勾股定理,得,所以.
【解析】 略
略
略
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
