1.5 有理数的大小比较 课件(共23张PPT)
文档属性
| 名称 | 1.5 有理数的大小比较 课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-08 19:12:26 | ||
图片预览







文档简介
(共23张PPT)
第一章 有理数
1.5 有理数的大小比较
01
教学目标
02
课前回顾
03
新知讲解
04
典例分析
05
课堂练习
06
课堂小结
07
板书设计
01
教学目标
教学目标
1.掌握有理数大小的比较方法,会利用绝对值比较两个负数的大小.
2.学会利用各种方法比较有理数的大小,培养逻辑思维能力.
3.通过有理数大小比较的探究活动,培养学生观察和动手操作的能力.
教学重难点
重点:正确理解绝对值的意义,会利用绝对值比较两个负数大小.
难点:利用绝对值比较两个异分母负分数的大小.
02
课前回顾
1)求下列各数的绝对值:
-4.5,1.5,|-2.2|,-150%,0,-(-4).
2)在数轴上表示上面这些数,并按“<”排列.
03
新知讲解
下面是某一天5个城市的最低气温:
长沙5 ℃ 、哈尔滨-20 ℃、北京-10 ℃ 、广州10 ℃ 、上海0 ℃.
1)你能将上述五个城市的最低气温按从低到高的顺序依次排列吗?
2)你能在数轴表示各城市的最低温度吗?
哈尔滨-20 ℃<北京-10 ℃<上海0 ℃<长沙5 ℃<广州10 ℃
0
-20
-10
10
5
哈尔滨
(-20℃)
北京
(-10℃)
上海
(0℃ )
广州
(10℃ )
武汉(5 ℃ )
03
新知讲解
3)温度的高低与相应的数在数轴上的位置有什么关系?
在数轴上表示的两个数,右边的数总比左边的数大。
03
新知讲解
通过前面的学习,我们知道数轴上的两个有理数,_______的总比________的大,正数都大于______,负数都小于______,正数______负数.那么如何通过绝对值来比较有理数的大小呢?
右边
左边
0
0
大于
03
新知讲解
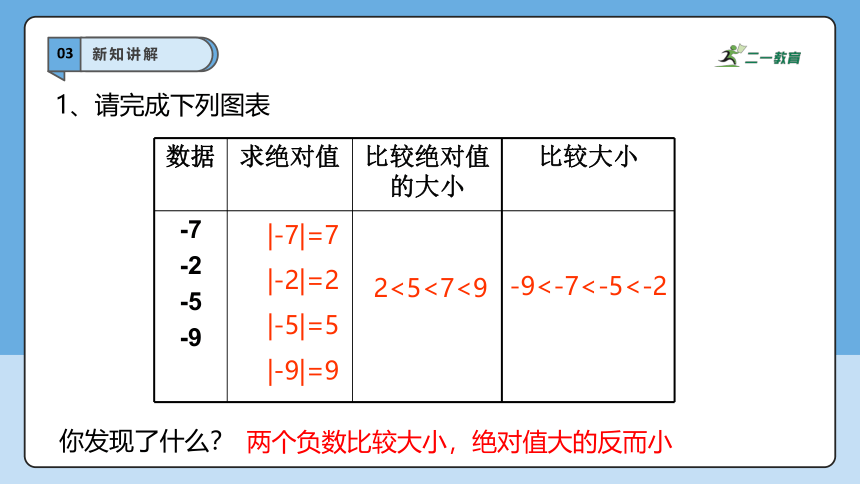
1、请完成下列图表
数据 求绝对值 比较绝对值 的大小 比较大小
8 2 15 1
1<2<8<15
|8|=8
|2|=2
|15|=15
|1|=1
1<2<8<15
你发现了什么?
正数比较大小,绝对值大的数大
03
新知讲解
你发现了什么?
两个负数比较大小,绝对值大的反而小
数据 求绝对值 比较绝对值的大小 比较大小
-7 -2 -5 -9
-9<-7<-5<-2
|-7|=7
|-2|=2
|-5|=5
|-9|=9
2<5<7<9
1、请完成下列图表
03
新知讲解
【提问】你能借助数轴说明为什么两个负数比较大小,绝对值大的反而小?
【理由】表示两个负数的点都位于原点的左边,绝对值大表示离原点远,所以绝对值大的那个负数反而小.故比较两个负数,可以先比较它们的绝对值的大小.
03
新知讲解
比较有理数大小的法则
1.一个数与0比较,要考虑这个数的正负.
正数>0>负数.
2.异号两数比较,要考虑这两个数的正负.
正数大于负数.
3.同号两数比较,要考虑这两个数的绝对值.
对于两个正数,绝对值大的数大.
对于两个负数,绝对值大的数反而小.
注意:需要化简时,要先化简再比较.
03
典例分析
例1 比较下列各数的大小
1)–(-1)和–(+2);
2) - 和-
3) -和|- |
1)解:先化简,–(-1)=1,–(+2)=-2
而1>-2,所以–(-1)>–(+2)。
2)这是两个负数比较大小,先求它们的绝对值。
|-|= ,|-|= =
而< , 即|-| < |-|
所以 -> -
3)先化简-=0.3, |- |=
而0.3< ,所以-< |- |
03
典例分析
1、比较下列每对数的大小。
解:
03
典例分析
【小结】比较两个负数大小的方法及其步骤:
1)先分别求出两个负数的绝对值;
2)比较两个绝对值的大小;
3)根据“两个负数,绝对值大的反而小”进行判断.
05
课堂练习
1.下列各式中正确的是( )
A.-5>-1 B.+(-8)>-(+3)
C.-|-4|>-|-1| D.-(-7)>-(-2)
2.在-6,-1,0,2中,最小的数是( )
A.-6 B.-1 C.0 D.2
D
A
05
课堂练习
3.比较下面各对数的大小,并说明理由:
(1) ____ ; (2)-3 ____+1;
(3)-1 ____ 0; (4)- ____- ;
(5)-|-3| ____-4.5
>
<
<
<
>
05
课堂练习
4.如图所示的四个数轴上的点A都表示有理数a,其中,一定满足|a|>|-2|的是( )
A.①③ B.②③ C.①④ D.②④
B
5.已知a<0,b>0,且|a|>|b|,则a、b、-a、-b的大小关系是( )
A.b>-a>a>-b B.-b>a>-a>b
C.a>-b>-a>b D.-a>b>-b>a
D
05
课堂练习
7.定义:对于任意数a,符号[a]表示不大于a的最大整数,例如:[5.8]=5,[10]=10,[-π]=-4.若[a]=-6,则a的取值范围是( )
A.a≥-6 B.-6≤a<-5
C.-6<a<-5 D.-7<a≤-6
B
6 .有理数a,b在数轴上的对应点的位置如图所示,则a,b,-a,|b|的大小关系正确的是( )
A.|b|>a>-a>b B.|b|>b>a>-a
C.a>|b|>b>-a D.a>|b|>-a>b
A
05
课堂练习
8.已知,,求,的值,并比较它们的大小.
【详解】解:,,
,.
当时,;
当时,.
06
课堂小结
07
板书设计
第1章 有理数
1.5 有理数的大小比较
1.两个负数比较大小
法则:两个负数,绝对值大的反而小.
2.有理数比较大小的方法
方法一:在数轴上把这些数表示出来,然后根据“数轴上右边的数总比左边的数大”来比较;
方法二:利用比较法则:“正数都大于零;负数都小于零;正数大于负数;两个负数,绝对值大的反而小”来进行.
Thanks!
https://www.21cnjy.com/recruitment/home/fine
第一章 有理数
1.5 有理数的大小比较
01
教学目标
02
课前回顾
03
新知讲解
04
典例分析
05
课堂练习
06
课堂小结
07
板书设计
01
教学目标
教学目标
1.掌握有理数大小的比较方法,会利用绝对值比较两个负数的大小.
2.学会利用各种方法比较有理数的大小,培养逻辑思维能力.
3.通过有理数大小比较的探究活动,培养学生观察和动手操作的能力.
教学重难点
重点:正确理解绝对值的意义,会利用绝对值比较两个负数大小.
难点:利用绝对值比较两个异分母负分数的大小.
02
课前回顾
1)求下列各数的绝对值:
-4.5,1.5,|-2.2|,-150%,0,-(-4).
2)在数轴上表示上面这些数,并按“<”排列.
03
新知讲解
下面是某一天5个城市的最低气温:
长沙5 ℃ 、哈尔滨-20 ℃、北京-10 ℃ 、广州10 ℃ 、上海0 ℃.
1)你能将上述五个城市的最低气温按从低到高的顺序依次排列吗?
2)你能在数轴表示各城市的最低温度吗?
哈尔滨-20 ℃<北京-10 ℃<上海0 ℃<长沙5 ℃<广州10 ℃
0
-20
-10
10
5
哈尔滨
(-20℃)
北京
(-10℃)
上海
(0℃ )
广州
(10℃ )
武汉(5 ℃ )
03
新知讲解
3)温度的高低与相应的数在数轴上的位置有什么关系?
在数轴上表示的两个数,右边的数总比左边的数大。
03
新知讲解
通过前面的学习,我们知道数轴上的两个有理数,_______的总比________的大,正数都大于______,负数都小于______,正数______负数.那么如何通过绝对值来比较有理数的大小呢?
右边
左边
0
0
大于
03
新知讲解
1、请完成下列图表
数据 求绝对值 比较绝对值 的大小 比较大小
8 2 15 1
1<2<8<15
|8|=8
|2|=2
|15|=15
|1|=1
1<2<8<15
你发现了什么?
正数比较大小,绝对值大的数大
03
新知讲解
你发现了什么?
两个负数比较大小,绝对值大的反而小
数据 求绝对值 比较绝对值的大小 比较大小
-7 -2 -5 -9
-9<-7<-5<-2
|-7|=7
|-2|=2
|-5|=5
|-9|=9
2<5<7<9
1、请完成下列图表
03
新知讲解
【提问】你能借助数轴说明为什么两个负数比较大小,绝对值大的反而小?
【理由】表示两个负数的点都位于原点的左边,绝对值大表示离原点远,所以绝对值大的那个负数反而小.故比较两个负数,可以先比较它们的绝对值的大小.
03
新知讲解
比较有理数大小的法则
1.一个数与0比较,要考虑这个数的正负.
正数>0>负数.
2.异号两数比较,要考虑这两个数的正负.
正数大于负数.
3.同号两数比较,要考虑这两个数的绝对值.
对于两个正数,绝对值大的数大.
对于两个负数,绝对值大的数反而小.
注意:需要化简时,要先化简再比较.
03
典例分析
例1 比较下列各数的大小
1)–(-1)和–(+2);
2) - 和-
3) -和|- |
1)解:先化简,–(-1)=1,–(+2)=-2
而1>-2,所以–(-1)>–(+2)。
2)这是两个负数比较大小,先求它们的绝对值。
|-|= ,|-|= =
而< , 即|-| < |-|
所以 -> -
3)先化简-=0.3, |- |=
而0.3< ,所以-< |- |
03
典例分析
1、比较下列每对数的大小。
解:
03
典例分析
【小结】比较两个负数大小的方法及其步骤:
1)先分别求出两个负数的绝对值;
2)比较两个绝对值的大小;
3)根据“两个负数,绝对值大的反而小”进行判断.
05
课堂练习
1.下列各式中正确的是( )
A.-5>-1 B.+(-8)>-(+3)
C.-|-4|>-|-1| D.-(-7)>-(-2)
2.在-6,-1,0,2中,最小的数是( )
A.-6 B.-1 C.0 D.2
D
A
05
课堂练习
3.比较下面各对数的大小,并说明理由:
(1) ____ ; (2)-3 ____+1;
(3)-1 ____ 0; (4)- ____- ;
(5)-|-3| ____-4.5
>
<
<
<
>
05
课堂练习
4.如图所示的四个数轴上的点A都表示有理数a,其中,一定满足|a|>|-2|的是( )
A.①③ B.②③ C.①④ D.②④
B
5.已知a<0,b>0,且|a|>|b|,则a、b、-a、-b的大小关系是( )
A.b>-a>a>-b B.-b>a>-a>b
C.a>-b>-a>b D.-a>b>-b>a
D
05
课堂练习
7.定义:对于任意数a,符号[a]表示不大于a的最大整数,例如:[5.8]=5,[10]=10,[-π]=-4.若[a]=-6,则a的取值范围是( )
A.a≥-6 B.-6≤a<-5
C.-6<a<-5 D.-7<a≤-6
B
6 .有理数a,b在数轴上的对应点的位置如图所示,则a,b,-a,|b|的大小关系正确的是( )
A.|b|>a>-a>b B.|b|>b>a>-a
C.a>|b|>b>-a D.a>|b|>-a>b
A
05
课堂练习
8.已知,,求,的值,并比较它们的大小.
【详解】解:,,
,.
当时,;
当时,.
06
课堂小结
07
板书设计
第1章 有理数
1.5 有理数的大小比较
1.两个负数比较大小
法则:两个负数,绝对值大的反而小.
2.有理数比较大小的方法
方法一:在数轴上把这些数表示出来,然后根据“数轴上右边的数总比左边的数大”来比较;
方法二:利用比较法则:“正数都大于零;负数都小于零;正数大于负数;两个负数,绝对值大的反而小”来进行.
Thanks!
https://www.21cnjy.com/recruitment/home/fine
同课章节目录
