人教版四年级下册数学 三角形的三边关系 课件(共31张PPT)
文档属性
| 名称 | 人教版四年级下册数学 三角形的三边关系 课件(共31张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 60.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-08 18:35:27 | ||
图片预览







文档简介
(共31张PPT)
三角形的三边关系(第三课时)
3.直尺、圆规、铅笔、橡皮
等文具。
1.学习任务单。
2.若干根长短不同的小棒。
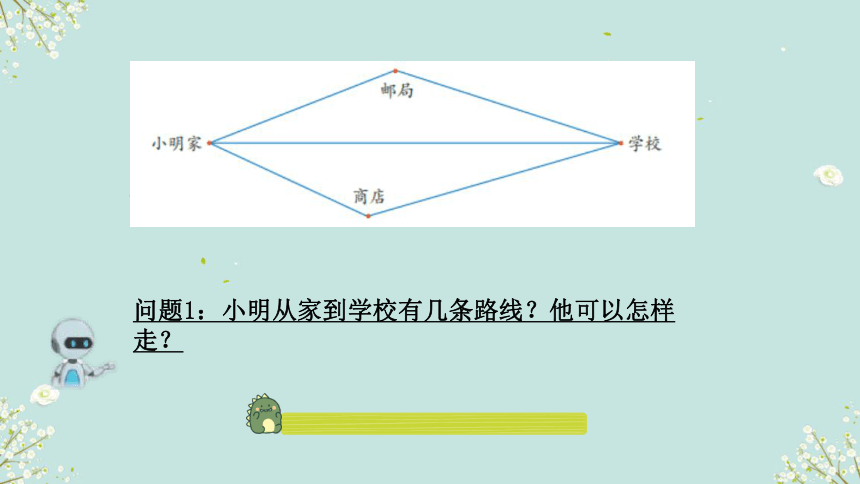
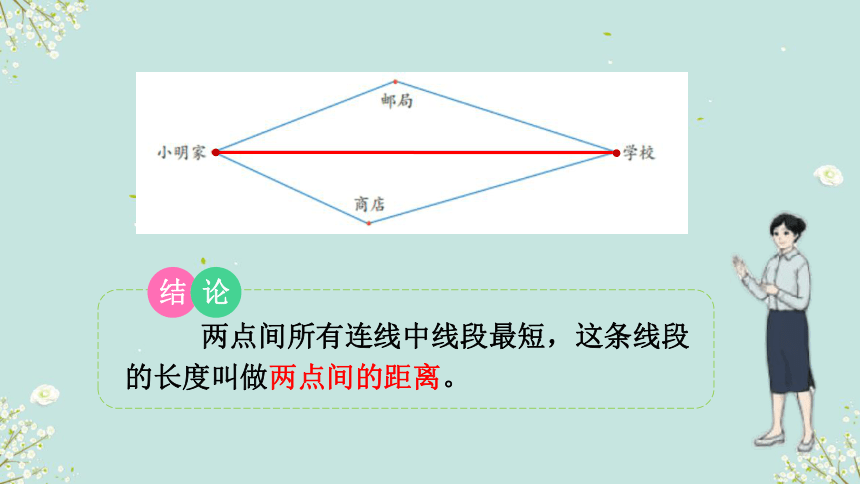
问题1:小明从家到学校有几条路线?他可以怎样走?
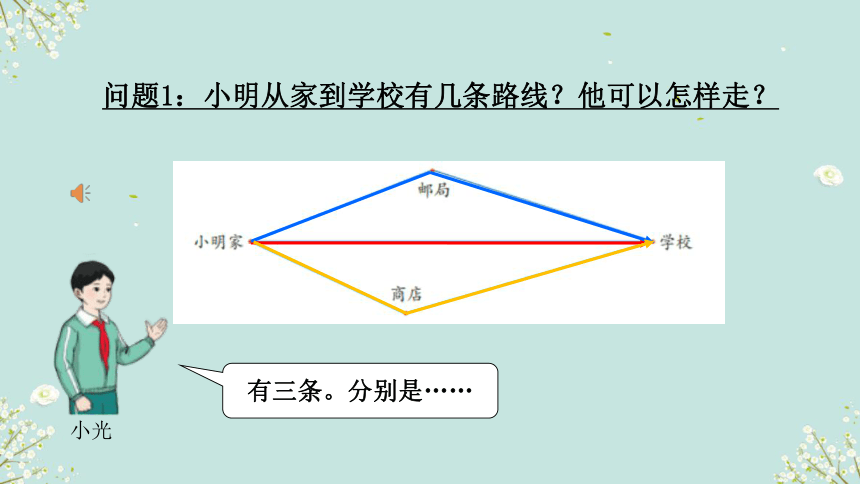
问题1:小明从家到学校有几条路线?他可以怎样走?
小光
有三条。分别是……
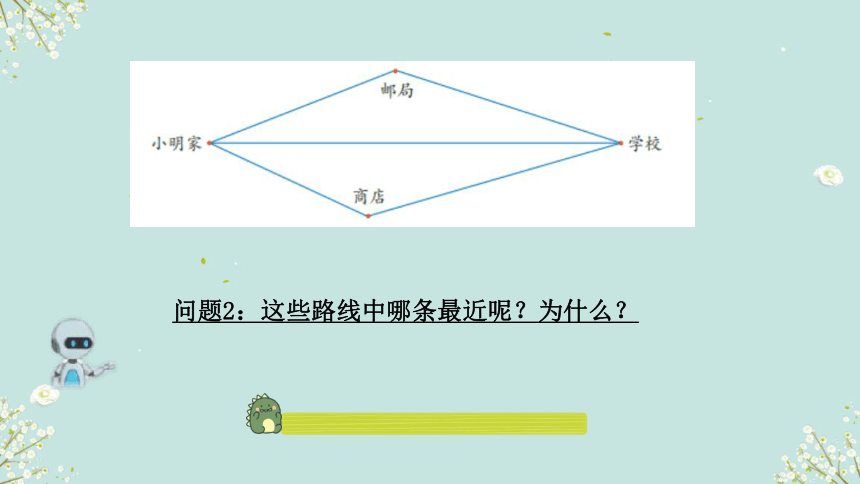
问题2:这些路线中哪条最近呢?为什么?
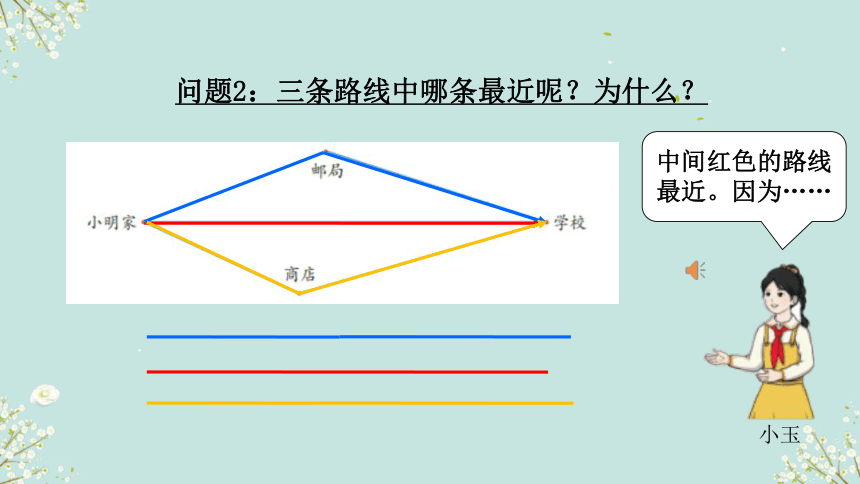
问题2:三条路线中哪条最近呢?为什么?
小玉
中间红色的路线最近。因为……
结
论
两点间所有连线中线段最短,这条线段的长度叫做两点间的距离。
“三角形的三边关系”
“最短路线问题”
?
你能从中找到我们学习过的平面图形吗?
问题1:只要有三条线段就一定可以围成三角形吗
“不一定”
小亮
小雪
乐乐
请拿出课前准备好的小棒,任选3根,试着围一围。
问题2:什么样的三条线段能围成三角形呢?
小光
小玉
我猜:
三角形两边的和大于第三边。
有以下4 组线段:
(1) 6cm、7cm、8cm;
(2) 3cm、6cm、10cm;
(3) 4cm、5cm、9cm;
(4) 8cm、11cm、11cm。
1.用直尺和圆规尝试作图验证以上4组线段能否围成三角形。
2.观察各组图中三条线段之间的长度关系,想一想,能够验证我们的猜想吗?
猜想:三角形两边的和大于第三边?
数学实验
(1) 6cm、7cm、8cm
能围成
小雪
1.画一条线段
2.画弧找交点
3.连点成线
8cm
8cm
8cm
(3) 4cm、5cm、9cm
(2) 3cm、6cm、10cm
(4) 8cm、11cm、11cm
能
围
成
(1) 6cm、7cm、8cm
不
能
围
成
猜想:三角形两边的和大于第三边?
(4) 8cm、11cm、11cm
(1) 6cm、7cm、8cm
8 cm + 11 cm > 11cm
8 cm + 11 cm > 11cm
11cm + 11 cm > 8 cm
6 cm + 7 cm > 8 cm
6 cm + 8 cm > 7 cm
8 cm + 7 cm > 6 cm
乐乐
三角形两边的和大于第三边?
(2) 3cm、6cm、10cm
三角形两边的和大于第三边?
小光
3 cm + 10 cm > 6 cm
6 cm + 10 cm > 3 cm
3 cm + 6 cm <10 cm
为什么 三角形呢?
不能围成
小玉
(3) 4cm、5cm、9cm
不能围成
4 cm + 9 cm > 5 cm
5 cm + 9 cm > 4 cm
三角形两边的和大于第三边?
4 cm + 5 cm = 9 cm
结
论
三角形 两边的和大于第三边。
任意
如何判断三条线段能否围成三角形呢?
6 cm + 7 cm > 8 cm
6 cm + 8 cm > 7 cm
8 cm + 7 cm > 6 cm
1.尺规作图
2.计算三条线段之间的长度关系
所有三角形任意两边的和都大于第三边吗?
三角形任意两边的和大于第三边。
所有三角形任意两边的和都大于第三边吗?
AC + BC > AB
C
A
B
1.下面哪组线段可以围成一个三角形?看谁做得又对又快!
(2) 4cm、6cm、10cm
(1) 12cm、5cm、9cm
(3) 8cm、3cm、3cm
5cm + 12cm > 9 cm
9cm + 12cm > 5 cm
4 cm + 6 cm = 10 cm
3 cm + 3 cm < 8 cm
小亮
能围成
小玉
两条短边的和等于最长边
两条短边的和小于最长边
不能围成
不能围成
两条短边的和大于最长边
不符合“三角形任意两边的和大于第三边”
三角形任意两边的和大于第三边
5cm + 9 cm > 12cm
如何判断三条线段能否围成三角形呢?
6 cm + 7 cm > 8 cm
1.尺规作图
2.计算三条线段之间的长度关系
2.计算两条较短线段之和与最长线段比较
6 cm + 8 cm > 7 cm
8 cm + 7 cm > 6 cm
2.三角形两条边的长分别为12cm和5cm,猜一猜,第三条边可能是多长?
7cm< 第三边
<17cm
12cm
5cm
9cm
12cm
5cm
?cm
12cm
5cm
?cm
12cm
3.三角形一条边的长是12cm,其余两条边的长度和是14cm,这两条边的长度分别可以是( )cm和( )cm。
A
AC + BC = 14
小光
小雪
12cm
8cm
6cm
7cm
7cm
9cm
椭
圆
5cm
B
C
三角形任意两边的和大于第三边。
结
论
两点间所有连线中线段最短,这条线段的长度叫做两点间的距离。
结
论
数学实验
探索结论
三角形的三边关系
生活经验
大胆猜想
由特殊向一般
推理验证
应用结论
解决问题
不懈
努力
正确
方法
+
=
成功
最具高度的三角形
数学书第64页,第6、7题。
思考题:
“姚明一步能走3米!”你相信吗?
姚明:
身高2.26米;
腿长1.31米。
三角形的三边关系(第三课时)
3.直尺、圆规、铅笔、橡皮
等文具。
1.学习任务单。
2.若干根长短不同的小棒。
问题1:小明从家到学校有几条路线?他可以怎样走?
问题1:小明从家到学校有几条路线?他可以怎样走?
小光
有三条。分别是……
问题2:这些路线中哪条最近呢?为什么?
问题2:三条路线中哪条最近呢?为什么?
小玉
中间红色的路线最近。因为……
结
论
两点间所有连线中线段最短,这条线段的长度叫做两点间的距离。
“三角形的三边关系”
“最短路线问题”
?
你能从中找到我们学习过的平面图形吗?
问题1:只要有三条线段就一定可以围成三角形吗
“不一定”
小亮
小雪
乐乐
请拿出课前准备好的小棒,任选3根,试着围一围。
问题2:什么样的三条线段能围成三角形呢?
小光
小玉
我猜:
三角形两边的和大于第三边。
有以下4 组线段:
(1) 6cm、7cm、8cm;
(2) 3cm、6cm、10cm;
(3) 4cm、5cm、9cm;
(4) 8cm、11cm、11cm。
1.用直尺和圆规尝试作图验证以上4组线段能否围成三角形。
2.观察各组图中三条线段之间的长度关系,想一想,能够验证我们的猜想吗?
猜想:三角形两边的和大于第三边?
数学实验
(1) 6cm、7cm、8cm
能围成
小雪
1.画一条线段
2.画弧找交点
3.连点成线
8cm
8cm
8cm
(3) 4cm、5cm、9cm
(2) 3cm、6cm、10cm
(4) 8cm、11cm、11cm
能
围
成
(1) 6cm、7cm、8cm
不
能
围
成
猜想:三角形两边的和大于第三边?
(4) 8cm、11cm、11cm
(1) 6cm、7cm、8cm
8 cm + 11 cm > 11cm
8 cm + 11 cm > 11cm
11cm + 11 cm > 8 cm
6 cm + 7 cm > 8 cm
6 cm + 8 cm > 7 cm
8 cm + 7 cm > 6 cm
乐乐
三角形两边的和大于第三边?
(2) 3cm、6cm、10cm
三角形两边的和大于第三边?
小光
3 cm + 10 cm > 6 cm
6 cm + 10 cm > 3 cm
3 cm + 6 cm <10 cm
为什么 三角形呢?
不能围成
小玉
(3) 4cm、5cm、9cm
不能围成
4 cm + 9 cm > 5 cm
5 cm + 9 cm > 4 cm
三角形两边的和大于第三边?
4 cm + 5 cm = 9 cm
结
论
三角形 两边的和大于第三边。
任意
如何判断三条线段能否围成三角形呢?
6 cm + 7 cm > 8 cm
6 cm + 8 cm > 7 cm
8 cm + 7 cm > 6 cm
1.尺规作图
2.计算三条线段之间的长度关系
所有三角形任意两边的和都大于第三边吗?
三角形任意两边的和大于第三边。
所有三角形任意两边的和都大于第三边吗?
AC + BC > AB
C
A
B
1.下面哪组线段可以围成一个三角形?看谁做得又对又快!
(2) 4cm、6cm、10cm
(1) 12cm、5cm、9cm
(3) 8cm、3cm、3cm
5cm + 12cm > 9 cm
9cm + 12cm > 5 cm
4 cm + 6 cm = 10 cm
3 cm + 3 cm < 8 cm
小亮
能围成
小玉
两条短边的和等于最长边
两条短边的和小于最长边
不能围成
不能围成
两条短边的和大于最长边
不符合“三角形任意两边的和大于第三边”
三角形任意两边的和大于第三边
5cm + 9 cm > 12cm
如何判断三条线段能否围成三角形呢?
6 cm + 7 cm > 8 cm
1.尺规作图
2.计算三条线段之间的长度关系
2.计算两条较短线段之和与最长线段比较
6 cm + 8 cm > 7 cm
8 cm + 7 cm > 6 cm
2.三角形两条边的长分别为12cm和5cm,猜一猜,第三条边可能是多长?
7cm< 第三边
<17cm
12cm
5cm
9cm
12cm
5cm
?cm
12cm
5cm
?cm
12cm
3.三角形一条边的长是12cm,其余两条边的长度和是14cm,这两条边的长度分别可以是( )cm和( )cm。
A
AC + BC = 14
小光
小雪
12cm
8cm
6cm
7cm
7cm
9cm
椭
圆
5cm
B
C
三角形任意两边的和大于第三边。
结
论
两点间所有连线中线段最短,这条线段的长度叫做两点间的距离。
结
论
数学实验
探索结论
三角形的三边关系
生活经验
大胆猜想
由特殊向一般
推理验证
应用结论
解决问题
不懈
努力
正确
方法
+
=
成功
最具高度的三角形
数学书第64页,第6、7题。
思考题:
“姚明一步能走3米!”你相信吗?
姚明:
身高2.26米;
腿长1.31米。
