第六章 统计——2023-2024学年高一数学北师大版(2019)必修一单元测试卷(含解析)
文档属性
| 名称 | 第六章 统计——2023-2024学年高一数学北师大版(2019)必修一单元测试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 721.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-09 19:58:06 | ||
图片预览




文档简介
第六章 统计——2023-2024学年高一数学北师大版(2019)必修一单元测试卷
一、单项选择题:本大题共 8 小题,每小题 5 分,共 40 分. 在每小题给出的四个选项中,只有一个选项是正确的.请把正确的选项填涂在答题卡相应的位置上.
1.某高中的三个年级共有学生2000人,其中高一600人,高二600人,高三800人,该校现在要了解学生对校本课程的看法,准备从全校学生中抽取80人进行访谈,若采取按比例分配的分层抽样,且按年级来分层,则高一年级应抽取的人数是( )
A.24 B.26 C.30 D.36
2.某学校有小学生270人,初中生x人,高中生810人.为了调查学校学生的近视率,采用分层抽样的方法从中抽取一个容量为360的样本,且从初中生中抽取的人数为120人,则x为( )
A.270 B.360 C.450 D.540
3.某企业为了解员工身体健康情况,采用分层抽样的方法从该企业的营销部门和研发部门抽取部分员工体检,已知该企业营销部门和研发部门的员工人数之比是,且被抽到参加体检的员工中,营销部门的人数比研发部门的人数多60,则参加体检的人数是( )
A.120 B.360 C.240 D.300
4.已知由小到大排列的5个样本数据a,12,16,19,23的极差是15,则a的值为( )
A.6 B.7 C.8 D.9
5.某电视台在因特网上就观众对其某一节目的喜爱程度进行调查,参加调查的一共有2000人,其中各种态度对应的人数如表所示:
最喜爱 喜爱 一般 不喜欢
480 720 640 160
电视台为了了解观众的具体想法和意见,打算从中抽选出100人进行更为详细的调查,为此要进行按比例分层抽样,那么在分层抽样时,每类人中应抽选出的人数分别为( )
A.24,36,32,8 B.48,72,64,16 C.20,40,30,10 D.25,25,25,25
6.已知某19个数据的平均数为5,方差为2,现加入一个数5,此时这20个数据的平均数为,方差为,则( )
A., B.,
C., D.,
7.有两位射击运动员在一次射击测试中各射靶10次,每次命中的环数如下:
甲:7,8,7,9,5,4,9,10,7,4
乙:9,5,7,8,7,6,8,6,7,7.
则下列结论正确的是( )
A.甲成绩的平均数较小 B.乙成绩的中位数较小
C.乙成绩的极差较大 D.乙比甲的成绩稳定
8.已知甲组数据由,,,这n个数据构成,记这组数据的平均数为,方差为;乙组数据由,,,,这数据构成,记这组数据的平均数为,方差为,则( )
A., B.,
C., D.,
二、多项选择题:本大题共 3 小题,每小题 6 分,共 18 分. 在每小题给出的四个选项中,有多项符合题目要求. 全部选对得 6 分,选对但不全的得部分分,有选错的得0分.
9.甲、乙两类水果的质量(单位:kg)分别服从正态分布、,其正态分布的密度曲线如图所示,则下列说法正确的是( )
A.甲类水果的平均质量
B.甲类水果的质量比乙类水果的质量更集中于平均值左右
C.甲类水果的平均质量比乙类水果的平均质量小
D.乙类水果的质量服从正态分布的参数
10.从某校随机抽取30名学生参加某项知识测试,得分(十分制)如图所示,则下列选项错误的是( )
A.这30名学生测试得分的中位数为6
B.这30名学生测试得分的众数与中位数相等
C.这30名学生测试得分的极差为8
D.这30名学生测试得分的平均数比中位数大
11.某农场种植的甲、乙两种水稻,在面积相等的两块稻田中连续5年的产量如下:
品种 第1年 第2年 第3年 第4年 第5年
甲/kg 560 580 570 590 600
乙/kg 550 600 580 580 590
若,分别表示甲、乙两种水稻产量的平均值,,分别表示甲、乙两种水稻产量的方差,则下列选项正确的是( )
A.
B.
C.甲种水稻产量的极差与乙种水稻产量的极差相等
D.乙种水稻的产量有三年位于之间
三、填空题:本大题共 3 小题,每小题 5 分,共 15 分.
12.某高中共有学生2000人,其中高一有400人,高二有800人,现采用按比例分配的分层抽样的方法抽取容量为25的样本,那么高二抽取的人数为________________.
13.某市场有四类食品,其中粮食类,蔬菜类,肉类和水果类分别有10种,20种,20种和50种,现在从中抽取一个容量为50的样本进行食品安全检测,若采用按比例分配的分层抽样的方法抽取样本,则抽取的粮食类和水果类的样本数之和为______.
14.一个射击运动员打靶6次的环数为:9,5,7,6,8,7,则这组数据的方差为____________.
注:一组数据,,…,的平均数为,它的方差为.
四、解答题:本题共 5 小题,共 77 分. 解答应写出文字说明、证明过程或演算步骤.
15.一支田径队共有运动员98人,其中女运动员有42人,用比例分配的分层随机抽样的方法抽取一个样本,每名运动员被抽到的概率都是,则男运动员应抽取多少人
16.某大学艺术专业400名学生参加某次测评,根据男、女学生人数比例使用分层随机抽样的方法从中随机抽取了100名学生,记录他们的分数,将数据分成7组:,,…,,并整理得到如图的频率分布直方图:
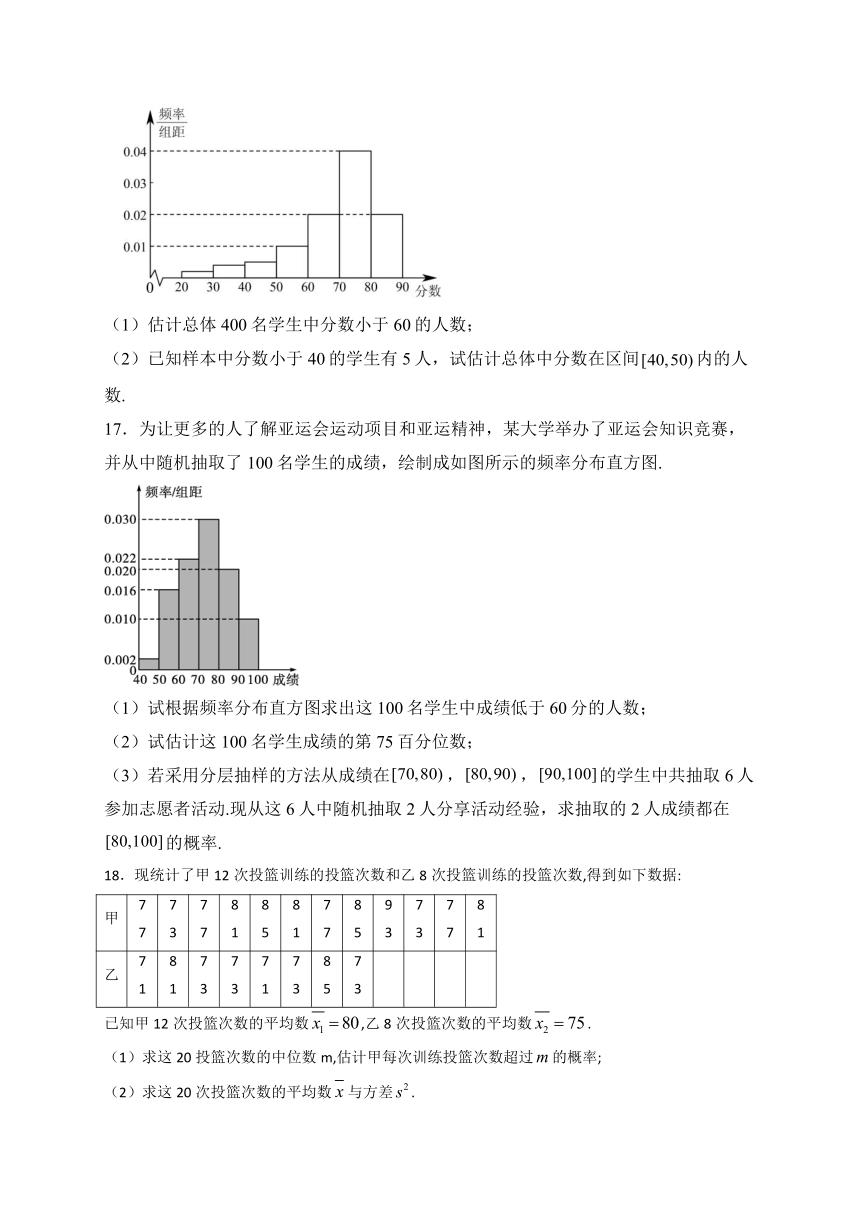
(1)估计总体400名学生中分数小于60的人数;
(2)已知样本中分数小于40的学生有5人,试估计总体中分数在区间内的人数.
17.为让更多的人了解亚运会运动项目和亚运精神,某大学举办了亚运会知识竞赛,并从中随机抽取了100名学生的成绩,绘制成如图所示的频率分布直方图.
(1)试根据频率分布直方图求出这100名学生中成绩低于60分的人数;
(2)试估计这100名学生成绩的第75百分位数;
(3)若采用分层抽样的方法从成绩在,,的学生中共抽取6人参加志愿者活动.现从这6人中随机抽取2人分享活动经验,求抽取的2人成绩都在的概率.
18.现统计了甲12次投篮训练的投篮次数和乙8次投篮训练的投篮次数,得到如下数据:
甲 77 73 77 81 85 81 77 85 93 73 77 81
乙 71 81 73 73 71 73 85 73
已知甲12次投篮次数的平均数,乙8次投篮次数的平均数.
(1)求这20投篮次数的中位数m,估计甲每次训练投篮次数超过的概率;
(2)求这20次投篮次数的平均数与方差.
19.某中学新建了学校食堂,每天有近2000名学生在学校食堂用午餐,午餐开放时间约40分钟,食堂制作了三类餐食,第一类是选餐,学生凭喜好在做好的大约6种菜和主食米饭中任意选购;第二类是套餐,已按配套好菜色盛装好,可直接取餐:第三类是面食,如煮面 炒粉等,为了更合理地设置口布局,增加学生的用餐满意度,学校学生会在用餐的学生中对就餐选择 各类餐食的平均每份取餐时长以及可接受等待时间进行问卷调查,并得到以下的统计图表:
类别 选餐 套餐 面食
选择人数 50 30 20
平均每份取餐时长(单位 分钟) 2 0.5 1
已知饭堂的售饭窗口一共有20个,就餐高峰期时有240名学生在等待就餐.
(1)根据以上调查统计,如果设置12个选餐窗口,4个套餐窗口,4个面食窗口,就餐高峰期时,假设大家在排队时自动选择较短的队伍等待(即各类餐食的窗口前队伍长度各自相同),求选择选餐的同学取到午餐的最长等待时间;
(2)取餐时至多等待多长时间能让的同学感到满意 (即在接受等待时长内取到餐,保留整数);
(3)根据以上的调查统计,从等待时长和公平的角度上考虑,如何设置各类售饭窗口数更优化,并给出你的求解过程.
参考答案
1.答案:A
解析:由题意,从全校2000人中抽取80人访谈,按照年级分层,则高一年级应该抽(人).
故选:A.
2.答案:D
解析:依题意初中生应抽取 120 人.
所以,解
故选:D.
3.答案:D
解析:设参加体检的员工中营销部门的人数为x,研发部门的人数为y,
因为采用分层抽样的方法,则①;
参加体检的员工中,营销部门的人数比研发部门的人数多60,则②,
联立①②解得,故参加体检的人数共.
故选:D.
4.答案:C
解析:由题知最小的数据是a,最大的数据是23,则极差为,解得.
故选:C.
5.答案:A
解析:最喜爱组应抽取人,喜爱组应抽取人,
一般组应抽取人,不喜欢组应抽取,
故选:A
6.答案:C
解析:原19个数据的平均数为5,方差为2,
加入一个数5之后,这20个数的
平均数为,
方差为.
故选:C.
7.答案:D
解析:将甲乙两位射击运动员的射击环数从小到大进行排列可得:
甲:4,4,5,7,7,7,8,9,9,10,
乙:5,6,6,7,7,7,7,8,8,9,
对于A:甲的射击环数的平均数,
乙的射击环数的平均数,所以甲乙成绩的平均数相等,故A错误;
对于B:甲的射击环数的中位数为,乙的射击环数的中位数为,所以甲乙成绩的中位数相等,故B错误;
对于C:易得甲的射击环数的极差为,乙的射击环数的极差为,所以甲成绩的极差较大,故C错误;
对于D:因为甲的射击环数的平均数,
所以甲的射击环数的方差为:
,
因为乙的射击环数的平均数,
所以乙的射击环数的方差为:
,
所以,所以乙比甲的成绩稳定,故D正确.
故选:D
8.答案:D
解析:由已知可得,
,
,
,
所以ABC错误,D正确.
故选:D.
9.答案:ABC
解析:由图象可知甲的正态曲线关于直线对称,乙的正态曲线关于直线对称,所以,,故A正确,C正确.
由图可知甲类水果的质量分布比乙类水果的质量分布更集中于平均值左右,故B正确.
因为乙的正态曲线的峰值为1.99,即,所以,故D错误.
故选ABC
10.答案:ABC
解析:这30名学生测试得分的中位数为,故A错误;
这30名学生测试得分的众数为5,故B错误;
分数最高为10,最低为3,所以极差为7,故C错误;
这30名学生测试得分的平均数为:
,故D正确.
故选:ABC.
11.答案:ABD
解析:A.,,所以,故A正确;
B.,
,
所以,故B正确;
C.甲种水稻产量的极差为:,乙种水稻产量的极差为:,甲种水稻产量的极差小于乙种水稻产量的极差,故C错误;
D.,所以为,因为,所以,,所以乙种水稻的产量有三年位于之间,故D正确.
故选:ABD
12.答案:10
解析:由题意,高二人数占总人数的比例为,
所以高二抽取的人数为.
故答案为:10.
13.答案:30
解析:设抽取的粮食类和水果类的样本数之和为x,由题意,得,解得.
14.答案:
解析:因为,
所以
.
故答案为:.
15.答案:(人)
解析:田径队共有运动员98人,其中女运动员有42人,男运动员有56人,每名运动员被抽到的概率都是,男运动员应抽取(人)。
16.答案:(1)80;
(2)20
解析:(1)根据频率分布直方图可知,样本中分数不小于60的频率为,
所以样本中分数小于60的频率为,
所以估计总体400名学生中分数小于60的人数为.
(2)根据题意,样本中分数不小于50的频率为,
样本中分数在区间内的人数为,
所以总体中分数在区间内的人数估计为.
17.答案:(1)18;(2)82.5;(3)
解析:(1)由频率分布直方图中数据可知(人);
(2)成绩小于或等于80的频率为,
成绩在的频率为,因为,
所以这100名学生成绩的第75百分位数在内,
所以随机抽取的100名学生成绩的第75百分位数为.
(3)因为成绩在,,的学生人数所占比例为,所以从成绩在,,所抽取人数分别为3,2,1.
记抽取成绩在内的3人为a,b,c,成绩在上的3人为D,E,F.
从这6人中随机抽取2人的所有可能为,,,,,,,,,,,,,,,共15种,
抽取的2人成绩都在的是,,,共3种,抽取的2人成绩都在的概率为.
18.答案:(1)
(2)33
解析:(1)将这20个数据从小到大排列,第10个数和第11个数都是77,所以
估计甲每次训练投篮次数超过m的概率为.
(2)这20次投篮次数的平均数,方差.
19.答案:(1)20分钟;
(2)18分钟;
(3)答案见解析
解析:(1)由题意得就餐高峰期时选择选餐的总人数为人;这120人平均分布在12个选餐窗口,平均每个窗口等待就餐的人数为人,所以选择选餐的同学取到午餐的最长等待时间为分钟,
(2)由可接受等待时长的频率分布直方图可知,
分组为,,,的频率分别为0.15,0.45,0.35,0.05,
所以可接受等待时长在分钟以内的同学占0.05,即有95%的同学不满意
可接受等待时长在分钟以内的同学占,
即有的同学对等待时间少于15分钟感到满意,
所以至多等待的时间,能让80%的同学感到满意
,所以分钟,
至多等待18分钟,能让80%的同学感到满意.
(3)假设设置m个选餐窗口,n个套餐窗口,k个面食窗口,
则各队伍的同学最长等待时间如下:
类别 选餐 套餐 面食
高峰期就餐总人数 120 72 48
各队伍长度(人)
最长等待时间(分钟)
依题意,从等待时长和公平的角度上考虑,则要求每个队伍的最长等待时间大致相同,即得,即有,
而,故,,,
因此建议设置选餐 套餐 面食三个类别的窗口数分别为15,2,3个.
一、单项选择题:本大题共 8 小题,每小题 5 分,共 40 分. 在每小题给出的四个选项中,只有一个选项是正确的.请把正确的选项填涂在答题卡相应的位置上.
1.某高中的三个年级共有学生2000人,其中高一600人,高二600人,高三800人,该校现在要了解学生对校本课程的看法,准备从全校学生中抽取80人进行访谈,若采取按比例分配的分层抽样,且按年级来分层,则高一年级应抽取的人数是( )
A.24 B.26 C.30 D.36
2.某学校有小学生270人,初中生x人,高中生810人.为了调查学校学生的近视率,采用分层抽样的方法从中抽取一个容量为360的样本,且从初中生中抽取的人数为120人,则x为( )
A.270 B.360 C.450 D.540
3.某企业为了解员工身体健康情况,采用分层抽样的方法从该企业的营销部门和研发部门抽取部分员工体检,已知该企业营销部门和研发部门的员工人数之比是,且被抽到参加体检的员工中,营销部门的人数比研发部门的人数多60,则参加体检的人数是( )
A.120 B.360 C.240 D.300
4.已知由小到大排列的5个样本数据a,12,16,19,23的极差是15,则a的值为( )
A.6 B.7 C.8 D.9
5.某电视台在因特网上就观众对其某一节目的喜爱程度进行调查,参加调查的一共有2000人,其中各种态度对应的人数如表所示:
最喜爱 喜爱 一般 不喜欢
480 720 640 160
电视台为了了解观众的具体想法和意见,打算从中抽选出100人进行更为详细的调查,为此要进行按比例分层抽样,那么在分层抽样时,每类人中应抽选出的人数分别为( )
A.24,36,32,8 B.48,72,64,16 C.20,40,30,10 D.25,25,25,25
6.已知某19个数据的平均数为5,方差为2,现加入一个数5,此时这20个数据的平均数为,方差为,则( )
A., B.,
C., D.,
7.有两位射击运动员在一次射击测试中各射靶10次,每次命中的环数如下:
甲:7,8,7,9,5,4,9,10,7,4
乙:9,5,7,8,7,6,8,6,7,7.
则下列结论正确的是( )
A.甲成绩的平均数较小 B.乙成绩的中位数较小
C.乙成绩的极差较大 D.乙比甲的成绩稳定
8.已知甲组数据由,,,这n个数据构成,记这组数据的平均数为,方差为;乙组数据由,,,,这数据构成,记这组数据的平均数为,方差为,则( )
A., B.,
C., D.,
二、多项选择题:本大题共 3 小题,每小题 6 分,共 18 分. 在每小题给出的四个选项中,有多项符合题目要求. 全部选对得 6 分,选对但不全的得部分分,有选错的得0分.
9.甲、乙两类水果的质量(单位:kg)分别服从正态分布、,其正态分布的密度曲线如图所示,则下列说法正确的是( )
A.甲类水果的平均质量
B.甲类水果的质量比乙类水果的质量更集中于平均值左右
C.甲类水果的平均质量比乙类水果的平均质量小
D.乙类水果的质量服从正态分布的参数
10.从某校随机抽取30名学生参加某项知识测试,得分(十分制)如图所示,则下列选项错误的是( )
A.这30名学生测试得分的中位数为6
B.这30名学生测试得分的众数与中位数相等
C.这30名学生测试得分的极差为8
D.这30名学生测试得分的平均数比中位数大
11.某农场种植的甲、乙两种水稻,在面积相等的两块稻田中连续5年的产量如下:
品种 第1年 第2年 第3年 第4年 第5年
甲/kg 560 580 570 590 600
乙/kg 550 600 580 580 590
若,分别表示甲、乙两种水稻产量的平均值,,分别表示甲、乙两种水稻产量的方差,则下列选项正确的是( )
A.
B.
C.甲种水稻产量的极差与乙种水稻产量的极差相等
D.乙种水稻的产量有三年位于之间
三、填空题:本大题共 3 小题,每小题 5 分,共 15 分.
12.某高中共有学生2000人,其中高一有400人,高二有800人,现采用按比例分配的分层抽样的方法抽取容量为25的样本,那么高二抽取的人数为________________.
13.某市场有四类食品,其中粮食类,蔬菜类,肉类和水果类分别有10种,20种,20种和50种,现在从中抽取一个容量为50的样本进行食品安全检测,若采用按比例分配的分层抽样的方法抽取样本,则抽取的粮食类和水果类的样本数之和为______.
14.一个射击运动员打靶6次的环数为:9,5,7,6,8,7,则这组数据的方差为____________.
注:一组数据,,…,的平均数为,它的方差为.
四、解答题:本题共 5 小题,共 77 分. 解答应写出文字说明、证明过程或演算步骤.
15.一支田径队共有运动员98人,其中女运动员有42人,用比例分配的分层随机抽样的方法抽取一个样本,每名运动员被抽到的概率都是,则男运动员应抽取多少人
16.某大学艺术专业400名学生参加某次测评,根据男、女学生人数比例使用分层随机抽样的方法从中随机抽取了100名学生,记录他们的分数,将数据分成7组:,,…,,并整理得到如图的频率分布直方图:
(1)估计总体400名学生中分数小于60的人数;
(2)已知样本中分数小于40的学生有5人,试估计总体中分数在区间内的人数.
17.为让更多的人了解亚运会运动项目和亚运精神,某大学举办了亚运会知识竞赛,并从中随机抽取了100名学生的成绩,绘制成如图所示的频率分布直方图.
(1)试根据频率分布直方图求出这100名学生中成绩低于60分的人数;
(2)试估计这100名学生成绩的第75百分位数;
(3)若采用分层抽样的方法从成绩在,,的学生中共抽取6人参加志愿者活动.现从这6人中随机抽取2人分享活动经验,求抽取的2人成绩都在的概率.
18.现统计了甲12次投篮训练的投篮次数和乙8次投篮训练的投篮次数,得到如下数据:
甲 77 73 77 81 85 81 77 85 93 73 77 81
乙 71 81 73 73 71 73 85 73
已知甲12次投篮次数的平均数,乙8次投篮次数的平均数.
(1)求这20投篮次数的中位数m,估计甲每次训练投篮次数超过的概率;
(2)求这20次投篮次数的平均数与方差.
19.某中学新建了学校食堂,每天有近2000名学生在学校食堂用午餐,午餐开放时间约40分钟,食堂制作了三类餐食,第一类是选餐,学生凭喜好在做好的大约6种菜和主食米饭中任意选购;第二类是套餐,已按配套好菜色盛装好,可直接取餐:第三类是面食,如煮面 炒粉等,为了更合理地设置口布局,增加学生的用餐满意度,学校学生会在用餐的学生中对就餐选择 各类餐食的平均每份取餐时长以及可接受等待时间进行问卷调查,并得到以下的统计图表:
类别 选餐 套餐 面食
选择人数 50 30 20
平均每份取餐时长(单位 分钟) 2 0.5 1
已知饭堂的售饭窗口一共有20个,就餐高峰期时有240名学生在等待就餐.
(1)根据以上调查统计,如果设置12个选餐窗口,4个套餐窗口,4个面食窗口,就餐高峰期时,假设大家在排队时自动选择较短的队伍等待(即各类餐食的窗口前队伍长度各自相同),求选择选餐的同学取到午餐的最长等待时间;
(2)取餐时至多等待多长时间能让的同学感到满意 (即在接受等待时长内取到餐,保留整数);
(3)根据以上的调查统计,从等待时长和公平的角度上考虑,如何设置各类售饭窗口数更优化,并给出你的求解过程.
参考答案
1.答案:A
解析:由题意,从全校2000人中抽取80人访谈,按照年级分层,则高一年级应该抽(人).
故选:A.
2.答案:D
解析:依题意初中生应抽取 120 人.
所以,解
故选:D.
3.答案:D
解析:设参加体检的员工中营销部门的人数为x,研发部门的人数为y,
因为采用分层抽样的方法,则①;
参加体检的员工中,营销部门的人数比研发部门的人数多60,则②,
联立①②解得,故参加体检的人数共.
故选:D.
4.答案:C
解析:由题知最小的数据是a,最大的数据是23,则极差为,解得.
故选:C.
5.答案:A
解析:最喜爱组应抽取人,喜爱组应抽取人,
一般组应抽取人,不喜欢组应抽取,
故选:A
6.答案:C
解析:原19个数据的平均数为5,方差为2,
加入一个数5之后,这20个数的
平均数为,
方差为.
故选:C.
7.答案:D
解析:将甲乙两位射击运动员的射击环数从小到大进行排列可得:
甲:4,4,5,7,7,7,8,9,9,10,
乙:5,6,6,7,7,7,7,8,8,9,
对于A:甲的射击环数的平均数,
乙的射击环数的平均数,所以甲乙成绩的平均数相等,故A错误;
对于B:甲的射击环数的中位数为,乙的射击环数的中位数为,所以甲乙成绩的中位数相等,故B错误;
对于C:易得甲的射击环数的极差为,乙的射击环数的极差为,所以甲成绩的极差较大,故C错误;
对于D:因为甲的射击环数的平均数,
所以甲的射击环数的方差为:
,
因为乙的射击环数的平均数,
所以乙的射击环数的方差为:
,
所以,所以乙比甲的成绩稳定,故D正确.
故选:D
8.答案:D
解析:由已知可得,
,
,
,
所以ABC错误,D正确.
故选:D.
9.答案:ABC
解析:由图象可知甲的正态曲线关于直线对称,乙的正态曲线关于直线对称,所以,,故A正确,C正确.
由图可知甲类水果的质量分布比乙类水果的质量分布更集中于平均值左右,故B正确.
因为乙的正态曲线的峰值为1.99,即,所以,故D错误.
故选ABC
10.答案:ABC
解析:这30名学生测试得分的中位数为,故A错误;
这30名学生测试得分的众数为5,故B错误;
分数最高为10,最低为3,所以极差为7,故C错误;
这30名学生测试得分的平均数为:
,故D正确.
故选:ABC.
11.答案:ABD
解析:A.,,所以,故A正确;
B.,
,
所以,故B正确;
C.甲种水稻产量的极差为:,乙种水稻产量的极差为:,甲种水稻产量的极差小于乙种水稻产量的极差,故C错误;
D.,所以为,因为,所以,,所以乙种水稻的产量有三年位于之间,故D正确.
故选:ABD
12.答案:10
解析:由题意,高二人数占总人数的比例为,
所以高二抽取的人数为.
故答案为:10.
13.答案:30
解析:设抽取的粮食类和水果类的样本数之和为x,由题意,得,解得.
14.答案:
解析:因为,
所以
.
故答案为:.
15.答案:(人)
解析:田径队共有运动员98人,其中女运动员有42人,男运动员有56人,每名运动员被抽到的概率都是,男运动员应抽取(人)。
16.答案:(1)80;
(2)20
解析:(1)根据频率分布直方图可知,样本中分数不小于60的频率为,
所以样本中分数小于60的频率为,
所以估计总体400名学生中分数小于60的人数为.
(2)根据题意,样本中分数不小于50的频率为,
样本中分数在区间内的人数为,
所以总体中分数在区间内的人数估计为.
17.答案:(1)18;(2)82.5;(3)
解析:(1)由频率分布直方图中数据可知(人);
(2)成绩小于或等于80的频率为,
成绩在的频率为,因为,
所以这100名学生成绩的第75百分位数在内,
所以随机抽取的100名学生成绩的第75百分位数为.
(3)因为成绩在,,的学生人数所占比例为,所以从成绩在,,所抽取人数分别为3,2,1.
记抽取成绩在内的3人为a,b,c,成绩在上的3人为D,E,F.
从这6人中随机抽取2人的所有可能为,,,,,,,,,,,,,,,共15种,
抽取的2人成绩都在的是,,,共3种,抽取的2人成绩都在的概率为.
18.答案:(1)
(2)33
解析:(1)将这20个数据从小到大排列,第10个数和第11个数都是77,所以
估计甲每次训练投篮次数超过m的概率为.
(2)这20次投篮次数的平均数,方差.
19.答案:(1)20分钟;
(2)18分钟;
(3)答案见解析
解析:(1)由题意得就餐高峰期时选择选餐的总人数为人;这120人平均分布在12个选餐窗口,平均每个窗口等待就餐的人数为人,所以选择选餐的同学取到午餐的最长等待时间为分钟,
(2)由可接受等待时长的频率分布直方图可知,
分组为,,,的频率分别为0.15,0.45,0.35,0.05,
所以可接受等待时长在分钟以内的同学占0.05,即有95%的同学不满意
可接受等待时长在分钟以内的同学占,
即有的同学对等待时间少于15分钟感到满意,
所以至多等待的时间,能让80%的同学感到满意
,所以分钟,
至多等待18分钟,能让80%的同学感到满意.
(3)假设设置m个选餐窗口,n个套餐窗口,k个面食窗口,
则各队伍的同学最长等待时间如下:
类别 选餐 套餐 面食
高峰期就餐总人数 120 72 48
各队伍长度(人)
最长等待时间(分钟)
依题意,从等待时长和公平的角度上考虑,则要求每个队伍的最长等待时间大致相同,即得,即有,
而,故,,,
因此建议设置选餐 套餐 面食三个类别的窗口数分别为15,2,3个.
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
