2023-2024学年人教A版必修第二册 第八章 立体几何初步 单元测试(含解析)
文档属性
| 名称 | 2023-2024学年人教A版必修第二册 第八章 立体几何初步 单元测试(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-09 19:59:24 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2023-2024学年人教A版必修第二册 第八章 立体几何初步 单元测试
一、选择题
1.已知a,b是两条不同的直线,是平面,且,,则“”是“”的( )
A.充分不必要条件 B.必要不充分条件
C.既不充分又不必要条件 D.充要条件
2.设m,n是不同的直线,,是不同的平面,则下列命题正确的是( )
A.若,,,则 B.若,,,则
C.若,,,则 D.若,,,则
3.在正方体中,点O为线段BD的中点,设点P在直线上,直线OP与平面所成的角为,则的取值范围是( )
A. B. C. D.
4.在四面体ABCD中,为正三角形,AB与平面BCD不垂直,则下列说法正确的是( )
A.AB与CD可能垂直
B.A在平面BCD内的射影可能是B
C.AB与CD不可能垂直
D.平面ABC与平面BCD不可能垂直
5.已知矩形,,.将沿矩形的对角线BD所在的直线进行翻折,在翻折过程中( )
A.存在某个位置,使得直线AC与BD垂直
B.存在某个位置,使得直线AB与CD垂直
C.存在某个位置,使得直线AD与BC垂直
D.对任意位置,三对直线“AC与BD”“AB与CD”“AD与BC”均不垂直
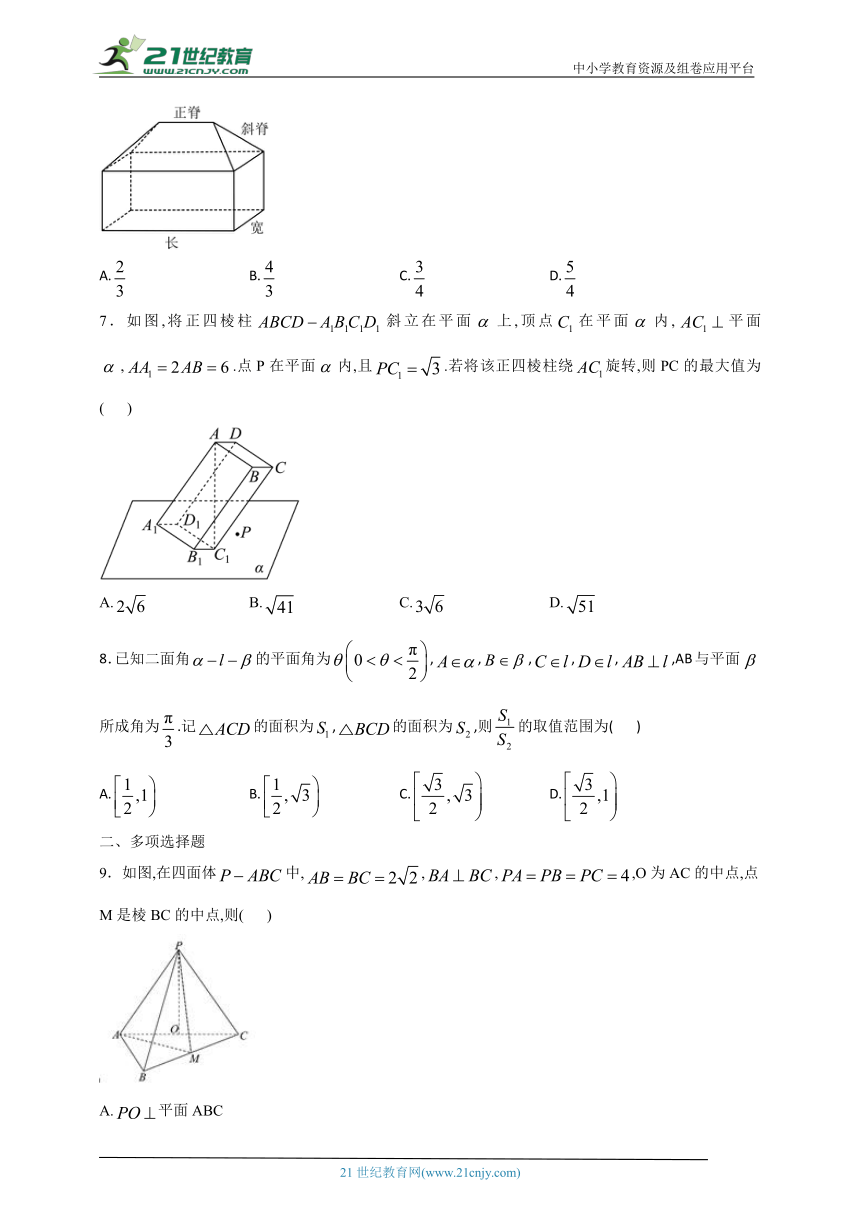
6.成语“运筹帷幄之中,决胜千里之外”,意思是在小小的军帐之内作出正确的部署,决定了千里之外战场上的胜利,说的是运筹的重要性.“帷幄”是古代打仗必备的帐篷,又称“幄帐”,如图是一种幄帐示意图,帐顶采用“五脊四坡式”,四条斜脊的长度相等,一条正脊平行于底面.若各斜坡面与底面所成二面角的正切值均为,底面矩形的长与宽之比为,则正脊与斜脊长度的比值为( )
A. B. C. D.
7.如图,将正四棱柱斜立在平面上,顶点在平面内,平面,.点P在平面内,且.若将该正四棱柱绕旋转,则PC的最大值为( )
A. B. C. D.
8.已知二面角的平面角为,,,,,,AB与平面所成角为.记的面积为,的面积为,则的取值范围为( )
A. B. C. D.
二、多项选择题
9.如图,在四面体中,,,,O为AC的中点,点M是棱BC的中点,则( )
A.平面ABC
B.
C.四面体的体积为
D.异面直线PM与AB所成角的余弦值为
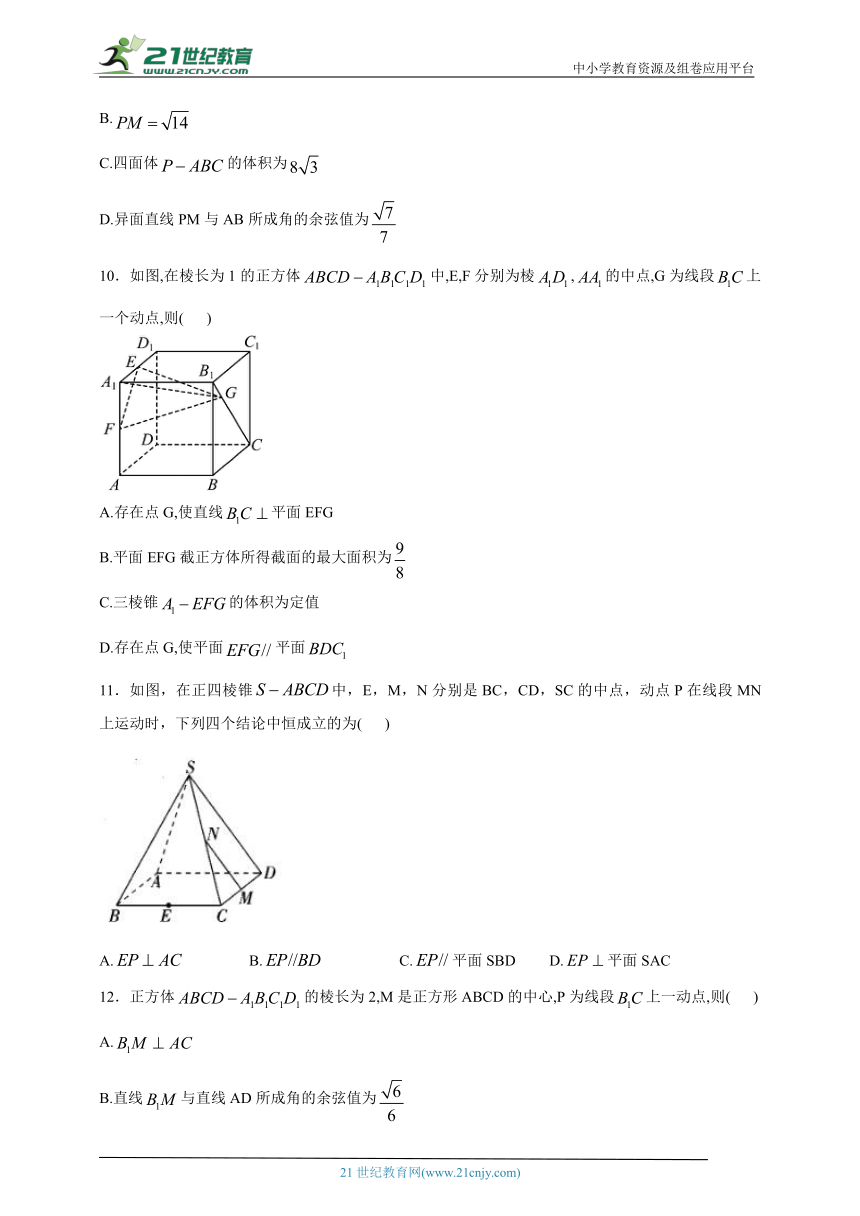
10.如图,在棱长为1的正方体中,E,F分别为棱,的中点,G为线段上一个动点,则( )
A.存在点G,使直线平面EFG
B.平面EFG截正方体所得截面的最大面积为
C.三棱锥的体积为定值
D.存在点G,使平面平面
11.如图,在正四棱锥中,E,M,N分别是BC,CD,SC的中点,动点P在线段MN上运动时,下列四个结论中恒成立的为( )
A. B. C.平面SBD D.平面SAC
12.正方体的棱长为2,M是正方形ABCD的中心,P为线段上一动点,则( )
A.
B.直线与直线AD所成角的余弦值为
C.不存在点P使得平面
D.三棱锥的体积为定值
三、填空题
13.已知三个互不重合的平面,,,且直线m,n不重合,由下列条件:①,;②,;③,,;能推得的条件是__________.
14.如图,在正方体中,点P在线段上运动,有下列判断:①平面平面;②平面;③异面直线与所成角的取值范围是;④三棱锥的体积不变.其中,正确的是__________(把所有正确判断的序号都填上).
15.刻画空间弯曲性是几何研究的重要内容,用“曲率”刻画空间弯曲性,规定:多面体顶点的曲率等于与多面体在该点的面角之和的差(多面体的面的内角叫做多面体的面角,角度用弧度制).例如,正四面体的每个顶点有个面角,每个面角为,所以正四面体在各顶点的曲率为.在底面为矩形的四棱锥中,底面ABCD,,PC与底面ABCD所成的角为,在四棱锥中,顶点的曲率为______.
16.在四棱锥中,底面ABCD是边长为的正方形,P在底面的射影为正方形的中心O,,Q点为AO中点.点T为该四棱锥表面上一个动点,满足PA、BD都平行于过QT的四棱锥的截面,则动点T的轨迹围成的多边形的面积为__________________.
四、解答题
17.如图,在四棱锥中,底面ABCD是矩形,PA为点P到平面ABCD的距离,,,,点E,M分别在线段AB,PC上,其中E是AB中点,,连接ME.
(1)当时,证明:直线平面PAD;
(2)当时,求三棱锥的体积.
18.如图1,在直角梯形ABCD中,,,,将沿AC折起(如图2).在图2所示的几何体中:
(1)若平面平面ABC,求证:;
(2)设P为BD的中点,记P到平面ACD的距离为,P到平面ABC的距离为,求证:为定值,并求出此定值.
19.在正方体中,M,N分别是线段,BD的中点.
(1)求证:平面;
(2)若正方体的棱长为2,求三棱锥的体积.
20.如图,在四棱锥中,底面ABCD是正方形,侧棱底面,.
(1)证明:平面平面PBD;
(2)点H在棱PC上,当二面角的余弦值为时,求.
参考答案
1.答案:B
解析:当,,时,直线a与直线b的位置关系是平行或者异面,故充分性不成立;当,,时,由直线与平面平行的判定定理,知,故必要性成立,所以“”是“”的必要不充分条件.
2.答案:D
解析:对于A,若,,,则直线m与n可能相交,也可能平行,还可能是异面直线,A错误;
对于B,若,则,B错误;
对于C,若,直线m与n可能平行,
如直线m,n都平行于,的交线,且,,满足条件,而,C错误;
对于D,若,,则,又,因此,D正确.
故选:D
3.答案:A
解析:由题意可得:直线OP于平面所成的角的取值范围:
不妨取 .
在中, .
的取值范围是 .
故答案为.
4.答案:A
解析:如图所示:取CD的中点E,连接AE,BE
假设,因为为等边三角形,所以,
又因为,所以平面ABE,所以
又因为E是CD中点,所以,只需满足,即可做到,故A正确C错误;
对于B:若A在平面BCD内的射影为B,则有平面BCD,与题干矛盾,故B错误;
对于D:过C点可以做出一条直线,使得该直线垂直与平面BCD,A点只需在该直线上,
即满足平面BCD即可达到要求,故D错误.
故选:A.
5.答案:C
解析:如图,作于点E,于点F.
因为,,所以,.
A项,若存在某个位置;使得直线AC与直线BD垂直,因为,连接,平面AEC,所以平面AEC,从而,这与已知矛盾,排除A;B项,若存在某个位置,使得直线AB与直线CD垂直,因为,平面ABC,所以平面ABC,因为平面BCD,所以平面平面BCD,取BC中点M,连接ME(图略),则,所以就是二面角的平面角,此角显然存在,即当A在底面BCD上的射影位于BC的中点时,直线AB与直线CD垂直,故B正确;C项,若存在某个位置,使得直线AD与直线BC垂直,因为,所以平面ACD,从而平面平面BCD,即A在底面BCD上的射影应位于线段CD上,这是不可能的,故排除C;D项,由以上所述,可排除D.故选B.
6.答案:B
解析:如图,多面体中,取AB的中点C,做交MN于Q,
做底面ABNM于E点,则E点在CQ上,且E点到BN,AM的距离相等,即,做于H点,连接EH,,则平面DHE,
所以,所以坡面与底面所成二面角为,又,则平面DCE,
所以,坡面与底面所成二面角为,
所以正切值,
不妨设,,
可得斜脊,因为矩形宽,
所以长为8,这样正脊,所以正脊与斜脊长度的比值为即.
故选:B.
7.答案:D
解析:过点C作,垂足为E,连接AC,可知平面,
所以点C到平面的距离为,
由题意,
,,
过点C作平面,垂足为,
因为点P在平面内,且,即点P在以为圆心,为半径的圆上,
当,,P三点共线时,且时,PC取最大值,
最大值为.
故选:D.
8.答案:C
解析:作,垂足为E,连接BE,
因为,即,,AE,平面AEB,
故平面AEB,平面AEB,故,
又,故平面,平面,
则AB在内的射影在BE上,则为AB与平面所成角,即,
由于,,故为二面角的平面角,即,
,
在中,,
则,
而,则,
则,,
故,
故选:C
9.答案:ABD
解析:对A:连结OB,
如图,在四面体中,,,,O为AC的中点,
所以,,且,.
所以,所以.
又因为,OB,平面ABC,所以平面ABC,故A正确;
对B、C、D:连接OM,由A知,平面ABC,平面ABC,所以,,
所以,故B正确;
因为AB与OM平行,所以OM与PM所成的角就是PM与AB所成角,在直角三角形POM中,,故D正确;
四面体的体积:,故C错误;
故选:ABD.
10.答案:AC
解析:对于A项,如图所示,
取中点H,I,连接HI交于G点,此时,
由正方体的性质知:面,又,则面,
面,可得,
在正方形中,易知,,面EFG,
所以平面EFG,故A正确;
对于B项,若G点靠C远,如图一示,过G作,即截面为四边形EFQR,
显然该截面在G为侧面CB1的中心时取得最大,最大值为,
若G靠C近时,如图二示,G作KJEF,延长EF交,DA延长线于M,H,
连接MK,HJ交,AB于L,I,则截面为六边形EFIJKL,
若K,J为中点时六边形面积为,,即B错误;
对于C项,随着G移动但G到面的距离始终不变即,
故是定值,即C正确;
对于D项,如图所示,连接,H为侧面的中心,则面与面和面分别交于线PG,DH,
若存在G点使平面平面,则,又,
则四边形PGHD为平行四边形,即,而,
此时G应在延长线上,故D错误;
故选:AC
11.答案:AC
解析:如图所示,连接AC,BD相交于点O,连接EM,EN,SO.由正四棱锥,可得底面,,所以.因为,所以平面SBD.
因为E,M,N分别是BC,CD,SC的中点,所以,,而,所以平面平面SBD,所以平面EMN,所以,故A正确;
由异面直线的定义可知,当P与M不重合时,EP与BD是异面直线,不可能有,因此B不正确;
平面平面SBD,所以平面SBD,因此C正确;平面SAC,若平面SAC,则,与相矛盾,因此当P与M不重合时,EP与平面SAC不垂直,即D不正确.故选AC.
12.答案:ABD
解析:对于选项A:在中,是的中点,故,正确;
对于选项B:设N是AB的中点,连接MN,则,
所以是异面直线与直线所成角(或其补角),
在中,,,,
所以,正确;
对于选项C:根据正方体的性质可知,,
由于平面,平面,所以平面,
同理可证得平面,
由于,BD,平面,所以平面平面,
当时,平面,所以平面,
即存在点P使得平面,错误;
对于选项D:,正确.
故选:ABD.
13.答案:②
解析:对于①,可能,所以①不成立;对于②,根据面面平行的性质可知,条件②能推出.对于③,可能,所以③不成立.所以能推得的条件是②.
故答案:②.
14.答案:①②④
解析:对于①,在正方体中,平面,平面,
平面平面,故①正确;
对于②,连接,如图:
容易证明平面//平面,
又平面,
平面故②正确;
对于③,,
异面直线与所成的角就是直线AP与所成的角,
在中,易知所求角的范围是,故③错误;
对于④,
点C到平面的距离不变,且的面积不变,
三棱锥的体积不变,故④正确.
综上所述,正确的是①②④.
故答案为:①②④.
15.答案:或
解析:
设,则,
平面ABCD,即为与底面ABCD所成角,即,
,,
,,;
平面ABCD,平面ABCD,,
又,,PA,平面PAB,平面PAB,
平面PAB,,即,又,
顶点的曲率为.
故答案为:.
16.答案:
解析:取AD的中点E,PD的中点F,PO的中点R,PB的中点N,
连接QR延长交PC与点M,依次连接E,F,M,N,G,
可知,,,即,而,
所以E,F,G,Q,N,R共面,所以E,F,M,N,G共面,
因为底面ABCD是边长为的正方形,
所以对角线,,
因为P在底面的射影为正方形的中心,可得面ABCD,
因为面ABCD,所以,
因为,,所以,
因为E、F分别为AD、PD的中点,
所以,且,
因为平面EFMG,平面EFMG,
所以平面EFMG,同理平面EFMG,
所以平面EFMG即为所求截面.
又因为平面平面,平面APC,所以,
因为Q为AO的中点,可得,
所以, ,,
因为N、F分别为PB、PD的中点,所以,,
所以,,所以四边形EFNG是平行四边形,
因为,,,所以平面APC,
因为平面APC,可得,所以,
所以四边形EFNG是矩形,
所以动点T的轨迹围成的多边形的面积为.
故答案为:.
17.答案:(1)证明见解析
(2)2
解析:(1)取PD中点N,连接MN,AN,
是的中位线,MN//CD,且,
又AE//CD,且,四边形AEMN为平行四边形,
又平面PAD,平面PAD,平面PAD.
(2),P到平面ABCD距离为3,
点M到平面ABCD的距离为1,
.
18.答案:(1)证明见解析
(2)证明见解析,2
解析:(1)记,在中,,,
在中,,由余弦定理得,
所以,所以,
因为平面平面ABC,平面平面,BC平面ABC,
所以平面ACD,又平面ACD,所以;
(2)由题意,,
因为P为BD的中点,,
所以,即.
19.答案:(1)证明见解析
(2)
解析:(1)连接,AN,如下图:
是线段BD的中点,底面ABCD是长方形,是线段AC的中点,
又是线段的中点,在中,,
平面,平面,平面.
(2)取BC的中点为O,连接MO,如下图:
,O分别是线段,BC的中点,在中,,,
又在正方体中,平面ABCD,平面ABCD,
为BD的中点,,
.
20.答案:(1)证明见解析
(2)
解析:(1)证明:如图,连接,侧棱底面,平面ABCD,.
又底面ABCD是正方形,.而且,,平面PBD,平面PBD.又平面,平面平面PBD.
(2)如图,过H作交DC于点E,过E作于点F,连接HF.
在平面PDC中,,,,底面ABCD,平面ABCD.
又平面,.
又,,,平面HEF,
平面HEF.又平面,,为二面角的平面角.故,则.
设,则,,.
在中,,.
在中,,
,当二面角的余弦值为时,.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
2023-2024学年人教A版必修第二册 第八章 立体几何初步 单元测试
一、选择题
1.已知a,b是两条不同的直线,是平面,且,,则“”是“”的( )
A.充分不必要条件 B.必要不充分条件
C.既不充分又不必要条件 D.充要条件
2.设m,n是不同的直线,,是不同的平面,则下列命题正确的是( )
A.若,,,则 B.若,,,则
C.若,,,则 D.若,,,则
3.在正方体中,点O为线段BD的中点,设点P在直线上,直线OP与平面所成的角为,则的取值范围是( )
A. B. C. D.
4.在四面体ABCD中,为正三角形,AB与平面BCD不垂直,则下列说法正确的是( )
A.AB与CD可能垂直
B.A在平面BCD内的射影可能是B
C.AB与CD不可能垂直
D.平面ABC与平面BCD不可能垂直
5.已知矩形,,.将沿矩形的对角线BD所在的直线进行翻折,在翻折过程中( )
A.存在某个位置,使得直线AC与BD垂直
B.存在某个位置,使得直线AB与CD垂直
C.存在某个位置,使得直线AD与BC垂直
D.对任意位置,三对直线“AC与BD”“AB与CD”“AD与BC”均不垂直
6.成语“运筹帷幄之中,决胜千里之外”,意思是在小小的军帐之内作出正确的部署,决定了千里之外战场上的胜利,说的是运筹的重要性.“帷幄”是古代打仗必备的帐篷,又称“幄帐”,如图是一种幄帐示意图,帐顶采用“五脊四坡式”,四条斜脊的长度相等,一条正脊平行于底面.若各斜坡面与底面所成二面角的正切值均为,底面矩形的长与宽之比为,则正脊与斜脊长度的比值为( )
A. B. C. D.
7.如图,将正四棱柱斜立在平面上,顶点在平面内,平面,.点P在平面内,且.若将该正四棱柱绕旋转,则PC的最大值为( )
A. B. C. D.
8.已知二面角的平面角为,,,,,,AB与平面所成角为.记的面积为,的面积为,则的取值范围为( )
A. B. C. D.
二、多项选择题
9.如图,在四面体中,,,,O为AC的中点,点M是棱BC的中点,则( )
A.平面ABC
B.
C.四面体的体积为
D.异面直线PM与AB所成角的余弦值为
10.如图,在棱长为1的正方体中,E,F分别为棱,的中点,G为线段上一个动点,则( )
A.存在点G,使直线平面EFG
B.平面EFG截正方体所得截面的最大面积为
C.三棱锥的体积为定值
D.存在点G,使平面平面
11.如图,在正四棱锥中,E,M,N分别是BC,CD,SC的中点,动点P在线段MN上运动时,下列四个结论中恒成立的为( )
A. B. C.平面SBD D.平面SAC
12.正方体的棱长为2,M是正方形ABCD的中心,P为线段上一动点,则( )
A.
B.直线与直线AD所成角的余弦值为
C.不存在点P使得平面
D.三棱锥的体积为定值
三、填空题
13.已知三个互不重合的平面,,,且直线m,n不重合,由下列条件:①,;②,;③,,;能推得的条件是__________.
14.如图,在正方体中,点P在线段上运动,有下列判断:①平面平面;②平面;③异面直线与所成角的取值范围是;④三棱锥的体积不变.其中,正确的是__________(把所有正确判断的序号都填上).
15.刻画空间弯曲性是几何研究的重要内容,用“曲率”刻画空间弯曲性,规定:多面体顶点的曲率等于与多面体在该点的面角之和的差(多面体的面的内角叫做多面体的面角,角度用弧度制).例如,正四面体的每个顶点有个面角,每个面角为,所以正四面体在各顶点的曲率为.在底面为矩形的四棱锥中,底面ABCD,,PC与底面ABCD所成的角为,在四棱锥中,顶点的曲率为______.
16.在四棱锥中,底面ABCD是边长为的正方形,P在底面的射影为正方形的中心O,,Q点为AO中点.点T为该四棱锥表面上一个动点,满足PA、BD都平行于过QT的四棱锥的截面,则动点T的轨迹围成的多边形的面积为__________________.
四、解答题
17.如图,在四棱锥中,底面ABCD是矩形,PA为点P到平面ABCD的距离,,,,点E,M分别在线段AB,PC上,其中E是AB中点,,连接ME.
(1)当时,证明:直线平面PAD;
(2)当时,求三棱锥的体积.
18.如图1,在直角梯形ABCD中,,,,将沿AC折起(如图2).在图2所示的几何体中:
(1)若平面平面ABC,求证:;
(2)设P为BD的中点,记P到平面ACD的距离为,P到平面ABC的距离为,求证:为定值,并求出此定值.
19.在正方体中,M,N分别是线段,BD的中点.
(1)求证:平面;
(2)若正方体的棱长为2,求三棱锥的体积.
20.如图,在四棱锥中,底面ABCD是正方形,侧棱底面,.
(1)证明:平面平面PBD;
(2)点H在棱PC上,当二面角的余弦值为时,求.
参考答案
1.答案:B
解析:当,,时,直线a与直线b的位置关系是平行或者异面,故充分性不成立;当,,时,由直线与平面平行的判定定理,知,故必要性成立,所以“”是“”的必要不充分条件.
2.答案:D
解析:对于A,若,,,则直线m与n可能相交,也可能平行,还可能是异面直线,A错误;
对于B,若,则,B错误;
对于C,若,直线m与n可能平行,
如直线m,n都平行于,的交线,且,,满足条件,而,C错误;
对于D,若,,则,又,因此,D正确.
故选:D
3.答案:A
解析:由题意可得:直线OP于平面所成的角的取值范围:
不妨取 .
在中, .
的取值范围是 .
故答案为.
4.答案:A
解析:如图所示:取CD的中点E,连接AE,BE
假设,因为为等边三角形,所以,
又因为,所以平面ABE,所以
又因为E是CD中点,所以,只需满足,即可做到,故A正确C错误;
对于B:若A在平面BCD内的射影为B,则有平面BCD,与题干矛盾,故B错误;
对于D:过C点可以做出一条直线,使得该直线垂直与平面BCD,A点只需在该直线上,
即满足平面BCD即可达到要求,故D错误.
故选:A.
5.答案:C
解析:如图,作于点E,于点F.
因为,,所以,.
A项,若存在某个位置;使得直线AC与直线BD垂直,因为,连接,平面AEC,所以平面AEC,从而,这与已知矛盾,排除A;B项,若存在某个位置,使得直线AB与直线CD垂直,因为,平面ABC,所以平面ABC,因为平面BCD,所以平面平面BCD,取BC中点M,连接ME(图略),则,所以就是二面角的平面角,此角显然存在,即当A在底面BCD上的射影位于BC的中点时,直线AB与直线CD垂直,故B正确;C项,若存在某个位置,使得直线AD与直线BC垂直,因为,所以平面ACD,从而平面平面BCD,即A在底面BCD上的射影应位于线段CD上,这是不可能的,故排除C;D项,由以上所述,可排除D.故选B.
6.答案:B
解析:如图,多面体中,取AB的中点C,做交MN于Q,
做底面ABNM于E点,则E点在CQ上,且E点到BN,AM的距离相等,即,做于H点,连接EH,,则平面DHE,
所以,所以坡面与底面所成二面角为,又,则平面DCE,
所以,坡面与底面所成二面角为,
所以正切值,
不妨设,,
可得斜脊,因为矩形宽,
所以长为8,这样正脊,所以正脊与斜脊长度的比值为即.
故选:B.
7.答案:D
解析:过点C作,垂足为E,连接AC,可知平面,
所以点C到平面的距离为,
由题意,
,,
过点C作平面,垂足为,
因为点P在平面内,且,即点P在以为圆心,为半径的圆上,
当,,P三点共线时,且时,PC取最大值,
最大值为.
故选:D.
8.答案:C
解析:作,垂足为E,连接BE,
因为,即,,AE,平面AEB,
故平面AEB,平面AEB,故,
又,故平面,平面,
则AB在内的射影在BE上,则为AB与平面所成角,即,
由于,,故为二面角的平面角,即,
,
在中,,
则,
而,则,
则,,
故,
故选:C
9.答案:ABD
解析:对A:连结OB,
如图,在四面体中,,,,O为AC的中点,
所以,,且,.
所以,所以.
又因为,OB,平面ABC,所以平面ABC,故A正确;
对B、C、D:连接OM,由A知,平面ABC,平面ABC,所以,,
所以,故B正确;
因为AB与OM平行,所以OM与PM所成的角就是PM与AB所成角,在直角三角形POM中,,故D正确;
四面体的体积:,故C错误;
故选:ABD.
10.答案:AC
解析:对于A项,如图所示,
取中点H,I,连接HI交于G点,此时,
由正方体的性质知:面,又,则面,
面,可得,
在正方形中,易知,,面EFG,
所以平面EFG,故A正确;
对于B项,若G点靠C远,如图一示,过G作,即截面为四边形EFQR,
显然该截面在G为侧面CB1的中心时取得最大,最大值为,
若G靠C近时,如图二示,G作KJEF,延长EF交,DA延长线于M,H,
连接MK,HJ交,AB于L,I,则截面为六边形EFIJKL,
若K,J为中点时六边形面积为,,即B错误;
对于C项,随着G移动但G到面的距离始终不变即,
故是定值,即C正确;
对于D项,如图所示,连接,H为侧面的中心,则面与面和面分别交于线PG,DH,
若存在G点使平面平面,则,又,
则四边形PGHD为平行四边形,即,而,
此时G应在延长线上,故D错误;
故选:AC
11.答案:AC
解析:如图所示,连接AC,BD相交于点O,连接EM,EN,SO.由正四棱锥,可得底面,,所以.因为,所以平面SBD.
因为E,M,N分别是BC,CD,SC的中点,所以,,而,所以平面平面SBD,所以平面EMN,所以,故A正确;
由异面直线的定义可知,当P与M不重合时,EP与BD是异面直线,不可能有,因此B不正确;
平面平面SBD,所以平面SBD,因此C正确;平面SAC,若平面SAC,则,与相矛盾,因此当P与M不重合时,EP与平面SAC不垂直,即D不正确.故选AC.
12.答案:ABD
解析:对于选项A:在中,是的中点,故,正确;
对于选项B:设N是AB的中点,连接MN,则,
所以是异面直线与直线所成角(或其补角),
在中,,,,
所以,正确;
对于选项C:根据正方体的性质可知,,
由于平面,平面,所以平面,
同理可证得平面,
由于,BD,平面,所以平面平面,
当时,平面,所以平面,
即存在点P使得平面,错误;
对于选项D:,正确.
故选:ABD.
13.答案:②
解析:对于①,可能,所以①不成立;对于②,根据面面平行的性质可知,条件②能推出.对于③,可能,所以③不成立.所以能推得的条件是②.
故答案:②.
14.答案:①②④
解析:对于①,在正方体中,平面,平面,
平面平面,故①正确;
对于②,连接,如图:
容易证明平面//平面,
又平面,
平面故②正确;
对于③,,
异面直线与所成的角就是直线AP与所成的角,
在中,易知所求角的范围是,故③错误;
对于④,
点C到平面的距离不变,且的面积不变,
三棱锥的体积不变,故④正确.
综上所述,正确的是①②④.
故答案为:①②④.
15.答案:或
解析:
设,则,
平面ABCD,即为与底面ABCD所成角,即,
,,
,,;
平面ABCD,平面ABCD,,
又,,PA,平面PAB,平面PAB,
平面PAB,,即,又,
顶点的曲率为.
故答案为:.
16.答案:
解析:取AD的中点E,PD的中点F,PO的中点R,PB的中点N,
连接QR延长交PC与点M,依次连接E,F,M,N,G,
可知,,,即,而,
所以E,F,G,Q,N,R共面,所以E,F,M,N,G共面,
因为底面ABCD是边长为的正方形,
所以对角线,,
因为P在底面的射影为正方形的中心,可得面ABCD,
因为面ABCD,所以,
因为,,所以,
因为E、F分别为AD、PD的中点,
所以,且,
因为平面EFMG,平面EFMG,
所以平面EFMG,同理平面EFMG,
所以平面EFMG即为所求截面.
又因为平面平面,平面APC,所以,
因为Q为AO的中点,可得,
所以, ,,
因为N、F分别为PB、PD的中点,所以,,
所以,,所以四边形EFNG是平行四边形,
因为,,,所以平面APC,
因为平面APC,可得,所以,
所以四边形EFNG是矩形,
所以动点T的轨迹围成的多边形的面积为.
故答案为:.
17.答案:(1)证明见解析
(2)2
解析:(1)取PD中点N,连接MN,AN,
是的中位线,MN//CD,且,
又AE//CD,且,四边形AEMN为平行四边形,
又平面PAD,平面PAD,平面PAD.
(2),P到平面ABCD距离为3,
点M到平面ABCD的距离为1,
.
18.答案:(1)证明见解析
(2)证明见解析,2
解析:(1)记,在中,,,
在中,,由余弦定理得,
所以,所以,
因为平面平面ABC,平面平面,BC平面ABC,
所以平面ACD,又平面ACD,所以;
(2)由题意,,
因为P为BD的中点,,
所以,即.
19.答案:(1)证明见解析
(2)
解析:(1)连接,AN,如下图:
是线段BD的中点,底面ABCD是长方形,是线段AC的中点,
又是线段的中点,在中,,
平面,平面,平面.
(2)取BC的中点为O,连接MO,如下图:
,O分别是线段,BC的中点,在中,,,
又在正方体中,平面ABCD,平面ABCD,
为BD的中点,,
.
20.答案:(1)证明见解析
(2)
解析:(1)证明:如图,连接,侧棱底面,平面ABCD,.
又底面ABCD是正方形,.而且,,平面PBD,平面PBD.又平面,平面平面PBD.
(2)如图,过H作交DC于点E,过E作于点F,连接HF.
在平面PDC中,,,,底面ABCD,平面ABCD.
又平面,.
又,,,平面HEF,
平面HEF.又平面,,为二面角的平面角.故,则.
设,则,,.
在中,,.
在中,,
,当二面角的余弦值为时,.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
