浙教版数学八年级下册 期末检测卷(无答案)
文档属性
| 名称 | 浙教版数学八年级下册 期末检测卷(无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 920.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-09 08:30:44 | ||
图片预览

文档简介
期末检测卷
班级 学号 得分 姓名
一、选择题(本大题有10小题,每小题3分,共30分)
1.下列图标中,既是轴对称图形,又是中心对称图形的是( )
2.下列根式是最简二次根式的是( )
3. 已知关于x的一元二次方程. 有一个根为1,则k的值为( )
A. —2 B. 2 C. -4 D. 4
4.在“市长杯”足球比赛中,六支参赛球队进球数如下(单位:个):3,5,6,2,5,1,这组数据的众数是( )
A. 5 B. 6 C. 4 D. 2
5. 根据下面表格中的取值,方程. 有一个根的近似值(精确到0.1)为( )
x 1.2 1.3 1.4 1.5
x +x-3 —0.36 —0.01 0.36 0.75
A. 1.5 B. 1.2 C. 1.3 D. 1.4
6. 如图,在 ABCD中,∠BAD=120°,连接BD,作AE∥BD交CD 延长线于点E,过点 E作EF⊥BC交BC的延长线于点F,且CF=1,则AB的长是( )
A.2 B.1 C D
7. 一种药品原价每盒25元,经过连续两次降价后每盒16元.设平均每次降价的百分率为x,则x满足( )
A. 16(1+2x)=25 B. 25(1—2x)=16
8.用尺规在一个平行四边形内作菱形,下列作法中错误的是( )
9. 如图,矩形ABCD的边分别与两坐标轴平行,对角线AC经过坐标原点,点D 在反比例函数 (x>0)的图象上.若点B的坐标为(-4,-4),则k的值为( )
A. 2 B. 6 C. 2或3 D. -1或6
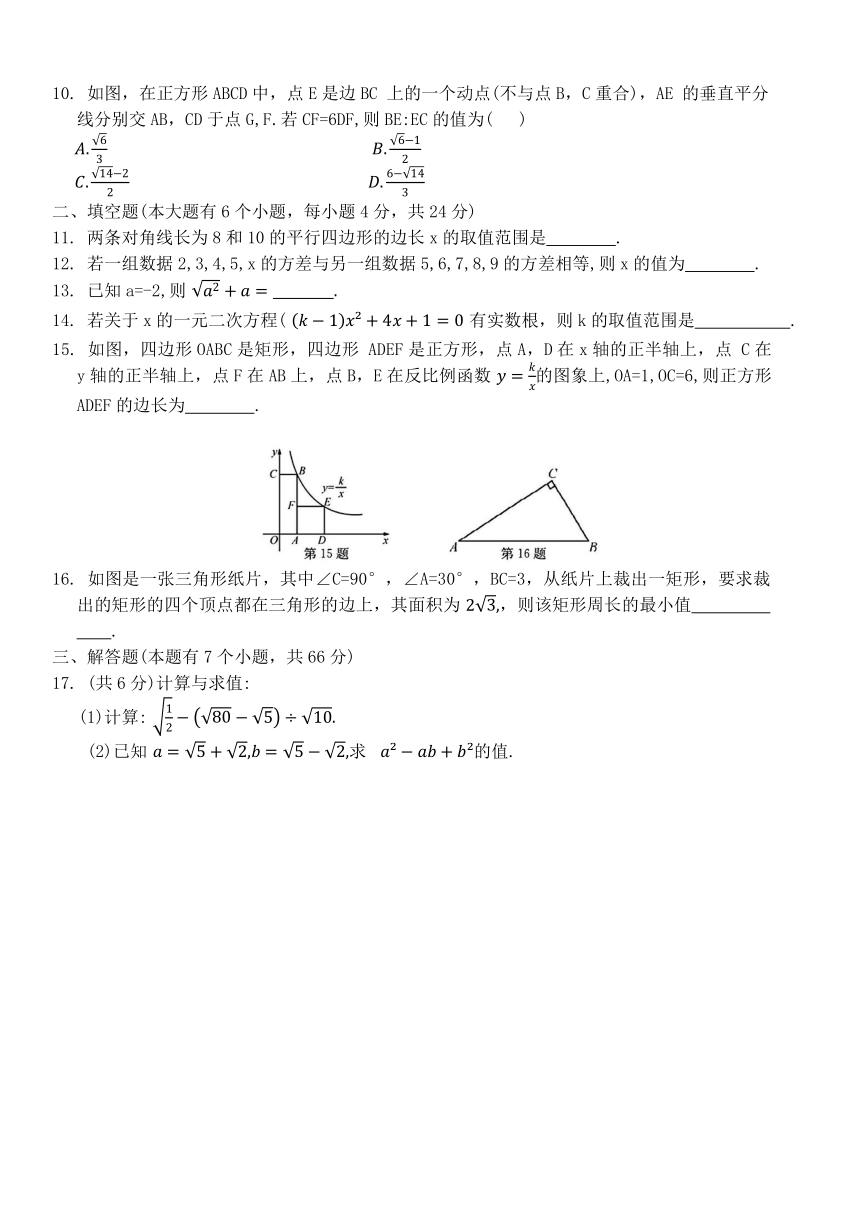
10. 如图,在正方形ABCD中,点E是边BC 上的一个动点(不与点B,C重合),AE 的垂直平分线分别交AB,CD于点G,F.若CF=6DF,则BE:EC的值为( )
二、填空题(本大题有6个小题,每小题4分,共24分)
11. 两条对角线长为8和10的平行四边形的边长x的取值范围是 .
12. 若一组数据2,3,4,5,x的方差与另一组数据5,6,7,8,9的方差相等,则x的值为 .
13. 已知a=-2,则
14. 若关于x的一元二次方程( 有实数根,则k的取值范围是 .
15. 如图,四边形OABC是矩形,四边形 ADEF是正方形,点A,D在x轴的正半轴上,点 C在y轴的正半轴上,点F在AB上,点B,E在反比例函数 的图象上,OA=1,OC=6,则正方形ADEF的边长为 .
16. 如图是一张三角形纸片,其中∠C=90°,∠A=30°,BC=3,从纸片上裁出一矩形,要求裁出的矩形的四个顶点都在三角形的边上,其面积为 ,则该矩形周长的最小值 .
三、解答题(本题有7个小题,共66分)
17. (共6分)计算与求值:
(1)计算:
(2)已知 求 的值.
18. (8分)解方程:
19.(8分)如图,已知在平行四边形ABCD 中,对角线AC与BD 相交于点E,点G为AD 的中点,连结CG,CG的延长线交 BA的延长线于点 F,连结 FD.
(1) 求证:
(2)若 ,判断四边形 ACDF的形状,并证明你的结论.
20. (10分)(8分)记面积为 的平行四边形的一条边长为 x(cm),这条边上的高线长为 y( cm).
(1)写出y关于x 的函数表达式及自变量x的取值范围.
(2)在如图直角坐标系中,用描点法画出所求函数的图象.
(3)若平行四边形的一边长为4 cm,一条对角线长为 请直接写出此平行四边形的周长.
21. (10分)某校七年级举行一分钟投篮比赛,要求每班选出10名学生参赛,在规定时间每人进球数不低于 8个为优秀,冠、亚军在甲、乙两班中产生,图①、图②分别是甲、乙两个班的10名学生比赛的数据统计图(单位:个).
根据以上信息,解答下列问题:
(1)将下面的“1分钟投篮测试成绩统计表”补充完整.
(2) 你认为冠军奖应发给哪个班 简要说明理由.
1分钟投篮测试成绩统计表
统计量 班级 平均数 中位数 方差 优秀率
甲班 6.5 3.45 30%
乙班 6 4.65
22. (12分)如图,在矩形ABCD中, ,过对角线BD中点O的直线分别交 AB,CD边于点E,F.
(1)求证:四边形BEDF是平行四边形.
(2)当四边形 BEDF 是菱形时,求 EF的长.
23.(12分)MO公司2022年使用自主研发生产的“QL”系列甲、乙、丙三类芯片共2800万块,生产了2800万部手机,其中乙类芯片的产量是甲类芯片的2倍,丙类芯片的产量比甲、乙两类芯片产量的和还多400万块.这些“QL”芯片解决了该公司2022年生产的全部手机所需芯片的10%.
(1)求2022年甲类芯片的产量.
(2)HW公司计划2024年生产的手机全部使用自主研发的“QL”系列芯片.从2023年起逐年扩大“QL”芯片的产量,2023年、2024年这两年,甲类芯片每年的产量都比前一年增长一个相同的百分数m%,乙类芯片的产量平均每年增长的百分数比m%小1,丙类芯片的产量每年按相同的数量递增.2022年到2024年,丙类芯片三年的总产量达到1.44亿块.这样,2024年的HW公司的手机产量比2022年全年的手机产量多10%,求丙类芯片 2024年的产量及m的值.
班级 学号 得分 姓名
一、选择题(本大题有10小题,每小题3分,共30分)
1.下列图标中,既是轴对称图形,又是中心对称图形的是( )
2.下列根式是最简二次根式的是( )
3. 已知关于x的一元二次方程. 有一个根为1,则k的值为( )
A. —2 B. 2 C. -4 D. 4
4.在“市长杯”足球比赛中,六支参赛球队进球数如下(单位:个):3,5,6,2,5,1,这组数据的众数是( )
A. 5 B. 6 C. 4 D. 2
5. 根据下面表格中的取值,方程. 有一个根的近似值(精确到0.1)为( )
x 1.2 1.3 1.4 1.5
x +x-3 —0.36 —0.01 0.36 0.75
A. 1.5 B. 1.2 C. 1.3 D. 1.4
6. 如图,在 ABCD中,∠BAD=120°,连接BD,作AE∥BD交CD 延长线于点E,过点 E作EF⊥BC交BC的延长线于点F,且CF=1,则AB的长是( )
A.2 B.1 C D
7. 一种药品原价每盒25元,经过连续两次降价后每盒16元.设平均每次降价的百分率为x,则x满足( )
A. 16(1+2x)=25 B. 25(1—2x)=16
8.用尺规在一个平行四边形内作菱形,下列作法中错误的是( )
9. 如图,矩形ABCD的边分别与两坐标轴平行,对角线AC经过坐标原点,点D 在反比例函数 (x>0)的图象上.若点B的坐标为(-4,-4),则k的值为( )
A. 2 B. 6 C. 2或3 D. -1或6
10. 如图,在正方形ABCD中,点E是边BC 上的一个动点(不与点B,C重合),AE 的垂直平分线分别交AB,CD于点G,F.若CF=6DF,则BE:EC的值为( )
二、填空题(本大题有6个小题,每小题4分,共24分)
11. 两条对角线长为8和10的平行四边形的边长x的取值范围是 .
12. 若一组数据2,3,4,5,x的方差与另一组数据5,6,7,8,9的方差相等,则x的值为 .
13. 已知a=-2,则
14. 若关于x的一元二次方程( 有实数根,则k的取值范围是 .
15. 如图,四边形OABC是矩形,四边形 ADEF是正方形,点A,D在x轴的正半轴上,点 C在y轴的正半轴上,点F在AB上,点B,E在反比例函数 的图象上,OA=1,OC=6,则正方形ADEF的边长为 .
16. 如图是一张三角形纸片,其中∠C=90°,∠A=30°,BC=3,从纸片上裁出一矩形,要求裁出的矩形的四个顶点都在三角形的边上,其面积为 ,则该矩形周长的最小值 .
三、解答题(本题有7个小题,共66分)
17. (共6分)计算与求值:
(1)计算:
(2)已知 求 的值.
18. (8分)解方程:
19.(8分)如图,已知在平行四边形ABCD 中,对角线AC与BD 相交于点E,点G为AD 的中点,连结CG,CG的延长线交 BA的延长线于点 F,连结 FD.
(1) 求证:
(2)若 ,判断四边形 ACDF的形状,并证明你的结论.
20. (10分)(8分)记面积为 的平行四边形的一条边长为 x(cm),这条边上的高线长为 y( cm).
(1)写出y关于x 的函数表达式及自变量x的取值范围.
(2)在如图直角坐标系中,用描点法画出所求函数的图象.
(3)若平行四边形的一边长为4 cm,一条对角线长为 请直接写出此平行四边形的周长.
21. (10分)某校七年级举行一分钟投篮比赛,要求每班选出10名学生参赛,在规定时间每人进球数不低于 8个为优秀,冠、亚军在甲、乙两班中产生,图①、图②分别是甲、乙两个班的10名学生比赛的数据统计图(单位:个).
根据以上信息,解答下列问题:
(1)将下面的“1分钟投篮测试成绩统计表”补充完整.
(2) 你认为冠军奖应发给哪个班 简要说明理由.
1分钟投篮测试成绩统计表
统计量 班级 平均数 中位数 方差 优秀率
甲班 6.5 3.45 30%
乙班 6 4.65
22. (12分)如图,在矩形ABCD中, ,过对角线BD中点O的直线分别交 AB,CD边于点E,F.
(1)求证:四边形BEDF是平行四边形.
(2)当四边形 BEDF 是菱形时,求 EF的长.
23.(12分)MO公司2022年使用自主研发生产的“QL”系列甲、乙、丙三类芯片共2800万块,生产了2800万部手机,其中乙类芯片的产量是甲类芯片的2倍,丙类芯片的产量比甲、乙两类芯片产量的和还多400万块.这些“QL”芯片解决了该公司2022年生产的全部手机所需芯片的10%.
(1)求2022年甲类芯片的产量.
(2)HW公司计划2024年生产的手机全部使用自主研发的“QL”系列芯片.从2023年起逐年扩大“QL”芯片的产量,2023年、2024年这两年,甲类芯片每年的产量都比前一年增长一个相同的百分数m%,乙类芯片的产量平均每年增长的百分数比m%小1,丙类芯片的产量每年按相同的数量递增.2022年到2024年,丙类芯片三年的总产量达到1.44亿块.这样,2024年的HW公司的手机产量比2022年全年的手机产量多10%,求丙类芯片 2024年的产量及m的值.
同课章节目录
